药代动力学(pharmacokinetics)简称药动学,从广义上讲,泛指研究药物的体内过程即机体对药物的吸收、分布、生物转化和排泄过程及其量变规律。狭义的药动学则是指以数学模型和公式,研究体内药物随时间的量变规律。本节主要介绍后者中与TDM有关的内容。在TDM工作中,药动学主要用于:①建立监测个体的体内药量或药物浓度随时间变化的数学表达式,并求算出有关药动学参数;②应用上述动力学模型、表达式和药动学参数,制定和调整个体化的用药方案,保证药物治疗的有效性和安全性。
一、药动学模型
药动学模型是为了定量研究药物体内过程的速度规律而建立的模拟数学模型。常用的有房室模型和消除动力学模型。
(一)房室模型
房室(compartment)是由具有相近的药物转运速率的器官、组织组合而成。同一房室内各部分的药物处于动态平衡。房室仅是按药物转运动力学特征划分的抽象模型,并不代表解剖或生理上的固定结构或成分。同一房室可由不同的器官、组织组成,而同一器官的不同结构或组织,可能分属不同的房室。此外,不同的药物,其房室模型及组成均可不同。运用房室模型,可将机体视做由一或多个房室组成的系统,从而将复杂的分布过程模型化。
若某药在体内各部位间均有较高及相近的转运速率,可在体内迅速达到分布平衡,则该药属单房室模型。属于单房室模型的药物,在体内达分布平衡后,其血药浓度将只受吸收和消除的影响。而某药在体内不同部位间转运速率存在较大差异的话,则将血液及其他血液供应丰富、并具有较高转运速率的部分,称做中央室,而把其余部分划归周边室,并可依次再分做第一周边室、第二周边室等,此即多室模型。根据划分的房室数,相应称为二室模型、三室模型等。属于多室模型的药物,其首先在中央室范围内达分布平衡,然后再和周边室间达到分布平衡,因此其血药浓度除受吸收和消除的影响外,在室间未达分布平衡前,还受分布的影响。
(二)消除动力学模型
消除动力学(eliminationkinetics)研究体内药物浓度变化速率的规律,可用下列微分方程表示:
dC/dt=-kCn
式中C为药物浓度,t为时间,k为消除速率常数,n代表消除动力学级数。当n=1时即为一级消除动力学,n=0时则为零级消除动力学。药物消除动力学模型即指这两种。
⒈一级消除动力学一级消除动力学(firstordereliminationkinetics)的表达式为:
dc/dt=-kC积分得Ct=C0e-kt
由上指数方程可知,一级消除动力学的最主要特点是药物浓度按恒定的比值减少,即恒比消除。有关一级消除动力学的其他性质及特点,将在本节二、三中详细讨论。
⒉零级消除动力学零级消除动力学(zeroordereliminationkinetics)时,由于n=0,因此其微分表达式为:
dc/dt=-k积分得Ct=C0-kt
由此可知,零级消除动力学的最基本特点为药物浓度按恒量衰减,即恒量消除。有关零级消除动力学的其它特点和性质,将在本节四中讨论。
必须指出,并不是某药固定按一级或零级动力学消除。任何药物当其在体内量较少,未达到机体最大消除能力时(主要是未超出催化生物转化的酶的饱和限时),都将按一级动力学方式消除;而当其量超过机体最大消除能力时,将只能按最大消除能力这一恒量进行消除,变为零级消除动力学方式,即出现消除动力学模型转换。苯妥英钠、阿司匹林、氨茶碱等常用药,在治疗血药浓度范围内就存在这种消除动力学模型转移,在TDM工作中尤应注意。
二、单室模型一级消除动力学
(一)单剂静脉注射
⒈模式图及药-时关系单室模型的药物可迅速在体内达到分布平衡,故可不考虑分布的影响。静脉注射用药时,药物直接迅速进入血液,因此也不受吸收的影响。此时体内药量将仅受包括生物转化和排泄在内的消除影响,可建立如下模式图。
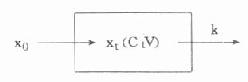
图9-2 单室模型单剂静脉注射模式图
图9-2中x0为剂量,xt为t时体内药量,Ct表示t时的血药浓度,V为表观分布容积,k为消除速率常数。当按一级动力学方式消除时,体内药量随时间变化的微分方程为:
dx/dt=-kX式⑴
积分得X=X0e-kt式⑵
因体内药量不可能直接测定,故引入比例常数:表观分布容积V,以便用血药浓度表示,即V=X/C,所以X=VC。代入式⑵可得
CC0e-kt式⑶
式⑶取对数得IgC=IgC0-kt/2.303式⑷
⑶和⑷式即为单室模型单剂静脉注射给药时的药-时关系表达式。
⒉药动学参数及计算
⑴药-时关系表达式:从式⑷可看出,当血药浓度以对数表示时,与时间t的关系为简单的直线关系。因此,在静脉注射药物后不同时间取血,测定血药浓度。根据血药浓度对数值及相应时间,以图解法或线性回归法(最小二乘方法),即可求得如式⑷的直线方程(图9-3)。
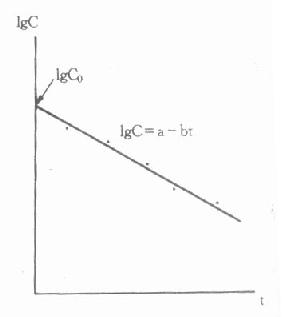
图9-3 单剂静脉注射血药
浓度-时间关系示意图
IgC=a-bt
此直线方程与纵轴的截距a=IgC0,故C0=Ig-1a;而斜率b=k/2.303,可计算出消除速率常数:
k=2.303b。
⑵消除速率常数:消除速率常数(eliminationrateconstant,k)表示单位时间内机体能消除药物的固定分数或百分比,单位为时间的倒数。如某药的k=0.2h-1,表示机体每小时可消除该小时起点时体内药量的20%,此即一级消除动力学的恒比消除特点。此时虽然单位时间消除的百分比不变,但随着时间的推移,体内药量逐渐减少,单位时间内消除的药量也逐渐减少,而不是恒定不变的,消除速率常数是反映体内药物消除快慢的一个重要参数。必须指出,一个药物的消除速率常数在不同的个体间存在差异,但对同一个体来说,若无明显的影响药物体内过程的生理化、病理性变化,则是恒定的,并与该药的剂型、给药途径、剂量(只要在一级动力学范围内)无关。
⑶半寿期:药动学中的半寿期(halflife,t1/2)通常是指血浆消除半寿期,即血浆中药物浓度下降一半所需要的时间。根据这一定义,当t=t1/2时,C0=2C,代入式⑷并整理可得
t1/2=0.693/k式⑸
从式⑸可看出,由于一级消除动力学时,k为一常数,半寿期亦为一常数。半寿期恒定不变,是一级消除动力学的又一特征。和消除速率常数一样,半寿期也是衡量药物消除快慢的又一临床常用参数,二者的关系如式⑸所表达。在药物的临床药动学参数资料中,常告知半寿期,只要知道半寿期,根据式⑸即可求得消除速率常数k值。半寿期在指导用药方案的制定中,有较大意义,将在后面讨论。
⑷表现分布容积:如前所述,表观分布容积(apparentvolumeofdistribution,V)是为了用血药浓度计算体内药量而引入的比例常数,表示假设体内药物按血药浓度均匀分布所需要的容积。前已谈到药物在体内分布可达动态平衡,但并非均匀一致,因此表观分布容积仅是一理论容积,并不代表真实的解剖或生理空间。但只要知道某药的表观分布容积V,应用测定的血药浓度,即可根据Xt=Ct·V,计算得实际工作中无法测定的任一时刻体内的药量,并可按上式计算出欲达某一血药浓度C所需使用的剂量X=CV。此外,表现分布容积还可用于评估药物在体内的分布特点。人的总体液量约0.6L/kg体重,若某药的V远远大于0.6L/kg体重,提示该药主要分布于细胞内,被某组织、脏器主动摄取或对某些组织成分有特殊亲和力,致使包括血浆在内的细胞外液中浓度低。大多数弱碱性药由于细胞内液比细胞外液偏酸而存在这一情况,如奎尼丁的表观分布容积可超出2L/kg体重。反之,若某药表观分布容积远远低于0.6L/kg体重,则其主要分布于血浆等细胞外液中。多数弱酸性药便是如此,如水杨酸的表观分布容积仅0.2L/kg体重。
单室模型静脉注射用药时V的求算可采用外推法,即根据前面介绍的药-时关系表达式求得t=0时的C0值及注射剂量X0,按V=X0/C0而计算出。其单位最常采用容积单位/kg体重。同前述药动学参数一样,V也是仅取决于药物本身的理化性质、体内分布特点,而与该药剂型、用药方式、并在一级消除动力学范围内与剂量都无关。在所有药动学参数中,V和k是两个最基本的参数。
⑸清除率:药物清除率(clearance,Cl)是指单位时间内机体从血浆中消除某种药物的总能力,其数值即等于该时间内机体能将多少体积血浆中的该药完全消除。与k和t1/2相同,Cl也是衡量体内药物消除快慢的一个药动学参数,但与k和t1/2不同,Cl以具体的解剖生理学概念来表示,可更直观形象地反映机体对药物的消除能力。由于药物在体内按血浆浓度分布的总体积为V,而k表示单位时间内药物被消除的分数,故代表单位时间内机体能消除多少体积血浆药物的清除率可按Cl=Vk计算,单位为体积单位/时间单位。
⑹曲线下面积:血药浓度-时间曲线与纵轴和横轴间围成的范围面积即曲线下面积(areaundertheC-tcurve,AUC),单位为浓度单位×时间单位。由于任何药物不论以何种剂型或途径用药,进入体内后,只要是同一种药物分子,其消除均相同。因此AUC是评估进入体内药量多少的一个客观指标。在后面介绍的生物利用度的计算,以及近年建立的非模式消除动力学分析矩量法(statisticalmomenttheory)中,均有重要意义。
AUC的计算方法有称重法、梯形法和积分法3种。其中称重法为剪下曲线下纸片称取重量,除以单位面积纸片的重量,即为该曲线的AUC。该法较不准确,现已少用。下面介绍后两种计算方法。
1)梯形法:如图9-4所示,可将曲线下范围分做若干个等高梯形,分别计算各个梯形面积累加而成。即:

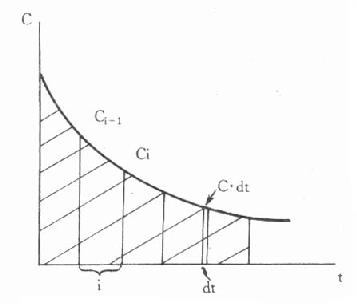
图9-4 单剂静脉注射时的药-时曲线下面积
此法不论何种房室模型及何种途径给药均适用。但本法只能求算测定血药浓度的时间范围内的AUC。
2)积分法:当药-时曲线按足够小的时间间隔dt划分时,可视做若干个矩形,每个矩形的面积分别为C·dt,将其积分得:

药动学中积分法求算的AUC,均表示曲线随时间无限外延,直至体内药量完全消除时的面积。此外式⑺仅适用于单室模型、一级消除动力学单剂静脉注射给药的情况。
(二)恒速静脉滴注
恒速静脉滴注用药,是临床特别是危重症抢救中常用的方法。此时通过TDM工作,制定和调整滴注药物速度,对确保抢救效果有重要意义。
⒈模式图和药-时关系表达式恒速静脉滴注与单剂静脉注射不同,此时药物一方面以恒速的零级动力学方式进入体内,另一方面又以恒比的一级动力学方式从体内消除(图9-5)。
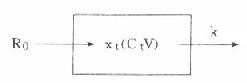
图9-5 单室模型恒速静脉滴注模式图
图中R0为滴注速度,R0=X0/t0,X0为t0时间内滴注入体内的总药量。余参数意义同图9-2。此时体内药量随时间变化的微分表达式为:
dx/dt=R0-kX积分得X=R0/k(l-e-kt)式⑻
或C=R0/Vk(l-e-kt)式⑼
式⑻、⑼即为恒速静脉滴注、单室模型一级消除动力学的体内药量或血药浓度随时间变化的基本表达式。
⒉药动学参数及计算
⑴稳态血药浓度:稳态血药浓度(steadystateplasmaconcentration,Css)指单位时间内自体内消除的药量与进入体内的药量相等时的血药浓度。此时,血药浓度将维持在坪值或波动在一定范围内(多剂分次给药时)。恒速静脉滴注时,只要滴注速度R0能使体内药量保持在一级动力学消除范围内,则当t→∞时,式⑼中e-kt→0,式⑼可写作
Css=R0/(k·V)式⑽
从式⑽可看出,由于k、V都是常数,恒速滴注时,R0也不变,故此时血药浓度亦为一常量,即达到稳态浓度。并且从式⑽还可看出,Css高低仅与R0成正比。这也是只要滴注速度得当,长期静脉恒速滴注,血药浓度不会无限上升产生毒性反应的原因。此外,知道某药的k、V值及达到治疗作用所需的Css后,则可根据式⑽计算出所需的滴注速度R0=Css·k·V,需指出的是,当恒速静脉滴注药物用于抢救心衰或休克病人时,随着血流动力学的改善,病人的k及V均可改变,必须通过TDM及时调整滴注速度,以保持在所需的Css。
若将时间用半寿期数n表示,即t=nt1/2=0.693n/k,应用前面学过的公式,可得到达稳态前血药浓度C与Css的关系:
C=Css[1-(1/2)n]式⑾
从式⑾可计算出恒速静脉滴注经过5个半寿期,血药浓度可达Css的96.8%,6个半寿期达98.4%。因此,临床上通常视恒速静脉滴注经过5-6个半寿期后,达到了稳态血药浓度。
⑵静脉滴注的负荷剂量:从上可知,为达Css,至少需恒速静脉滴注5-6个半寿期以上。而临床抢救中常需迅速达到有效血药浓度,此时可考虑使用负荷剂量法。负荷剂量(loadingdose,D)是为了迅速或立即达到稳态浓度而首先使用的增大剂量。静脉滴注用药时,有下面两种负荷剂量法。
1)先静脉注射一负荷剂量,立即达Css,继之以恒速滴注维持。根据前面所学知识可得D=Css·V=R0/k。故根据治疗浓度确定的所需Css和该药的V,或为达所需Css计算出的恒速滴注速度R0和该药的k,即可按上式求得所需D,静脉推注后,立即改为R0速度恒速滴注,便可立即达到Css并维持之。
2)先快速滴注t时间,迅速达所需Css水平,再改为恒定的慢速滴注维持。此法较上法安全,尤适用于毒性大、治疗浓度与中毒浓度接近的药物。此时可根据下式(推导从略)计算出所需的负荷速度R0*:
R0*=R0/l-e-kt式⑿
式中R0为达所需Css计算出的恒定慢速滴注速度,t为计划的负荷滴注时间。按R0*滴注t时间后,血药浓度即可迅速升至Css水平,调整滴注速度为R0,即可维持在Css水平。
⑶其它药动学参数计算:若已知某药其它方式用药时的有关药动学参数,前已述及也可用于恒速静脉滴注。当需通过恒速静脉滴注计算药动学参数,可使用终止滴定法。即在恒速静脉滴注t时间后,停止滴注,以t时间为零时,测定随后几个不同的时点(t’)的血药浓度,同前静脉注射法求得直线方程:
IgCt=
应注意此式的t为开始滴注到停止滴注的时间。然后根据下列各式:
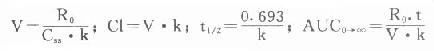
分别计算出各有关药动学参数。
(三)血管外单剂用药
⒈模式图和药-时关系表达式口服、肌肉或皮下注射用药时,和前面讨论的血管内给药不同。此时即存在药物从用药部位吸收进入血液的过程,也存在药物自体内(血液)消除的影响。由于绝大多数药物均是以被动转运的方式吸收,故上述两个过程都按一级动力学方式进行。其模式图如下(图9-6):
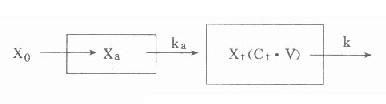
Xa:t时吸收部位药量
Ka:吸收速率常数其它参数同图9-3
图9-6 血管外用药模式图
根据上述关系及模式图,可建立如下微分方程组:
dxa/dt=-Ka·Xa(吸收部位药物衰减速率)
dxa/dt=-Ka·Xa--K·X(血液等药物分布室内药物衰减速率)
解此微分方程组得
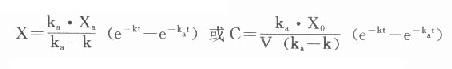
若考虑口服时吸收不完全而引入吸收分数F,则:

式⒀即为单剂血管外用药时,血管浓度随时间变化的基本表达式。
⒉药动学参数及计算通过血管外用药计算药动学参数多用残数法(methodofresidual)。该法基本指导思想是,以血管外用药能获治作用的药物,必然Ka>>k,才有可能在体内达到治疗血药浓度,因此,当t足够大时,首先e-kat→0此时式⒀可写作:
C=A·e-kt取对数得lgC=lgA-kt/2.303
也就是说单剂血管外用药时,经过一段时间后,其血药浓度的变化可视做只受消除的影响,即进入消除相(图9-7)。
此时按前面介绍的单剂静脉注射药动学参数计算法,可求得A、k和消除t1/2。而在进入消除相以前的时间内,血药浓度为吸收和消除两因素共同作用的结果。若将式⒀展开移项则得
A·e-kt-C=A·e-kat,令Cr=A·e-kt-C,

图9-7 单剂血管外用药血药
浓度-时间关系及药动力学求算示意图
Cr为消除相外推段某时点血药浓度减去该时点实测浓度的残数或差值(注意不是对数值相减)。则:
Cr=A·e-kat,取对数得TgCr=IgA-kat/2.303
此即分布相药-时关系的表达式(图9-6),同理可求算得ka和吸收t1/2。
在计算其它药动学参数时,反映药物被机体吸收利用程度的吸收分数F,即生物利用度(bioavailability)是必须首先先知道的。血管外注射用药时,一般均视为F=1。而现在多数口服药在说明书中已告知F值,否则需根据某药口服时AUC与该药同剂量静脉注射时的AUC相比计算出。口服时的AUC可用前述梯形法,或按下列积分法公式求得:
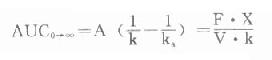
其他药动学参数计算见下。
⑴表观分布容积: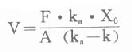
⑵清除率:Cl=k·V
⑶达峰时间(timeofthepeakconcentration,tp):即血管外给药时,达到最高浓度所需时间。由于在此时,血药浓度变化速率dC/dt=0,故可推导出:
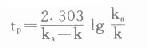
⑷峰浓度(maximumconcentration,Cmax):将tp代入式⒀可得:
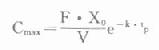
(四)多次用药
为保持或巩固疗效,临床常需反复多次较长期用药。此时体内药量或血药浓度将出现如图9-8所示的波动式上升,每次用药间隔中出现从峰值向谷值的变化。若体内药量不超过一级消除动力学范围,随着用药次数增多,血药浓度逐渐升高,但最终将稳定在一定范围内波动,即进入稳态浓度(推导见后)。指导合理的多次用药方案的制定和调整,使稳态血药浓度波动在治疗浓度范围内,是TDM在临床治疗学中最主要的任务。下面我们将介绍按恒定剂量、固定间隔时间多次用药时与TDM有关的药动学知识。需要指出的是,单剂用药时的有关药动学参数仍适用于多剂给药,并且是多剂用药药动学的基础。
⒈多剂量函数当按恒量固定间隔时间τ多次用药,无论是静脉注射,还是肌肉注射、口服等血管外用药,均可推导得多剂量函数r(推导从略)。
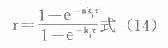
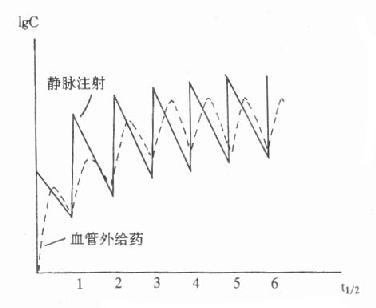
图9-8 多剂用药的血药浓度-时间关系示意图
n:用药次数
Ki:有关速率常数
多剂量函数为多剂用药时,用药间隔时间τ和用药次数n对体内药量或血药浓度的影响的通用函数表达式。具体应用时,只需将单剂用药有关公式中含有速率常数的指数或对数项乘以多剂量函数r即可。但要注意:①此时多剂量函数r中的ki均应换成该项之k或ka;②对数项时,多剂量函数r应放在对数内与有关速率常数相乘;③相应各公式中t应为第n次用药后的时间。如此根据⑶式可得多剂静脉注射用药时,药-时关系表达式为:
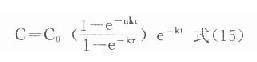
同理根据式⒀可得血管外多剂用药的药-时关系表达式为:
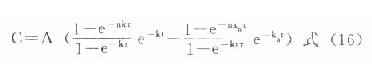
恒速静脉滴注时=0,仍用原式

⒉稳态浓度和平均稳态浓度当连续多次给药后,n足够大时,多剂量函数式中,则

显然此时的多剂量函数式为一常量,此即稳态时的多剂量函数式。分别代入式⒂或⒃中可得:
静脉注射时:
血管外给药时: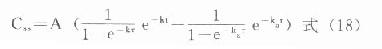
以上两式中,由于仅时间t在每次用药间隔中从0→τ的范围变化,血药浓度都将进入在每次用药间隔中,恒定在一定范围内波动的稳态状态。τ越大,波动范围越大。式⒄、⒅则分别为静脉注射、血管外用药时,稳态浓度在每次用药间隔中随时间变化的表达式。实际工作中,当nτ=6t1/2时,血药浓度可达稳态浓度的98.4%。故在连续多剂用药时,一般认为经过6个半寿期以上,即可视做已达稳态状态。此外,无论达稳态否,如果变换剂量,必须再经过6个半寿期以上始能进入新的稳态。
静脉注射时,每次间隔中波动的峰值总是在每次注射完的瞬间(t=0),而谷值则在下次注射前(t=τ)出现,分别代入⒄式可得静脉注射多剂用药时
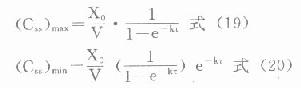
血管外给药时,每次间隔中,谷浓度也将在下次给药前。但由于存在吸收,峰浓度将在达峰时间(t’p)出现。将稳态时多剂量函数代入前述单剂用药tp,求算公式得:

分别以上述t’p或t=τ代入⒅式,并且因ka较大,令e-kaτ→0,可推得血管外给药的

在TDM工作中,运用式⒆-(22)式,选定间隔时间(τ),计算剂量,或选定剂量计算nt-family:TimesNewRoman;mso-fareast-font-family:宋体;mso-font-kerning:1.0pt;mso-ansi-language:EN-US;mso-fareast-language:ZH-CN;mso-bidi-language:AR-SA"lang="EN-US">τ,使(Css)max<最小中毒浓度,而(Css)min>最小有效浓度,是十分有用且经常性的工作。
平均稳态血药浓度( )为稳态时,两剂用药间药-时曲线下面积(AUC)除以间隔时间τ的商值。必须注意,(
)为稳态时,两剂用药间药-时曲线下面积(AUC)除以间隔时间τ的商值。必须注意,( )不是(Css)max和(Css)min的算术或几何平均值。根据稳态浓度的定义可知,此时两剂间AUC就为该剂量单剂给药时的AUC0→∞。根据前面学过的公式,可得
)不是(Css)max和(Css)min的算术或几何平均值。根据稳态浓度的定义可知,此时两剂间AUC就为该剂量单剂给药时的AUC0→∞。根据前面学过的公式,可得
静脉注射: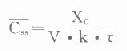
血管外用药:
在TDM工作中,对给药间隔τ不是远远长于半寿期,即稳态时血药浓度波动范围不是太大,且有效血药浓度范围上限与最小中毒浓度有一定差距的药物,以有效血药浓度范围中值或略低定为 ,按上式公式制定或调整用药方案,是一简便并且为临床所能接受的方法。
,按上式公式制定或调整用药方案,是一简便并且为临床所能接受的方法。
⒊负荷剂量上面讨论中谈到,多剂用药时,无论间隔时间长短,都需经过6个以上半寿期才可认为已达稳态。对t1/2较长或急需迅速发挥疗效的药物,往往需要使用负荷剂量(X0*)。多剂用药时欲使第一次用药后即达到稳态浓度,负荷剂量可按下面公式计算(推导从略)。
静脉注射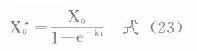
血管外用药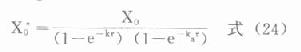
式中X0为拟使用的固定剂量。若吸收较快,即ka大,e-kaτ→0,(24)式也可写做

上述各式中1/(1-e-kτ)即前述稳态时的多剂函数式,亦称蓄积指数(accumulationindex),代表稳态时血药浓度峰值或谷值与首剂用药时峰值或谷值之比。蓄积指数实际上反映了达稳态后,每次给药间隔中任一时点血药浓度为首剂用药后同一时点血药浓度的倍数。如τ=t1/2时,蓄积指数为2,X0*=2X0。实际工作中,根据所需稳态血药浓度水平确定的X0及τ,按上述公式计算出负荷剂量X0*首剂使用后,再按X0及τ,恒量固定间隔用药,可在负荷剂量使用后即达稳态浓度并维持之,获得迅速而稳定的疗效。
三、二室模型一级消除动力学
多室模型和前面讨论的单室模型不同,此时存在着由包括血液在内的中央室向周边室分布达到平衡的过程,影响血药浓度的因素更为复杂,下面以单剂静脉注射为例,简介有关药动学知识。
(一)模式图和药-时关系
静脉注射时,不存在吸收过程,中央室中的药量或血药浓度受中央室与周边室间双向分布,以及自中央室消除的影响。其模式如图9-9所示。
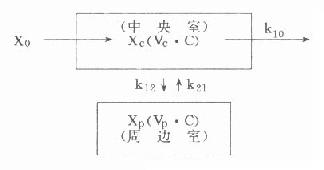
xc中央室药量
xp周边室药量
vc中央室分布容积
vp周边室分布容积
k10中央室向周边室转运速率常数
k21周边室向中央室转运速率常数
图9-9 二室分布静脉注射模式图
中央室药量变化的速率微分方程为:
dkc/dt=k21·xp-k21·xc-k10·xc
对上式积分并引入中央室分布容积Vc,可得中央室(血)药物浓度随时间变化的基本表达式:
C=A·e+B·e-βt式(25)
式中α为分布速率常数,β为消除速率常数,A、B为经验常数。四者都是由模式参数k10、k12、k21组成的混杂参数(hybridparameters)。存在:
α·β=k21·k10α+β=k10+k12+k21

(二)药动学参数计算
二室模型静脉注射药动学参数的求算,类似于单室模型血管外用药,仍采用残数法。即因为α>β,当t充分大时,A·e-αt→0,则式(25)变为
C=Be-βt
此即消除相药-时关系表达式。按前述方法可求得B、β和消除半寿期t1/2β。将式(25)移项可得:
C-B·e-αt=A·e-αt
令Cr=C-B·e-βt,Cr即为消除相以前某时点实测血药浓度减去消除相该点外推浓度的残数。代入上式可得分布相药-时关系表达式
Cr=A·e-αt
同样可求得A、α和分布半寿期t1/2α(图9-10)。

图9-10 二室模型静脉注射血药浓度-时间关系示意图
再根据下列公式,可求得各有关药动学参数。
中央室表观分布容积:Vc=X0/(A+B)
周边室向中央室的转运速率常数:
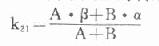
自中央室消除的速率常数:
k10=α·β/k21
中央室向周边室转运的速率常数:
k12=(α+β)-(k10+k21)
曲线下面积:AUC0→∞=A/α+B/β(积分外推法)
周边室表观分布容积:Vp=Vc·k12/k21
总表观分布容积: 表示体内药量按消除相血药浓度分布的容积)
表示体内药量按消除相血药浓度分布的容积)
稳态表观分布容积:Vss=Vc+Vp
消除率:Cl=k10·Vc=β·V
血管外用药时,由于存在吸收因素,求算药动学参数的基本方法仍为残数法,但此时需进行两次残数处理。有关二室模型血管外用药及二室以上多室模型的药动学,在TDM的实际工作中很少应用,可参阅有关药动学专著。
四、非线性动力学
在消除动力学模型中已介绍,当体内药量(血药浓度)超过机体最大消除能力时,将为恒量消除的零级动力学,而药量(血药浓度)降至最大消除能力以下,将转化为恒比消除的一级动力学(图9-11)。这种存在动力学转换的情况下,药物的消除不能用一种统一简单的线性过程描述,故称非线性动力学(nonlinearpharmacokinetics)消除。若某药使用的剂量能使其在体内的消除由一级动力学转为零级,继续使用该剂量,血药浓度将会出现持续上升,而不能达到稳态浓度。对于安全范围狭窄的药物出现这种情况,是十分危险的。在需进行TDM的药物中,苯妥英钠、氨茶碱等在常用治疗剂量下就存在这种情况。
造成这种药动学方式转化的原因,主要是体内药量(血药浓度)超过了机体生物转化酶系的最大催化能力,即出现了饱和代谢,故亦常用描述酶促反应动力学的米氏方程表达非线性动力学消除的速率,即
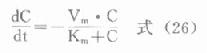
式中Vm为最大消除速率,Km为米氏常数,相当于恰可产生Vm/2时的药物浓度。当C<
dc/dt=VmKm,令0k=Vmdc/kmdt,则dc/dt=-kC
此即前面已介绍的典型一级消除动力学微分表达式。而当C>>Km时,式(26)可写作
dC/dt=-Vm
上式为典型的零级消除动力学微分表达式。
由式(26)可推导得非线性动力学消除时的有关药动学参数计算公式:


图9-11 非线性动力学消除血药浓度-时间关系示意图
从上述各式中可看出,非线性消除动力学药物的多数参数均为随药物浓度而变化的变量,并非常数。在非线性动力学消除的药物TDM工作中,Vm和Km是两个十分有用的基本常数。必须注意的是,在药物体内过程中,生物转化能力影响因素多,个体差异尤为显著,因此Vm和Km个体差异大。在应用这两个参数的群体均值制定的剂量方案,往往不能达到预期效果。对于需长期用药或完全范围窄的药物,按下面方法确定具体个体的Vm和Km值实属必要。
不同时点取血测定血药浓度,依次求得相邻时点血药浓度及时间差值△C和△t。将式(26)中的dC/dt视做△C/△t,即消除速率V,而以相应两时点血药浓度均值C作为产生相应速率改变的浓度,分别代入式(26),并取倒数整理得:
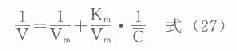
式(27)为1/V随1/C变化的直线方程(图9-12)。该直线与纵轴交点为1/Vm,斜率为Vm/Km,故可分别求出Vm和Km。

图9-12 双倒数法求算非线性动力学消除的Vm和Km示意图
根据非线性动力学消除的特点,多剂用药时,只有当药物进入体内的速率R(量/d)恰与药物自体内的消除速率相等时,才有可能达稳态浓度Css。借用式(26)可得
R=Vm·Cm/Km+Cm式(28)
由此可得Css=Km·R/Vm-R式(29)
由上两式可计算出非线性动力学消除的药物,欲达某稳态浓度所需的用药速率(每日用药量),或按某速率用药时所能达到的稳态浓度,在这类药物的TDM工作中极为有用。从式(28)、(29)中也可看出,Vm和Km是必须首先求算出的基础。
, http://www.100md.com