血液表观粘度乘幂表示及红细胞压积影响的消除
作者：尹志勇 王正国 蔡绍皙
单位：尹志勇 王正国 第三军医大学附属大坪医院野战外科研究所第四研究室 重庆，400042；蔡绍皙 重庆大学生物工程研究院 重庆，400044
关键词：表观粘度；乘幂函数；红细胞压积
提要 目的
提要 目的：寻找一种更为简洁有效的描述血液表观粘度的方法。方法：8例正常人和26例肺癌患者及4组用正常人自体血浆配制的不同压积血标本，首先测其表观粘度，然后用曲线拟合的方法筛选拟合方式，并对筛选出的乘幂法进行验证。结果：乘幂函数表示有利于消除血液粘度测量过程中的随机误差，红细胞压积与乘幂系数之间是一线性关系，提出了一种新的、更有效的消除红细胞压积影响的方法。结论：采用乘幂函数描述血液表观粘度是可行有效的方法。
中图法分类号 R331.1
, 百拇医药
Description of blood apparent viscosity with power function and a new method of eliminating hematocrit's interference
Yin Zhiyong, Cai Shaoxi, Wang Zhengguo
(Research Institute of Field Surgery, Daping Hospital, Third Military Medical University, Chongqing, 400042)
Abstract Objective: To seek a more laconic and effective method to describe the blood apparent viscosity. Methods: The blood samples from 8 healthy adults and 26 patients with lung cancer and 4 groups of blood samples with different hematocrits were used to obtain the apparent viscosity data. A power function was selected by curve coincidencing and validated by the apparent viscosity data. Results: The power function method was in favor of eliminating random errors in the process of measurement. The relationship between hematocrit and the coefficients of the power function was linear. Conclusion: The power function is a feasible and effective method to describe the blood apparent viscosity.
, 百拇医药
Key words apparent viscosity; power function; hematocrit
血液表观粘度是临床上常用的流变学指标，应用日益广泛[1，2]，但存在两个主要问题：一是表达形式不够理想，其次是采用还原粘度法比较不同红细胞压积下血液的流变特性时，误差较大。能否用更为简单、精确的方式表达血液表观粘度，并引入一种比还原粘度法更为有效地消除红细胞压积影响的新方法。
1 材料与方法
采取8例正常人、26例肺癌患者肝素抗凝的新鲜静脉血，并将部分取自正常献血者的红细胞分离后，用自身血浆配制成4组红细胞压积(Ht)分别为26.7%，36.0%,50.0%,66.7%的样本(每组8个样本)，分别按下法测定各样本的表观粘度。将约0.8 ml血标本注入Low Shear 30流变测定仪的Coutte氏小室中，小室内温度保持在37.0℃±0.1℃，分别在0.138, 0.187, 0.255, 0.346, 0.471, 0.639, 0.87, 1.182, 1.607, 2.19, 2.97, 4.04, 5.49, 7.46, 10.16, 13.79, 18.74, 25.5切变率处测试其表观粘度。对测得的表观粘度数据采用直线、对数、多项式、乘幂、指数、移动平均等方式进行拟合，筛选最佳拟合方式。
, http://www.100md.com
在血液表观粘度的测试过程中由于主观和客观原因会导致一些随机误差，我们在偶然的情况下观察到乘幂表示法对减少随机误差有效。为说明这一现象，采用以下方法进行分析。
随机抽取一正常人全血表观粘度数据，在其测试结果中人为加入最大值为±10%的随机误差，其计算公式为：
ηa′=ηa+(RAND()-0.5)×ηa÷5
(1)
式中ηa′为加入随机误差后的表观粘度值，ηa为原测试值，RAND()为大于等于0而又小于1的随机数。采用(1)式分别计算不同切变率处的表观粘度值并重复20次，记录每次实验数据，进行回归分析，求出系数a、b和R2，并分别计算各自的均值、标准差和标准差与均值之比。
, 百拇医药
为消除红细胞压积的影响，根据红细胞压积与乘幂系数的线性关系提出了一种新的消除红细胞压积的方法，步骤如下：
①根据测得的表观粘度数据采用回归分析计算出乘幂系数a,b。
②按下式计算a1和b1：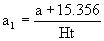
b1=b/Ht
(2)
③计算压积为45%处的乘幂系数a′和b′：
a′=a1×0.45-15.356
, http://www.100md.com
b′=b1×0.45
(3)
④同时也可计算压积为45%时各种切变率下的表观粘度值：
ηb′=a′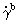
(4)
2 结果
在上述多种曲线拟合方式中，乘幂函数与血液表观粘度数据吻合得最好，即表观粘度可以用乘幂函数表示：
ηa=a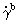
, http://www.100md.com
(5)
根据测得的表观粘度数据用回归分析可计算出每一例全血标本的表观粘度所对应的乘幂系数a、b和表征拟合程度的R2，其结果见表1。所有拟合曲线的R2都非常接近于1，因此，无论是正常人、肺癌患者，还是不同压积的血标本采用乘幂函数描述其粘度数据都是非常合适的。
表1 血液表观粘度乘幂函数系数
Tab 1 The coefficients of the power function of the blood apparent viscosity
Group
n
a
b
, 百拇医药
R2
Healthy adults
8
20.78±3.82
0.37±0.04
0.99±0.01
Lung cancer
26
20.25±7.04
0.38±0.06
0.99±0.01
Different Ht
, 百拇医药
26.7%
8
6.97±1.70
0.24±0.02
0.97±0.02
36.0%
8
10.2±2.12
0.31±0.03
0.97±0.02
50.0%
8
, http://www.100md.com 20.9±2.39
0.43±0.03
0.99±0.01
66.7%
8
34.7±3.07
0.53±0.02
0.99±0.01
在一正常人血表观粘度的测试结果中加入最大值为±10%的随机误差后，采用传统的高中低三点表示法和乘幂数表示法所得数据的统计结果见表2。
表2 加入随机误差后的表观粘度及对应的乘幂函数系数
, 百拇医药
Tab 2 The apparent viscosity and the coefficients of the power function after adding random error
Three points method
Coefficients of the power funtion
0.138(Low)
2.19(Medium)
25.5(High)
a
b
R2
, http://www.100md.com
Average(x)
62.052
21.027
8.378
29.512
0.420
0.989
Standard deviation(s)
14.147
4.362
3.853
0.390
, 百拇医药
0.007
0.003
CV(s/x)
0.228
0.207
0.460
0.013
0.016
0.003
可见采用三点法受随机误差的影响较大，其标准差与均值之比均大于20%。采用乘幂函数表示后，其比值小于2%，因此采用乘幂函数表示有利于降低随机误差的影响。
将表1中不同压积血标本的乘幂函数系数以散点图的形式表示在图1中，可见其散点图基本上分布在一条直线上，经回归分析可得乘幂函数系数与红细胞压积的回归方程：
, http://www.100md.com
a=a1H-a0=73.991H-15.356
b=b1H=0.8442H
(6)
图1 正常人红细胞压积与表观粘度乘幂函数系数的关系
Fig 1 The relationship between hematocrit of healthy adults and the coefficients of the power function
可见红细胞压积与乘幂系数之间的关系均为线性关系。
, 百拇医药
计算正常组和肺癌组在各切变率处表观粘度的均值和标准差，两组血液表观粘度比较除在切变率为25.5处P<0.05外，其余各点的差异不显著(P均>0.05)，而两组红细胞压积比较差异十分显著。根据实验数据分别计算出正常组和肺癌组乘幂系数a和b，然后按式(2)计算与红细胞压积无关的系数a1和b1，再按式(3)计算红细胞压积为45%时的乘幂系数a′和b′，其结果见表3。
表3 正常组和肺癌组乘幂系数及消除红细胞压积后的系数比较
Tab 3 The comparison of the coefficients of the power function
a
b
a1
, http://www.100md.com
b1
a′(45%)
b′(45%)
Healthy adults
20.779±3.820
0.368±0.040
80.354±5.793
0.819±0.077
30.803±2.607
0.369±0.034
Lung cancer
, http://www.100md.com
20.249±7.037
0.379±0.060
93.461±20.77
0.997±0.199
26.701±9.348
0.449±0.090
T test
0.430469
0.211893
0.00388
0.000435
, http://www.100md.com 0.00388
0.000435
正常组和肺癌组的系数a和b的差异不显著(P<0.05)，这与直接采用表观粘度值分析得出的结论一致，二者都没有消除红细胞压积的影响。而系数a1、b1、a′、b′相比较差异十分显著(P均<0.01)。
3 讨论
血液是一种非牛顿流体，其表观粘度ηa是一随切变率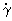
而变化的曲线[1]：
ηa=f()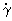
, http://www.100md.com
(7)
使用粘度计检测血标本得到的是一组在不同切变率下的表观粘度值，由于数据量过大在临床上使用时无法对所有点进行比较，一般采用三点法进行分析，这样处理存在的问题是：
(1)经过三点可以作无穷多条曲线，用三点数据无法还原出表观粘度曲线，三点法丢失的信息过多。
(2)在表观粘度的测试过程中，由于主观和客观方面的原因必然导致一定的随机误差，采用三点法表征表观粘度曲线不可能消除或降低随机误差的影响。
采用乘幂函数法表示血液表观粘度为何能降低测试过程中的随机误差呢?从信号处理的角度认为可能是由于表观粘度数据为一相关信号和而随机误差是一种非相关的信号，在数据处理过程中由于存在迭加效应从而使相关信号得到加强而无关信号被减弱所致。采用迭加平均法提高信噪比的程度与平均点数有关，为N倍。可以推论，在采用乘幂函数表示血液表观粘度时可降低测试过程中的随机误差，其减小随机误差的程度与表观粘度测试过程中的测试点数有关，点数越多对降低随机误差的效果越好，其定量分析还有待于今后大量的实验。采用乘幂函数法表示血液表观粘度有以下优点：①可降低测试过程中引入的随机误差。②表达式简洁直观，根据系数可以非常方便地得到表观粘度曲线。③系数的求取不受测试点的限制，只要测试点数多于两点即可；测试点越多随机误差的影响越小。④红细胞压积与乘幂函系数之间是一线性关系，采用一简单算法即可消除红细胞压积的影响。
, 百拇医药
在临床应用和实验研究中比较血液的表观粘度需要消除红细胞压积的影响，经典的方法是计算还原粘度[1]：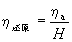
(8)
从前面的结果可知，红细胞压积对乘幂函数的系数a和b均有影响，因此红细胞压积与表观粘度之间的关系不是简单的线性关系，采用式(8)要消除红细胞压积的影响是不可能的。必须引入更为合理的算法。正常组和肺癌患者组的血液粘度比较，差异不显著；而红细胞压积比较，差异非常显著。很可能是由于红细胞压积的影响而导致两组表观粘度之间的差异不显著，有必要在消除红细胞压积的影响后再作比较。采用消除红细胞压积影响的算法后再比较，两组差异非常显著，肺癌组的血液粘度大于正常人组，这与临床观察到的现象相符[3]，不考虑红细胞压积的影响很可能作出相反的结论。由于红细胞压积与血液表观粘度之间是一非线性关系，采用简单的还原粘度算法无法消除红细胞压积的影响；而红细胞压积与乘幂系数是线性关系，采用本研究提出的消除红细胞压积的方法能较好地解决这一难题。
, 百拇医药
总之，用乘幂函数表示法比用传统的三点表示法至少将测试过程中的随机误差降低了一个数量级。红细胞压积与乘幂系数之间的关系是一线性关系，因此采用简单的数学处理方法即可消除红细胞压积的影响，但对于乘幂函数中系数a和b的生理意义，目前还无法给出确切的定义，有待进一步的实验研究和临床验证。
作者简介：尹志勇，男，35岁，副研究员，博士
参考文献
1 吴云鹏，梁子钧.生物流变学.北京：高等教育出版社，1988.1～26
2 廖福龙.临床血液生物流变学.天津：天津科学翻译出版社，1987.1～13
3 王怡，王仰宗.实用临床血液流变学.北京：学苑出版社，1994.431～436
4 Thurston G B. Effects of hematocrit on blood viscoelasticity and in establishing normal values. Biorheology,1978,15(2):239
, 百拇医药
5 Fedde M R, Wideman R F Jr. Blood viscosity in broilers:influence on pulmonary hypertension syndrome. Poult Sci,1996,75(10):1261
6 Baskurt O K, Meiselman H J. Cellular determinants of low-shear blood viscosity. Biorheology,1997,34(3):235
7 Secomb T W, Hsu R, Pries A R. A model for red blood cell motion in glycocalyx-lined capillaries. Am J Physiol,1988,274(3 Pt2):H1016
(收稿：1998-06-03；修回：1998-10-16), http://www.100md.com
单位：尹志勇 王正国 第三军医大学附属大坪医院野战外科研究所第四研究室 重庆，400042；蔡绍皙 重庆大学生物工程研究院 重庆，400044
关键词：表观粘度；乘幂函数；红细胞压积
提要 目的
提要 目的：寻找一种更为简洁有效的描述血液表观粘度的方法。方法：8例正常人和26例肺癌患者及4组用正常人自体血浆配制的不同压积血标本，首先测其表观粘度，然后用曲线拟合的方法筛选拟合方式，并对筛选出的乘幂法进行验证。结果：乘幂函数表示有利于消除血液粘度测量过程中的随机误差，红细胞压积与乘幂系数之间是一线性关系，提出了一种新的、更有效的消除红细胞压积影响的方法。结论：采用乘幂函数描述血液表观粘度是可行有效的方法。
中图法分类号 R331.1
, 百拇医药
Description of blood apparent viscosity with power function and a new method of eliminating hematocrit's interference
Yin Zhiyong, Cai Shaoxi, Wang Zhengguo
(Research Institute of Field Surgery, Daping Hospital, Third Military Medical University, Chongqing, 400042)
Abstract Objective: To seek a more laconic and effective method to describe the blood apparent viscosity. Methods: The blood samples from 8 healthy adults and 26 patients with lung cancer and 4 groups of blood samples with different hematocrits were used to obtain the apparent viscosity data. A power function was selected by curve coincidencing and validated by the apparent viscosity data. Results: The power function method was in favor of eliminating random errors in the process of measurement. The relationship between hematocrit and the coefficients of the power function was linear. Conclusion: The power function is a feasible and effective method to describe the blood apparent viscosity.
, 百拇医药
Key words apparent viscosity; power function; hematocrit
血液表观粘度是临床上常用的流变学指标，应用日益广泛[1，2]，但存在两个主要问题：一是表达形式不够理想，其次是采用还原粘度法比较不同红细胞压积下血液的流变特性时，误差较大。能否用更为简单、精确的方式表达血液表观粘度，并引入一种比还原粘度法更为有效地消除红细胞压积影响的新方法。
1 材料与方法
采取8例正常人、26例肺癌患者肝素抗凝的新鲜静脉血，并将部分取自正常献血者的红细胞分离后，用自身血浆配制成4组红细胞压积(Ht)分别为26.7%，36.0%,50.0%,66.7%的样本(每组8个样本)，分别按下法测定各样本的表观粘度。将约0.8 ml血标本注入Low Shear 30流变测定仪的Coutte氏小室中，小室内温度保持在37.0℃±0.1℃，分别在0.138, 0.187, 0.255, 0.346, 0.471, 0.639, 0.87, 1.182, 1.607, 2.19, 2.97, 4.04, 5.49, 7.46, 10.16, 13.79, 18.74, 25.5切变率处测试其表观粘度。对测得的表观粘度数据采用直线、对数、多项式、乘幂、指数、移动平均等方式进行拟合，筛选最佳拟合方式。
, http://www.100md.com
在血液表观粘度的测试过程中由于主观和客观原因会导致一些随机误差，我们在偶然的情况下观察到乘幂表示法对减少随机误差有效。为说明这一现象，采用以下方法进行分析。
随机抽取一正常人全血表观粘度数据，在其测试结果中人为加入最大值为±10%的随机误差，其计算公式为：
ηa′=ηa+(RAND()-0.5)×ηa÷5
(1)
式中ηa′为加入随机误差后的表观粘度值，ηa为原测试值，RAND()为大于等于0而又小于1的随机数。采用(1)式分别计算不同切变率处的表观粘度值并重复20次，记录每次实验数据，进行回归分析，求出系数a、b和R2，并分别计算各自的均值、标准差和标准差与均值之比。
, 百拇医药
为消除红细胞压积的影响，根据红细胞压积与乘幂系数的线性关系提出了一种新的消除红细胞压积的方法，步骤如下：
①根据测得的表观粘度数据采用回归分析计算出乘幂系数a,b。
②按下式计算a1和b1：
b1=b/Ht
(2)
③计算压积为45%处的乘幂系数a′和b′：
a′=a1×0.45-15.356
, http://www.100md.com
b′=b1×0.45
(3)
④同时也可计算压积为45%时各种切变率下的表观粘度值：
ηb′=a′
(4)
2 结果
在上述多种曲线拟合方式中，乘幂函数与血液表观粘度数据吻合得最好，即表观粘度可以用乘幂函数表示：
ηa=a
, http://www.100md.com
(5)
根据测得的表观粘度数据用回归分析可计算出每一例全血标本的表观粘度所对应的乘幂系数a、b和表征拟合程度的R2，其结果见表1。所有拟合曲线的R2都非常接近于1，因此，无论是正常人、肺癌患者，还是不同压积的血标本采用乘幂函数描述其粘度数据都是非常合适的。
表1 血液表观粘度乘幂函数系数
Tab 1 The coefficients of the power function of the blood apparent viscosity
Group
n
a
b
, 百拇医药
R2
Healthy adults
8
20.78±3.82
0.37±0.04
0.99±0.01
Lung cancer
26
20.25±7.04
0.38±0.06
0.99±0.01
Different Ht
, 百拇医药
26.7%
8
6.97±1.70
0.24±0.02
0.97±0.02
36.0%
8
10.2±2.12
0.31±0.03
0.97±0.02
50.0%
8
, http://www.100md.com 20.9±2.39
0.43±0.03
0.99±0.01
66.7%
8
34.7±3.07
0.53±0.02
0.99±0.01
在一正常人血表观粘度的测试结果中加入最大值为±10%的随机误差后，采用传统的高中低三点表示法和乘幂数表示法所得数据的统计结果见表2。
表2 加入随机误差后的表观粘度及对应的乘幂函数系数
, 百拇医药
Tab 2 The apparent viscosity and the coefficients of the power function after adding random error
Three points method
Coefficients of the power funtion
0.138(Low)
2.19(Medium)
25.5(High)
a
b
R2
, http://www.100md.com
Average(x)
62.052
21.027
8.378
29.512
0.420
0.989
Standard deviation(s)
14.147
4.362
3.853
0.390
, 百拇医药
0.007
0.003
CV(s/x)
0.228
0.207
0.460
0.013
0.016
0.003
可见采用三点法受随机误差的影响较大，其标准差与均值之比均大于20%。采用乘幂函数表示后，其比值小于2%，因此采用乘幂函数表示有利于降低随机误差的影响。
将表1中不同压积血标本的乘幂函数系数以散点图的形式表示在图1中，可见其散点图基本上分布在一条直线上，经回归分析可得乘幂函数系数与红细胞压积的回归方程：
, http://www.100md.com
a=a1H-a0=73.991H-15.356
b=b1H=0.8442H
(6)
图1 正常人红细胞压积与表观粘度乘幂函数系数的关系
Fig 1 The relationship between hematocrit of healthy adults and the coefficients of the power function
可见红细胞压积与乘幂系数之间的关系均为线性关系。
, 百拇医药
计算正常组和肺癌组在各切变率处表观粘度的均值和标准差，两组血液表观粘度比较除在切变率为25.5处P<0.05外，其余各点的差异不显著(P均>0.05)，而两组红细胞压积比较差异十分显著。根据实验数据分别计算出正常组和肺癌组乘幂系数a和b，然后按式(2)计算与红细胞压积无关的系数a1和b1，再按式(3)计算红细胞压积为45%时的乘幂系数a′和b′，其结果见表3。
表3 正常组和肺癌组乘幂系数及消除红细胞压积后的系数比较
Tab 3 The comparison of the coefficients of the power function
a
b
a1
, http://www.100md.com
b1
a′(45%)
b′(45%)
Healthy adults
20.779±3.820
0.368±0.040
80.354±5.793
0.819±0.077
30.803±2.607
0.369±0.034
Lung cancer
, http://www.100md.com
20.249±7.037
0.379±0.060
93.461±20.77
0.997±0.199
26.701±9.348
0.449±0.090
T test
0.430469
0.211893
0.00388
0.000435
, http://www.100md.com 0.00388
0.000435
正常组和肺癌组的系数a和b的差异不显著(P<0.05)，这与直接采用表观粘度值分析得出的结论一致，二者都没有消除红细胞压积的影响。而系数a1、b1、a′、b′相比较差异十分显著(P均<0.01)。
3 讨论
血液是一种非牛顿流体，其表观粘度ηa是一随切变率
而变化的曲线[1]：ηa=f(
), http://www.100md.com
(7)
使用粘度计检测血标本得到的是一组在不同切变率下的表观粘度值，由于数据量过大在临床上使用时无法对所有点进行比较，一般采用三点法进行分析，这样处理存在的问题是：
(1)经过三点可以作无穷多条曲线，用三点数据无法还原出表观粘度曲线，三点法丢失的信息过多。
(2)在表观粘度的测试过程中，由于主观和客观方面的原因必然导致一定的随机误差，采用三点法表征表观粘度曲线不可能消除或降低随机误差的影响。
采用乘幂函数法表示血液表观粘度为何能降低测试过程中的随机误差呢?从信号处理的角度认为可能是由于表观粘度数据为一相关信号和而随机误差是一种非相关的信号，在数据处理过程中由于存在迭加效应从而使相关信号得到加强而无关信号被减弱所致。采用迭加平均法提高信噪比的程度与平均点数有关，为N倍。可以推论，在采用乘幂函数表示血液表观粘度时可降低测试过程中的随机误差，其减小随机误差的程度与表观粘度测试过程中的测试点数有关，点数越多对降低随机误差的效果越好，其定量分析还有待于今后大量的实验。采用乘幂函数法表示血液表观粘度有以下优点：①可降低测试过程中引入的随机误差。②表达式简洁直观，根据系数可以非常方便地得到表观粘度曲线。③系数的求取不受测试点的限制，只要测试点数多于两点即可；测试点越多随机误差的影响越小。④红细胞压积与乘幂函系数之间是一线性关系，采用一简单算法即可消除红细胞压积的影响。
, 百拇医药
在临床应用和实验研究中比较血液的表观粘度需要消除红细胞压积的影响，经典的方法是计算还原粘度[1]：
(8)
从前面的结果可知，红细胞压积对乘幂函数的系数a和b均有影响，因此红细胞压积与表观粘度之间的关系不是简单的线性关系，采用式(8)要消除红细胞压积的影响是不可能的。必须引入更为合理的算法。正常组和肺癌患者组的血液粘度比较，差异不显著；而红细胞压积比较，差异非常显著。很可能是由于红细胞压积的影响而导致两组表观粘度之间的差异不显著，有必要在消除红细胞压积的影响后再作比较。采用消除红细胞压积影响的算法后再比较，两组差异非常显著，肺癌组的血液粘度大于正常人组，这与临床观察到的现象相符[3]，不考虑红细胞压积的影响很可能作出相反的结论。由于红细胞压积与血液表观粘度之间是一非线性关系，采用简单的还原粘度算法无法消除红细胞压积的影响；而红细胞压积与乘幂系数是线性关系，采用本研究提出的消除红细胞压积的方法能较好地解决这一难题。
, 百拇医药
总之，用乘幂函数表示法比用传统的三点表示法至少将测试过程中的随机误差降低了一个数量级。红细胞压积与乘幂系数之间的关系是一线性关系，因此采用简单的数学处理方法即可消除红细胞压积的影响，但对于乘幂函数中系数a和b的生理意义，目前还无法给出确切的定义，有待进一步的实验研究和临床验证。
作者简介：尹志勇，男，35岁，副研究员，博士
参考文献
1 吴云鹏，梁子钧.生物流变学.北京：高等教育出版社，1988.1～26
2 廖福龙.临床血液生物流变学.天津：天津科学翻译出版社，1987.1～13
3 王怡，王仰宗.实用临床血液流变学.北京：学苑出版社，1994.431～436
4 Thurston G B. Effects of hematocrit on blood viscoelasticity and in establishing normal values. Biorheology,1978,15(2):239
, 百拇医药
5 Fedde M R, Wideman R F Jr. Blood viscosity in broilers:influence on pulmonary hypertension syndrome. Poult Sci,1996,75(10):1261
6 Baskurt O K, Meiselman H J. Cellular determinants of low-shear blood viscosity. Biorheology,1997,34(3):235
7 Secomb T W, Hsu R, Pries A R. A model for red blood cell motion in glycocalyx-lined capillaries. Am J Physiol,1988,274(3 Pt2):H1016
(收稿：1998-06-03；修回：1998-10-16), http://www.100md.com