肌红蛋白和血红蛋白氧饱和度的热力学分析
作者：吴清才 王宪民
单位：航天医学工程研究所，北京 100094
关键词：肌红蛋白；血红蛋白；血氧饱和度；热力学
航天医学与医学工程990416摘要：目的 用热力学分析方法对肌红蛋白和血红蛋白氧饱和度进行分析。方法 从热力学角度，利用Gibbs自由能、熵、内能等概念进行分析。结果 得出了与试验结果及前人分析相符合的结果。结论 利用热力学方法对肌红蛋白和血红蛋白氧饱和度进行分析是可行的。
中图分类号：R319 文献标识码：A 文章编号：1002-0837(1999)04-0298-05
Thermodynamic Analysis of Saturation Degree of O2 in Myoglobin and Hemoglobin
, 百拇医药
WU Qing-cai,WANG Xian-min
Abstract: Objective To analyze the saturation degree of O2 in myoglobin and hemoglobin. Method Analysis is based on thermodynamic concepts such as Gibbs free energy, entropy,internal energy and so on. Result The analytical result were consistent with the results of experiments and analysis made by other authors.Conclusion The thermodynamic method is feasible in analysing O2 saturation degree in myoglobin and hemoglobin.
, 百拇医药
Key words：myoglobin;hemoglobin;oxygen saturation rate;thermodynamics
Address reprint requests to:WU Qing-cai.Institute of Space Medico-Engineering,Beijing 100094,China
在脊椎动物中氧载体的蛋白质为血红蛋白和肌红蛋白。血红蛋白包含在血红细胞中，在血液中起着氧载体的作用，血红蛋白承担了把98%的氧运输到肌体组织的工作。肌红蛋白位于肌肉组织液中，起着储存氧的作用，并便于氧在肌肉中的转移，作为血红蛋白氧的应急供应[1]。因此二者的氧饱和度直接关系到肌体的生命活动。
航天领域中压力应急时，大气PO2下降导致肺泡内的PO2降低，亦即氧饱和度降低，从而引起缺氧症状，包括：呼吸节律异常、循环代偿障碍亦即脑功能的改变等。因此，对肌红蛋白和血红蛋白的氧饱和度进行分析是非常有意义的。
, http://www.100md.com
Lubert Stryer[1]从化学平衡的角度对肌红蛋白氧饱和度进行了分析， Hill引入了协作性的概念，也是从化学平衡的角度对血红蛋白氧饱和度进行了分析，都得出了基本上与试验结果相符合的结果。由于血液和组织液中的变化过程是等温等压过程，本文将从热力学角度建立热力学分析模型，利用Gibbs自由能、熵、内能等概念对肌红蛋白和血红蛋白氧饱和度进行分析，以助于研究肌体的生理状态。
热力学分析模型—稀溶液模型
肌红蛋白是肌肉组织中由单个折叠链构成的蛋白质，可以结合一个氧分子，因此肌红蛋白的氧饱和度可以表示为：
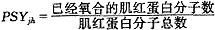(1)
由于O2、肌红蛋白与组织液相比，所占比例很小，我们可以把O2、肌红蛋白为溶质、组织液为溶剂的溶液看作是稀溶液，O2、肌红蛋白作为自由分子存在于组织液中。
, 百拇医药
血红蛋白是一种比肌红蛋白复杂得多的蛋白质，是由4条链构成的一种变构蛋白质，可以结合1、2、3或4个氧分子。因此血红蛋白的氧饱和度可以表示为：
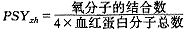(2)
同样，由于O2、血红蛋白与血浆相比，所占比例很小，我们可以把O2、血红蛋白为溶质、血浆为溶剂的溶液看作是稀溶液，O2、血红蛋白作为自由分子存在于血浆中。
溶液是个复合系统，可以用于研究很多重要而有意义的平衡问题。在生理学上一个重要的问题就是气体在液体中的溶解度，此时的平衡发生在气相的纯气体和溶解在溶液中的气体之间，气体的饱和浓度取决于温度和压力。这些平衡问题可以用Gibbs自由能原理来研究，为此要找出一个用压力、温度、溶液各成分的摩尔数表示的Gibbs自由能表达式。
, 百拇医药
为了描述溶液，对占有体积V的系统中，各部分处于等温T、等压P时，各成分的摩尔数为：n1、n2、n3、……，其中n1总是表示溶剂的摩尔数，n2、n3、……为各溶质的摩尔数。则Gibbs自由能可表示为[2，3]：
G(T,P,n1,n2,n3,…)=E+PV-TS(3)
应指出，V并不恰好是同一压力和同一温度下各溶液组分的体积之和，根据体积的广延性质可求出体积和摩尔数之间的关系[3～5],对于只有一种溶质的二元溶液有：
V(T,P,n1,n2)=n1υ(T,P,x)(4)
, http://www.100md.com
其中x＝n2/n1，对于稀溶液，x<<1有：
υ(T,P,x)＝υ1(T,P)+x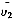
(T,P)+O(x2)≈υ1(T,P)+x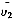(T,P)(5)
其中υ1(T,P)表示纯溶剂的摩尔体积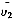，(T,P)(T,P,x)=
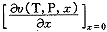表示浓度为0时溶质的分摩尔体积。将式(5)代入式(4)得：
, 百拇医药
V(T,P,n1,n2)≈n1υ1(T,P)+n2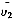(T,P)(6)
同样根据能量的广延性有：
0E(T,P,n1,n2)≈n1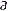
1(T,P)+n2
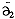(T,P)(7)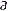1(T,P)为纯溶剂的摩尔能量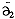，(T,P)为溶质的分摩尔能量。对于熵S，还要考虑溶剂和溶质的混合熵△Sh:
, 百拇医药
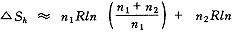
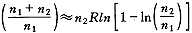(n1>>n2)(8)
则S(T,P,n1,n2)≈n1S1(T,P)+n2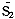
(T,P)+△Sh≈n1S1(T,P)+n2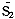(T,P)+n2R
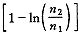(9)
, http://www.100md.com
将式(6)(7)(9)代入式(3)得稀溶液的Gibbs自由能：
G(T,P,n1,n2)≈n1g1(T,P)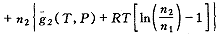
(10)
g1(T,P)为纯溶剂的摩尔自由能，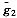
(T,P)为溶质的分摩尔自由能。
肌红蛋白的氧饱和度分析
肌红蛋白氧饱和度是组织液中溶解的O2与肌红蛋白结合O2之间达到热力学平衡的结果。而组织液中溶解的O2与氧分压PO2有直接关系。我们的目的就是要找出肌红蛋白氧饱和度与氧分压PO2的关系。图1是肌红蛋白氧饱和度的试验曲线[1]。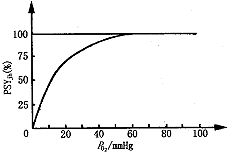
, 百拇医药
图1 肌红蛋白的氧饱和度试验曲线
Fig.1 Experimental curve of the saturation degree of O2 in myoglobin
令n1、no、njh分别代表组织液、被溶解的氧和被溶解的肌红蛋白的摩尔数。肌红蛋白有氧合的和非氧合的，首先作为单质考虑，由式(10)加以推广写出Gibbs自由能G0，而后加上修正项△G。
G0＝n1g1(T,P)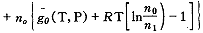
(11)
肌红蛋白有氧合的和非氧合的两部分：
, http://www.100md.com
njh＝n0jh+n1jh(12)
n0jh 、n1jh分别表示非氧合和氧合肌红蛋白的摩尔数。非氧合和氧合肌红蛋白混合熵增量为：
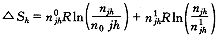(13)
两种不同形态的肌红蛋白具有不同能量而引起的能量差为：
△E=n1jh△E10(14)
其中△E10表示氧合与非氧合分子之间的摩尔能量差。因此式(11)的修正项为：
, 百拇医药
△G=△E-T△S (△V=0)(15)
将式(15)加到式(11)上得：
G＝n1g1(T,P)+no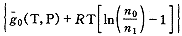
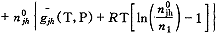
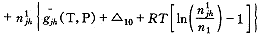(16)
当平衡时，氧分子的增加量δn即为氧合肌红蛋白的减少量。此时Gibbs自由能保持不变，即：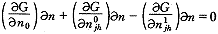
(17)
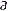其中G/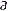ni为各组分的化学势,即
, 百拇医药
μ0=μ1jh(18)
其物理意义是：平衡时已溶氧分子的化学势必须等于氧合和脱氧合肌红蛋白化学势μ0之差。
由式(16)可得：
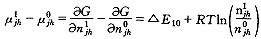(19)
以上讨论分析了已溶氧分子与肌红蛋白氧合程度间的平衡，得出重要结论(18)式。下面讨论气相氧与已溶于组织液中的液相氧间的平衡。气相和液相氧之间的平衡要求应μ0等于气相氧的化学势μg,而
(20)
, 百拇医药
其中k为玻尔兹曼常数，可见对于等温过程，μ0仅取决于氧分压μO2。
由式(1)的氧饱和度为：
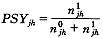(21)
将式(18)(19)(20)(21)联立得：
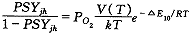(22)
令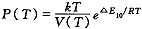
表示依赖于温度的基准压力，则
, 百拇医药
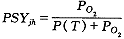(23)
血红蛋白的氧饱和度分析
血红蛋白与肌红蛋白的主要差别在于，血红蛋白有4个位置可供氧分子附着，而肌红蛋白只有一个位置。因此血红蛋白有结合0、1、2、3或4个氧分子的5种可能。血红蛋白氧饱和度是血浆中溶解的O2与外界氧气压强以及血红蛋白结合O2之间达到热力学复合平衡的结果。如图2曲线a是体温37℃和血浆离子浓度为正常值时的血红蛋白氧饱和度试验曲线[1，3]。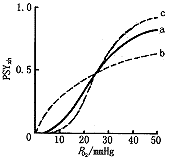
图2 血红蛋白的氧饱和度曲线介于非协作结合b和完全协作结合a的曲线之间
, 百拇医药 Fig.2 The saturation degree of O2 curve in hemoglobin
如果按照上面讨论肌红蛋白的思路和方法，再结合氧合血红蛋白可能呈现的5种状态，计算Gibbs自由能的附加项，计算过程将非常复杂。但仍得到和 (23)式一样的结论，这与图2的S形试验曲线完全不同。其原因为：在分子方面，血红蛋白的氧的结合之间具有“协作性”。“协作性”是指，血红蛋白加上一个O2所引起的能量变化与以往结合的氧分子数有关，而不是每加一个O2的能量变化都是一样的。
我们可以考虑一种极端情况，即只考虑脱氧合血红蛋白和结合4个氧分子的血红蛋白。令nxj、no、n0xh 、n4xh分别代表血浆、被溶解的氧、被溶解的脱氧合血红蛋白和结合4个氧分子的血红蛋白的摩尔数，△E40代表结合4个氧分子的能量变化。则(16)式变为：
, http://www.100md.com
G＝nxjgxj(T,P)+no
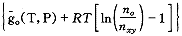
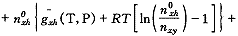
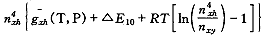(24)
当处于平衡时，血浆中氧分子的增加量δn即为氧合肌红蛋白的减少量的4倍。此时的Gibbs自由能函数保持不变，(18)式变为：
4μo=μ4xh-μ0xh(25)
其物理意义是：平衡时已溶氧分子的化学势μo必须等于氧合和脱氧合血红蛋白化学势之差。由(24)式得：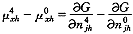
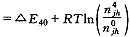(26)
, http://www.100md.com
由(2)式得血红蛋白的氧饱和度：
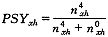(27)
将(20)(25)(26)(27)式联立得:
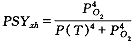(28)
其中PCT表示依赖于温度的基准压力。
用式(28)描出一个S形曲线，如图2中的c曲线所示。可见c曲线比试验曲线a 要陡，也就是说此模型过于极端了。但可以给出血红蛋白氧饱和度曲线的一个范围，介于结合一个氧分子的非协作结合和结合4个氧分子的完全协作结合之间。那么怎样才能确定一个结合过程的协作程度呢？我们引入一个协作度的概念，用n表示。(28)式可改写为：
, 百拇医药
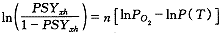(29)
可作出一条斜率为n的直线，称为Hill图，此时的n即为协作度。如图3所示。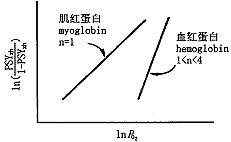
图3 肌红蛋白和血红蛋白结合氧的Hill图
Fig.3 Hill chart of hemoglobin and myoglobin on combined with O2
讨 论
由(23)式可得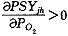
和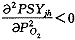
,即氧饱和度曲线为单增上凸函数，在PO2＝0时斜率最大。且当PO2>>P(T)时，PSYjh→1和试验氧饱和曲线(图1)形状一致。
, 百拇医药
由(28)式可得当PO2>>P(T)时，PSYjh→1。对(23)式求导可得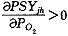,即血红蛋白的氧饱和度曲线也是单增曲线，且在PO2<0.88P(T)时，
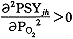，即为下凸曲线；PO2>0.88P(T)时，
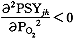,即为上凸曲线。和试验所得的S形曲线相符合(图2)。如图3，对于肌红蛋白，n=1，意味着氧分子的结合是相互独立的；相反，对于血红蛋白，1
结 论
利用热力学方法对肌红蛋白和血红蛋白氧饱和度进行分析简单、实用、机理表达清楚，得出的结果与试验结果及前人分析结果相符合。因此，利用热力学方法对肌红蛋白和血红蛋白氧饱和度进行分析是切实可行的。
参考文献
[1]Lubert Stryer.Biochemistry(second edition)[M]. W.H.Freeman and Company,1980:32～63
[2]Kenneth Wark Jr.Advanced thermodynamics for engineers[M].New York:McGraw-Hill,Inc,1995:39～79
[3]黄诒焯，郑筱祥主编.生理功能的工程分析[M].北京:高等教育出版社，1993：5～43
, http://www.100md.com
[4]Smith CJ.Problems with entropy in biology[J].Biosystems,1975，7:259～265
[5]Wisniewski S,Staniszewski B，Szymanik R.Thermodynamics of Nonequilibrium Processes[M].New York: D.Reidel Publishing Company,1976:55～200
[6]Morowitz HJ.Entropy for Biologists. An introduction to Thermodynamics [M]. New York: Academic Press, 1970:70～123
收稿日期：1998-11-16, 百拇医药
单位：航天医学工程研究所，北京 100094
关键词：肌红蛋白；血红蛋白；血氧饱和度；热力学
航天医学与医学工程990416摘要：目的 用热力学分析方法对肌红蛋白和血红蛋白氧饱和度进行分析。方法 从热力学角度，利用Gibbs自由能、熵、内能等概念进行分析。结果 得出了与试验结果及前人分析相符合的结果。结论 利用热力学方法对肌红蛋白和血红蛋白氧饱和度进行分析是可行的。
中图分类号：R319 文献标识码：A 文章编号：1002-0837(1999)04-0298-05
Thermodynamic Analysis of Saturation Degree of O2 in Myoglobin and Hemoglobin
, 百拇医药
WU Qing-cai,WANG Xian-min
Abstract: Objective To analyze the saturation degree of O2 in myoglobin and hemoglobin. Method Analysis is based on thermodynamic concepts such as Gibbs free energy, entropy,internal energy and so on. Result The analytical result were consistent with the results of experiments and analysis made by other authors.Conclusion The thermodynamic method is feasible in analysing O2 saturation degree in myoglobin and hemoglobin.
, 百拇医药
Key words：myoglobin;hemoglobin;oxygen saturation rate;thermodynamics
Address reprint requests to:WU Qing-cai.Institute of Space Medico-Engineering,Beijing 100094,China
在脊椎动物中氧载体的蛋白质为血红蛋白和肌红蛋白。血红蛋白包含在血红细胞中，在血液中起着氧载体的作用，血红蛋白承担了把98%的氧运输到肌体组织的工作。肌红蛋白位于肌肉组织液中，起着储存氧的作用，并便于氧在肌肉中的转移，作为血红蛋白氧的应急供应[1]。因此二者的氧饱和度直接关系到肌体的生命活动。
航天领域中压力应急时，大气PO2下降导致肺泡内的PO2降低，亦即氧饱和度降低，从而引起缺氧症状，包括：呼吸节律异常、循环代偿障碍亦即脑功能的改变等。因此，对肌红蛋白和血红蛋白的氧饱和度进行分析是非常有意义的。
, http://www.100md.com
Lubert Stryer[1]从化学平衡的角度对肌红蛋白氧饱和度进行了分析， Hill引入了协作性的概念，也是从化学平衡的角度对血红蛋白氧饱和度进行了分析，都得出了基本上与试验结果相符合的结果。由于血液和组织液中的变化过程是等温等压过程，本文将从热力学角度建立热力学分析模型，利用Gibbs自由能、熵、内能等概念对肌红蛋白和血红蛋白氧饱和度进行分析，以助于研究肌体的生理状态。
热力学分析模型—稀溶液模型
肌红蛋白是肌肉组织中由单个折叠链构成的蛋白质，可以结合一个氧分子，因此肌红蛋白的氧饱和度可以表示为：
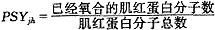(1)由于O2、肌红蛋白与组织液相比，所占比例很小，我们可以把O2、肌红蛋白为溶质、组织液为溶剂的溶液看作是稀溶液，O2、肌红蛋白作为自由分子存在于组织液中。
, 百拇医药
血红蛋白是一种比肌红蛋白复杂得多的蛋白质，是由4条链构成的一种变构蛋白质，可以结合1、2、3或4个氧分子。因此血红蛋白的氧饱和度可以表示为：
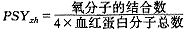(2)同样，由于O2、血红蛋白与血浆相比，所占比例很小，我们可以把O2、血红蛋白为溶质、血浆为溶剂的溶液看作是稀溶液，O2、血红蛋白作为自由分子存在于血浆中。
溶液是个复合系统，可以用于研究很多重要而有意义的平衡问题。在生理学上一个重要的问题就是气体在液体中的溶解度，此时的平衡发生在气相的纯气体和溶解在溶液中的气体之间，气体的饱和浓度取决于温度和压力。这些平衡问题可以用Gibbs自由能原理来研究，为此要找出一个用压力、温度、溶液各成分的摩尔数表示的Gibbs自由能表达式。
, 百拇医药
为了描述溶液，对占有体积V的系统中，各部分处于等温T、等压P时，各成分的摩尔数为：n1、n2、n3、……，其中n1总是表示溶剂的摩尔数，n2、n3、……为各溶质的摩尔数。则Gibbs自由能可表示为[2，3]：
G(T,P,n1,n2,n3,…)=E+PV-TS(3)
应指出，V并不恰好是同一压力和同一温度下各溶液组分的体积之和，根据体积的广延性质可求出体积和摩尔数之间的关系[3～5],对于只有一种溶质的二元溶液有：
V(T,P,n1,n2)=n1υ(T,P,x)(4)
, http://www.100md.com
其中x＝n2/n1，对于稀溶液，x<<1有：
υ(T,P,x)＝υ1(T,P)+x
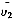(T,P)+O(x2)≈υ1(T,P)+x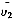(T,P)(5)其中υ1(T,P)表示纯溶剂的摩尔体积，
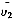(T,P)(T,P,x)=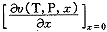表示浓度为0时溶质的分摩尔体积。将式(5)代入式(4)得：, 百拇医药
V(T,P,n1,n2)≈n1υ1(T,P)+n2
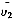(T,P)(6)同样根据能量的广延性有：
0E(T,P,n1,n2)≈n1
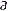1(T,P)+n2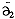(T,P)(7)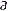1(T,P)为纯溶剂的摩尔能量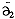，(T,P)为溶质的分摩尔能量。对于熵S，还要考虑溶剂和溶质的混合熵△Sh:, 百拇医药
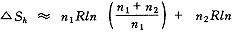
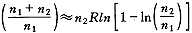(n1>>n2)(8)则S(T,P,n1,n2)≈n1S1(T,P)+n2
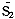(T,P)+△Sh≈n1S1(T,P)+n2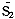(T,P)+n2R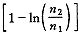(9), http://www.100md.com
将式(6)(7)(9)代入式(3)得稀溶液的Gibbs自由能：
G(T,P,n1,n2)≈n1g1(T,P)
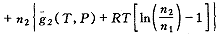(10)g1(T,P)为纯溶剂的摩尔自由能，
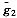(T,P)为溶质的分摩尔自由能。肌红蛋白的氧饱和度分析
肌红蛋白氧饱和度是组织液中溶解的O2与肌红蛋白结合O2之间达到热力学平衡的结果。而组织液中溶解的O2与氧分压PO2有直接关系。我们的目的就是要找出肌红蛋白氧饱和度与氧分压PO2的关系。图1是肌红蛋白氧饱和度的试验曲线[1]。
, 百拇医药
图1 肌红蛋白的氧饱和度试验曲线
Fig.1 Experimental curve of the saturation degree of O2 in myoglobin
令n1、no、njh分别代表组织液、被溶解的氧和被溶解的肌红蛋白的摩尔数。肌红蛋白有氧合的和非氧合的，首先作为单质考虑，由式(10)加以推广写出Gibbs自由能G0，而后加上修正项△G。
G0＝n1g1(T,P)
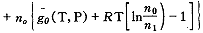(11)肌红蛋白有氧合的和非氧合的两部分：
, http://www.100md.com
njh＝n0jh+n1jh(12)
n0jh 、n1jh分别表示非氧合和氧合肌红蛋白的摩尔数。非氧合和氧合肌红蛋白混合熵增量为：
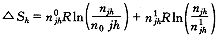(13)两种不同形态的肌红蛋白具有不同能量而引起的能量差为：
△E=n1jh△E10(14)
其中△E10表示氧合与非氧合分子之间的摩尔能量差。因此式(11)的修正项为：
, 百拇医药
△G=△E-T△S (△V=0)(15)
将式(15)加到式(11)上得：
G＝n1g1(T,P)+no
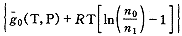
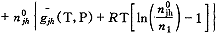
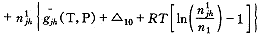(16)当平衡时，氧分子的增加量δn即为氧合肌红蛋白的减少量。此时Gibbs自由能保持不变，即：
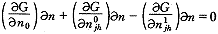(17)其中
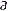G/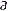ni为各组分的化学势,即, 百拇医药
μ0=μ1jh(18)
其物理意义是：平衡时已溶氧分子的化学势必须等于氧合和脱氧合肌红蛋白化学势μ0之差。
由式(16)可得：
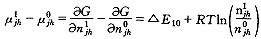(19)以上讨论分析了已溶氧分子与肌红蛋白氧合程度间的平衡，得出重要结论(18)式。下面讨论气相氧与已溶于组织液中的液相氧间的平衡。气相和液相氧之间的平衡要求应μ0等于气相氧的化学势μg,而
(20), 百拇医药
其中k为玻尔兹曼常数，可见对于等温过程，μ0仅取决于氧分压μO2。
由式(1)的氧饱和度为：
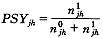(21)将式(18)(19)(20)(21)联立得：
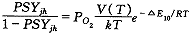(22)令
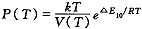表示依赖于温度的基准压力，则, 百拇医药
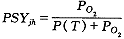(23)血红蛋白的氧饱和度分析
血红蛋白与肌红蛋白的主要差别在于，血红蛋白有4个位置可供氧分子附着，而肌红蛋白只有一个位置。因此血红蛋白有结合0、1、2、3或4个氧分子的5种可能。血红蛋白氧饱和度是血浆中溶解的O2与外界氧气压强以及血红蛋白结合O2之间达到热力学复合平衡的结果。如图2曲线a是体温37℃和血浆离子浓度为正常值时的血红蛋白氧饱和度试验曲线[1，3]。
图2 血红蛋白的氧饱和度曲线介于非协作结合b和完全协作结合a的曲线之间
, 百拇医药 Fig.2 The saturation degree of O2 curve in hemoglobin
如果按照上面讨论肌红蛋白的思路和方法，再结合氧合血红蛋白可能呈现的5种状态，计算Gibbs自由能的附加项，计算过程将非常复杂。但仍得到和 (23)式一样的结论，这与图2的S形试验曲线完全不同。其原因为：在分子方面，血红蛋白的氧的结合之间具有“协作性”。“协作性”是指，血红蛋白加上一个O2所引起的能量变化与以往结合的氧分子数有关，而不是每加一个O2的能量变化都是一样的。
我们可以考虑一种极端情况，即只考虑脱氧合血红蛋白和结合4个氧分子的血红蛋白。令nxj、no、n0xh 、n4xh分别代表血浆、被溶解的氧、被溶解的脱氧合血红蛋白和结合4个氧分子的血红蛋白的摩尔数，△E40代表结合4个氧分子的能量变化。则(16)式变为：
, http://www.100md.com
G＝nxjgxj(T,P)+no
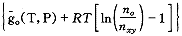
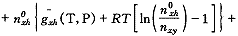
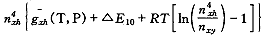(24)当处于平衡时，血浆中氧分子的增加量δn即为氧合肌红蛋白的减少量的4倍。此时的Gibbs自由能函数保持不变，(18)式变为：
4μo=μ4xh-μ0xh(25)
其物理意义是：平衡时已溶氧分子的化学势μo必须等于氧合和脱氧合血红蛋白化学势之差。由(24)式得：
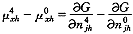
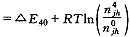(26), http://www.100md.com
由(2)式得血红蛋白的氧饱和度：
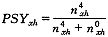(27)将(20)(25)(26)(27)式联立得:
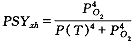(28)其中PCT表示依赖于温度的基准压力。
用式(28)描出一个S形曲线，如图2中的c曲线所示。可见c曲线比试验曲线a 要陡，也就是说此模型过于极端了。但可以给出血红蛋白氧饱和度曲线的一个范围，介于结合一个氧分子的非协作结合和结合4个氧分子的完全协作结合之间。那么怎样才能确定一个结合过程的协作程度呢？我们引入一个协作度的概念，用n表示。(28)式可改写为：
, 百拇医药
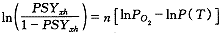(29)可作出一条斜率为n的直线，称为Hill图，此时的n即为协作度。如图3所示。
图3 肌红蛋白和血红蛋白结合氧的Hill图
Fig.3 Hill chart of hemoglobin and myoglobin on combined with O2
讨 论
由(23)式可得
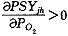和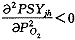,即氧饱和度曲线为单增上凸函数，在PO2＝0时斜率最大。且当PO2>>P(T)时，PSYjh→1和试验氧饱和曲线(图1)形状一致。, 百拇医药
由(28)式可得当PO2>>P(T)时，PSYjh→1。对(23)式求导可得
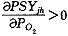,即血红蛋白的氧饱和度曲线也是单增曲线，且在PO2<0.88P(T)时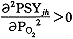，，即为下凸曲线；PO2>0.88P(T)时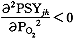，,即为上凸曲线。和试验所得的S形曲线相符合(图2)。如图3，对于肌红蛋白，n=1，意味着氧分子的结合是相互独立的；相反，对于血红蛋白，1结 论
利用热力学方法对肌红蛋白和血红蛋白氧饱和度进行分析简单、实用、机理表达清楚，得出的结果与试验结果及前人分析结果相符合。因此，利用热力学方法对肌红蛋白和血红蛋白氧饱和度进行分析是切实可行的。
参考文献
[1]Lubert Stryer.Biochemistry(second edition)[M]. W.H.Freeman and Company,1980:32～63
[2]Kenneth Wark Jr.Advanced thermodynamics for engineers[M].New York:McGraw-Hill,Inc,1995:39～79
[3]黄诒焯，郑筱祥主编.生理功能的工程分析[M].北京:高等教育出版社，1993：5～43
, http://www.100md.com
[4]Smith CJ.Problems with entropy in biology[J].Biosystems,1975，7:259～265
[5]Wisniewski S,Staniszewski B，Szymanik R.Thermodynamics of Nonequilibrium Processes[M].New York: D.Reidel Publishing Company,1976:55～200
[6]Morowitz HJ.Entropy for Biologists. An introduction to Thermodynamics [M]. New York: Academic Press, 1970:70～123
收稿日期：1998-11-16, 百拇医药