小波尺度图分析法及其在超声血流多普勒信号中的应用
作者：张平 刘颖 刘志言 沈毅 于建宏
单位：张平(中国航天科技集团公司704所，北京 100076)；刘颖(哈尔滨市第一医院内分泌科，哈尔滨 150010)；刘志言 沈毅(哈尔滨工业大学控制工程系，哈尔滨 150001)；于建宏(中国人民解放军211医院，哈尔滨 150000)
关键词：小波变换；付里叶变换；多普勒信号；血流；频谱分析
航天医学与医学工程000209摘要： 目的 将现代小波尺度图分析方法应用到人体血流多普勒信号的谱估计之中，计算血流多普勒信号的功率谱，得到小波意义上的尺度图。 方法 从时频分布的观点，小波尺度图是一种仿射平滑的Wigner-Ville分布，具有恒“Q”特性的时间频率分析窗，对于人体颈总动脉的仿真多普勒血流信号，进行了小波尺度图的研究。 结果 通过血流多普勒信号的小波尺度图研究，发现利用小波尺度图可以提高血流多普勒信号低频段的频谱分辨率。 结论 利用小波方法估计人体血流多普勒信号的频谱特性是可行的，估计结果的低频段频谱的分辨率较高，从而可以提高小血管中低速血流的估计精度。
, http://www.100md.com
中图法分类号：R319；R540.4 文献标识码：A 文章编号：1002-0837(2000)02-0119-05
Analysis of Wavelet Scalogram of Blood Flow Ultrasonic Doppler Signal.
ZHANG Ping,LIU Ying,LIU Zhi-yan，SHEN Yi,YU Jian-hong.
Abstract: Objective To study the power spectrum density of blood flow ultrasonic Doppler signal using wavelet analysis. Method Doppler signal of blood flow in human common carotid artery was studied with wavelet scalogram analysis, an affine smoothing Wigner-Ville transform with a constant “Q" character. Result Wavelet scalogram of blood flow ultrasonic signal had a higher distinguishability than STFT spectrogram in the low frequency portion, but had poorer decussation terms than spectrogram. Conclusion It is practicable to estimate the spectrum of Doppler signals of blood flow by the wavelet analysis method. And this can be used in low speed blood flow for higher resolution of spectrum in the low frequency portion.
, 百拇医药
Key words:wavelet transform;fourier transform;doppler signal;blood flow;spectrum analysis
对于平稳信号的处理工具仍然是Fourier变换，但是，在实际应用中的绝大多数信号是非平稳的，现在看来处理非平稳信号的主要工具将是小波变换，这主要是因为传统的Fourier变换分析信号时，时间和频率分辨率精度是固定不变的，而利用小波变换分析信号，在信号高频段时间分辨率精度也较高，在信号低频段频率分辨率精度较高，这很符合非平稳信号的特点。因此利用小波变换进行非平稳信号的分析可以得到较好的时间和频率估计精度[1]。超声多普勒血流信号的分析技术由于能可靠而灵敏地用于血管疾病的诊断，逐渐成为临床医学的一种重要诊断手段，尤其在心血管疾病的研究及临床诊断中有重要的意义，采用声谱图进行血流状态的分析更是受到普遍的承认，这主要是因为多普勒回波信号的动态功率谱中包含了血流的速度、方向等多方面的信息[2]。但是，采用小波尺度图来讨论分析医疗超声血流多普勒信号的谱特性还没有人研究[3，4]，本文旨在采用小波变换来进行信号的谱特性分析，同时对信号的功率谱特性进行比较，得到一些有意义的结果。
, http://www.100md.com
小波变换(WT)的恒“Q”特性时间—频率窗
古典Fourier分析是对所有时间的积分得到，只能获得整个信号的频谱，不能得到信号在某一时间段上的频率特性。从时频分布的观点来看，其频域的分辨率为最高(可以定义到某一根谱线)，但其时域分辨率为无穷小(即变换后不能提供任何时域中的信息)。鉴于以上原因，Gabor在1948年提出了加窗的短时付立叶变换思想，它在付立叶变换的基础上引入了一个时间域内局部化的“窗函数”，通过以上的方法虽然可以得到某一时间段内的频率特性，但还是存在如下的缺点：窗函数的宽度固定不变，其时域和频域的分辨率是固定不变的，不能满足一般情况下的需要，即：在信号的高频段时间窗应该短些，以利于观察信号的剧烈变化，而在低频率段时间窗要宽一些，以利于看到信号的全貌和更精细的频率信息。小波分析从根本上解决了上述缺点，使其有很大的应用灵活性和广泛性，如果定义一个函数h(t)且有：∫|th(t)|2dt<+∞,h∈L2(R)，，则称该函数为一个窗函数，且该函数的窗中心和窗半径分别由下式来确定：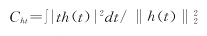
(1)
(2)
, 百拇医药
数值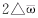
就是窗函数的宽度，同样，如果窗函数的Fourier变换也满足窗函数的条件，即：H(ω)=
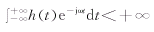一个实际信号在该窗函数作用下进行的Fourier变换就表明了信号在如下窗内的信息: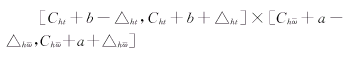
其中，a,b分别为信号在时域内和频域内的中心，而关于f∈L2(R)的连续小波变换定义为：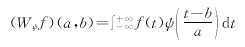
(3)
其中，ψ(t)∈L2(R),并满足容许条件，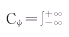
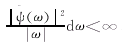,则称ψ为一个小波母函数或基小波，对于小波的一个重要性质是小波函数是一个窗函数，其时间窗和频率窗分别为: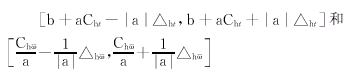
, 百拇医药
其中，a是小波变换的尺度，b是小波变换在时间轴上的时间值。从上面的式子可以看出，窗的形状随着参数a的变化而变化，b变大，时间窗增大，频率窗变小，小波对应的频率成分也变小，适合分析低频信号；反之，b变小，时间窗增小，频率窗变大，小波对应的频率成分也变高，则适合分析高频信号，这就是小波分析较短时Fourier变换优越的特点。
尺度图的时间—频率分析特性研究
随着对非平稳信号处理研究的深入，现代时间-频率分析技术得到广泛的研究和应用，谱图和尺度图是时间频率分析中二次型时频表示中的最简单的两种情况，谱图可以看成是一组带通滤波器带宽与分析频率无关的一类分析滤波器输出幅值的平方，而尺度图则是采用滤波器的带宽与分析的频率成正比的一类分析滤波器输出幅值的平方，可以看成为一类“恒Q”形式的谱图。
对于能量型的二次时频表示可以统一采用一般的形式来表示，称为Cohen类时频分布，统一表述如下[10]：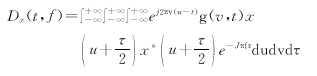
(4)
, http://www.100md.com
其中，x(t)为分析的信号，g(v,t)为核平滑函数，它定义了所选择的观测模式。
该统一的时—频表述可以提供一个许多时频分析方法的通用工具，并且满足一些必要的性质：(1)时频分布对时间和频率的积分给出信号的能量，对时间的积分给出信号的谱密度，对频率的积分给出信号的瞬时功率；(2)时频分布的一阶矩给出瞬时频率和信号的群延时，这些性质对核平滑函数提出了一定的要求，从而使实际应用的时频表示是上述情形的一个子集合；较广泛具有上述特性的表示有：Cohen分布类，Wigner—Ville分布类，Rihaczek分布类，Choi—Williams分布类共四类。Wigner—ville可以采用下面的表达式：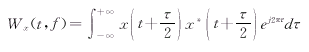
(5)
Wigner—Ville 分布的时间频率分辨率较好，具有一定的物理意义，但是，在该分布中存在着严重的交叉项干扰，使得实际应用受到很大限制，实际应用中广泛采用的时—频表示就是STFT构成的谱图和最近发展起来的小波尺度图，这两个时—频表示有人研究表明都是Wigner—Ville分布的一种变形[5]，STFT构成的谱图是消除了交叉项的伪Wigner—Ville分布，小波尺度谱则是一类仿射平滑的Wigner—Ville分布，其中关键是采用时间和频率分离的核平滑函数。在实际应用中我们利用文献[9]中的平滑函数：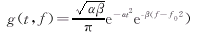
(6)
, 百拇医药
其中，α，β，f0均为正的常数。该核平滑函数由于采用了高斯型结构，使得分析平滑结果在一定意义上是最优的，既有较好的平滑结果，又有较好的时频分辨率[9]。
(7)
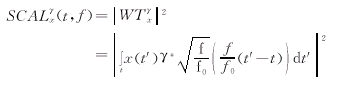(8)
采用上面的平滑函数并结合谱图的定义式(8)与小波尺度图的定义式(9)我们就可以进行小波尺度图和谱图的实际计算，具体计算方法参看后面的仿真结果。
超声血流多普勒信号的小波尺度图方法的应用与讨论
理论研究表明Doppler信号是人体中许多超声散射体对超声的背向散射而形成的，背向散射体的主要成分是红细胞，在血流是稳定层流的情形下，该信号的功率谱特性与流速抛面的形式有一定的关系，其关系可以用下式来表示[7]：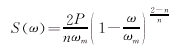
(9)
, http://www.100md.com
其中，ωm是Doppler最大频率，n是流速抛面参数；在一个心动周期中，实际的血流速度是变化的，心脏收缩射血期的血流速度较大，流速抛面参数较小，流速抛面的纵端面形状是抛物线形状，而在心脏舒张末期的血流速度较慢，流速抛面参数较大，流速抛面的纵端面形状是椭圆形状，具体的正常人体的颈总动脉血流的平均频率曲线已经有人进行了测量和分析[6]，基本波形如图1所示。
从血流谱密度的表达式(9)和从血流多普勒信号的平均频率曲线可以看出，Doppler信号必然是一个非平稳的信号。此外，当人体的某一部位发生病变时，在此部位的血管和血流情况必然要受到影响，由于病变引起了血管局部狭窄，从而出现血流的湍流和紊流，这些湍流和紊流的可以使Doppler信号产生非正常的变化，理论分析表明，湍流和紊流可以使Doppler信号的平均频率曲线上出现非正常畸变，也可以使Doppler信号的频谱带宽增大[8]，从而使Doppler信号的非平稳性更加增大，这也是在实际应用中造成Doppler信号非平稳的一个很重要的原因，综合起来看，实际的Doppler信号是一个非平稳信号，非平稳性是它的一个基本特性，无论从人体血流的心动周期的变化，还是从人体某部位病变区域的血流变化，都可以得出超声信号的非平稳性特点，如何从理论和实际的测量数据来仿血流Doppler信号就是一个很基本的思想，根据文献[8]中的方法，采用“平均频率反推法”，我们进行了人体颈总动脉的血流多普勒信号仿真，在仿真时设实际信号的采样频率为14 kHz，为了方便起见，信号带宽设为常数等于100Hz，仿真数据长度为一个心动周期，(取为0.96 s，即心律约为63次/min)；并且在实际应用中采用的平均频率曲线是图(1)所示的曲线；对于具有某中病理特性的信号，其平均频率曲线可以从实际的有关临床医学中进行测量获得，本文所有的仿真程序都是用MATLAB语言在PC机上实现的。具体的仿真结果见图2所示。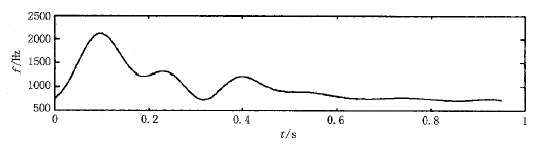
, 百拇医药
图1 正常人颈总动脉血流Doppler信号的平均频率曲线
Fig.1 Mean frequency waveform of the normal human common carotid arterial Doppler signal
图2 正常人体颈总动脉血流多普勒信号仿真结果
Fig.2 Simulation of normal human common carotid arterial arterial Doppler signal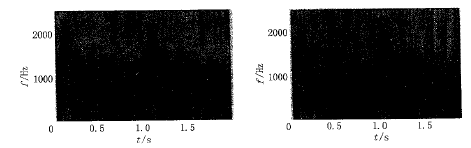
图3 颈总动脉多普勒血流信号的短时傅立叶变换谱图(a)和小波尺度图(b)
, 百拇医药
Fig.3 STFT spectrum and wavelet scalogram of the neck artery blood Doppler signal
从而，对仿真信号我们进行了谱图和尺度图的计算研究，实际谱图和尺度图的离散计算方法，可以参看文献[10]，在此不做详细分析，实际计算中为了防止信号谱的泄漏，以及考虑到信号的平稳性假设[8]，谱图计算采用了10 ms的海明窗进行加权，尺度图则采用了100 ms的矩形窗，而且为了分析和讨论的准确性，我们采用了两个心动周期仿真数据进行研究，对于实际仿真的两个心动周期Doppler信号进行分析后得到了医学上的声谱图和小波尺度图，见图(3)所示。图中(a)是STFT谱图，(b)是小波尺度图，灰度表示信号频谱的幅值大小，而且尺度图采用了将尺度进行取倒数的方式进行显示，从中可以看出小波尺度图对高频部分的分辨率较STFT谱图好，但是信号的交叉项干扰较大些。
综合上面的分析和仿真结果可以看出，对于Doppler信号的谱估计问题，采用小波分析的方法来处理，并得到关于信号的时-频分布的尺度图(scale—gram)较短时Fourier变换的低频特性好，这可能是由于小波的时窗和频窗的宽度是可变的，这种可变的时间频率窗对于本质非平稳多普勒信号分析更为合适，特别是在分析信号的低频段时，小波分析的窗函数能够取得较长，使得信号的低频分辨率比谱图好，但是由于时间窗较长也使得信号的非平稳性特点变的更剧烈，核平滑函数的平滑性能相对较弱，交叉项干扰就比谱图大，该缺点可以采用选择更合适的核平滑函数来解决。
, 百拇医药
结 论
理论分析和仿真结果表明，对于非平稳超声血流多普勒信号的谱估计问题，由于付立叶变换的平稳性假设，使得对于实际本质非平稳信号的付立叶变换存在原理上的问题，小波变换的尺度图具有较好的低频特性，从而可以提高小血管中中低速血流的估计精度。但是由于是一类仿射平滑的Wigner-Ville变换，在消除交叉干扰项的能力上较谱图差，有必要进一步寻找较好的仿射平滑函数。
[参考文献]
[1] XU Jingping,WU Yanjun,CHENG Jangzhi et al.Generalized time-frequency analysis of biomedical signals[J].Journal of Biomedical Engineering,1996,13(1):68～74
徐泾平，吴延军,陈江之等.生物医学信号的广义时频分析[J].生物医学工程学杂志,1996,13(1):68～74
, http://www.100md.com
[2] Quistgaard JU.Signal acquistion and processing in medical diagnostic ultrasound[J].IEEE. Singnal and Processing Magazine，1997,32(1):67～74
[3] PU Junxiang,ZHANG Lifan,SHANG Junhua et al.Echo cardiographic assessment of left venticular structure and function after simulated weight-lessness in rats[J] Space Medicinve & Medical Engineering,1999,12(2):88～91
暴军香，张立藩，商慧华等. 超声心动图监测模拟失重大鼠左心室的结构与功能[J].航天医学与医学工程，1999，12(2)：88～91
, 百拇医药
[4] HUAN Fei,ZHENG Chongxun,HUANG Yungui.Detection of spikes in epiletptic EEG by using wavelet series[J].Space Medicinve & Medical Engineering,1999,12(3):200～203
宦 飞，郑崇勋，黄运桂. 利用小波级数监测癫痫EEG中的棘波[J].航天医学与医学工程，1999，12(3)：200～203
[5] Routh HF.Dopple Ultrasound the ability to measure and image blood flow[J].IEEE. Signal and Processing Magazine,1996,31(1):31～40
[6] Cardoso JCS,Ruano MJ,Peter J. Fish nonstationarity broadening reduction in pulsed Doppler spectrum measurements using time-frequency estimators[J].IEEE Trans BME, 1996,43(12):1176～1182
, 百拇医药
[7] Flandrin OP.Time-scale distribution:A general class extending wavelet transforms[J].IEEE Trans SP，1992,40(7):1746～1757
[8] Leon Cohen.Time-frequency distribution a review[J].IEEE Proceeding,1989,77(7) :941～981
[9] Unser M,Aldroubi A.A review of wavelets in biomedical application[J]. IEEE Proceeding,1996,84(4):626～639
[10] Nikolaj Hess-Nielsen,Wickerhauser MV.Wavelets and time-frequency analysis[J].IEEE Proceeding,1996,84(4):523～539
收稿日期：1999-07-28, 百拇医药
单位：张平(中国航天科技集团公司704所，北京 100076)；刘颖(哈尔滨市第一医院内分泌科，哈尔滨 150010)；刘志言 沈毅(哈尔滨工业大学控制工程系，哈尔滨 150001)；于建宏(中国人民解放军211医院，哈尔滨 150000)
关键词：小波变换；付里叶变换；多普勒信号；血流；频谱分析
航天医学与医学工程000209摘要： 目的 将现代小波尺度图分析方法应用到人体血流多普勒信号的谱估计之中，计算血流多普勒信号的功率谱，得到小波意义上的尺度图。 方法 从时频分布的观点，小波尺度图是一种仿射平滑的Wigner-Ville分布，具有恒“Q”特性的时间频率分析窗，对于人体颈总动脉的仿真多普勒血流信号，进行了小波尺度图的研究。 结果 通过血流多普勒信号的小波尺度图研究，发现利用小波尺度图可以提高血流多普勒信号低频段的频谱分辨率。 结论 利用小波方法估计人体血流多普勒信号的频谱特性是可行的，估计结果的低频段频谱的分辨率较高，从而可以提高小血管中低速血流的估计精度。
, http://www.100md.com
中图法分类号：R319；R540.4 文献标识码：A 文章编号：1002-0837(2000)02-0119-05
Analysis of Wavelet Scalogram of Blood Flow Ultrasonic Doppler Signal.
ZHANG Ping,LIU Ying,LIU Zhi-yan，SHEN Yi,YU Jian-hong.
Abstract: Objective To study the power spectrum density of blood flow ultrasonic Doppler signal using wavelet analysis. Method Doppler signal of blood flow in human common carotid artery was studied with wavelet scalogram analysis, an affine smoothing Wigner-Ville transform with a constant “Q" character. Result Wavelet scalogram of blood flow ultrasonic signal had a higher distinguishability than STFT spectrogram in the low frequency portion, but had poorer decussation terms than spectrogram. Conclusion It is practicable to estimate the spectrum of Doppler signals of blood flow by the wavelet analysis method. And this can be used in low speed blood flow for higher resolution of spectrum in the low frequency portion.
, 百拇医药
Key words:wavelet transform;fourier transform;doppler signal;blood flow;spectrum analysis
对于平稳信号的处理工具仍然是Fourier变换，但是，在实际应用中的绝大多数信号是非平稳的，现在看来处理非平稳信号的主要工具将是小波变换，这主要是因为传统的Fourier变换分析信号时，时间和频率分辨率精度是固定不变的，而利用小波变换分析信号，在信号高频段时间分辨率精度也较高，在信号低频段频率分辨率精度较高，这很符合非平稳信号的特点。因此利用小波变换进行非平稳信号的分析可以得到较好的时间和频率估计精度[1]。超声多普勒血流信号的分析技术由于能可靠而灵敏地用于血管疾病的诊断，逐渐成为临床医学的一种重要诊断手段，尤其在心血管疾病的研究及临床诊断中有重要的意义，采用声谱图进行血流状态的分析更是受到普遍的承认，这主要是因为多普勒回波信号的动态功率谱中包含了血流的速度、方向等多方面的信息[2]。但是，采用小波尺度图来讨论分析医疗超声血流多普勒信号的谱特性还没有人研究[3，4]，本文旨在采用小波变换来进行信号的谱特性分析，同时对信号的功率谱特性进行比较，得到一些有意义的结果。
, http://www.100md.com
小波变换(WT)的恒“Q”特性时间—频率窗
古典Fourier分析是对所有时间的积分得到，只能获得整个信号的频谱，不能得到信号在某一时间段上的频率特性。从时频分布的观点来看，其频域的分辨率为最高(可以定义到某一根谱线)，但其时域分辨率为无穷小(即变换后不能提供任何时域中的信息)。鉴于以上原因，Gabor在1948年提出了加窗的短时付立叶变换思想，它在付立叶变换的基础上引入了一个时间域内局部化的“窗函数”，通过以上的方法虽然可以得到某一时间段内的频率特性，但还是存在如下的缺点：窗函数的宽度固定不变，其时域和频域的分辨率是固定不变的，不能满足一般情况下的需要，即：在信号的高频段时间窗应该短些，以利于观察信号的剧烈变化，而在低频率段时间窗要宽一些，以利于看到信号的全貌和更精细的频率信息。小波分析从根本上解决了上述缺点，使其有很大的应用灵活性和广泛性，如果定义一个函数h(t)且有：∫|th(t)|2dt<+∞,h∈L2(R)，，则称该函数为一个窗函数，且该函数的窗中心和窗半径分别由下式来确定：
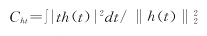(1) (2), 百拇医药
数值
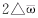就是窗函数的宽度，同样，如果窗函数的Fourier变换也满足窗函数的条件，即：H(ω)=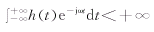一个实际信号在该窗函数作用下进行的Fourier变换就表明了信号在如下窗内的信息: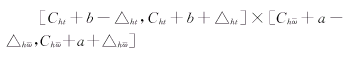其中，a,b分别为信号在时域内和频域内的中心，而关于f∈L2(R)的连续小波变换定义为：
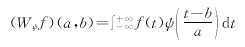(3)其中，ψ(t)∈L2(R),并满足容许条件，
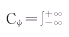
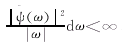,则称ψ为一个小波母函数或基小波，对于小波的一个重要性质是小波函数是一个窗函数，其时间窗和频率窗分别为: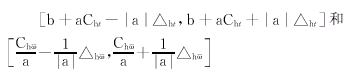, 百拇医药
其中，a是小波变换的尺度，b是小波变换在时间轴上的时间值。从上面的式子可以看出，窗的形状随着参数a的变化而变化，b变大，时间窗增大，频率窗变小，小波对应的频率成分也变小，适合分析低频信号；反之，b变小，时间窗增小，频率窗变大，小波对应的频率成分也变高，则适合分析高频信号，这就是小波分析较短时Fourier变换优越的特点。
尺度图的时间—频率分析特性研究
随着对非平稳信号处理研究的深入，现代时间-频率分析技术得到广泛的研究和应用，谱图和尺度图是时间频率分析中二次型时频表示中的最简单的两种情况，谱图可以看成是一组带通滤波器带宽与分析频率无关的一类分析滤波器输出幅值的平方，而尺度图则是采用滤波器的带宽与分析的频率成正比的一类分析滤波器输出幅值的平方，可以看成为一类“恒Q”形式的谱图。
对于能量型的二次时频表示可以统一采用一般的形式来表示，称为Cohen类时频分布，统一表述如下[10]：
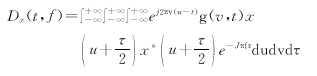(4), http://www.100md.com
其中，x(t)为分析的信号，g(v,t)为核平滑函数，它定义了所选择的观测模式。
该统一的时—频表述可以提供一个许多时频分析方法的通用工具，并且满足一些必要的性质：(1)时频分布对时间和频率的积分给出信号的能量，对时间的积分给出信号的谱密度，对频率的积分给出信号的瞬时功率；(2)时频分布的一阶矩给出瞬时频率和信号的群延时，这些性质对核平滑函数提出了一定的要求，从而使实际应用的时频表示是上述情形的一个子集合；较广泛具有上述特性的表示有：Cohen分布类，Wigner—Ville分布类，Rihaczek分布类，Choi—Williams分布类共四类。Wigner—ville可以采用下面的表达式：
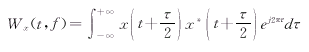(5)Wigner—Ville 分布的时间频率分辨率较好，具有一定的物理意义，但是，在该分布中存在着严重的交叉项干扰，使得实际应用受到很大限制，实际应用中广泛采用的时—频表示就是STFT构成的谱图和最近发展起来的小波尺度图，这两个时—频表示有人研究表明都是Wigner—Ville分布的一种变形[5]，STFT构成的谱图是消除了交叉项的伪Wigner—Ville分布，小波尺度谱则是一类仿射平滑的Wigner—Ville分布，其中关键是采用时间和频率分离的核平滑函数。在实际应用中我们利用文献[9]中的平滑函数：
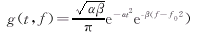(6), 百拇医药
其中，α，β，f0均为正的常数。该核平滑函数由于采用了高斯型结构，使得分析平滑结果在一定意义上是最优的，既有较好的平滑结果，又有较好的时频分辨率[9]。
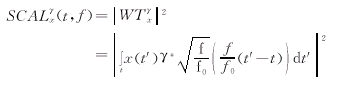(7) (8)采用上面的平滑函数并结合谱图的定义式(8)与小波尺度图的定义式(9)我们就可以进行小波尺度图和谱图的实际计算，具体计算方法参看后面的仿真结果。
超声血流多普勒信号的小波尺度图方法的应用与讨论
理论研究表明Doppler信号是人体中许多超声散射体对超声的背向散射而形成的，背向散射体的主要成分是红细胞，在血流是稳定层流的情形下，该信号的功率谱特性与流速抛面的形式有一定的关系，其关系可以用下式来表示[7]：
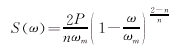(9), http://www.100md.com
其中，ωm是Doppler最大频率，n是流速抛面参数；在一个心动周期中，实际的血流速度是变化的，心脏收缩射血期的血流速度较大，流速抛面参数较小，流速抛面的纵端面形状是抛物线形状，而在心脏舒张末期的血流速度较慢，流速抛面参数较大，流速抛面的纵端面形状是椭圆形状，具体的正常人体的颈总动脉血流的平均频率曲线已经有人进行了测量和分析[6]，基本波形如图1所示。
从血流谱密度的表达式(9)和从血流多普勒信号的平均频率曲线可以看出，Doppler信号必然是一个非平稳的信号。此外，当人体的某一部位发生病变时，在此部位的血管和血流情况必然要受到影响，由于病变引起了血管局部狭窄，从而出现血流的湍流和紊流，这些湍流和紊流的可以使Doppler信号产生非正常的变化，理论分析表明，湍流和紊流可以使Doppler信号的平均频率曲线上出现非正常畸变，也可以使Doppler信号的频谱带宽增大[8]，从而使Doppler信号的非平稳性更加增大，这也是在实际应用中造成Doppler信号非平稳的一个很重要的原因，综合起来看，实际的Doppler信号是一个非平稳信号，非平稳性是它的一个基本特性，无论从人体血流的心动周期的变化，还是从人体某部位病变区域的血流变化，都可以得出超声信号的非平稳性特点，如何从理论和实际的测量数据来仿血流Doppler信号就是一个很基本的思想，根据文献[8]中的方法，采用“平均频率反推法”，我们进行了人体颈总动脉的血流多普勒信号仿真，在仿真时设实际信号的采样频率为14 kHz，为了方便起见，信号带宽设为常数等于100Hz，仿真数据长度为一个心动周期，(取为0.96 s，即心律约为63次/min)；并且在实际应用中采用的平均频率曲线是图(1)所示的曲线；对于具有某中病理特性的信号，其平均频率曲线可以从实际的有关临床医学中进行测量获得，本文所有的仿真程序都是用MATLAB语言在PC机上实现的。具体的仿真结果见图2所示。
, 百拇医药
图1 正常人颈总动脉血流Doppler信号的平均频率曲线
Fig.1 Mean frequency waveform of the normal human common carotid arterial Doppler signal
图2 正常人体颈总动脉血流多普勒信号仿真结果
Fig.2 Simulation of normal human common carotid arterial arterial Doppler signal
图3 颈总动脉多普勒血流信号的短时傅立叶变换谱图(a)和小波尺度图(b)
, 百拇医药
Fig.3 STFT spectrum and wavelet scalogram of the neck artery blood Doppler signal
从而，对仿真信号我们进行了谱图和尺度图的计算研究，实际谱图和尺度图的离散计算方法，可以参看文献[10]，在此不做详细分析，实际计算中为了防止信号谱的泄漏，以及考虑到信号的平稳性假设[8]，谱图计算采用了10 ms的海明窗进行加权，尺度图则采用了100 ms的矩形窗，而且为了分析和讨论的准确性，我们采用了两个心动周期仿真数据进行研究，对于实际仿真的两个心动周期Doppler信号进行分析后得到了医学上的声谱图和小波尺度图，见图(3)所示。图中(a)是STFT谱图，(b)是小波尺度图，灰度表示信号频谱的幅值大小，而且尺度图采用了将尺度进行取倒数的方式进行显示，从中可以看出小波尺度图对高频部分的分辨率较STFT谱图好，但是信号的交叉项干扰较大些。
综合上面的分析和仿真结果可以看出，对于Doppler信号的谱估计问题，采用小波分析的方法来处理，并得到关于信号的时-频分布的尺度图(scale—gram)较短时Fourier变换的低频特性好，这可能是由于小波的时窗和频窗的宽度是可变的，这种可变的时间频率窗对于本质非平稳多普勒信号分析更为合适，特别是在分析信号的低频段时，小波分析的窗函数能够取得较长，使得信号的低频分辨率比谱图好，但是由于时间窗较长也使得信号的非平稳性特点变的更剧烈，核平滑函数的平滑性能相对较弱，交叉项干扰就比谱图大，该缺点可以采用选择更合适的核平滑函数来解决。
, 百拇医药
结 论
理论分析和仿真结果表明，对于非平稳超声血流多普勒信号的谱估计问题，由于付立叶变换的平稳性假设，使得对于实际本质非平稳信号的付立叶变换存在原理上的问题，小波变换的尺度图具有较好的低频特性，从而可以提高小血管中中低速血流的估计精度。但是由于是一类仿射平滑的Wigner-Ville变换，在消除交叉干扰项的能力上较谱图差，有必要进一步寻找较好的仿射平滑函数。
[参考文献]
[1] XU Jingping,WU Yanjun,CHENG Jangzhi et al.Generalized time-frequency analysis of biomedical signals[J].Journal of Biomedical Engineering,1996,13(1):68～74
徐泾平，吴延军,陈江之等.生物医学信号的广义时频分析[J].生物医学工程学杂志,1996,13(1):68～74
, http://www.100md.com
[2] Quistgaard JU.Signal acquistion and processing in medical diagnostic ultrasound[J].IEEE. Singnal and Processing Magazine，1997,32(1):67～74
[3] PU Junxiang,ZHANG Lifan,SHANG Junhua et al.Echo cardiographic assessment of left venticular structure and function after simulated weight-lessness in rats[J] Space Medicinve & Medical Engineering,1999,12(2):88～91
暴军香，张立藩，商慧华等. 超声心动图监测模拟失重大鼠左心室的结构与功能[J].航天医学与医学工程，1999，12(2)：88～91
, 百拇医药
[4] HUAN Fei,ZHENG Chongxun,HUANG Yungui.Detection of spikes in epiletptic EEG by using wavelet series[J].Space Medicinve & Medical Engineering,1999,12(3):200～203
宦 飞，郑崇勋，黄运桂. 利用小波级数监测癫痫EEG中的棘波[J].航天医学与医学工程，1999，12(3)：200～203
[5] Routh HF.Dopple Ultrasound the ability to measure and image blood flow[J].IEEE. Signal and Processing Magazine,1996,31(1):31～40
[6] Cardoso JCS,Ruano MJ,Peter J. Fish nonstationarity broadening reduction in pulsed Doppler spectrum measurements using time-frequency estimators[J].IEEE Trans BME, 1996,43(12):1176～1182
, 百拇医药
[7] Flandrin OP.Time-scale distribution:A general class extending wavelet transforms[J].IEEE Trans SP，1992,40(7):1746～1757
[8] Leon Cohen.Time-frequency distribution a review[J].IEEE Proceeding,1989,77(7) :941～981
[9] Unser M,Aldroubi A.A review of wavelets in biomedical application[J]. IEEE Proceeding,1996,84(4):626～639
[10] Nikolaj Hess-Nielsen,Wickerhauser MV.Wavelets and time-frequency analysis[J].IEEE Proceeding,1996,84(4):523～539
收稿日期：1999-07-28, 百拇医药