地面传热实验的微重力修正模拟
作者:姬朝玥 任建勋 梁新刚 陈泽敬 徐向华 过增元
单位:清华大学工程力学系,北京 100084
关键词:航天器;微重力修正;数值模拟;地面试验;等壁热;等热流;对流传热
航天医学与医学工程000411摘要: 目的 使空间飞行器地面传热实验的结果能够有效地应用到空间微重力条件下。 方法 用数值模拟的方法研究了矩形空间内45°对称间隔斜进风以及垂直进风的流动和换热情况,壁面条件为等壁温或等热流。对重力和微重力两种情况进行了对比。 结果 对等壁温情况,提出了表征空间飞行器舱内换热的关系式,并且将数值计算所得数据按这些关系式进行了最小二乘拟合,得到了空间微重力工况和地面工况下的换热关系式。对等热流情况,本文列出了重力和微重力条件下的最高壁面温度值,给出了两种情况时最高壁面温度的拟合公式。 结论 根据本文的方法,可以对地面模型装置的实验结果进行修正,得到空间飞行器原型内的换热情况。
, 百拇医药
中图分类号:R852.82 文献标识码:A 文章编号:1002-0837(2000)04-0281-05
Numerical Correlation of Convections in an Enclosure under Micro-gravity and terrestrial Gravity
JI Chao-yue REN Jian-xun LIANG Xin-gang CHEN Ze-jing XU Xiang-hua GUO Zeng-yuan
(JI Chao-yue.Department of Engineering Mechanics, Tsinghua University, Beijing 100084, China)
Abstracts: Objective To apply the ground-based heat transfer experimental results to the spacecraft in micro-gravity. Method The flow and heat transfer characteristics in a square cavity were investigated numerically, for a symmetric interval 45°oblique air inlet pattern and vertical air inlet pattern, with boundary conditions of uniform temperature and uniform heat flux at vertical walls. The results in conditions of gravity and micro-gravity were compared. Result First, the heat transfer correlation formula in spacecraft were presented under the condition of uniform wall temperature. Second, the data of numerical simulation were fitted with the Least Square Method. And the correlation for cases under gravity and micro-gravity were obtained. Finally, for the boundary condition of uniform heat flux, the fitting equations of maximum wall temperature in the condition of gravity and micro-gravity were given and the values of maximum wall temperature were listed in a table. Conclusion The heat transfer characteristics in the spacecraft under micro-gravity can be predicted from those correlation obtained from ground-based results.
, 百拇医药
Key words:space vehicles;micro-gravity modification;numerical simulation;ground tests;uniform wall temperature;uniform heat flux;covective heat transfer
为了给空间飞行器热设计提供依据,考核热控系统的适应能力以及确定最佳热控参数,必须在研制过程中进行充分的地面模拟实验。如前苏联的“联盟号”飞船,就曾建立了相应的大型空间模拟设备,进行过多次地面模拟实验。
由于地面有重力作用,当有温差存在时,地面模型的对流换热状况会与空间环境不同,造成地面实验的结果和空间微重力实际情况有一定偏差。为此,前人曾采用实验的方法来获得微重力环境,如落塔、落井、飞机、火箭等实验,但用这些方法获得的工作时间太短,无法满足实验的热稳定性要求。为了在地面模拟微重力环境下舱内的流动和换热,并保持模型的温度和材料与原型一致,必须保持Re数(Re为雷诺数,定义为Re=ρuL/μ,其中ρ为流体密度,μ为特征速度,L为特征尺度,μ为流体的动力粘性系数)相同,并尽可能地减小格拉晓夫数Gr,以抑制自然对流的影响。由Gr数的表达式Gr=ρ2gβL3T0/μ2可知,若使重力加速度g、气体膨胀系数β、参考温度T0和动力粘度μ保持不变,则减小Gr数可以通过改变密度ρ和尺寸L来实现,这样就产生了两种Gr数调整技术,即缩小尺寸的保持技术和改变压力的保持技术。这两种方法通常称为缩比法[1]和减压法。文献[2]研究了对流换热的地面相似模拟技术,提出了抑制自然对流的温度-材料-Nu数综合保持技术,即通过按比例缩小尺寸,降低Gr数,保持材料和Re数不变的办法,使自然对流的作用减弱到可以忽略的程度,从而实现模型与原型的流场和温度场的相似,实现在地面模拟微重力条件下的流动和换热。该方法的关键是使Gr/Re2小于某一临界值,使在地面时自然对流的影响可以忽略。文献[2]的作者进一步提出了地面模拟传质的技术[3]。前苏联采用过减压法进行地面模拟实验。但减压法最大的缺点是无法模拟有传质的问题[4]。这是由于饱和湿度和湿扩散系数随压力的变化很大,无法保持湿度。缩比法虽然能较好地模拟空间飞行器的流动、传热和传质,但因为空间飞行器是个非常复杂的系统,保持缩比模型和原型的完全相似很困难。所以,为了对空间飞行器的热设计提供可靠的参考,需要进行地面1∶1模型的实验,以至初样、正样实验,这是缩比法和减压法不能替代的。而如前所述,地面实验中重力的影响是无法避免的,因此,如果能把地面1∶1模型的实验结果经过某种修正,得到和微重力条件下原型比较吻合的结果,就可以通过地面直接模拟来指导空间飞行器的热设计了。本文就试图提出一种地面实验结果的修正方法。
, 百拇医药
物理数学模型
根据空间飞行器的几何结构,可将其简化为方腔来研究其中的流动和传热问题。本文研究了两种进风方式的方腔内的传热问题。第一种进风方式是45°对称间隔斜进风,如图1所示,以y轴为对称轴,两边对称,每边分成6段,其中的3段斜进风口彼此间隔开来。第二种进风方式是垂直进风,如图2所示。图1和图2中的方腔总体几何尺寸及出风方式是一样的。采用45°对称间隔斜进风方式和垂直进风方式,有利于空间飞行器舱内的通风、换热,有利于舱内空气的速度、温度、湿度均匀分布,有利于舱内空气流动稳定,以及满足舒适性的要求。从这些方面考虑,这两种进风方式,尤其是45°对称间隔斜进风方式,比均匀进风方式、小孔垂直进风方式及其它形式的斜进风方式要好一些[5]。因此,这两种方式也是空间飞行器可能采用的两种进风方式,所以本文以这两种方式为例来给出微重力修正的方法。本文对5种不同流量的工况在重力和微重力条件下这两种进风方式的原型尺寸的方腔内的流动换热情况进行了数值模拟。这5种流量对应的Re数分别为20000、30000、40000、50000、60000。
, 百拇医药
图1 空间飞行器45°间隔斜进风方式示意图
Fig.1 Interval 45°oblique air inlet pattern of spacecraft
图2 空间飞行器垂直进风方式示意图
Fig.2 Vertical air inlet pattern of spacecraft
描述方腔内空气流动和传热特性的基本方程包括连续方程、动量方程和能量方程,它们的无量纲形式分别为: (1)
(1)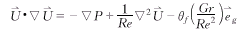 (2)
(2)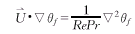 (3)
(3)
, 百拇医药
它们同边界条件一起,构成了舱内空气流动与传热的数学模型。在本文中,对两种进风方式都进行了等壁温边界条件下的计算,对斜进风方式,还计算了等热流边界条件下的情况。无论是等壁温还是等热流边界条件,都是对称地加在图1、图2中与x方向垂直的两个侧壁上,其余壁面均为等壁温边界条件,温度低于这两个侧面。数值模拟采用三维计算,假设方腔内流动为层流,空气物性满足Boussinesq假定。所有工况均采用65×30×85非均匀网格,SIMPLER算法[6]。
等壁温条件下壁面平均Nu数的修正
本文提出的修正公式都是换热方面的,因为流动方面的情况,通过地面的冷态实验,就可以得到和微重力条件下相同的结果。
45°间隔斜进风方式 对流换热系数是空间飞行器热设计所需要的重要参数之一,我们有必要对空间飞行器内空气在壁面的对流换热系数进行认识和研究。对空间飞行器内空气的流动和换热进行数值计算之后,可以得到其中的温度分布。根据这一温度分布,可以求得壁面热流密度qw,其表达式为: (4)
(4)
, 百拇医药
其中,λ是空气的导热系数。壁面温度梯度用3点差分格式求得。有了壁面热流密度,就可以求得对流换热系数α,可由下式求得: (5)
(5)
其中,ΔT=Tw-Tin,是等温加热的壁面和进口之间的温差。由此得努赛尔数Nu: (6)
(6)
在壁面上对Nu数取平均,就得到壁面平均Nu数。壁面平均Nu数反映了空气在空间飞行器内壁面上的对流换热特性。
表1列出了通过数值计算得到的不同Re数时,在重力和微重力两种情况下的壁面平均Nu数。在表1中,下标mg代表微重力情况,以重力加速度g=0.0 m/s2的情况近似[2~5],下标g代表重力情况,重力加速度g=9.8 m/s2。由表1可以看出,地面重力条件下的换热量明显大于空间微重力条件下的换热量。随着Re数的增加,壁面换热量增加。两种情况下壁面平均Nu数的比值在不同Re数时是不同的,随着Re数的增加,这一比值也增加,这表明微重力条件下换热量的增加快于重力条件下。
, 百拇医药
表1 不同Re数,重力、微重力条件下壁面Nu数
Table 1 Nu number in different Re numbers in gravity or micro-gravity condition Re/104
Numg
Nug
2.0
73.52
160.46
0.458
, 百拇医药 3.0
95.47
171.08
0.558
4.0
109.73
176.67
0.621
5.0
122.32
182.17
0.671
6.0
, 百拇医药
136.30
186.24
0.732
根据量纲分析,对受迫对流,有: Nu=f(Re,Pr) (7)
对混合对流,有:
Nu=f(Re,Gr,Pr) (8)
式中,Pr为普朗特数,Pr=μcp/λ,cp为空气的比热,本文中,对空气,Pr=0.71。参考已有的受迫对流、混合对流实验关联式[7],用已定准则幂函数形式整理本文计算所得的数据,设:
Numg=C1Rem1 (9)
, http://www.100md.com
Nug=C2Rem2Grn1 (10)
在两式中,即在微重力原型和地面模型装置中,对固定工况,Re数是保持一致的,则: (11)
(11)
根据经验公式,取n1=1/3[7],在本文中,Gr=2.2×1010。对表1所列数据,由最小二乘法拟合,得C1=0.3182,m1=0.5510,C2=0.01521,m2=0.1342,从而得出C3=20.92,m3=0.4168,n2=-1/3。因此,可分别得到微重力原型和地面1∶1模型装置的壁面Nu数关系式:
, http://www.100md.com
Numg=0.3182Re0.5510 (12)
Nug=0.01521Re0.1342Gr1/3 (13)
由式(12)和式(13)可得及壁面平均Nu数的修正公式: (14)
(14)
表2列出了本文数值模拟的结果和用拟合公式(12)计算所得的结果,以及这两组数据的相对误差ε。可以看出,表2中相对误差的绝对值最大不超过2.34%。用同样的方法计算了拟合公式(13)和(14)的相对误差,其绝对值均在2%以内。可以看出,由拟合公式(12),(13),(14)的计算结果与原始数据符合得很好,这说明拟合公式(12),(13),(14)可以较好地反映45°间隔斜进风时空间飞行器舱内不同工况时的换热规律。这表明我们前述对空间飞行器舱内换热规律的分析和假设是正确的。这样,只要知道1∶1地面模拟时的Re数、Gr数和Nu数,就可以根据(14)式求得
, 百拇医药
表2 数值模拟与式(12)计算所得Nu值比较
Table 2 Comparison between numerical simulation results and calculated values from equation (12) for Nu number Re/104
numerical
simulation results
fitting values
ε
2.0
73.52
74.57
, 百拇医药
1.43%
3.0
95.47
93.24
-2.34%
4.0
109.73
109.25
-0.44%
5.0
122.32
123.55
1.01%
, 百拇医药
6.0
136.30
136.60
0.22%
45°间隔斜进风时在微重力条件下的Nu数,即: Numg=20.92Re0.4168Gr-1/3Nug (15)
垂直进风方式 表3列出了数值模拟的结果。可以看出,所得结论与斜进风基本相同。地面1∶1模型装置的换热量明显大于空间飞行器原型的换热量。相同条件下,壁面换热量随流量的增加而增加,微重力条件下换热量增加快于重力条件下。与表1数据作一对比发现,在垂直进风时,微重力条件下的换热量要大于斜进风时,而在重力条件下换热量则小于斜进风时,因此,在垂直进风时,重力和微重力两种条件下壁面换热量的差别要比斜进风时小,从这个角度来看,垂直进风方式比斜进风方式更容易抑制自然对流的影响,尤其是在Gr数不变而增大Re数的情况下。
, 百拇医药
表3 不同Re数,重力、微重力条件下壁面Nu数
Table 3 Nu number in different Re numbers in gravity or micro-gravity condition Re/104
Numg
Nug
2.0
94.72
155.08
0.611
, 百拇医药 3.0
121.61
166.86
0.729
4.0
143.59
174.87
0.821
5.0
160.76
180.56
0.890
6.0
, 百拇医药
174.34
183.98
0.948
与斜进风方式的整理方法相同,对表3中的数值模拟结果按最小二乘法进行拟合,得到垂直进风等壁温条件下空间飞行器原型和地面1∶1模型装置中壁面换热公式及壁面平均Nu数的修正公式: Numg=0.3784Re0.5590 (16)
Nug=0.01169Re0.1575Gr1/3 (17)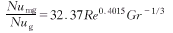 (18)
(18)
式(16),(17),(18)的拟合误差的绝对值不超过2%,表明这3个拟合公式可以基本反映垂直进风时空间飞行器舱内不同工况时的换热规律。类似于公式(15),可得垂直进风时微重力条件下的Nu数的修正公式:
, 百拇医药
Numg=32.37Re0.4015Gr-1/3Nug (19)
壁面平均Nu数的通用修正公式 前面对斜进风和垂直进风两种进风方式时壁面平均Nu数提出了微重力修正公式(14)和(18),比较式(14)和式(18)可以看出,两式中Re数的指数很接近。为了便于应用,可以考虑将这两个公式合并。取两个公式中Re数指数的算术平均值作为新的合并公式中Re数的指数,并对公式的系数进行调整,可以将式(14)和式(18)合并为: (20)
(20)
式中,斜进风时,C=22.68;直进风时,C=29.77。简单计算表明,式(20)的拟合误差的绝对值小于2%,说明此式对原始数据拟合得很好。
由此可得等壁温微重力条件下方腔壁面的Nu数的通用修正公式为:
, http://www.100md.com
Numg=CRe0.4092Gr-1/3Nug (21)
其中,常系数C随进风方式的不同而不同。
等热流条件下最高壁温的修正
在空间飞行器的热设计中,最高壁面温度也是我们所关心的一个重要参数。壁面温度如果过高,可导致仪器设备过热损坏。所以有必要对最高壁面温度进行实验预测,从而找出避免壁面温度过高的方法。
本文对某一热流密度条件下45°间隔斜进风的流动换热进行了数值模拟。表4列出了数值模拟所得到的不同工况时的壁面最高温度。可以看出,空间飞行器原型舱中的最高壁面温度要明显高于地面1∶1模型装置中的最高壁面温度。在重力和微重力两种条件下,随着流量的增加,最高壁面温度均有所下降。重力条件下,当Re数大于30000时,下降的幅度很小,最高壁面温度几乎维持不变。
, 百拇医药
表4 不同Re数,重力、微重力条件下最高壁面温度Tmax
Table 4 Maximum wall temperatures in different Re numbers in gravity or micro-gravity condition Re/104
Tmax,mg(℃)
Tmax,g(℃)
2.0
61.92
30.60
3.0
54.90
, 百拇医药
25.15
4.0
45.60
25.38
5.0
41.01
25.13
6.0
35.42
24.83
为了整理出最高壁面温度的微重力修正公式,以便于应用,对表4中的数据按指数函数形式进行最小二乘拟合,可得: Tmax,mg=9820.62Re-0.5079 (22)
, 百拇医药
Tmax,g=156.15Re-0.1698 (23)
两式的拟合误差的绝对值最大不超过7.81%,说明这两个拟合公式可以基本反映重力和微重力条件下最高壁面温度的变化情况。将式(22)和式(23)相除,得: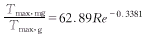 (24)
(24)
由此可得等热流条件下最高壁面温度的修正公式:
Tmax,g=62.89Re-0.3381Tmax,g (25)
根据地面测得的1∶1模型的最高壁面温度及Re数,就可由式(25)求得微重力原型的最高壁面温度,从而达到对地面模型装置实验结果进行修正的目的。
, 百拇医药
结 论
本文数值计算结果表明,空间飞行器在地面的换热特性与微重力条件下有明显差别,地面的实验结果无法直接应用于微重力条件下的空间飞行器,必须经过某种修正,才能对空间飞行器的热设计提供参考依据。本文对等壁温条件下45°间隔斜进风和垂直进风的工况分别提出了修正结果和修正公式(14)、(18),并将两个修正公式合并为一个更为通用的形式;对等热流条件下45°间隔斜进风的最高壁面温度列出了修正结果和修正公式(25)。根据这些公式,可以对地面模型装置实验得到的换热特性进行修正,从而得到微重力条件下空间飞行器舱内的换热特性。
本文研究表明,随着数值计算水平的不断提高,可以提出更完善、齐备的微重力修正公式,从而更好地指导空间飞行器的热设计。实际中空间飞行器的结构是多种多样的。在实际应用中,应结合空间飞行器的具体结构和边界条件进行具体研究。本文给出的是一种方法和思路,可以对实际空间飞行器的热设计提供参考。
, 百拇医药
[参考文献]
[1] Shannon RL. Thermal scale modeling radiation-conduction-convection systems[J].Journal of Spacecraft and Rocket,1973,10(8): 485~491
[2] Liang XG, Guo ZY,Liu YL et al.Ground simulation of flow and heat transfer under micro-gravity[J].Science in China(Series A),1997,40(11): 1204~1209
[3] Liu YL,Liang XG, Ren JX et al.Ground thermal scale modeling of radiation-convective heat and mass transfer system in microgravity environment[J].Chinese Space Science and Technology,1997,27(2): 8~15
, 百拇医药
刘云龙,梁新刚,任建勋等.微重力场中对流-辐射-传质系统的地面模拟技术[J].中国空间科学技术,1997,27(2): 8~15
[4] Liu YL,Ren JX,Liang XG.Grashof number adjustment technique to suppress natural convection[J].Journal of Tsinghua University,1998,38(10): 116~118
刘云龙,任建勋,梁新刚.抑制自然对流的Gr数调整技术[J].清华大学学报,1998,38(10): 116~118
[5] 吴群刚.空间站载人舱简化结构内通风换热的数值研究[D].硕士学位论文,清华大学力学系,1999: 40~90
[6] S.V. 帕坦卡.传热与流体流动的数值计算[M].北京:科学出版社,1992: 153~157
[7] 杨世铭.传热学[M].北京:高等教育出版社,1989:184~224
收稿日期:1999-10-12, 百拇医药
单位:清华大学工程力学系,北京 100084
关键词:航天器;微重力修正;数值模拟;地面试验;等壁热;等热流;对流传热
航天医学与医学工程000411摘要: 目的 使空间飞行器地面传热实验的结果能够有效地应用到空间微重力条件下。 方法 用数值模拟的方法研究了矩形空间内45°对称间隔斜进风以及垂直进风的流动和换热情况,壁面条件为等壁温或等热流。对重力和微重力两种情况进行了对比。 结果 对等壁温情况,提出了表征空间飞行器舱内换热的关系式,并且将数值计算所得数据按这些关系式进行了最小二乘拟合,得到了空间微重力工况和地面工况下的换热关系式。对等热流情况,本文列出了重力和微重力条件下的最高壁面温度值,给出了两种情况时最高壁面温度的拟合公式。 结论 根据本文的方法,可以对地面模型装置的实验结果进行修正,得到空间飞行器原型内的换热情况。
, 百拇医药
中图分类号:R852.82 文献标识码:A 文章编号:1002-0837(2000)04-0281-05
Numerical Correlation of Convections in an Enclosure under Micro-gravity and terrestrial Gravity
JI Chao-yue REN Jian-xun LIANG Xin-gang CHEN Ze-jing XU Xiang-hua GUO Zeng-yuan
(JI Chao-yue.Department of Engineering Mechanics, Tsinghua University, Beijing 100084, China)
Abstracts: Objective To apply the ground-based heat transfer experimental results to the spacecraft in micro-gravity. Method The flow and heat transfer characteristics in a square cavity were investigated numerically, for a symmetric interval 45°oblique air inlet pattern and vertical air inlet pattern, with boundary conditions of uniform temperature and uniform heat flux at vertical walls. The results in conditions of gravity and micro-gravity were compared. Result First, the heat transfer correlation formula in spacecraft were presented under the condition of uniform wall temperature. Second, the data of numerical simulation were fitted with the Least Square Method. And the correlation for cases under gravity and micro-gravity were obtained. Finally, for the boundary condition of uniform heat flux, the fitting equations of maximum wall temperature in the condition of gravity and micro-gravity were given and the values of maximum wall temperature were listed in a table. Conclusion The heat transfer characteristics in the spacecraft under micro-gravity can be predicted from those correlation obtained from ground-based results.
, 百拇医药
Key words:space vehicles;micro-gravity modification;numerical simulation;ground tests;uniform wall temperature;uniform heat flux;covective heat transfer
为了给空间飞行器热设计提供依据,考核热控系统的适应能力以及确定最佳热控参数,必须在研制过程中进行充分的地面模拟实验。如前苏联的“联盟号”飞船,就曾建立了相应的大型空间模拟设备,进行过多次地面模拟实验。
由于地面有重力作用,当有温差存在时,地面模型的对流换热状况会与空间环境不同,造成地面实验的结果和空间微重力实际情况有一定偏差。为此,前人曾采用实验的方法来获得微重力环境,如落塔、落井、飞机、火箭等实验,但用这些方法获得的工作时间太短,无法满足实验的热稳定性要求。为了在地面模拟微重力环境下舱内的流动和换热,并保持模型的温度和材料与原型一致,必须保持Re数(Re为雷诺数,定义为Re=ρuL/μ,其中ρ为流体密度,μ为特征速度,L为特征尺度,μ为流体的动力粘性系数)相同,并尽可能地减小格拉晓夫数Gr,以抑制自然对流的影响。由Gr数的表达式Gr=ρ2gβL3T0/μ2可知,若使重力加速度g、气体膨胀系数β、参考温度T0和动力粘度μ保持不变,则减小Gr数可以通过改变密度ρ和尺寸L来实现,这样就产生了两种Gr数调整技术,即缩小尺寸的保持技术和改变压力的保持技术。这两种方法通常称为缩比法[1]和减压法。文献[2]研究了对流换热的地面相似模拟技术,提出了抑制自然对流的温度-材料-Nu数综合保持技术,即通过按比例缩小尺寸,降低Gr数,保持材料和Re数不变的办法,使自然对流的作用减弱到可以忽略的程度,从而实现模型与原型的流场和温度场的相似,实现在地面模拟微重力条件下的流动和换热。该方法的关键是使Gr/Re2小于某一临界值,使在地面时自然对流的影响可以忽略。文献[2]的作者进一步提出了地面模拟传质的技术[3]。前苏联采用过减压法进行地面模拟实验。但减压法最大的缺点是无法模拟有传质的问题[4]。这是由于饱和湿度和湿扩散系数随压力的变化很大,无法保持湿度。缩比法虽然能较好地模拟空间飞行器的流动、传热和传质,但因为空间飞行器是个非常复杂的系统,保持缩比模型和原型的完全相似很困难。所以,为了对空间飞行器的热设计提供可靠的参考,需要进行地面1∶1模型的实验,以至初样、正样实验,这是缩比法和减压法不能替代的。而如前所述,地面实验中重力的影响是无法避免的,因此,如果能把地面1∶1模型的实验结果经过某种修正,得到和微重力条件下原型比较吻合的结果,就可以通过地面直接模拟来指导空间飞行器的热设计了。本文就试图提出一种地面实验结果的修正方法。
, 百拇医药
物理数学模型
根据空间飞行器的几何结构,可将其简化为方腔来研究其中的流动和传热问题。本文研究了两种进风方式的方腔内的传热问题。第一种进风方式是45°对称间隔斜进风,如图1所示,以y轴为对称轴,两边对称,每边分成6段,其中的3段斜进风口彼此间隔开来。第二种进风方式是垂直进风,如图2所示。图1和图2中的方腔总体几何尺寸及出风方式是一样的。采用45°对称间隔斜进风方式和垂直进风方式,有利于空间飞行器舱内的通风、换热,有利于舱内空气的速度、温度、湿度均匀分布,有利于舱内空气流动稳定,以及满足舒适性的要求。从这些方面考虑,这两种进风方式,尤其是45°对称间隔斜进风方式,比均匀进风方式、小孔垂直进风方式及其它形式的斜进风方式要好一些[5]。因此,这两种方式也是空间飞行器可能采用的两种进风方式,所以本文以这两种方式为例来给出微重力修正的方法。本文对5种不同流量的工况在重力和微重力条件下这两种进风方式的原型尺寸的方腔内的流动换热情况进行了数值模拟。这5种流量对应的Re数分别为20000、30000、40000、50000、60000。

, 百拇医药
图1 空间飞行器45°间隔斜进风方式示意图
Fig.1 Interval 45°oblique air inlet pattern of spacecraft

图2 空间飞行器垂直进风方式示意图
Fig.2 Vertical air inlet pattern of spacecraft
描述方腔内空气流动和传热特性的基本方程包括连续方程、动量方程和能量方程,它们的无量纲形式分别为:
 (1)
(1)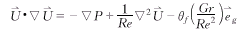 (2)
(2)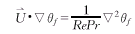 (3)
(3), 百拇医药
它们同边界条件一起,构成了舱内空气流动与传热的数学模型。在本文中,对两种进风方式都进行了等壁温边界条件下的计算,对斜进风方式,还计算了等热流边界条件下的情况。无论是等壁温还是等热流边界条件,都是对称地加在图1、图2中与x方向垂直的两个侧壁上,其余壁面均为等壁温边界条件,温度低于这两个侧面。数值模拟采用三维计算,假设方腔内流动为层流,空气物性满足Boussinesq假定。所有工况均采用65×30×85非均匀网格,SIMPLER算法[6]。
等壁温条件下壁面平均Nu数的修正
本文提出的修正公式都是换热方面的,因为流动方面的情况,通过地面的冷态实验,就可以得到和微重力条件下相同的结果。
45°间隔斜进风方式 对流换热系数是空间飞行器热设计所需要的重要参数之一,我们有必要对空间飞行器内空气在壁面的对流换热系数进行认识和研究。对空间飞行器内空气的流动和换热进行数值计算之后,可以得到其中的温度分布。根据这一温度分布,可以求得壁面热流密度qw,其表达式为:
 (4)
(4), 百拇医药
其中,λ是空气的导热系数。壁面温度梯度用3点差分格式求得。有了壁面热流密度,就可以求得对流换热系数α,可由下式求得:
 (5)
(5)其中,ΔT=Tw-Tin,是等温加热的壁面和进口之间的温差。由此得努赛尔数Nu:
 (6)
(6)在壁面上对Nu数取平均,就得到壁面平均Nu数。壁面平均Nu数反映了空气在空间飞行器内壁面上的对流换热特性。
表1列出了通过数值计算得到的不同Re数时,在重力和微重力两种情况下的壁面平均Nu数。在表1中,下标mg代表微重力情况,以重力加速度g=0.0 m/s2的情况近似[2~5],下标g代表重力情况,重力加速度g=9.8 m/s2。由表1可以看出,地面重力条件下的换热量明显大于空间微重力条件下的换热量。随着Re数的增加,壁面换热量增加。两种情况下壁面平均Nu数的比值在不同Re数时是不同的,随着Re数的增加,这一比值也增加,这表明微重力条件下换热量的增加快于重力条件下。
, 百拇医药
表1 不同Re数,重力、微重力条件下壁面Nu数
Table 1 Nu number in different Re numbers in gravity or micro-gravity condition Re/104
Numg
Nug

2.0
73.52
160.46
0.458
, 百拇医药 3.0
95.47
171.08
0.558
4.0
109.73
176.67
0.621
5.0
122.32
182.17
0.671
6.0
, 百拇医药
136.30
186.24
0.732
根据量纲分析,对受迫对流,有: Nu=f(Re,Pr) (7)
对混合对流,有:
Nu=f(Re,Gr,Pr) (8)
式中,Pr为普朗特数,Pr=μcp/λ,cp为空气的比热,本文中,对空气,Pr=0.71。参考已有的受迫对流、混合对流实验关联式[7],用已定准则幂函数形式整理本文计算所得的数据,设:
Numg=C1Rem1 (9)
, http://www.100md.com
Nug=C2Rem2Grn1 (10)
在两式中,即在微重力原型和地面模型装置中,对固定工况,Re数是保持一致的,则:
 (11)
(11)根据经验公式,取n1=1/3[7],在本文中,Gr=2.2×1010。对表1所列数据,由最小二乘法拟合,得C1=0.3182,m1=0.5510,C2=0.01521,m2=0.1342,从而得出C3=20.92,m3=0.4168,n2=-1/3。因此,可分别得到微重力原型和地面1∶1模型装置的壁面Nu数关系式:
, http://www.100md.com
Numg=0.3182Re0.5510 (12)
Nug=0.01521Re0.1342Gr1/3 (13)
由式(12)和式(13)可得及壁面平均Nu数的修正公式:
 (14)
(14)表2列出了本文数值模拟的结果和用拟合公式(12)计算所得的结果,以及这两组数据的相对误差ε。可以看出,表2中相对误差的绝对值最大不超过2.34%。用同样的方法计算了拟合公式(13)和(14)的相对误差,其绝对值均在2%以内。可以看出,由拟合公式(12),(13),(14)的计算结果与原始数据符合得很好,这说明拟合公式(12),(13),(14)可以较好地反映45°间隔斜进风时空间飞行器舱内不同工况时的换热规律。这表明我们前述对空间飞行器舱内换热规律的分析和假设是正确的。这样,只要知道1∶1地面模拟时的Re数、Gr数和Nu数,就可以根据(14)式求得
, 百拇医药
表2 数值模拟与式(12)计算所得Nu值比较
Table 2 Comparison between numerical simulation results and calculated values from equation (12) for Nu number Re/104
numerical
simulation results
fitting values
ε
2.0
73.52
74.57
, 百拇医药
1.43%
3.0
95.47
93.24
-2.34%
4.0
109.73
109.25
-0.44%
5.0
122.32
123.55
1.01%
, 百拇医药
6.0
136.30
136.60
0.22%
45°间隔斜进风时在微重力条件下的Nu数,即: Numg=20.92Re0.4168Gr-1/3Nug (15)
垂直进风方式 表3列出了数值模拟的结果。可以看出,所得结论与斜进风基本相同。地面1∶1模型装置的换热量明显大于空间飞行器原型的换热量。相同条件下,壁面换热量随流量的增加而增加,微重力条件下换热量增加快于重力条件下。与表1数据作一对比发现,在垂直进风时,微重力条件下的换热量要大于斜进风时,而在重力条件下换热量则小于斜进风时,因此,在垂直进风时,重力和微重力两种条件下壁面换热量的差别要比斜进风时小,从这个角度来看,垂直进风方式比斜进风方式更容易抑制自然对流的影响,尤其是在Gr数不变而增大Re数的情况下。
, 百拇医药
表3 不同Re数,重力、微重力条件下壁面Nu数
Table 3 Nu number in different Re numbers in gravity or micro-gravity condition Re/104
Numg
Nug

2.0
94.72
155.08
0.611
, 百拇医药 3.0
121.61
166.86
0.729
4.0
143.59
174.87
0.821
5.0
160.76
180.56
0.890
6.0
, 百拇医药
174.34
183.98
0.948
与斜进风方式的整理方法相同,对表3中的数值模拟结果按最小二乘法进行拟合,得到垂直进风等壁温条件下空间飞行器原型和地面1∶1模型装置中壁面换热公式及壁面平均Nu数的修正公式: Numg=0.3784Re0.5590 (16)
Nug=0.01169Re0.1575Gr1/3 (17)
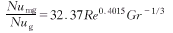 (18)
(18)式(16),(17),(18)的拟合误差的绝对值不超过2%,表明这3个拟合公式可以基本反映垂直进风时空间飞行器舱内不同工况时的换热规律。类似于公式(15),可得垂直进风时微重力条件下的Nu数的修正公式:
, 百拇医药
Numg=32.37Re0.4015Gr-1/3Nug (19)
壁面平均Nu数的通用修正公式 前面对斜进风和垂直进风两种进风方式时壁面平均Nu数提出了微重力修正公式(14)和(18),比较式(14)和式(18)可以看出,两式中Re数的指数很接近。为了便于应用,可以考虑将这两个公式合并。取两个公式中Re数指数的算术平均值作为新的合并公式中Re数的指数,并对公式的系数进行调整,可以将式(14)和式(18)合并为:
 (20)
(20)式中,斜进风时,C=22.68;直进风时,C=29.77。简单计算表明,式(20)的拟合误差的绝对值小于2%,说明此式对原始数据拟合得很好。
由此可得等壁温微重力条件下方腔壁面的Nu数的通用修正公式为:
, http://www.100md.com
Numg=CRe0.4092Gr-1/3Nug (21)
其中,常系数C随进风方式的不同而不同。
等热流条件下最高壁温的修正
在空间飞行器的热设计中,最高壁面温度也是我们所关心的一个重要参数。壁面温度如果过高,可导致仪器设备过热损坏。所以有必要对最高壁面温度进行实验预测,从而找出避免壁面温度过高的方法。
本文对某一热流密度条件下45°间隔斜进风的流动换热进行了数值模拟。表4列出了数值模拟所得到的不同工况时的壁面最高温度。可以看出,空间飞行器原型舱中的最高壁面温度要明显高于地面1∶1模型装置中的最高壁面温度。在重力和微重力两种条件下,随着流量的增加,最高壁面温度均有所下降。重力条件下,当Re数大于30000时,下降的幅度很小,最高壁面温度几乎维持不变。
, 百拇医药
表4 不同Re数,重力、微重力条件下最高壁面温度Tmax
Table 4 Maximum wall temperatures in different Re numbers in gravity or micro-gravity condition Re/104
Tmax,mg(℃)
Tmax,g(℃)
2.0
61.92
30.60
3.0
54.90
, 百拇医药
25.15
4.0
45.60
25.38
5.0
41.01
25.13
6.0
35.42
24.83
为了整理出最高壁面温度的微重力修正公式,以便于应用,对表4中的数据按指数函数形式进行最小二乘拟合,可得: Tmax,mg=9820.62Re-0.5079 (22)
, 百拇医药
Tmax,g=156.15Re-0.1698 (23)
两式的拟合误差的绝对值最大不超过7.81%,说明这两个拟合公式可以基本反映重力和微重力条件下最高壁面温度的变化情况。将式(22)和式(23)相除,得:
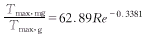 (24)
(24)由此可得等热流条件下最高壁面温度的修正公式:
Tmax,g=62.89Re-0.3381Tmax,g (25)
根据地面测得的1∶1模型的最高壁面温度及Re数,就可由式(25)求得微重力原型的最高壁面温度,从而达到对地面模型装置实验结果进行修正的目的。
, 百拇医药
结 论
本文数值计算结果表明,空间飞行器在地面的换热特性与微重力条件下有明显差别,地面的实验结果无法直接应用于微重力条件下的空间飞行器,必须经过某种修正,才能对空间飞行器的热设计提供参考依据。本文对等壁温条件下45°间隔斜进风和垂直进风的工况分别提出了修正结果和修正公式(14)、(18),并将两个修正公式合并为一个更为通用的形式;对等热流条件下45°间隔斜进风的最高壁面温度列出了修正结果和修正公式(25)。根据这些公式,可以对地面模型装置实验得到的换热特性进行修正,从而得到微重力条件下空间飞行器舱内的换热特性。
本文研究表明,随着数值计算水平的不断提高,可以提出更完善、齐备的微重力修正公式,从而更好地指导空间飞行器的热设计。实际中空间飞行器的结构是多种多样的。在实际应用中,应结合空间飞行器的具体结构和边界条件进行具体研究。本文给出的是一种方法和思路,可以对实际空间飞行器的热设计提供参考。
, 百拇医药
[参考文献]
[1] Shannon RL. Thermal scale modeling radiation-conduction-convection systems[J].Journal of Spacecraft and Rocket,1973,10(8): 485~491
[2] Liang XG, Guo ZY,Liu YL et al.Ground simulation of flow and heat transfer under micro-gravity[J].Science in China(Series A),1997,40(11): 1204~1209
[3] Liu YL,Liang XG, Ren JX et al.Ground thermal scale modeling of radiation-convective heat and mass transfer system in microgravity environment[J].Chinese Space Science and Technology,1997,27(2): 8~15
, 百拇医药
刘云龙,梁新刚,任建勋等.微重力场中对流-辐射-传质系统的地面模拟技术[J].中国空间科学技术,1997,27(2): 8~15
[4] Liu YL,Ren JX,Liang XG.Grashof number adjustment technique to suppress natural convection[J].Journal of Tsinghua University,1998,38(10): 116~118
刘云龙,任建勋,梁新刚.抑制自然对流的Gr数调整技术[J].清华大学学报,1998,38(10): 116~118
[5] 吴群刚.空间站载人舱简化结构内通风换热的数值研究[D].硕士学位论文,清华大学力学系,1999: 40~90
[6] S.V. 帕坦卡.传热与流体流动的数值计算[M].北京:科学出版社,1992: 153~157
[7] 杨世铭.传热学[M].北京:高等教育出版社,1989:184~224
收稿日期:1999-10-12, 百拇医药