血糖系统的数学模型与耐糖试验
作者：周 刘卫芳 邵颉 贾文艳
单位：周 呼和浩特铁路局中心医院(010050)；刘卫芳 邵颉 贾文艳 首都医科大学生物医学工程系(100054)
关键词：血糖系统；数学模型；耐糖试验
北京生物医学工程990414 周
刘卫芳 邵颉 贾文艳
摘 要 本文叙述了一种符合生理过程的血糖系统的非线性数学模型，其仿真的结果证明不同类型的糖尿病人的耐糖曲线是不同的，这和临床上耐糖试验的经验判据是一致的。
0 前 言
血糖系统的数学模型是生物控制论中较早的建模论题之一，这是因为血糖系统中不断进食而变化的血糖与个体差异很大的胰岛素的分泌所形成的动态平衡，是定量判断不同类型糖尿病及其正确合理用药的基础，但因人体内有极其复杂的定量关系，这类数学模型建立的种类很多，但在临床上应用仍有不足之处，以至于Bergman[1]提出生物建模的最小原则，这是早期生理建模的一段史话。实质上是建模应与生理一致(包括与临床数据相吻合)，这正是当前提倡的同胚模型的基本原则。
, 百拇医药
1 模型介绍
本文介绍的是Stolwijk[2]提出的生理模型，描述如下：
血糖的来源：(1)肝脏释放，以其释放速率Q(mg/h)表示。
(2)外界输入，以吸入速度IN(mg/h)表示。
血糖的消耗：(1)当血糖浓度x超过阈值时肾脏的排出表示为：kxSgn(x-θx)。
(2)进入细胞的消耗是一阶消耗速率，以kx0x表示。
(3)受胰岛素控制的血糖消耗正比于血糖浓度与胰岛素之乘积，表示为：kuxy
, 百拇医药 胰岛素的来源与消耗都只有一个，即胰腺释放与用于血糖消耗。故血糖的变化量为：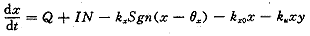
胰岛素的变化量为：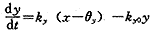
由于这个模型中有非线性项，用实测临床数据来辨识模型参数在数学上目前还做不到，因此出现了各种各样的简化模型，但都不能反映此系统的本质，对此系统的仿真却可以找到各种不同类型的糖尿病的特征，结合临床上常用的耐糖试验实测数据，可以协助临床在较简单的试验条件下对诊断和用药提供帮助。
2 仿真结果与讨论
假设耐糖试验在三类人体上作出，则给糖后的血糖变化曲线的仿真结果如图1、2、3所示。图中的平滑曲线为模型仿真结果，其余分别为临床耐糖试验中空腹、给糖后0.5h、1h、2h实测数据平均值上下一个标准差。模型中采用的各生理参数均取自本文参考文献[2]。由于图3所示的临床病例非常少，因此本文没有列出。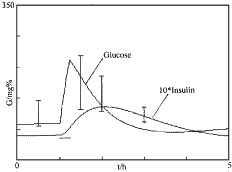
GG=13.9 BB=14.3 G=81.00 I=5.50
, http://www.100md.com
t1=1.00 t2=1.25
图1 正常情况下血糖-胰岛素代谢过程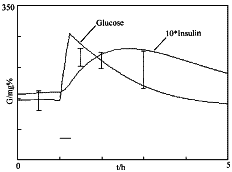
GG=2.50 BB=14.3 G=138.00 I=15.00
t1=1.00 t2=1.25
图2 胰岛素缺乏型糖尿病血糖-胰岛素代谢过程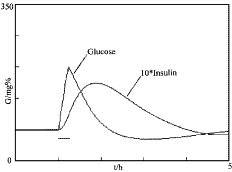
GG=13.9 BB=28.60 G=69.40 I=6.90
t1=1.00 t2=1.25
图3 有肿瘤时血糖-胰岛素代谢过程
, http://www.100md.com
可以看出：①正常人给糖后血糖数据在急剧升高，下降后趋于稳定值。
②胰岛素依赖性的血糖变化趋势是血糖上升后的下降值较高，而且趋于稳定值的过程较慢。
③对胰岛素分泌亢进型在服糖后一段时间后血糖值是处于较低的水平上。
因此，耐糖试验规定进服葡萄糖后要测三个血糖值(再多的数据一则花费较大，以及患者不愿配合)。第一个数相当于血糖曲线的高峰值，反映患者的生理状况、个体差异等因素；第二个数反映了是否是胰岛素依赖性的糖尿病的特征；第三个数反映了血糖恢复正常的情况。耐糖试验的三个数据的统计数值对于判断糖尿病类型及合理给药有一定帮助。
为临床应用方便，也有采用三次进食后的一小时血糖值作为耐糖试验的数值，这相当于多次重复给药的情况，只是给糖量较低的情况仿真结果也可以看出，其特征将另文讨论。
, http://www.100md.com
基金项目：本文受北京市教委教改项目支持。
作者简介：周，男，42岁，呼和浩特铁路局中心医院 主治医师
作者单位：周 呼和浩特铁路局中心医院(010050)
刘卫芳 邵颉 贾文艳 首都医科大学生物医学工程系(100054)
参考文献
1 Bergman R N, et al. Interaction of insulin and glucose in the control of hepatic glucose balance. Am J Physiol,1974,227:1314
2 Stolwijk J A, et al. Regulation and control in physiology. Chapter 57 in Medical physiology. Mountcastle V B Ed st. Louis:Mosby C V CO. 1974, 百拇医药
单位：周 呼和浩特铁路局中心医院(010050)；刘卫芳 邵颉 贾文艳 首都医科大学生物医学工程系(100054)
关键词：血糖系统；数学模型；耐糖试验
北京生物医学工程990414 周
刘卫芳 邵颉 贾文艳摘 要 本文叙述了一种符合生理过程的血糖系统的非线性数学模型，其仿真的结果证明不同类型的糖尿病人的耐糖曲线是不同的，这和临床上耐糖试验的经验判据是一致的。
0 前 言
血糖系统的数学模型是生物控制论中较早的建模论题之一，这是因为血糖系统中不断进食而变化的血糖与个体差异很大的胰岛素的分泌所形成的动态平衡，是定量判断不同类型糖尿病及其正确合理用药的基础，但因人体内有极其复杂的定量关系，这类数学模型建立的种类很多，但在临床上应用仍有不足之处，以至于Bergman[1]提出生物建模的最小原则，这是早期生理建模的一段史话。实质上是建模应与生理一致(包括与临床数据相吻合)，这正是当前提倡的同胚模型的基本原则。
, 百拇医药
1 模型介绍
本文介绍的是Stolwijk[2]提出的生理模型，描述如下：
血糖的来源：(1)肝脏释放，以其释放速率Q(mg/h)表示。
(2)外界输入，以吸入速度IN(mg/h)表示。
血糖的消耗：(1)当血糖浓度x超过阈值时肾脏的排出表示为：kxSgn(x-θx)。
(2)进入细胞的消耗是一阶消耗速率，以kx0x表示。
(3)受胰岛素控制的血糖消耗正比于血糖浓度与胰岛素之乘积，表示为：kuxy
, 百拇医药 胰岛素的来源与消耗都只有一个，即胰腺释放与用于血糖消耗。故血糖的变化量为：
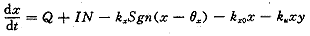
胰岛素的变化量为：
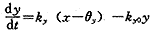
由于这个模型中有非线性项，用实测临床数据来辨识模型参数在数学上目前还做不到，因此出现了各种各样的简化模型，但都不能反映此系统的本质，对此系统的仿真却可以找到各种不同类型的糖尿病的特征，结合临床上常用的耐糖试验实测数据，可以协助临床在较简单的试验条件下对诊断和用药提供帮助。
2 仿真结果与讨论
假设耐糖试验在三类人体上作出，则给糖后的血糖变化曲线的仿真结果如图1、2、3所示。图中的平滑曲线为模型仿真结果，其余分别为临床耐糖试验中空腹、给糖后0.5h、1h、2h实测数据平均值上下一个标准差。模型中采用的各生理参数均取自本文参考文献[2]。由于图3所示的临床病例非常少，因此本文没有列出。
GG=13.9 BB=14.3 G=81.00 I=5.50, http://www.100md.com
t1=1.00 t2=1.25
图1 正常情况下血糖-胰岛素代谢过程
GG=2.50 BB=14.3 G=138.00 I=15.00t1=1.00 t2=1.25
图2 胰岛素缺乏型糖尿病血糖-胰岛素代谢过程
GG=13.9 BB=28.60 G=69.40 I=6.90t1=1.00 t2=1.25
图3 有肿瘤时血糖-胰岛素代谢过程
, http://www.100md.com
可以看出：①正常人给糖后血糖数据在急剧升高，下降后趋于稳定值。
②胰岛素依赖性的血糖变化趋势是血糖上升后的下降值较高，而且趋于稳定值的过程较慢。
③对胰岛素分泌亢进型在服糖后一段时间后血糖值是处于较低的水平上。
因此，耐糖试验规定进服葡萄糖后要测三个血糖值(再多的数据一则花费较大，以及患者不愿配合)。第一个数相当于血糖曲线的高峰值，反映患者的生理状况、个体差异等因素；第二个数反映了是否是胰岛素依赖性的糖尿病的特征；第三个数反映了血糖恢复正常的情况。耐糖试验的三个数据的统计数值对于判断糖尿病类型及合理给药有一定帮助。
为临床应用方便，也有采用三次进食后的一小时血糖值作为耐糖试验的数值，这相当于多次重复给药的情况，只是给糖量较低的情况仿真结果也可以看出，其特征将另文讨论。
, http://www.100md.com
基金项目：本文受北京市教委教改项目支持。
作者简介：周
，男，42岁，呼和浩特铁路局中心医院 主治医师作者单位：周
呼和浩特铁路局中心医院(010050)刘卫芳 邵颉 贾文艳 首都医科大学生物医学工程系(100054)
参考文献
1 Bergman R N, et al. Interaction of insulin and glucose in the control of hepatic glucose balance. Am J Physiol,1974,227:1314
2 Stolwijk J A, et al. Regulation and control in physiology. Chapter 57 in Medical physiology. Mountcastle V B Ed st. Louis:Mosby C V CO. 1974, 百拇医药