相应分析及其在多种疾病聚集性分析中的应用*
作者:陈峰 杨树勤
单位:陈峰 南通医学院(226001); 杨树勤 华西医科大学
关键词:
中国卫生统计990219 相应分析(correspondence analysis),又称对应分析,由法国数学家JP.Beozecri在1970年首次提出〔1〕,主要用于分析二维数据阵中行因素和列因素间的关系。传统的因子分析只能对数据阵单独进行R-型(列因素)或Q-型(行因素)因子分析(factor analysis),不能同时对行因素和列因素进行分析。这就将行因素与列因素隔裂开来了,从而遗漏了许多有用的信息。事实上,有时行因素与列因素是不可分割的。比如在研究不同地区,不同种类的出生缺陷发生率时,我们既关心不同种类出生缺陷间的关系,不同地区间的关系,又想了解出生缺陷与地区间的关系。此时需要对出生缺陷(列因素)和地区(行因素)同时进行因子分析,相应分析揭示了内在联系〔2〕。
, http://www.100md.com
在JP.Beozecri提出相应分析之初,该法并未引起学界的关注,直到1974年MO.Hill在Applied Statistics杂志上以《相应分析——一种被忽视的多元分析方法》为题,再度介绍了该法及其优点之后才引起人们的兴趣。相应分析在医学上的应用也是成功的,如
Hill(1982)对5 387名中学生眼睛和头发的颜色的分析〔3〕;Greenacre(1984)对Israeli成年人关注的社会问题的分析〔4〕;Greenacre(1984)对止痛药的分类问题的分析〔5〕;Micciolo等(1985)用于复发性酒精胰腺炎手术的危险因素的分析〔6〕;Leclerc等(1988)用于医务人员的职业特点与健康状况关系的分析〔7〕等等,均取得较好的效果。
本文旨在介绍这一方法的基本思想,以及对结果的解释。
, http://www.100md.com
基本思想
相应分析的基本思想是对数据阵进行适当的变换,使变换后的数据对行与对列是相对应的,从而可以同时对行和对列进行分析,以发现行列因素间的关系。设有n×m的数据阵X={xij},行列分别表示两个不同因素的n个水平和m个水平。首先定义分布轮廓的概念。
各行在列变量上的分布(构成比)称为该行的分布轮廓(profile)或形象,即第i行的分布轮廓为:
其和为1(或100%)。其中,xi.为第i行的合计。
对应地,第j列的分布轮廓为: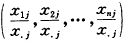
, http://www.100md.com
其和亦为1(或100%)。其中,x.j为第j列的合计。
相应分析之目的是从数据阵中概括出行列因素的最基本的分布特征,使之反映数据阵的主要信息,寻找行、列因素间的关系。
为同时对行和对列进行分析,首先对数据阵进行如下变换:
(1)
再对变换后的数据阵Z进行R-型和Q-型因子分析。进行R-型因子分析是从矩阵Am×m=Z′Z出发,求其特征根和特征向量;进行Q-型因子分析是从矩阵Bn×n=ZZ′出发,求其特征根和特征向量。
由于矩阵Z′Z和ZZ′具有相同的非零特征根,且对同一特征根λ,如Φ是Z′Z的特征向量,则Ψ=ZΦ是ZZ′的特征向量。A与B的这种对应关系,使得变换后的数据对行与对列是对等的,从而可以将行因素和列因素相提并论。
, http://www.100md.com
将A的第1因子和第2因子绘在因子负荷图上可以进行R-型因子分析;将B的第1因子和第2因子绘在因子负荷图上可以进行Q-型因子分析。又由于A和B的特征根相同,故相应的因子贡献率亦相同,因而可以将两者对应起来进行分析,即将A的第1因子和第2因子及B的第1因子和第2因子同时绘在同一坐标轴上,则可揭示行因素的不同水平及列因素的不同水平间的关系。
可见,变换是相应分析的关键所在。而其余的分析与因子分析类似,只是在因子的解释上,既可以对行因素及列因素单独进行分析,又可以同时进行分析。这是相应分析的优点。
基本步骤
下面先从一个构想的例子来说明相应分析的计算步骤及结果的解释。
构想的例子:这个例子包含了5行4列,数据见表1。
表1 构想的数据
, 百拇医药
y1
y2
y3
y4
合计
x1
50
20
20
10
100
x2
, http://www.100md.com
100
40
40
20
200
x3
30
60
60
150
300
x4
100
, http://www.100md.com
100
100
100
400
x5
140
110
110
140
500
合计
420
330
, 百拇医药
330
420
1500
其行轮廓和列轮廓分别为:
行轮廓(%):
x1:50.0 20.0 20.0 10.0
x2:50.0 20.0 20.0 10.0
x3:10.0 20.0 20.0 50.0
x4:25.0 25.0 25.0 25.0
x5:28.0 22.0 22.0 28.0
, 百拇医药
列轮廓(%): y1
y2
y3
y4
11.9
6.1
6.1
2.4
23.8
12.1
12.1
4.8
, 百拇医药
7.1
18.2
18.2
35.7
23.8
30.3
30.3
23.8
33.3
33.3
33.3
33.3
从行轮廓来看,x1与x2的构成相同,且在y1上的取值最大;x3则在y4上的取值最大;x4在y1,y2,y3,y4上的构成是均匀的,但相对其他行变量x4在y2,y3上的取值比在y1,y4要大一些;x5的构成等于合计的构成,即等于总平均。
, http://www.100md.com
从列轮廓来看,y2与y3构成相同,其余则不同;y1,y2,y3在x5上的取值最大,而y4则是在x3上最大。
计算步骤:
(1)按式(1)作变换,求Z={zij};
(2)计算Z′Z得:
(3)求Z′Z的特征根及单位化特征向量:
Z′Z的非0特征根个数最多为“行数”和“列数”中最小者。且必有一个特征根为1,但其对应的特征向量为(1,1,1,1)′,该向量对各变量的表达是平等的,这对因子的解释毫无帮助,称之为平凡因子,故不加考虑。因此,Z′Z的非平凡特征根的个数最多为:
, http://www.100md.com
min(行数-1,列数-1)
(2)
本例两个非平凡特征根为:
λ1=0.1143 λ2=0.0065
贡献率分别为94.62%和5.38%。对应于这两个特征根的单位化特征向量Φi1,Φi2为:
(4)按式(3)求因子负荷,结果见表2第2,3栏。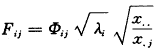
(3)
, 百拇医药
(5)求ZZ′的特征根并将其单位化,得: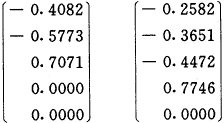
(6)按式(4)求ZZ′的因子负荷,结果见表2第5,6栏。
(4)
表2 构想例子的因子负荷(坐标) 行因素
因子负荷
列因素
因子负荷
F1
F2
, 百拇医药
F1
F2
y1
-0.4517
-0.0714
x1
-0.5345
-0.0806
y2
0.0000
0.0909
, http://www.100md.com x2
-0.5345
-0.0806
y3
0.0000
0.0909
x3
0.5345
-0.0806
y4
0.4517
-0.0714
, 百拇医药
x4
0.0000
0.1209
x5
0.0000
0.0000
将行列因素的F1,F2同时绘在OF1F2平面坐标上,得图1。行列因素间的关系在因子负荷图上一目了然。
图1 模拟例子的相应分析因子负荷图
(1)轮廓相近的两水平在因子负荷图上的点相近,当两个轮廓完全相同时,两点合为一点。如,x1,x2的行轮廓相同,故两点合为一点;y2,y3的列轮廓相同,故两点合为一点。
, 百拇医药
(2)行(列)轮廓在列(行)因素某水平上取值最大,则相应的两点在因子负荷图上是相近的。如,x3在y4上取值最大,故x3最接近y4;x4在y2,y3上取值比其他行变量大,故x4最接近y2、y3;x1,x2的构成在y1上取值最大,故x1,x2最接近y1。
(3)轮廓相反(构成比相反)的两点在因子负荷图上相隔较远,其所在的位置将视具体情况而定。如,x1与x3在y1,y4上的取值正好相反,因此两者相隔较远,而同时x1与x3在y2,y3上取值相同,因此,x1与x3正好关于Oy2,Oy3构成一镜面映射。
, 百拇医药
(4)坐标轴的原点对应于行轮廓或列轮廓的平均水平。如,x5的轮廓等于平均水平,故x5在坐标原点。
由此可见,轮廓相同的行(或列)在相应分析中提供了相同的信息,当合并这些行(或列)时不改变分析的结果。事实上,将两个性质相同的事物合并在一起,看成一个事物不会损失信息;而将同一事物分成两个一样的事物亦不会获得更多的信息。
综上分析,x1,x2与y1密切,x4又与y2,y3密切,而x3与y4密切,并将其视为三类,x5为一平均水平,成为单独一类。
实例分析——多种疾病的地区聚集性分析
, http://www.100md.com 王绍贤等对我国九个城市1986年的城区及农村(或郊区)11 764名20~40岁的已婚妇女进行了婚姻、生育、避孕情况的调查。该调查表明,调查地区城区避孕率为87.7%,农村略低于城区,为81.0%。避孕方法一般采用宫内器,口服药,男用套,绝育,和其他一些短效方法。本文选择其中九市(省)城乡的避孕资料进行相应分析,旨在进一步探讨不同地区的避孕状况,以及城乡之间的差别。
表3 九个城市1986年的城区及农村几种避孕方法调查人数
宫内器
口服药
男用套
绝 育
其 他
合 计
, http://www.100md.com
城
区
北京
153
33
165
40
40
431
吉林
346
10
15
76
, 百拇医药
10
457
成都
241
38
134
21
35
469
长沙
184
21
106
, 百拇医药 64
60
435
大连
367
18
129
11
25
550
西安
703
55
130
, 百拇医药
69
83
1040
郑州
248
12
113
60
30
463
重庆
296
20
, 百拇医药 87
36
26
465
武汉
476
79
113
82
91
841
农
村
或
, 百拇医药
郊
区
北京
320
75
43
62
18
518
吉林
249
6
10
119
, 百拇医药
8
392
成都
278
38
22
141
36
515
长沙
73
4
13
323
, 百拇医药
10
423
大连
209
43
66
100
7
425
西安
288
4
0
418
, 百拇医药
1
711
郑州
141
6
1
294
1
443
重庆
435
1
2
73
, 百拇医药
2
513
武汉
364
164
4
277
16
825
这是一18×5的列联表。按(1)作变换,计算矩阵A及B,求得4个非平凡因子,4个特征根分别为:0.27222,0.08900,0.04444,0.01301,其贡献率分别为:65.02%,21.26%,10.62%,3.11%。前两个因子的累计贡献率大于80%。据公式(2)及(3)可得行因素及列因素的第1和第2因子,分列于表4和表5。表4 地区(行因素)的因子负荷 地区
, http://www.100md.com
城 区
农 村
第1因子F1
第2因子F2
第1因子F1
第2因子F2
北京
0.56306
0.62225
0.18139
-0.21509
, 百拇医药 吉林
0.01268
-0.43995
-0.27299
-0.27268
成都
0.55377
0.25245
-0.15808
-0.10446
长沙
0.33987
, 百拇医药 0.38274
-1.20018
0.40569
大连
0.52797
-0.03476
0.00032
0.06429
西安
0.34908
-0.17661
-0.88907
, 百拇医药
0.01622
郑州
0.32412
0.18067
-1.03954
0.14231
重庆
0.37297
-0.04954
0.01952
-0.61180
武汉
, http://www.100md.com 0.31860
-0.00546
-0.34070
-0.09697
表5 避孕方法(列因素)的因子负荷 避孕方法
第1因子F1
第2因子F2
宫内器
0.157865
-0.249945
口服药
, http://www.100md.com 0.215731
0.056393
男用套
0.676448
0.569611
绝 育
-0.902338
0.179357
其 他
0.493449
0.376949
将行因素及列因素的第1、第2因子负荷绘在同一因子图上,得图2。
, http://www.100md.com
图2 不同地区避孕方式的相应分析因子负荷图
由图2可见,“绝育”远离城区数据群,说明城区居民不喜欢该法;“口服药”、“男用套”远离农村数据群,说明农村居民不喜欢这些方法;而长沙、郑州、西安三市农村“绝育”者较其余地区为多,其他地区则以“宫内器”和“其他”短效方法为主要避孕方法;此外又进一步清晰地显示了城区和农村的两种不同的避孕模式。因子负荷形成了两大数据群:大的圆圈中包括所有的农村地区,其间包括了“绝育”、“口服药”和“宫内器”三种避孕方法;小的圆圈中包括所有的城市地区,其间包括了“口服药”、“宫内器”、“男用套”和“其他短效避孕方法”。这两个数据群亦有部分交叉。由此可认为“口服药”、“宫内器”两种避孕方法在大部分地区较受欢迎;而在城市用“绝育”法避孕者较少;农村中,长沙、郑州、西安“绝育”者较多,农村普遍不喜欢“男用套”和“其他短效避孕方法”。
应用中的几个问题
相应分析是因子分析的自然推广,在对因子的解释上,既可以对行因素及列因素单独进行解释,又可以同时进行分析。
, http://www.100md.com
相应分析和因子分析一样,均未要求对特征根进行假设检验。由于相应分析大都基于前两个因子进行的,这就要求前两个因子的累计贡献率要大一些,一般要求达到80%。
相应分析最早用于处理列联表资料,即数据是正整数,现也用于处理非整数资料〔2〕。一般要求数据不小于0。若有数据小于0,则所有数据加上一适当的常数即可。
相应分析的关键是对数据阵进行变换,本文所用方法(1)是基于原点的变换。相应分析亦可基于重心来分析,即用(5)式代替(1)式。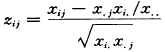
(5)
i=1,2,…,n;j=1,2,…,m
用第一因子按因子负荷对行因素和列因素进行排序,并依次对行和列重排,则可得到列联表的最优列联表示。
, http://www.100md.com
相应分析可用软件SPSS4.0以上版本或SAS6.04以上版本进行分析。
*本课题为国家自然科学基金资助项目
参考文献
1.胡国定,张润楚.多元数据分析方法——纯代数处理.天津:南开大学出版社,1989,231~258
2.陈峰,杨树勤,吴艳乔.出生缺陷地区聚集性的相应分析.现代预防医学,1995,22(3):161~163
3.Hill MO.Correspondence analysis.In:Encyclopedia of statistics science.New York(Kotz & Johnson ed)Wiley.1982,2:204~210
4.Greenacre M.Theory and applications of correspondence analysis.London Academic Press INC.1984.
, http://www.100md.com
5.Micciolo R.Correspondence analysis in a study of the clinical evolution of uncomplicated chronic relapsing alcoholic pancreatitis.Statistics in Medicine.1985;4:303~309
6.LeclercA.Correspondence analysis and logistic modeling:complementary using the analysis of a health survey among nurses.Statistics in Medicine.1988;7:983~995
7.王绍贤.中国九市城乡决定生育力的直接因素研究.中国卫生统计.1989,6(专辑1):50~55, 百拇医药
单位:陈峰 南通医学院(226001); 杨树勤 华西医科大学
关键词:
中国卫生统计990219 相应分析(correspondence analysis),又称对应分析,由法国数学家JP.Beozecri在1970年首次提出〔1〕,主要用于分析二维数据阵中行因素和列因素间的关系。传统的因子分析只能对数据阵单独进行R-型(列因素)或Q-型(行因素)因子分析(factor analysis),不能同时对行因素和列因素进行分析。这就将行因素与列因素隔裂开来了,从而遗漏了许多有用的信息。事实上,有时行因素与列因素是不可分割的。比如在研究不同地区,不同种类的出生缺陷发生率时,我们既关心不同种类出生缺陷间的关系,不同地区间的关系,又想了解出生缺陷与地区间的关系。此时需要对出生缺陷(列因素)和地区(行因素)同时进行因子分析,相应分析揭示了内在联系〔2〕。
, http://www.100md.com
在JP.Beozecri提出相应分析之初,该法并未引起学界的关注,直到1974年MO.Hill在Applied Statistics杂志上以《相应分析——一种被忽视的多元分析方法》为题,再度介绍了该法及其优点之后才引起人们的兴趣。相应分析在医学上的应用也是成功的,如
Hill(1982)对5 387名中学生眼睛和头发的颜色的分析〔3〕;Greenacre(1984)对Israeli成年人关注的社会问题的分析〔4〕;Greenacre(1984)对止痛药的分类问题的分析〔5〕;Micciolo等(1985)用于复发性酒精胰腺炎手术的危险因素的分析〔6〕;Leclerc等(1988)用于医务人员的职业特点与健康状况关系的分析〔7〕等等,均取得较好的效果。
本文旨在介绍这一方法的基本思想,以及对结果的解释。
, http://www.100md.com
基本思想
相应分析的基本思想是对数据阵进行适当的变换,使变换后的数据对行与对列是相对应的,从而可以同时对行和对列进行分析,以发现行列因素间的关系。设有n×m的数据阵X={xij},行列分别表示两个不同因素的n个水平和m个水平。首先定义分布轮廓的概念。
各行在列变量上的分布(构成比)称为该行的分布轮廓(profile)或形象,即第i行的分布轮廓为:

其和为1(或100%)。其中,xi.为第i行的合计。
对应地,第j列的分布轮廓为:
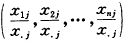
, http://www.100md.com
其和亦为1(或100%)。其中,x.j为第j列的合计。
相应分析之目的是从数据阵中概括出行列因素的最基本的分布特征,使之反映数据阵的主要信息,寻找行、列因素间的关系。
为同时对行和对列进行分析,首先对数据阵进行如下变换:

(1)
再对变换后的数据阵Z进行R-型和Q-型因子分析。进行R-型因子分析是从矩阵Am×m=Z′Z出发,求其特征根和特征向量;进行Q-型因子分析是从矩阵Bn×n=ZZ′出发,求其特征根和特征向量。
由于矩阵Z′Z和ZZ′具有相同的非零特征根,且对同一特征根λ,如Φ是Z′Z的特征向量,则Ψ=ZΦ是ZZ′的特征向量。A与B的这种对应关系,使得变换后的数据对行与对列是对等的,从而可以将行因素和列因素相提并论。
, http://www.100md.com
将A的第1因子和第2因子绘在因子负荷图上可以进行R-型因子分析;将B的第1因子和第2因子绘在因子负荷图上可以进行Q-型因子分析。又由于A和B的特征根相同,故相应的因子贡献率亦相同,因而可以将两者对应起来进行分析,即将A的第1因子和第2因子及B的第1因子和第2因子同时绘在同一坐标轴上,则可揭示行因素的不同水平及列因素的不同水平间的关系。
可见,变换是相应分析的关键所在。而其余的分析与因子分析类似,只是在因子的解释上,既可以对行因素及列因素单独进行分析,又可以同时进行分析。这是相应分析的优点。
基本步骤
下面先从一个构想的例子来说明相应分析的计算步骤及结果的解释。
构想的例子:这个例子包含了5行4列,数据见表1。
表1 构想的数据
, 百拇医药
y1
y2
y3
y4
合计
x1
50
20
20
10
100
x2
, http://www.100md.com
100
40
40
20
200
x3
30
60
60
150
300
x4
100
, http://www.100md.com
100
100
100
400
x5
140
110
110
140
500
合计
420
330
, 百拇医药
330
420
1500
其行轮廓和列轮廓分别为:
行轮廓(%):
x1:50.0 20.0 20.0 10.0
x2:50.0 20.0 20.0 10.0
x3:10.0 20.0 20.0 50.0
x4:25.0 25.0 25.0 25.0
x5:28.0 22.0 22.0 28.0
, 百拇医药
列轮廓(%): y1
y2
y3
y4
11.9
6.1
6.1
2.4
23.8
12.1
12.1
4.8
, 百拇医药
7.1
18.2
18.2
35.7
23.8
30.3
30.3
23.8
33.3
33.3
33.3
33.3
从行轮廓来看,x1与x2的构成相同,且在y1上的取值最大;x3则在y4上的取值最大;x4在y1,y2,y3,y4上的构成是均匀的,但相对其他行变量x4在y2,y3上的取值比在y1,y4要大一些;x5的构成等于合计的构成,即等于总平均。
, http://www.100md.com
从列轮廓来看,y2与y3构成相同,其余则不同;y1,y2,y3在x5上的取值最大,而y4则是在x3上最大。
计算步骤:
(1)按式(1)作变换,求Z={zij};
(2)计算Z′Z得:

(3)求Z′Z的特征根及单位化特征向量:
Z′Z的非0特征根个数最多为“行数”和“列数”中最小者。且必有一个特征根为1,但其对应的特征向量为(1,1,1,1)′,该向量对各变量的表达是平等的,这对因子的解释毫无帮助,称之为平凡因子,故不加考虑。因此,Z′Z的非平凡特征根的个数最多为:
, http://www.100md.com
min(行数-1,列数-1)
(2)
本例两个非平凡特征根为:
λ1=0.1143 λ2=0.0065
贡献率分别为94.62%和5.38%。对应于这两个特征根的单位化特征向量Φi1,Φi2为:

(4)按式(3)求因子负荷,结果见表2第2,3栏。
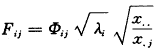
(3)
, 百拇医药
(5)求ZZ′的特征根并将其单位化,得:

(6)按式(4)求ZZ′的因子负荷,结果见表2第5,6栏。

(4)
表2 构想例子的因子负荷(坐标) 行因素
因子负荷
列因素
因子负荷
F1
F2
, 百拇医药
F1
F2
y1
-0.4517
-0.0714
x1
-0.5345
-0.0806
y2
0.0000
0.0909
, http://www.100md.com x2
-0.5345
-0.0806
y3
0.0000
0.0909
x3
0.5345
-0.0806
y4
0.4517
-0.0714
, 百拇医药
x4
0.0000
0.1209
x5
0.0000
0.0000
将行列因素的F1,F2同时绘在OF1F2平面坐标上,得图1。行列因素间的关系在因子负荷图上一目了然。

图1 模拟例子的相应分析因子负荷图
(1)轮廓相近的两水平在因子负荷图上的点相近,当两个轮廓完全相同时,两点合为一点。如,x1,x2的行轮廓相同,故两点合为一点;y2,y3的列轮廓相同,故两点合为一点。
, 百拇医药
(2)行(列)轮廓在列(行)因素某水平上取值最大,则相应的两点在因子负荷图上是相近的。如,x3在y4上取值最大,故x3最接近y4;x4在y2,y3上取值比其他行变量大,故x4最接近y2、y3;x1,x2的构成在y1上取值最大,故x1,x2最接近y1。
(3)轮廓相反(构成比相反)的两点在因子负荷图上相隔较远,其所在的位置将视具体情况而定。如,x1与x3在y1,y4上的取值正好相反,因此两者相隔较远,而同时x1与x3在y2,y3上取值相同,因此,x1与x3正好关于Oy2,Oy3构成一镜面映射。
, 百拇医药
(4)坐标轴的原点对应于行轮廓或列轮廓的平均水平。如,x5的轮廓等于平均水平,故x5在坐标原点。
由此可见,轮廓相同的行(或列)在相应分析中提供了相同的信息,当合并这些行(或列)时不改变分析的结果。事实上,将两个性质相同的事物合并在一起,看成一个事物不会损失信息;而将同一事物分成两个一样的事物亦不会获得更多的信息。
综上分析,x1,x2与y1密切,x4又与y2,y3密切,而x3与y4密切,并将其视为三类,x5为一平均水平,成为单独一类。
实例分析——多种疾病的地区聚集性分析
, http://www.100md.com 王绍贤等对我国九个城市1986年的城区及农村(或郊区)11 764名20~40岁的已婚妇女进行了婚姻、生育、避孕情况的调查。该调查表明,调查地区城区避孕率为87.7%,农村略低于城区,为81.0%。避孕方法一般采用宫内器,口服药,男用套,绝育,和其他一些短效方法。本文选择其中九市(省)城乡的避孕资料进行相应分析,旨在进一步探讨不同地区的避孕状况,以及城乡之间的差别。
表3 九个城市1986年的城区及农村几种避孕方法调查人数
宫内器
口服药
男用套
绝 育
其 他
合 计
, http://www.100md.com
城
区
北京
153
33
165
40
40
431
吉林
346
10
15
76
, 百拇医药
10
457
成都
241
38
134
21
35
469
长沙
184
21
106
, 百拇医药 64
60
435
大连
367
18
129
11
25
550
西安
703
55
130
, 百拇医药
69
83
1040
郑州
248
12
113
60
30
463
重庆
296
20
, 百拇医药 87
36
26
465
武汉
476
79
113
82
91
841
农
村
或
, 百拇医药
郊
区
北京
320
75
43
62
18
518
吉林
249
6
10
119
, 百拇医药
8
392
成都
278
38
22
141
36
515
长沙
73
4
13
323
, 百拇医药
10
423
大连
209
43
66
100
7
425
西安
288
4
0
418
, 百拇医药
1
711
郑州
141
6
1
294
1
443
重庆
435
1
2
73
, 百拇医药
2
513
武汉
364
164
4
277
16
825
这是一18×5的列联表。按(1)作变换,计算矩阵A及B,求得4个非平凡因子,4个特征根分别为:0.27222,0.08900,0.04444,0.01301,其贡献率分别为:65.02%,21.26%,10.62%,3.11%。前两个因子的累计贡献率大于80%。据公式(2)及(3)可得行因素及列因素的第1和第2因子,分列于表4和表5。表4 地区(行因素)的因子负荷 地区
, http://www.100md.com
城 区
农 村
第1因子F1
第2因子F2
第1因子F1
第2因子F2
北京
0.56306
0.62225
0.18139
-0.21509
, 百拇医药 吉林
0.01268
-0.43995
-0.27299
-0.27268
成都
0.55377
0.25245
-0.15808
-0.10446
长沙
0.33987
, 百拇医药 0.38274
-1.20018
0.40569
大连
0.52797
-0.03476
0.00032
0.06429
西安
0.34908
-0.17661
-0.88907
, 百拇医药
0.01622
郑州
0.32412
0.18067
-1.03954
0.14231
重庆
0.37297
-0.04954
0.01952
-0.61180
武汉
, http://www.100md.com 0.31860
-0.00546
-0.34070
-0.09697
表5 避孕方法(列因素)的因子负荷 避孕方法
第1因子F1
第2因子F2
宫内器
0.157865
-0.249945
口服药
, http://www.100md.com 0.215731
0.056393
男用套
0.676448
0.569611
绝 育
-0.902338
0.179357
其 他
0.493449
0.376949
将行因素及列因素的第1、第2因子负荷绘在同一因子图上,得图2。

, http://www.100md.com
图2 不同地区避孕方式的相应分析因子负荷图
由图2可见,“绝育”远离城区数据群,说明城区居民不喜欢该法;“口服药”、“男用套”远离农村数据群,说明农村居民不喜欢这些方法;而长沙、郑州、西安三市农村“绝育”者较其余地区为多,其他地区则以“宫内器”和“其他”短效方法为主要避孕方法;此外又进一步清晰地显示了城区和农村的两种不同的避孕模式。因子负荷形成了两大数据群:大的圆圈中包括所有的农村地区,其间包括了“绝育”、“口服药”和“宫内器”三种避孕方法;小的圆圈中包括所有的城市地区,其间包括了“口服药”、“宫内器”、“男用套”和“其他短效避孕方法”。这两个数据群亦有部分交叉。由此可认为“口服药”、“宫内器”两种避孕方法在大部分地区较受欢迎;而在城市用“绝育”法避孕者较少;农村中,长沙、郑州、西安“绝育”者较多,农村普遍不喜欢“男用套”和“其他短效避孕方法”。
应用中的几个问题
相应分析是因子分析的自然推广,在对因子的解释上,既可以对行因素及列因素单独进行解释,又可以同时进行分析。
, http://www.100md.com
相应分析和因子分析一样,均未要求对特征根进行假设检验。由于相应分析大都基于前两个因子进行的,这就要求前两个因子的累计贡献率要大一些,一般要求达到80%。
相应分析最早用于处理列联表资料,即数据是正整数,现也用于处理非整数资料〔2〕。一般要求数据不小于0。若有数据小于0,则所有数据加上一适当的常数即可。
相应分析的关键是对数据阵进行变换,本文所用方法(1)是基于原点的变换。相应分析亦可基于重心来分析,即用(5)式代替(1)式。
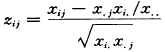
(5)
i=1,2,…,n;j=1,2,…,m
用第一因子按因子负荷对行因素和列因素进行排序,并依次对行和列重排,则可得到列联表的最优列联表示。
, http://www.100md.com
相应分析可用软件SPSS4.0以上版本或SAS6.04以上版本进行分析。
*本课题为国家自然科学基金资助项目
参考文献
1.胡国定,张润楚.多元数据分析方法——纯代数处理.天津:南开大学出版社,1989,231~258
2.陈峰,杨树勤,吴艳乔.出生缺陷地区聚集性的相应分析.现代预防医学,1995,22(3):161~163
3.Hill MO.Correspondence analysis.In:Encyclopedia of statistics science.New York(Kotz & Johnson ed)Wiley.1982,2:204~210
4.Greenacre M.Theory and applications of correspondence analysis.London Academic Press INC.1984.
, http://www.100md.com
5.Micciolo R.Correspondence analysis in a study of the clinical evolution of uncomplicated chronic relapsing alcoholic pancreatitis.Statistics in Medicine.1985;4:303~309
6.LeclercA.Correspondence analysis and logistic modeling:complementary using the analysis of a health survey among nurses.Statistics in Medicine.1988;7:983~995
7.王绍贤.中国九市城乡决定生育力的直接因素研究.中国卫生统计.1989,6(专辑1):50~55, 百拇医药