多服务台负指数分布排队系统在设备管理中的应用
作者:郭才宁 李胜利
单位:410013 长沙,湖南医科大学附属第三医院
关键词:
中华医院管理杂志991032
中华医院管理杂志
CHINESE JOURNAL OF
HOSPITAL ADMINISTRATION
1999年 第15卷 第10期 Vol.15 No.10 1999
, 百拇医药
多服务台负指数分布排队系统在设备管理中的应用
郭才宁 李胜利
排队论,也称随机服务系统理论。排队是在日常生活中经常遇到的现象,在医院中,目前要求服务的数量通常都超过服务机构的容量。对服务系统进行定量分析,综合平衡患者与服务机构的设置,以期提高服务质量。
一、资料来源与方法
(一)根据我院超声科的调查,应用排队论的理论和方法评价与优化该服务系统。超声科有3台B超仪,机构形式是单队——多服务台的情形,服务时间是随机的,服务时间的分布假定平稳,即分布的参数不受时间的影响。调查内容是单位时间内到达的患者数与服务时间。
(二)单位时间内到达的患者数:每10分钟为一个调查单位,随机调查72个调查单位,记录每个调查单位内到达的患者数,结果见表1:
, 百拇医药
表1 单位调查时间的患者人数及频度
患者数(i)
出现的频数(fi)
0
24
1
33
2
10
3
4
4
1
, 百拇医药
5
0
合计
72
(三)服务时间:从为患者开始做B超检查(包括准备工作)时记起,到患者做完检查离去为止,随机调查113个患者的服务时间。不同服务时间的出现频(次)数见表2:表2 为每位患者服务时间归类出现频(次)数
服务时间(分)
出现频数(fi)
0~
55
15~
36
, 百拇医药
30~
17
45~
4
60~
1
75以上
0
合计
113
二、拟合检验
系统的统计推断,采用拟合优度的χ2检验,判定给定的排队系统符合那种分布模型。
, 百拇医药
(一)单位时间内到达的患者服从possion分布的拟合检验见表3:
单位时间患者平均到达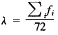
计算概率
计算理论频数
求χ2值 表3 单位时间内到达的患者数服从possion分布的χ2拟合检验
表3 单位时间内到达的患者数服从possion分布的χ2拟合检验
患者数
, 百拇医药
(i)
实际频数
(fi)
理论频数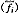
概率
(Pi)

0
24
27.61
, 百拇医药
0.3835
13.0630
0.4731
1
33
26.46
0.3676
42.7235
1.6144
2
10
12.68
0.1761
, 百拇医药
7.1851
0.5666
3
4
4.05
0.0563
0.0026
0.0006
≥4
1
0.97
0.0135
0.0009
, 百拇医药
0.0009
合计
72
λ=0.0958人/分
χ2=2.6556
取α=0.05,v=5-2=3时,查界值表χ20.05,3=7.81,χ2<χ20.05,3,P>0.05。该单位时间内的患者到达人数服从参数为0.0958的possion分布。
(二)服务时间服从负指数分布的拟合检验见表4:
每次检查平均服务时间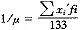
, 百拇医药
式中xi′为组中值
计算概率:
计算理论频数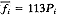
求χ2值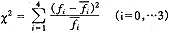 表4 服务时间服从负指数分布的χ2拟合检验
表4 服务时间服从负指数分布的χ2拟合检验
服务时间
(分)
实际频数
(fi)
, http://www.100md.com
理论频数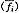
概率
(Pi)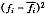
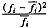
0~
55
61.44
0.5438
41.5271
0.6759
, http://www.100md.com
15~
36
28.03
0.2481
63.4623
2.2638
30~
17
12.29
0.1132
17.7219
1.3856
45~75
, 百拇医药
5
8.50
0.0752
12.2356
1.4398
合计
113
μ=0.0523人/分
χ2=5.7650
取α=0.05,v=4-2=2时,查界值表χ20.05,2=5.99,χ2<χ20.05,2,P>0.05。服务时间μ=0.0523的负指数分布。
, http://www.100md.com
三、求解与结果
由以上拟合优度的χ2检验知,该系统符合排队论中的M/M/C/∞/∞/FCFS型情形的排队模型,应用其计算公式得各项指标:λ=0.0958;μ=0.0523;C=3。
服务强度:
空闲概率: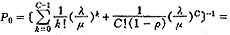

等待检查的平均患者人数:
系统中平均逗留患者数:
, 百拇医药
患者平均等待时间: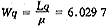
患者平均逗留时间:
系统满员率:
患者到达后必须等待的概率,也称超员率(即系统中患者数已有3人,各服务台没有空闲时):
四、结论与系统最优化
(一)根据以上结果知,该服务机构平均利用率61%,空闲概率14%,满员率14%,说明仪器的充分利用与2、4、5台B超仪的情形(见表5)相比最好的,患者平均等待时间6分钟,在B超室平均逗留25分钟,有50%以上患者到达后需等待,系统较为忙碌,难以保证服务质量,特别是系统发生意外(如某台设备故障)时,需长时间排队(见表5)。将设备增加至5台,各项指标虽有明显改善,但设备利用率仅36.6%,显然造成一定浪费。综上所述,4台B超仪是该系统的最优选择。表5 不同服务台数下各台的运行值
, 百拇医药
台
数
服务
强度
ρ
空闲
概率
P0
等待
人数
Lq
逗留
人数
, http://www.100md.com Ls
等待
时间
Wq
逗留
时间
Ws
满员率
P(n=C)
2
0.9159
0.0439
9.5327
, 百拇医药
11.3640
99.5060
118.630
0.0737
3
0.6106
0.1401
0.5776
2.4094
6.0297
25.150
0.1435
, http://www.100md.com 4
0.4579
0.1563
0.1142
1.9460
1.1925
20.313
0.0733
5
0.3663
0.1594
0.0250
1.8567
, 百拇医药
0.2609
19.381
0.0274
注:到达后需等待概率P(n>C):0.8757、0.3684、0.1352、0.0432
(二)①应用排队论,用运筹科学的理论和方法,对服务机构进行定量分析、评价,优化服务系统质量,提高服务效率,为设备的合理配置和有效利用提供科学依据。是进行布局规划和可行性分析的有效途径之一。②服务机构设备和人员配置,从患者和医院两者取得平衡出发,我们计算了4种情况的主要运行指标,以便比较,提出了该服务系统的最优选择。③提高服务水平,虽然降低了患者的等待费用,但增加了服务机构的成本。可以利用经济分析的手段,使二者费用之和为最小或使纯收入、利润为最大,但这要对服务费用(成本)、等待费用(损失)作确切估计。
作者单位:410013 长沙,湖南医科大学附属第三医院
(收稿:1999-01-21), http://www.100md.com
单位:410013 长沙,湖南医科大学附属第三医院
关键词:
中华医院管理杂志991032

中华医院管理杂志
CHINESE JOURNAL OF
HOSPITAL ADMINISTRATION
1999年 第15卷 第10期 Vol.15 No.10 1999

, 百拇医药
多服务台负指数分布排队系统在设备管理中的应用
郭才宁 李胜利
排队论,也称随机服务系统理论。排队是在日常生活中经常遇到的现象,在医院中,目前要求服务的数量通常都超过服务机构的容量。对服务系统进行定量分析,综合平衡患者与服务机构的设置,以期提高服务质量。
一、资料来源与方法
(一)根据我院超声科的调查,应用排队论的理论和方法评价与优化该服务系统。超声科有3台B超仪,机构形式是单队——多服务台的情形,服务时间是随机的,服务时间的分布假定平稳,即分布的参数不受时间的影响。调查内容是单位时间内到达的患者数与服务时间。
(二)单位时间内到达的患者数:每10分钟为一个调查单位,随机调查72个调查单位,记录每个调查单位内到达的患者数,结果见表1:
, 百拇医药
表1 单位调查时间的患者人数及频度
患者数(i)
出现的频数(fi)
0
24
1
33
2
10
3
4
4
1
, 百拇医药
5
0
合计
72
(三)服务时间:从为患者开始做B超检查(包括准备工作)时记起,到患者做完检查离去为止,随机调查113个患者的服务时间。不同服务时间的出现频(次)数见表2:表2 为每位患者服务时间归类出现频(次)数
服务时间(分)
出现频数(fi)
0~
55
15~
36
, 百拇医药
30~
17
45~
4
60~
1
75以上
0
合计
113
二、拟合检验
系统的统计推断,采用拟合优度的χ2检验,判定给定的排队系统符合那种分布模型。
, 百拇医药
(一)单位时间内到达的患者服从possion分布的拟合检验见表3:
单位时间患者平均到达
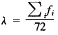
计算概率

计算理论频数

求χ2值
 表3 单位时间内到达的患者数服从possion分布的χ2拟合检验
表3 单位时间内到达的患者数服从possion分布的χ2拟合检验患者数
, 百拇医药
(i)
实际频数
(fi)
理论频数
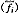
概率
(Pi)


0
24
27.61
, 百拇医药
0.3835
13.0630
0.4731
1
33
26.46
0.3676
42.7235
1.6144
2
10
12.68
0.1761
, 百拇医药
7.1851
0.5666
3
4
4.05
0.0563
0.0026
0.0006
≥4
1
0.97
0.0135
0.0009
, 百拇医药
0.0009
合计
72
λ=0.0958人/分
χ2=2.6556
取α=0.05,v=5-2=3时,查界值表χ20.05,3=7.81,χ2<χ20.05,3,P>0.05。该单位时间内的患者到达人数服从参数为0.0958的possion分布。
(二)服务时间服从负指数分布的拟合检验见表4:
每次检查平均服务时间
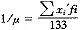
, 百拇医药
式中xi′为组中值
计算概率:

计算理论频数
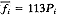
求χ2值
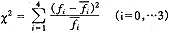 表4 服务时间服从负指数分布的χ2拟合检验
表4 服务时间服从负指数分布的χ2拟合检验服务时间
(分)
实际频数
(fi)
, http://www.100md.com
理论频数
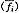
概率
(Pi)
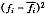
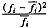
0~
55
61.44
0.5438
41.5271
0.6759
, http://www.100md.com
15~
36
28.03
0.2481
63.4623
2.2638
30~
17
12.29
0.1132
17.7219
1.3856
45~75
, 百拇医药
5
8.50
0.0752
12.2356
1.4398
合计
113
μ=0.0523人/分
χ2=5.7650
取α=0.05,v=4-2=2时,查界值表χ20.05,2=5.99,χ2<χ20.05,2,P>0.05。服务时间μ=0.0523的负指数分布。
, http://www.100md.com
三、求解与结果
由以上拟合优度的χ2检验知,该系统符合排队论中的M/M/C/∞/∞/FCFS型情形的排队模型,应用其计算公式得各项指标:λ=0.0958;μ=0.0523;C=3。
服务强度:

空闲概率:
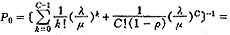

等待检查的平均患者人数:

系统中平均逗留患者数:

, 百拇医药
患者平均等待时间:
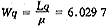
患者平均逗留时间:

系统满员率:

患者到达后必须等待的概率,也称超员率(即系统中患者数已有3人,各服务台没有空闲时):

四、结论与系统最优化
(一)根据以上结果知,该服务机构平均利用率61%,空闲概率14%,满员率14%,说明仪器的充分利用与2、4、5台B超仪的情形(见表5)相比最好的,患者平均等待时间6分钟,在B超室平均逗留25分钟,有50%以上患者到达后需等待,系统较为忙碌,难以保证服务质量,特别是系统发生意外(如某台设备故障)时,需长时间排队(见表5)。将设备增加至5台,各项指标虽有明显改善,但设备利用率仅36.6%,显然造成一定浪费。综上所述,4台B超仪是该系统的最优选择。表5 不同服务台数下各台的运行值
, 百拇医药
台
数
服务
强度
ρ
空闲
概率
P0
等待
人数
Lq
逗留
人数
, http://www.100md.com Ls
等待
时间
Wq
逗留
时间
Ws
满员率
P(n=C)
2
0.9159
0.0439
9.5327
, 百拇医药
11.3640
99.5060
118.630
0.0737
3
0.6106
0.1401
0.5776
2.4094
6.0297
25.150
0.1435
, http://www.100md.com 4
0.4579
0.1563
0.1142
1.9460
1.1925
20.313
0.0733
5
0.3663
0.1594
0.0250
1.8567
, 百拇医药
0.2609
19.381
0.0274
注:到达后需等待概率P(n>C):0.8757、0.3684、0.1352、0.0432
(二)①应用排队论,用运筹科学的理论和方法,对服务机构进行定量分析、评价,优化服务系统质量,提高服务效率,为设备的合理配置和有效利用提供科学依据。是进行布局规划和可行性分析的有效途径之一。②服务机构设备和人员配置,从患者和医院两者取得平衡出发,我们计算了4种情况的主要运行指标,以便比较,提出了该服务系统的最优选择。③提高服务水平,虽然降低了患者的等待费用,但增加了服务机构的成本。可以利用经济分析的手段,使二者费用之和为最小或使纯收入、利润为最大,但这要对服务费用(成本)、等待费用(损失)作确切估计。
作者单位:410013 长沙,湖南医科大学附属第三医院
(收稿:1999-01-21), http://www.100md.com