中医阴阳学说的一个数学模型
作者：翟忠信
单位：兰州大学数学系 兰州730000
关键词：阴阳学说；微分方程 平衡点；生物数学；电脑
数理医药学杂志990407
摘 要 提出了一个描述中医阴阳关系的动态数学模型。通过对这一模型稳定性的分析，较好地解释了由机体阴阳状态的变化所产生的多种病理现象，并说明了在某些特定情况下所应采取的治疗方法及其临床意义。
1 引言
阴阳学说是中医学的指导理论之一。《素问.阴阳应象大论》说：“阴阳者，天地之道也，万物之纲纪，变化之父母，生杀之本始，神明之府也。”阴阳学说贯穿在中医理论的各个方面，用来说明人体的组织结构，生理功能，疾病的发生发展规律，并指导临床诊断和治疗[1]。
, 百拇医药
阴阳学说的基本内容是两个抽象概念“阴”和“阳”的对立统一性。这一对立统一性主要表现于下列三个方面：
①互惠关系(包括互根关系)；②互消关系；③消长关系。
有的作者还提出阴阳之间有着转化关系，我们这里暂时把转化关系看成上三种关系的结果，不再单独列出。
千百年来，中医学家都在依据自己的经验和理解，定性地运用着阴阳关系的这几个方面，来解释各种生理病理现象，指导临床实践。但由于经典的中医学理论对这几种关系向来是叙述得过于笼统，以至于看上去似乎存在着相互矛盾之处：当机体阴阳处于某种不平衡状态时，随着时间的推移，依互惠关系，应趋于阴阳两旺(或两亢)；依互消关系，应趋于阴阳两衰；而依消长关系，又应趋于阴盛阳衰或阳胜阴衰。况且，阴阳两旺既可以说是“生机旺盛”之好事，而“亢乃害，承乃治”，则又可以说是一种病态了。这些矛盾现象，大量见于古今多种医学文献，乃至一些医家各执一端，互相排斥，争论不休。
, 百拇医药
实际上，这三条关系并不是对任何个体的任何阴阳状态都同时起着同样大的作用，而是对不同的个体、不同阴阳状态、在不同的时机，可能这条或那条关系起主导作用，其它两种作用处于相对次要的地位；而这一主导作用对机体的影响是好是坏，也要视具体情形而定。要想很好地说明这些问题，就需要建立一个关于阴阳学说的数学模型。
2 数学模型的提出
设在平面直角坐标系xoy中，以x轴表示“阴”，以y轴表示“阳”，则在坐标平面上第一象限及两个正半轴连同坐标原点所构成的一个点集R中的任一点P(x,y)，均可表示机体的一个阴阳状态(或称健康状态，下简称状态)。其中x≥0表示“阴”的量值的大小，而y≥0则表示“阳”的量值的大小(按照中医学的观点，人生有形，不离阴阳”，故设x≥0,y≥0)。
人体在不同时刻的状态不尽相同，故x,y也应随时间而变。设x,y均为时间t的连续可微函数，并分别以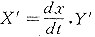
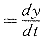表阴阳二变量对时间的变化率。依照中医学的成论和一般的医学常识，我们首先给出如下几条假设：
, 百拇医药
2.1 R中有一个理想的阴阳平衡点A(x0,y0),当机体的状态P(x,y)离开此平衡点，但仍处于以此平衡点为内点的一个有界单连通域△0内时，由阴阳的相互作用，随着时间的推移，机体状态可自动恢复到平衡点，我们称这样的区域△0为健康区。
2.2 在△之外，有一个包围△0的环形区域△1，当机体状态处于此△1内时，阴阳失去平衡，且已不能自动恢复到其平衡位置A(x0,y0)(当然，并不排除可籍助药物的作用使机体的阴阳状态返回到健康区)，但由于阴阳的相互作用可使机体状态稳定在一个新的非健康位置B(x1,y1)上。我们称△1为代偿区，称B为病态平衡点。
2.3 当机体状态离开平衡点A更远，即处于△0∪△1的闭包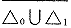
之外时，机体的状态只可能逐渐恶化。把这一现象用数学语言来描述，就是当时间变量t→+∞时，x或y→0或+∞，即机体走向死亡。我们称着一区域为恶化区，记为△2，即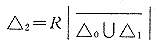
, http://www.100md.com
2.4 当x或y有一个为零时，x,y不再随时间变化。
为得到满足上述四条假设的数学模型，我们再引进如下记号：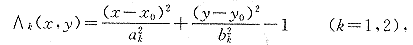
Φ(x,y)≡(x-x0)2+(y-y0)2-r2,Ψ(x,y)≡(x-x0)2+(y-y0)2-R2,其中的参数x0>0,y0>0,而a1,a2,b1,b2,r和R间满足关系
01,a2,b1,b2}≤max{a1,a2,b1,b2}
于是二维欧氏空间中的微分方程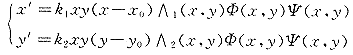
(1)
就是我们所提出的描述机体阴阳变化规律的一个数学模型，其中k1,k2均为正常数。显然，(1)是一个二维自治系统。
3 稳定性分析与中医学的解释
x＇与y＇的符号的不同组合，对应着阴阳间的不同关系，且可依此大体确定方程(1)的轨线走向，见下表。 X＇
Y＇
阴阳关系
轨线走向
+
, http://www.100md.com
+
阴阳互惠
+
-
阴长阳消
-
+
阴消阳长
-
-
, http://www.100md.com
阴阳互消
再根据a1和a2，b1和b2的大小关系，又可分出九种情形：
① a12,b12; ② a1>a2,b1>b2;
③ a12,b1>b2; ④ a1>a2,b12;
, http://www.100md.com ⑤ a1=a2,b1=b2; ⑥ a1=a2,b12;
⑦ a1=a2,b1>b2; ⑧ a12,b1=b2;
⑨ a1>a2,b1=b2
下面，我们在图1、图2、和图3中画出了①、④、⑤几种情形下方程(1)的轨线，大体标出轨线走向，由此分出了三个区域△1，△2和△3，并指出诸平衡点的性质。图中标记的几条封闭曲线分别是
, 百拇医药
Lk：∧k(x,y)=0 (k=1,2)；
Γ1:Φ(x,y)=0;Γ2:Ψ(x,y)=0
由此再对照前面所提出的四条假设，容易看出它们的中医学意义。
在上述诸情形中，A(x0,y0)均为稳定结点，坐标轴x=0,y=0及曲线Γ1,Γ2均为奇线。健康区均为小圆Γ1内部的区域
△0={(x,y)|Φ(x,y)<0}
代偿区均为两个圆周Γ1和Γ2之间的区域
, http://www.100md.com
△1={(x,y)|r2<(x-x0)2+(y-y0)22}={(x,y)|Φ(x,y)>0,Ψ(x,y)<0}
恶化区均为大圆Γ2外部的区域
△2={(x,y)|Ψ(x-y)>0}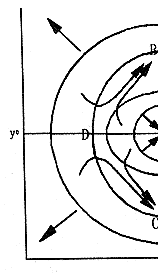
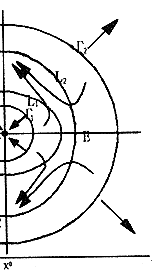
图1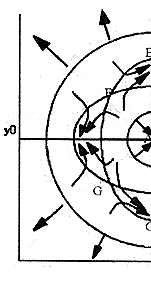
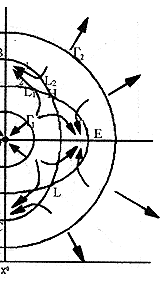
, http://www.100md.com
图2
图1中，A、B、C是稳定结点，D、E是鞍点。
图2中，A、B、C、D、E是稳定结点，F、G、H、L是鞍点[2,3]。
下面我们只对图2和图3做较为详细的中医学解释，图1可仿照图2的情形来理解。
由图2可见，当机体状态处于健康区时，通过阴阳的互惠(见小圆△0的左下部)、互消(见小圆△0的右上部)和消长(见小圆△0的左上部及右下部)三种关系的作用，可使机体自动趋于平衡位置A，这时，阴阳间的三种关系所起的作用可以说都是好作用。
当机体状态处于恶化区△2时，由阴阳间三条关系的作用，可使机体状态进一步恶化，直至趋于死亡。此时这三条关系所起的作用，又可以说都是坏作用了。
, http://www.100md.com
当机体状态处于带偿区△1时，可使机体在新的基础上达到新的平衡：当阳较盛时，平衡于B点(此点阳盛阴平，这时的机体变成一种相对阳盛的体质了)；阳较衰时，平衡于点C(阳衰阴平相对阳衰体质)；阴较盛量，平衡于点E(阴盛阳平相对阴盛体质)；阴较弱时，平衡于点D(阴衰阳平相对阴衰体质)。这时阴阳三关系的作用，虽不能使机体完全康复，但也可避免其无限的恶化，至于这些作用是好是坏，需做具体分析方知。如图2之轨线1上，x(阴)一直在趋于x0(平衡位置)，但y(阳)先是向y0(平衡点)行进，当经过L2时，突然掉头转向远离y0，遂使轨线趋于病态点B。故开始时轨线上所体现出来的阴阳相消作用可以说是一种好作用，而后y由降变为升，而使阴阳关系变为消长(阴消阳长)关系，便是坏现象了。但x的“表现”一直是好的。对其它始于△1的轨线，亦可作如是分析。
图3所表示的是a1=a2,b1=b2的一个极端情形。这时曲线L=L1=L2上的点全是平衡点，这些平衡点均非孤立，L形成一条奇线。当机体阴阳状态P处于代偿区△1时，随着时间的推移，可平衡于L上的任一位置，较简单直观的解释了上面所提出的四条假设。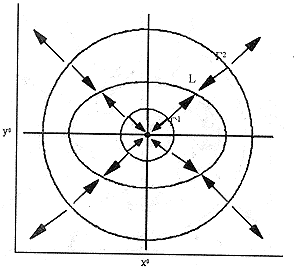
, 百拇医药
图3
值得注意的是，这些病态平衡点都是不稳定平衡点，可以认为是病情暂时所处的一种非正常状态。由于它的不稳定性，随机体机能状态的少许变化或外邪的侵袭，疾病又将处于活动状态。
图4是在特殊条件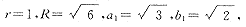
a2=2,b2=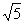
k1=k2=1,x0=y0=2.5
下，由电脑(籍助MathCad Plus 6.0软件，使用Runge-Kutta法叠代)自动描绘出的方程组(*)的几条轨线L*1,L*2,L*3,它们所对应的初始条件分别是：
, http://www.100md.com
L*1:x0=0.4, y0=1.4
L*2:x0=3.4, y0=2.9
L*3:x0=3.5, y0=3
和图1中同一位置的线条相对照，可进一步验证我们关于模型稳定性的分析。从图4还可以看出，是然L*1和L*2的初始条件所代表的同是阴阳两盛的病情，只是稍有量的区别，但是疾病的归转却大不相同：一个病情逐渐恶化，直到稳定于某个病态平衡点，变成阴平阳盛体质(L*3)；另一个则完全康复(L*2)。这一点，只有通过数学模型，才能解释得清楚。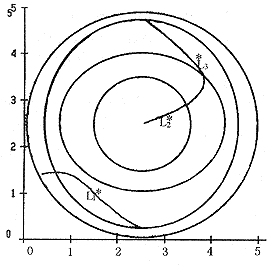
, http://www.100md.com
图4
4 几点说明
上面我们假定了参k1,k2,a1,a2,b1,b2,r,R均为常数，即(*)是一个自治系统，并把L1,L2处理为两个椭圆，把Γ1,Γ2处理为两个圆周，这完全是为了方便。实际上，这些参数也应随时间而变，是时间t的函数。正是这些参数的变化，才导致机体整个健康状态和体质的改变。而且，L1,L2,Γ1,Γ2也可用其它曲线代替，只要不改变它们的相对位置。而药物对机体作用的一个重要方面，也正是通过改变这些参数的值以及改变几条曲线的形状，实现机体阴阳状态的相对运动，使之从恶化区变到代偿区，从代偿区变到健康区的。外邪对机体的作用则与之恰恰相反。
, 百拇医药
设机体原来处于某健康状态P∈△0，由于外邪的作用，使之(相对地)变到另一点Q。这时因体质的不同，健康状态的差异，可出现各种现象：当健康状态较佳(△0较大)时，Q仍处于△0之中，机体不受病；反之，若机体健康状态极差(△0极小)，使点Q变到恶化区△2，倘不及时治疗，机体将趋于死亡。当健康状况一般，或外邪的强度适中，使Q∈△1，即阴阳状态位于代偿区时，视体质的差异，机体将患程度不同(有时甚至是性质不同)的疾病，且受病后，Q将随时间而运动，直至最后平衡于某个病态点，如结核病之钙化，即属此种类型。
所谓“急则治其标”，可理解为通过药物或其它治疗措施，移动Q的位置，使之从△1变到△0，这时健康区△0的大小不一定增加，甚至还有可能减小。“缓则治其本”的思想则不然，它主要是通过扩大健康区△0，使原来本不属于△0的点Q包含于其中，进而通过机体自身的作用，使其阴阳状态趋于相对平衡，这最终的结果，不但疾病得以治愈，而且机体的健康状态得到了增强。
, http://www.100md.com
当然，视具体情形，可把x视为血、寒、里、虚,同时把y视为气、热、表、实等等。
本文所分出的九种机体状态，也可代表九种体质[4]，如《内经.阴阳二十五人》中关于“五态人”的分类那样。
最后要说明的是，本文所提出的模型(1)，充分借鉴了生物数学中关于两种群相互作用的数学模型[5]。目前，生物数学已发展成为自然科学的一个强有力的分支。我国数千年前就已成熟了的中医阴阳学说，竟然和这么精密的现代学科相一致，而且它们居然吻合得这样好，以至于毫无牵强附会之处，这本身就是一个奇迹。可以说，它们一个是“远及于物”，研究自然界的物种现象，一个是“近及于身”，探讨人体的生理机制，两者互为表里，也可以说，它们是自然辩证法这一普遍真理在不同领域的具体体现。因此，我们希望本文能引起广大的数学工作者对中医理论的关注。
, 百拇医药 参考文献
1 张珍玉主编.实用中医基础理论.山东科技出版社，1985，38～52,45.
2 H.I.Fredoman. Deterministic Mathematical Model in Population Ecology, Marcel. Dekker. Inc. New York and Basel. 1980,74～78.
3 张锦炎.常微分方程几何理论与分支问题.北京大学出版社，1987(再版)，20～38.
4 王其庆，钱承辉.中医脏象学.上海中医学院出版社，1987，200～220.
5 陈兰荪.数学生态学模型与研究方法.科学出版社，1988，129～232.
收稿日期：1999-01-25, http://www.100md.com
单位：兰州大学数学系 兰州730000
关键词：阴阳学说；微分方程 平衡点；生物数学；电脑
数理医药学杂志990407
摘 要 提出了一个描述中医阴阳关系的动态数学模型。通过对这一模型稳定性的分析，较好地解释了由机体阴阳状态的变化所产生的多种病理现象，并说明了在某些特定情况下所应采取的治疗方法及其临床意义。
1 引言
阴阳学说是中医学的指导理论之一。《素问.阴阳应象大论》说：“阴阳者，天地之道也，万物之纲纪，变化之父母，生杀之本始，神明之府也。”阴阳学说贯穿在中医理论的各个方面，用来说明人体的组织结构，生理功能，疾病的发生发展规律，并指导临床诊断和治疗[1]。
, 百拇医药
阴阳学说的基本内容是两个抽象概念“阴”和“阳”的对立统一性。这一对立统一性主要表现于下列三个方面：
①互惠关系(包括互根关系)；②互消关系；③消长关系。
有的作者还提出阴阳之间有着转化关系，我们这里暂时把转化关系看成上三种关系的结果，不再单独列出。
千百年来，中医学家都在依据自己的经验和理解，定性地运用着阴阳关系的这几个方面，来解释各种生理病理现象，指导临床实践。但由于经典的中医学理论对这几种关系向来是叙述得过于笼统，以至于看上去似乎存在着相互矛盾之处：当机体阴阳处于某种不平衡状态时，随着时间的推移，依互惠关系，应趋于阴阳两旺(或两亢)；依互消关系，应趋于阴阳两衰；而依消长关系，又应趋于阴盛阳衰或阳胜阴衰。况且，阴阳两旺既可以说是“生机旺盛”之好事，而“亢乃害，承乃治”，则又可以说是一种病态了。这些矛盾现象，大量见于古今多种医学文献，乃至一些医家各执一端，互相排斥，争论不休。
, 百拇医药
实际上，这三条关系并不是对任何个体的任何阴阳状态都同时起着同样大的作用，而是对不同的个体、不同阴阳状态、在不同的时机，可能这条或那条关系起主导作用，其它两种作用处于相对次要的地位；而这一主导作用对机体的影响是好是坏，也要视具体情形而定。要想很好地说明这些问题，就需要建立一个关于阴阳学说的数学模型。
2 数学模型的提出
设在平面直角坐标系xoy中，以x轴表示“阴”，以y轴表示“阳”，则在坐标平面上第一象限及两个正半轴连同坐标原点所构成的一个点集R中的任一点P(x,y)，均可表示机体的一个阴阳状态(或称健康状态，下简称状态)。其中x≥0表示“阴”的量值的大小，而y≥0则表示“阳”的量值的大小(按照中医学的观点，人生有形，不离阴阳”，故设x≥0,y≥0)。
人体在不同时刻的状态不尽相同，故x,y也应随时间而变。设x,y均为时间t的连续可微函数，并分别以
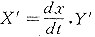
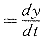表阴阳二变量对时间的变化率。依照中医学的成论和一般的医学常识，我们首先给出如下几条假设：, 百拇医药
2.1 R中有一个理想的阴阳平衡点A(x0,y0),当机体的状态P(x,y)离开此平衡点，但仍处于以此平衡点为内点的一个有界单连通域△0内时，由阴阳的相互作用，随着时间的推移，机体状态可自动恢复到平衡点，我们称这样的区域△0为健康区。
2.2 在△之外，有一个包围△0的环形区域△1，当机体状态处于此△1内时，阴阳失去平衡，且已不能自动恢复到其平衡位置A(x0,y0)(当然，并不排除可籍助药物的作用使机体的阴阳状态返回到健康区)，但由于阴阳的相互作用可使机体状态稳定在一个新的非健康位置B(x1,y1)上。我们称△1为代偿区，称B为病态平衡点。
2.3 当机体状态离开平衡点A更远，即处于△0∪△1的闭包
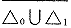之外时，机体的状态只可能逐渐恶化。把这一现象用数学语言来描述，就是当时间变量t→+∞时，x或y→0或+∞，即机体走向死亡。我们称着一区域为恶化区，记为△2，即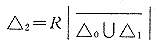, http://www.100md.com
2.4 当x或y有一个为零时，x,y不再随时间变化。
为得到满足上述四条假设的数学模型，我们再引进如下记号：
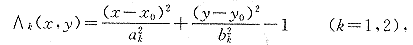
Φ(x,y)≡(x-x0)2+(y-y0)2-r2,Ψ(x,y)≡(x-x0)2+(y-y0)2-R2,其中的参数x0>0,y0>0,而a1,a2,b1,b2,r和R间满足关系
0
于是二维欧氏空间中的微分方程
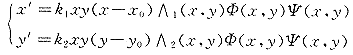(1)就是我们所提出的描述机体阴阳变化规律的一个数学模型，其中k1,k2均为正常数。显然，(1)是一个二维自治系统。
3 稳定性分析与中医学的解释
x＇与y＇的符号的不同组合，对应着阴阳间的不同关系，且可依此大体确定方程(1)的轨线走向，见下表。 X＇
Y＇
阴阳关系
轨线走向
+
, http://www.100md.com
+
阴阳互惠
+
-
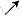
阴长阳消
-
+
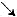
阴消阳长
-
-
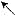
, http://www.100md.com
阴阳互消
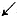
再根据a1和a2，b1和b2的大小关系，又可分出九种情形：
① a1
③ a1
, http://www.100md.com ⑤ a1=a2,b1=b2; ⑥ a1=a2,b1
⑦ a1=a2,b1>b2; ⑧ a1
⑨ a1>a2,b1=b2
下面，我们在图1、图2、和图3中画出了①、④、⑤几种情形下方程(1)的轨线，大体标出轨线走向，由此分出了三个区域△1，△2和△3，并指出诸平衡点的性质。图中标记的几条封闭曲线分别是
, 百拇医药
Lk：∧k(x,y)=0 (k=1,2)；
Γ1:Φ(x,y)=0;Γ2:Ψ(x,y)=0
由此再对照前面所提出的四条假设，容易看出它们的中医学意义。
在上述诸情形中，A(x0,y0)均为稳定结点，坐标轴x=0,y=0及曲线Γ1,Γ2均为奇线。健康区均为小圆Γ1内部的区域
△0={(x,y)|Φ(x,y)<0}
代偿区均为两个圆周Γ1和Γ2之间的区域
, http://www.100md.com
△1={(x,y)|r2<(x-x0)2+(y-y0)2
恶化区均为大圆Γ2外部的区域
△2={(x,y)|Ψ(x-y)>0}
图1
, http://www.100md.com
图2
图1中，A、B、C是稳定结点，D、E是鞍点。
图2中，A、B、C、D、E是稳定结点，F、G、H、L是鞍点[2,3]。
下面我们只对图2和图3做较为详细的中医学解释，图1可仿照图2的情形来理解。
由图2可见，当机体状态处于健康区时，通过阴阳的互惠(见小圆△0的左下部)、互消(见小圆△0的右上部)和消长(见小圆△0的左上部及右下部)三种关系的作用，可使机体自动趋于平衡位置A，这时，阴阳间的三种关系所起的作用可以说都是好作用。
当机体状态处于恶化区△2时，由阴阳间三条关系的作用，可使机体状态进一步恶化，直至趋于死亡。此时这三条关系所起的作用，又可以说都是坏作用了。
, http://www.100md.com
当机体状态处于带偿区△1时，可使机体在新的基础上达到新的平衡：当阳较盛时，平衡于B点(此点阳盛阴平，这时的机体变成一种相对阳盛的体质了)；阳较衰时，平衡于点C(阳衰阴平相对阳衰体质)；阴较盛量，平衡于点E(阴盛阳平相对阴盛体质)；阴较弱时，平衡于点D(阴衰阳平相对阴衰体质)。这时阴阳三关系的作用，虽不能使机体完全康复，但也可避免其无限的恶化，至于这些作用是好是坏，需做具体分析方知。如图2之轨线1上，x(阴)一直在趋于x0(平衡位置)，但y(阳)先是向y0(平衡点)行进，当经过L2时，突然掉头转向远离y0，遂使轨线趋于病态点B。故开始时轨线上所体现出来的阴阳相消作用可以说是一种好作用，而后y由降变为升，而使阴阳关系变为消长(阴消阳长)关系，便是坏现象了。但x的“表现”一直是好的。对其它始于△1的轨线，亦可作如是分析。
图3所表示的是a1=a2,b1=b2的一个极端情形。这时曲线L=L1=L2上的点全是平衡点，这些平衡点均非孤立，L形成一条奇线。当机体阴阳状态P处于代偿区△1时，随着时间的推移，可平衡于L上的任一位置，较简单直观的解释了上面所提出的四条假设。
, 百拇医药
图3
值得注意的是，这些病态平衡点都是不稳定平衡点，可以认为是病情暂时所处的一种非正常状态。由于它的不稳定性，随机体机能状态的少许变化或外邪的侵袭，疾病又将处于活动状态。
图4是在特殊条件
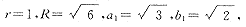
a2=2,b2=
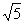
k1=k2=1,x0=y0=2.5
下，由电脑(籍助MathCad Plus 6.0软件，使用Runge-Kutta法叠代)自动描绘出的方程组(*)的几条轨线L*1,L*2,L*3,它们所对应的初始条件分别是：
, http://www.100md.com
L*1:x0=0.4, y0=1.4
L*2:x0=3.4, y0=2.9
L*3:x0=3.5, y0=3
和图1中同一位置的线条相对照，可进一步验证我们关于模型稳定性的分析。从图4还可以看出，是然L*1和L*2的初始条件所代表的同是阴阳两盛的病情，只是稍有量的区别，但是疾病的归转却大不相同：一个病情逐渐恶化，直到稳定于某个病态平衡点，变成阴平阳盛体质(L*3)；另一个则完全康复(L*2)。这一点，只有通过数学模型，才能解释得清楚。
, http://www.100md.com
图4
4 几点说明
上面我们假定了参k1,k2,a1,a2,b1,b2,r,R均为常数，即(*)是一个自治系统，并把L1,L2处理为两个椭圆，把Γ1,Γ2处理为两个圆周，这完全是为了方便。实际上，这些参数也应随时间而变，是时间t的函数。正是这些参数的变化，才导致机体整个健康状态和体质的改变。而且，L1,L2,Γ1,Γ2也可用其它曲线代替，只要不改变它们的相对位置。而药物对机体作用的一个重要方面，也正是通过改变这些参数的值以及改变几条曲线的形状，实现机体阴阳状态的相对运动，使之从恶化区变到代偿区，从代偿区变到健康区的。外邪对机体的作用则与之恰恰相反。
, 百拇医药
设机体原来处于某健康状态P∈△0，由于外邪的作用，使之(相对地)变到另一点Q。这时因体质的不同，健康状态的差异，可出现各种现象：当健康状态较佳(△0较大)时，Q仍处于△0之中，机体不受病；反之，若机体健康状态极差(△0极小)，使点Q变到恶化区△2，倘不及时治疗，机体将趋于死亡。当健康状况一般，或外邪的强度适中，使Q∈△1，即阴阳状态位于代偿区时，视体质的差异，机体将患程度不同(有时甚至是性质不同)的疾病，且受病后，Q将随时间而运动，直至最后平衡于某个病态点，如结核病之钙化，即属此种类型。
所谓“急则治其标”，可理解为通过药物或其它治疗措施，移动Q的位置，使之从△1变到△0，这时健康区△0的大小不一定增加，甚至还有可能减小。“缓则治其本”的思想则不然，它主要是通过扩大健康区△0，使原来本不属于△0的点Q包含于其中，进而通过机体自身的作用，使其阴阳状态趋于相对平衡，这最终的结果，不但疾病得以治愈，而且机体的健康状态得到了增强。
, http://www.100md.com
当然，视具体情形，可把x视为血、寒、里、虚,同时把y视为气、热、表、实等等。
本文所分出的九种机体状态，也可代表九种体质[4]，如《内经.阴阳二十五人》中关于“五态人”的分类那样。
最后要说明的是，本文所提出的模型(1)，充分借鉴了生物数学中关于两种群相互作用的数学模型[5]。目前，生物数学已发展成为自然科学的一个强有力的分支。我国数千年前就已成熟了的中医阴阳学说，竟然和这么精密的现代学科相一致，而且它们居然吻合得这样好，以至于毫无牵强附会之处，这本身就是一个奇迹。可以说，它们一个是“远及于物”，研究自然界的物种现象，一个是“近及于身”，探讨人体的生理机制，两者互为表里，也可以说，它们是自然辩证法这一普遍真理在不同领域的具体体现。因此，我们希望本文能引起广大的数学工作者对中医理论的关注。
, 百拇医药 参考文献
1 张珍玉主编.实用中医基础理论.山东科技出版社，1985，38～52,45.
2 H.I.Fredoman. Deterministic Mathematical Model in Population Ecology, Marcel. Dekker. Inc. New York and Basel. 1980,74～78.
3 张锦炎.常微分方程几何理论与分支问题.北京大学出版社，1987(再版)，20～38.
4 王其庆，钱承辉.中医脏象学.上海中医学院出版社，1987，200～220.
5 陈兰荪.数学生态学模型与研究方法.科学出版社，1988，129～232.
收稿日期：1999-01-25, http://www.100md.com