疾病的空间分布动态模型研究--疾病的空间动态分布模型研究(一)
作者:薛付忠 王洁贞
单位:山东医科大学公共卫生学院 济南250012
关键词:
数理医药学杂志990405
疾病的发生受多种因素的影响,由于时间不同、人群不同、地区不同,或其他条件的改变均可使疾病的流行规律发生变化。因此,必须以动态和变化的观点去认识疾病流行规律[1]。对疾病流行动态的研究包括三个方面:一是追踪流行强度随时间的变化,即所谓流行强度的时间动态问题;二是观察不同特征人群流行强度的变化,即所谓流行强度的人间动态问题;三是考察患病个体在空间散步状态的变化,即所谓空间动态问题。其中,对疾病空间动态的研究尤为重要,而目前又研究得不够深入。本研究从疾病生态学的观点出发,将生态学的基本原理和方法同流行病学、概率论与数理统计、系统论等相结合,提出了疾病空间分布动态模式的基本假设,在此假设下,以肾综合征出血热为研究对象,建立五大类表达疾病空间动态格局的一系列数学模型,这无论对丰富流行病学理论还是对制定切实可行的疾病防治措施都具有重要意义。本文是整个研究中的总论部分。
, 百拇医药
1 生态学的空间格局观点
按照生态学的观点,正确地表征生态系统的空间格局,并对其进行数量分析与比较,是判断区域生态平衡,追踪生态演变,评价生态系统干预措施效果的必要条件之一。任何生态系统类型,离开了它所处的空间格局,其它诸如环境与生物诸要素相互作用的问题,生态系统的发展与演变等问题,统统失去了讨论的基础。就某一特定的生态系统而言,尽管有较相似的非生物环境条件,该生态系统的空间格局仍会有明显的差异。至于对自然环境很不一致的地域,这种空间格局所表现出的差异就会更大。一般来说,空间结构上的差异,不仅影响生态系统的功能,最终将影响到该生态系统的总输出。从这个意义上讲,探求生态系统的空间结构规律,对于控制生态系统具有重要意义。对于疾病生态系统而言,同样存在着以上生态学的共性问题。因而,本研究将生态学的基本原理同概率论与数理统计相结合,根据疾病流行病学特点,提出以下流行病学假设,并以此假设建立疾病空间动态模型。
2 疾病空间格局类型及其动态的流行病学假设
, http://www.100md.com
疾病空间格局是指其在所处的特定生境空间中的结构,这种结构的形式是疾病对环境条件的适应或选择的结果。这里设想疾病的空间格局存在三种类型:
①随机格局 疾病病例个体之间相互独立,既无吸引也无排斥,病例间没有一定的流行病学联系。描述这种空间格局的概率模型是Poisson分布,其主要特征是s2= ,其中
,其中 是疾病病例的密度,即平均每个样本单位(样方)中的病例数,s2是相应样本的方差。
是疾病病例的密度,即平均每个样本单位(样方)中的病例数,s2是相应样本的方差。
②聚集格局 疾病病例个体间存在某种联系,在空间内出现聚块(patch)。描述这种空间格局的概率模型主要是集中邻接分布。如Γ-Poisson分布(负二项分布)、Poisson-Poisson分布(Neymans A型分布)、β-二项分布、Poisson-二项分布、带协变量的分布(如时依Poisson)、混合Poisson分布等,它们的共同特点是s2> 。
。
, http://www.100md.com
③均匀格局 假定在一特定生境中某病病例个体之间是相互排斥的,这种空间格局常用二项分布来描述。其特点是s2< 。
。
我们认为疾病的发生受诸多因素的影响,这些因素在不断地发生变化,因而病例无论取那种空间格局,都不是一成不变的。①、②、③三种格局之间乃至描述它们的概率分布之间并不是独立无关的。无论从疾病生态学或流行病学意义上还是从概率论与数理统计学意义上,病例的所有可能分布型组成了一个连续统(这是一个生态学术语,在此借用),其一端是均匀分布,另一端是高度聚集的分布,而Piosson分布则是这个连续统中间的一个过渡点。从时间上考虑,随着病例在一特定生境内的密度变化,其空间格局也不断变化着,于是就可能经历由Piosson分布经负二项分布或其他复合分布到某种高度偏态,拖尾很长的高聚集分布的动态过程。这些假设思想是符合疾病的实际发生与流行动态的,因而在此前提下,以流行病学和概率论与数理统计的理论为指导,应用生态学、系统论等领域研究的最新成果,对疾病空间动态进行系统研究,建立揭示其发生与流行的空间动态的各种数学模型,便可能会找到疾病发生与流行的本质规律。
, 百拇医药
3 空间动态模型建模方法
根据以上假设,本研究以山东省、山东省临沂市、临沂市所辖的平邑县的肾综合征出血热(HRFS)为研究对象,建立了一系列疾病空间分布动态的模型,现简介如下:
3.1 离散性频率模型
这类模型为离散性的空间动态模型,是在时间维上,用各种概率分布模型模拟病例的空间分布动态,从而揭示其流行规律。除用二项分布、Poisson分布等单一模型外,主要应用陈锋、杨树勤介绍的各种复合模型[1~6]。
3.2 Pearson-Ⅲ连续性空间分布模型[7,8]
由于疾病的发生是病因、宿主、环境三者共同作用的结果,所以其变化会很复杂。这里假设某病病例的空间分布特点是在时间维上变化较快,在一定时间时期可达到相当大的数量,一定范围内个体数变量的离散程度较高。在这种情况下,用前面介绍的离散型频率模型,就不合适,这是由于它们的变通性小,每种模型只是适用于特定的分布,参数信息少,分布的直观性差。为克服离散型频率模型的这些缺点,本研究将Pearson-Ⅲ连续性空间分布模型引入疾病空间动态研究获得满意效果。其基本方法是:对于某一特定生境,在时间维上(月份、季度、流行年),采用回顾性或前瞻性方法,连续观察若干次(n次)内某病病例的空间分布情况,或在同一时期内,同时观察若干个(n个)特定生境内某病病例的空间分布情况,各样本量由于取样时间或地点的约束和个体分布密度的不同而不相等。这些变量组成的样本可视为来自n个概率分布总体,把它们串起来可望得到对特定生境内某病病例概率分布的动态特点。
, http://www.100md.com
Pearson-Ⅲ连续性空间分布模型的概率函数为:
其中,α>0,β>0,x≥b,Pearson-Ⅲ连续性空间分布是一个三参数分布。其参数估计方法有矩法、适线法、极大似然法和单纯性法等。其空间分布判定指标及其流行病学含义为:
①
Q<1,聚集分布,Q越小聚集性越大;
Q=1,随机分布;
Q>1,均匀分布,Q越大分布越均匀。
②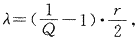 其中r=x20.5(2αQ2/(1-Q)β2
其中r=x20.5(2αQ2/(1-Q)β2
, 百拇医药
λ>2时,聚集由病例间存在着内在联系所引起,这种内在联系很可能反映了致病因子及环境因子的聚集性;
λ<2时,聚集由病例所处的地理环境决定,包括引起HRFS病例发生的若干环境因素的集合。
3.3 基于Taylor幂法则[9~12]的各种聚集尺度模型
我们假定某病病例在某一特定生境中的空间分布遵循下面一条概念性的空间分布规律:在某一特定生境内,病例的空间分布,总是以Poisson分布为基准,沿着两个相反的方向演化。其一,与Poisson分布相比,在二维空间内点的分布具有更为聚合,更加集族(灶性发病点)的趋势;其二,与Poisson分布相比在二维空间内点的分布具有更为分散、更加均匀的趋势(病例高度散发)。作为上述两种趋势的极端表现,前者所有的点均重叠地分布于一个唯一的面积单元(即样本单位)之中,可以看作几个相集在一起的高度聚合的特殊分布;而后者则是所有的点在一个二维空间内各占据相等的面积,即点均匀地排布于每一面积单元之中,它可以看作为各点距离之间完全相等的高度分散的特殊分布。由上述可以推论出,在点的空间分布的基本表述上,可以发现这些点的空间分布模式能够从完全聚合于一个唯一的面积单元之内这个下限出发,连续地向上变化,通过完全符合Poisson分布的基准状态,再向上演进到各点完全均匀分布于二维空间内的上限,这样一个连续系列将包括着二维空间分布模式的全部状况。这个推论的导出对于我们处理病例空间分布格局,带来了极为重要的启示。因此,有可能将真实环境中所存在的某病病例格局,纳入一个统一的,可以进行精确数量比较的空间分布谱之中。
, 百拇医药
在此假设下,受生态学研究成果的启示,针对不同的生境特点我们制定了四种聚集尺度:适用于大范围生境(全省、全市)的R尺度(R-Scale)、适用于小范围生境(县以下的特定生境及由一个或几个自然村组成的微小生境)的E-index谱分析、距离聚集指标I(d)分析法和考虑距离相关性的空间自相关与分布型指数(Iz)法。
3.4 基于Iwao -m生态学空间模型疾病空间动态模型[12~16]
-m生态学空间模型疾病空间动态模型[12~16]
在生态学研究中,Iwao在1968、1969年所描述的生物种群空间分布图式为: =α+βm,其中
=α+βm,其中 为种群平均拥挤度,m为平均密度,并且对α,β的生物学含义作出了明确的解释。在本研究中,我们根据这些生态学研究的基本思想,提出适合描述疾病空间动态的基本流行病学假设,并据此假设建立相应的数学模型,定量地刻划其空间分布动态。
为种群平均拥挤度,m为平均密度,并且对α,β的生物学含义作出了明确的解释。在本研究中,我们根据这些生态学研究的基本思想,提出适合描述疾病空间动态的基本流行病学假设,并据此假设建立相应的数学模型,定量地刻划其空间分布动态。
, 百拇医药
在某一特定生境内病例空间分布格局指标可以由病例平均密度mc(case density)及平均拥挤度 c(case cowding)来描述。定义如下:
c(case cowding)来描述。定义如下: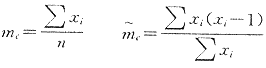
当样本含量较大时 c有近似形式
c有近似形式
 c的第一种形式反映对于每个个体,在同一样方中有多少其它个体的平均数,即每个个体在它样方中“邻居”的平均数,或者说是平均每个个体有多少在同单位内的其它个体,可以认为这些个体是与第一个个体共占一个单位。
c的第一种形式反映对于每个个体,在同一样方中有多少其它个体的平均数,即每个个体在它样方中“邻居”的平均数,或者说是平均每个个体有多少在同单位内的其它个体,可以认为这些个体是与第一个个体共占一个单位。 c的第二种形式则直观地反映了
c的第二种形式则直观地反映了 c与病例空间格局的关系,因为在随机格局中s2/
c与病例空间格局的关系,因为在随机格局中s2/ =1,故有
=1,故有 c=
c= 。于是有:
。于是有: c/
c/ =1,为随机格局;
=1,为随机格局; c/
c/ <1,为均匀格局;
<1,为均匀格局; c/
c/ >1,为聚集格局。
>1,为聚集格局。 c/
c/ 刻划了病例空间格局的内在性质,反映了其在一定条件下的聚集状态的变化。如果在时间维上,建立时间t与
刻划了病例空间格局的内在性质,反映了其在一定条件下的聚集状态的变化。如果在时间维上,建立时间t与 c/
c/ 间的函数关系,则能定量反映聚集动态的变化规律。
间的函数关系,则能定量反映聚集动态的变化规律。
, http://www.100md.com
这里我们的假设是病例的平均拥挤度 c与其平均密度mc间存在着某种线性或非线性关系,而这种线性或非线性关系则体现了病例的空间分布动态机制,进而反映其流行病学机制。在以上假设的基础上,根据
c与其平均密度mc间存在着某种线性或非线性关系,而这种线性或非线性关系则体现了病例的空间分布动态机制,进而反映其流行病学机制。在以上假设的基础上,根据 c和mc的含义以及疾病的流行病学特点,我们提出以下模型:
c和mc的含义以及疾病的流行病学特点,我们提出以下模型: c=α+β1mc+β2m2c+β3m3c+…+βkmkc
c=α+β1mc+β2m2c+β3m3c+…+βkmkc
, http://www.100md.com 一般情况下,取 c的3次模型便可以达到拟合精度:
c的3次模型便可以达到拟合精度: c=α+βmc+γm2c+δm3c
c=α+βmc+γm2c+δm3c
模型中参数的流行病学含义为:
①、α是每个基本成分中个体数分布的平均拥挤数,称为基本聚集度指标:
α=0时,分布的基本成分是单个个体,病例间没有相互内在联系,既不相互排斥也不相互吸引;
α>0时,分布的基本成分是个群体,病例间存在着某种内在联系,病例间相互吸引;
, 百拇医药
α<0时,病例间存在相互排斥的内在联系特点。
②、β表示基本成分的空间格局,体现了基本成分的相对聚集度,称为密度—聚集度指标:
β=0时,病例的空间格局为随机分布;
β<1时,病例的空间格局为均匀分布,β越小分布越均匀;
β>0时,病例的空间格局为聚集分布,β越大分布越聚集。
③、γ+2δm是基本成分的相对聚集度随病例平均密度而变化的速率。
④、2δ是基本成分的相对聚集度随病例平均密度变化的加速率。
⑤、当病例密度足够低时,模型中右端第四项m3为高阶无穷小,可以忽略,即相当于不考虑加速度,δ=0,这是模型为: c=α+βmc+γm2c
c=α+βmc+γm2c
, 百拇医药
⑥、当右端的m2也看成是无穷小时,则m2也可以忽略,即相当于不考虑速率,γ=0,这时模型为: c=α+βmc也就是Iwao的原模型。
c=α+βmc也就是Iwao的原模型。
⑦、若 c与mc的k次方间仍不呈线性,则可以对它实施变量变换,使其达到线性化的要求。例如对
c与mc的k次方间仍不呈线性,则可以对它实施变量变换,使其达到线性化的要求。例如对 c实施对数变换,则模型变为:
c实施对数变换,则模型变为:
ln( c)=α+β1m+β2m2+β3βm3+…+βkmk
c)=α+β1m+β2m2+β3βm3+…+βkmk
, 百拇医药
⑧、评价模型拟合优度的指标我们定义为偏离度(B,Bias):
其中, c为模型计算所得的平均拥挤度的估计值。
c为模型计算所得的平均拥挤度的估计值。
模型主要用于两方面:一是研究时间维的某一特定生境内某病病例的空间分布动态规律,即对于某一特定生境,计算其内不同时间病例分布的 c与mc,建立模型,以反映该特定生境内病例的空间分布随时间的变化规律;二是在某个由若干个亚生境组成的大的特定生境内,在同一时点上或时期内,计算各亚生境内的病例分布的
c与mc,建立模型,以反映该特定生境内病例的空间分布随时间的变化规律;二是在某个由若干个亚生境组成的大的特定生境内,在同一时点上或时期内,计算各亚生境内的病例分布的 c与mc,建立模型,以反映该特定生境内病例的空间分布随亚生境的变化规律;应用模型中的参数信息合理解释疾病的流行病学机制,提出相应的防治措施。
c与mc,建立模型,以反映该特定生境内病例的空间分布随亚生境的变化规律;应用模型中的参数信息合理解释疾病的流行病学机制,提出相应的防治措施。
, 百拇医药
参考文献
1 陈峰,杨树勤.疾病的复合分布模型研究.中国卫生统计,1995,6(12):12~15.
2 陈峰,杨树勤.论负二项分布的应用条件.中国卫生统计,1995,4(12):21~24.
3 陈峰,杨树勤.β-二项分布及其医学应用.中国卫生统计,1996,6(13):12~15.
4 陈峰,杨树勤.PP分布、PB分布及其应用.中国卫生统计,1996,4(13):6~8.
5 陈峰,杨树勤.带协变量的统计分布及其应用.中国卫生统计,1995,6(13):8~11.
6 陈峰,杨树勤.混合Poisson分布及其应用.中国卫生统计,1997,2(14).
, http://www.100md.com
7 马学尼,叶镇国.水文学.中国建筑出版社,1989,21~74.
8 沈佐锐等.用Pearson-Ⅲ型曲线拟合菜蚜种群空间分布的初步研究.生态学报,1985,4(5):363~370.
9 蔡晓明等.大白菜上七星瓢虫空间格局及抽样技术研究.生态学杂志,1991,10(5):6~11.
10 牛文元.生态系统的空间分布.生态学报,1984,4(4):299~308.
11 李天生,周国法.昆虫种群距离聚集度指标的研究.生态学报,1991,4(11):345~3487.
12 李天生,周国法.空间自相关与分布型指数研究.生态学报,1994,3(14):328~331.
13 Iwao, S. and Kuno,E:Use of the regression of mean corwding on mean density for estimating sample size and the transformation of data for the analysis of variance.Res. Popul.Ecol.1984,210~214.
, http://www.100md.com
14 Iwao,S. and Kuno,E:An approach to the analysis of aggregation patterns in biological popuations. Statistical Ecology. 1, 461~513, Penn. State Univ. Press. 1971.
15 Iwao, S: Application of the m-m method to the analysis of spatial pattern by changing the quadrat sine Res. Popul. Ecol. 1972,14(1):79~128.
16 Iwao, S: A new regression method for analysis the aggregation pattern of animal populations Res. Popul. Ecol 1968,10(1):1~20.
17 徐汝梅等.改正的Iwao m-m模型.生态学报,1984,2(4):111~118.
收稿日期:1998-09-08, http://www.100md.com
单位:山东医科大学公共卫生学院 济南250012
关键词:
数理医药学杂志990405
疾病的发生受多种因素的影响,由于时间不同、人群不同、地区不同,或其他条件的改变均可使疾病的流行规律发生变化。因此,必须以动态和变化的观点去认识疾病流行规律[1]。对疾病流行动态的研究包括三个方面:一是追踪流行强度随时间的变化,即所谓流行强度的时间动态问题;二是观察不同特征人群流行强度的变化,即所谓流行强度的人间动态问题;三是考察患病个体在空间散步状态的变化,即所谓空间动态问题。其中,对疾病空间动态的研究尤为重要,而目前又研究得不够深入。本研究从疾病生态学的观点出发,将生态学的基本原理和方法同流行病学、概率论与数理统计、系统论等相结合,提出了疾病空间分布动态模式的基本假设,在此假设下,以肾综合征出血热为研究对象,建立五大类表达疾病空间动态格局的一系列数学模型,这无论对丰富流行病学理论还是对制定切实可行的疾病防治措施都具有重要意义。本文是整个研究中的总论部分。
, 百拇医药
1 生态学的空间格局观点
按照生态学的观点,正确地表征生态系统的空间格局,并对其进行数量分析与比较,是判断区域生态平衡,追踪生态演变,评价生态系统干预措施效果的必要条件之一。任何生态系统类型,离开了它所处的空间格局,其它诸如环境与生物诸要素相互作用的问题,生态系统的发展与演变等问题,统统失去了讨论的基础。就某一特定的生态系统而言,尽管有较相似的非生物环境条件,该生态系统的空间格局仍会有明显的差异。至于对自然环境很不一致的地域,这种空间格局所表现出的差异就会更大。一般来说,空间结构上的差异,不仅影响生态系统的功能,最终将影响到该生态系统的总输出。从这个意义上讲,探求生态系统的空间结构规律,对于控制生态系统具有重要意义。对于疾病生态系统而言,同样存在着以上生态学的共性问题。因而,本研究将生态学的基本原理同概率论与数理统计相结合,根据疾病流行病学特点,提出以下流行病学假设,并以此假设建立疾病空间动态模型。
2 疾病空间格局类型及其动态的流行病学假设
, http://www.100md.com
疾病空间格局是指其在所处的特定生境空间中的结构,这种结构的形式是疾病对环境条件的适应或选择的结果。这里设想疾病的空间格局存在三种类型:
①随机格局 疾病病例个体之间相互独立,既无吸引也无排斥,病例间没有一定的流行病学联系。描述这种空间格局的概率模型是Poisson分布,其主要特征是s2=
 ,其中
,其中 是疾病病例的密度,即平均每个样本单位(样方)中的病例数,s2是相应样本的方差。
是疾病病例的密度,即平均每个样本单位(样方)中的病例数,s2是相应样本的方差。②聚集格局 疾病病例个体间存在某种联系,在空间内出现聚块(patch)。描述这种空间格局的概率模型主要是集中邻接分布。如Γ-Poisson分布(负二项分布)、Poisson-Poisson分布(Neymans A型分布)、β-二项分布、Poisson-二项分布、带协变量的分布(如时依Poisson)、混合Poisson分布等,它们的共同特点是s2>
 。
。, http://www.100md.com
③均匀格局 假定在一特定生境中某病病例个体之间是相互排斥的,这种空间格局常用二项分布来描述。其特点是s2<
 。
。我们认为疾病的发生受诸多因素的影响,这些因素在不断地发生变化,因而病例无论取那种空间格局,都不是一成不变的。①、②、③三种格局之间乃至描述它们的概率分布之间并不是独立无关的。无论从疾病生态学或流行病学意义上还是从概率论与数理统计学意义上,病例的所有可能分布型组成了一个连续统(这是一个生态学术语,在此借用),其一端是均匀分布,另一端是高度聚集的分布,而Piosson分布则是这个连续统中间的一个过渡点。从时间上考虑,随着病例在一特定生境内的密度变化,其空间格局也不断变化着,于是就可能经历由Piosson分布经负二项分布或其他复合分布到某种高度偏态,拖尾很长的高聚集分布的动态过程。这些假设思想是符合疾病的实际发生与流行动态的,因而在此前提下,以流行病学和概率论与数理统计的理论为指导,应用生态学、系统论等领域研究的最新成果,对疾病空间动态进行系统研究,建立揭示其发生与流行的空间动态的各种数学模型,便可能会找到疾病发生与流行的本质规律。
, 百拇医药
3 空间动态模型建模方法
根据以上假设,本研究以山东省、山东省临沂市、临沂市所辖的平邑县的肾综合征出血热(HRFS)为研究对象,建立了一系列疾病空间分布动态的模型,现简介如下:
3.1 离散性频率模型
这类模型为离散性的空间动态模型,是在时间维上,用各种概率分布模型模拟病例的空间分布动态,从而揭示其流行规律。除用二项分布、Poisson分布等单一模型外,主要应用陈锋、杨树勤介绍的各种复合模型[1~6]。
3.2 Pearson-Ⅲ连续性空间分布模型[7,8]
由于疾病的发生是病因、宿主、环境三者共同作用的结果,所以其变化会很复杂。这里假设某病病例的空间分布特点是在时间维上变化较快,在一定时间时期可达到相当大的数量,一定范围内个体数变量的离散程度较高。在这种情况下,用前面介绍的离散型频率模型,就不合适,这是由于它们的变通性小,每种模型只是适用于特定的分布,参数信息少,分布的直观性差。为克服离散型频率模型的这些缺点,本研究将Pearson-Ⅲ连续性空间分布模型引入疾病空间动态研究获得满意效果。其基本方法是:对于某一特定生境,在时间维上(月份、季度、流行年),采用回顾性或前瞻性方法,连续观察若干次(n次)内某病病例的空间分布情况,或在同一时期内,同时观察若干个(n个)特定生境内某病病例的空间分布情况,各样本量由于取样时间或地点的约束和个体分布密度的不同而不相等。这些变量组成的样本可视为来自n个概率分布总体,把它们串起来可望得到对特定生境内某病病例概率分布的动态特点。
, http://www.100md.com
Pearson-Ⅲ连续性空间分布模型的概率函数为:

其中,α>0,β>0,x≥b,Pearson-Ⅲ连续性空间分布是一个三参数分布。其参数估计方法有矩法、适线法、极大似然法和单纯性法等。其空间分布判定指标及其流行病学含义为:
①

Q<1,聚集分布,Q越小聚集性越大;
Q=1,随机分布;
Q>1,均匀分布,Q越大分布越均匀。
②
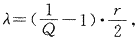 其中r=x20.5(2αQ2/(1-Q)β2
其中r=x20.5(2αQ2/(1-Q)β2, 百拇医药
λ>2时,聚集由病例间存在着内在联系所引起,这种内在联系很可能反映了致病因子及环境因子的聚集性;
λ<2时,聚集由病例所处的地理环境决定,包括引起HRFS病例发生的若干环境因素的集合。
3.3 基于Taylor幂法则[9~12]的各种聚集尺度模型
我们假定某病病例在某一特定生境中的空间分布遵循下面一条概念性的空间分布规律:在某一特定生境内,病例的空间分布,总是以Poisson分布为基准,沿着两个相反的方向演化。其一,与Poisson分布相比,在二维空间内点的分布具有更为聚合,更加集族(灶性发病点)的趋势;其二,与Poisson分布相比在二维空间内点的分布具有更为分散、更加均匀的趋势(病例高度散发)。作为上述两种趋势的极端表现,前者所有的点均重叠地分布于一个唯一的面积单元(即样本单位)之中,可以看作几个相集在一起的高度聚合的特殊分布;而后者则是所有的点在一个二维空间内各占据相等的面积,即点均匀地排布于每一面积单元之中,它可以看作为各点距离之间完全相等的高度分散的特殊分布。由上述可以推论出,在点的空间分布的基本表述上,可以发现这些点的空间分布模式能够从完全聚合于一个唯一的面积单元之内这个下限出发,连续地向上变化,通过完全符合Poisson分布的基准状态,再向上演进到各点完全均匀分布于二维空间内的上限,这样一个连续系列将包括着二维空间分布模式的全部状况。这个推论的导出对于我们处理病例空间分布格局,带来了极为重要的启示。因此,有可能将真实环境中所存在的某病病例格局,纳入一个统一的,可以进行精确数量比较的空间分布谱之中。
, 百拇医药
在此假设下,受生态学研究成果的启示,针对不同的生境特点我们制定了四种聚集尺度:适用于大范围生境(全省、全市)的R尺度(R-Scale)、适用于小范围生境(县以下的特定生境及由一个或几个自然村组成的微小生境)的E-index谱分析、距离聚集指标I(d)分析法和考虑距离相关性的空间自相关与分布型指数(Iz)法。
3.4 基于Iwao
 -m生态学空间模型疾病空间动态模型[12~16]
-m生态学空间模型疾病空间动态模型[12~16]在生态学研究中,Iwao在1968、1969年所描述的生物种群空间分布图式为:
 =α+βm,其中
=α+βm,其中 为种群平均拥挤度,m为平均密度,并且对α,β的生物学含义作出了明确的解释。在本研究中,我们根据这些生态学研究的基本思想,提出适合描述疾病空间动态的基本流行病学假设,并据此假设建立相应的数学模型,定量地刻划其空间分布动态。
为种群平均拥挤度,m为平均密度,并且对α,β的生物学含义作出了明确的解释。在本研究中,我们根据这些生态学研究的基本思想,提出适合描述疾病空间动态的基本流行病学假设,并据此假设建立相应的数学模型,定量地刻划其空间分布动态。, 百拇医药
在某一特定生境内病例空间分布格局指标可以由病例平均密度mc(case density)及平均拥挤度
 c(case cowding)来描述。定义如下:
c(case cowding)来描述。定义如下: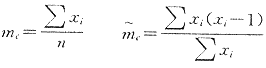
当样本含量较大时
 c有近似形式
c有近似形式
 c的第一种形式反映对于每个个体,在同一样方中有多少其它个体的平均数,即每个个体在它样方中“邻居”的平均数,或者说是平均每个个体有多少在同单位内的其它个体,可以认为这些个体是与第一个个体共占一个单位。
c的第一种形式反映对于每个个体,在同一样方中有多少其它个体的平均数,即每个个体在它样方中“邻居”的平均数,或者说是平均每个个体有多少在同单位内的其它个体,可以认为这些个体是与第一个个体共占一个单位。 c的第二种形式则直观地反映了
c的第二种形式则直观地反映了 c与病例空间格局的关系,因为在随机格局中s2/
c与病例空间格局的关系,因为在随机格局中s2/ =1,故有
=1,故有 c=
c= 。于是有:
。于是有: c/
c/ =1,为随机格局;
=1,为随机格局; c/
c/ <1,为均匀格局;
<1,为均匀格局; c/
c/ >1,为聚集格局。
>1,为聚集格局。 c/
c/ 刻划了病例空间格局的内在性质,反映了其在一定条件下的聚集状态的变化。如果在时间维上,建立时间t与
刻划了病例空间格局的内在性质,反映了其在一定条件下的聚集状态的变化。如果在时间维上,建立时间t与 c/
c/ 间的函数关系,则能定量反映聚集动态的变化规律。
间的函数关系,则能定量反映聚集动态的变化规律。, http://www.100md.com
这里我们的假设是病例的平均拥挤度
 c与其平均密度mc间存在着某种线性或非线性关系,而这种线性或非线性关系则体现了病例的空间分布动态机制,进而反映其流行病学机制。在以上假设的基础上,根据
c与其平均密度mc间存在着某种线性或非线性关系,而这种线性或非线性关系则体现了病例的空间分布动态机制,进而反映其流行病学机制。在以上假设的基础上,根据 c和mc的含义以及疾病的流行病学特点,我们提出以下模型:
c和mc的含义以及疾病的流行病学特点,我们提出以下模型: c=α+β1mc+β2m2c+β3m3c+…+βkmkc
c=α+β1mc+β2m2c+β3m3c+…+βkmkc, http://www.100md.com 一般情况下,取
 c的3次模型便可以达到拟合精度:
c的3次模型便可以达到拟合精度: c=α+βmc+γm2c+δm3c
c=α+βmc+γm2c+δm3c模型中参数的流行病学含义为:
①、α是每个基本成分中个体数分布的平均拥挤数,称为基本聚集度指标:
α=0时,分布的基本成分是单个个体,病例间没有相互内在联系,既不相互排斥也不相互吸引;
α>0时,分布的基本成分是个群体,病例间存在着某种内在联系,病例间相互吸引;
, 百拇医药
α<0时,病例间存在相互排斥的内在联系特点。
②、β表示基本成分的空间格局,体现了基本成分的相对聚集度,称为密度—聚集度指标:
β=0时,病例的空间格局为随机分布;
β<1时,病例的空间格局为均匀分布,β越小分布越均匀;
β>0时,病例的空间格局为聚集分布,β越大分布越聚集。
③、γ+2δm是基本成分的相对聚集度随病例平均密度而变化的速率。
④、2δ是基本成分的相对聚集度随病例平均密度变化的加速率。
⑤、当病例密度足够低时,模型中右端第四项m3为高阶无穷小,可以忽略,即相当于不考虑加速度,δ=0,这是模型为:
 c=α+βmc+γm2c
c=α+βmc+γm2c, 百拇医药
⑥、当右端的m2也看成是无穷小时,则m2也可以忽略,即相当于不考虑速率,γ=0,这时模型为:
 c=α+βmc也就是Iwao的原模型。
c=α+βmc也就是Iwao的原模型。⑦、若
 c与mc的k次方间仍不呈线性,则可以对它实施变量变换,使其达到线性化的要求。例如对
c与mc的k次方间仍不呈线性,则可以对它实施变量变换,使其达到线性化的要求。例如对 c实施对数变换,则模型变为:
c实施对数变换,则模型变为:ln(
 c)=α+β1m+β2m2+β3βm3+…+βkmk
c)=α+β1m+β2m2+β3βm3+…+βkmk, 百拇医药
⑧、评价模型拟合优度的指标我们定义为偏离度(B,Bias):

其中,
 c为模型计算所得的平均拥挤度的估计值。
c为模型计算所得的平均拥挤度的估计值。模型主要用于两方面:一是研究时间维的某一特定生境内某病病例的空间分布动态规律,即对于某一特定生境,计算其内不同时间病例分布的
 c与mc,建立模型,以反映该特定生境内病例的空间分布随时间的变化规律;二是在某个由若干个亚生境组成的大的特定生境内,在同一时点上或时期内,计算各亚生境内的病例分布的
c与mc,建立模型,以反映该特定生境内病例的空间分布随时间的变化规律;二是在某个由若干个亚生境组成的大的特定生境内,在同一时点上或时期内,计算各亚生境内的病例分布的 c与mc,建立模型,以反映该特定生境内病例的空间分布随亚生境的变化规律;应用模型中的参数信息合理解释疾病的流行病学机制,提出相应的防治措施。
c与mc,建立模型,以反映该特定生境内病例的空间分布随亚生境的变化规律;应用模型中的参数信息合理解释疾病的流行病学机制,提出相应的防治措施。, 百拇医药
参考文献
1 陈峰,杨树勤.疾病的复合分布模型研究.中国卫生统计,1995,6(12):12~15.
2 陈峰,杨树勤.论负二项分布的应用条件.中国卫生统计,1995,4(12):21~24.
3 陈峰,杨树勤.β-二项分布及其医学应用.中国卫生统计,1996,6(13):12~15.
4 陈峰,杨树勤.PP分布、PB分布及其应用.中国卫生统计,1996,4(13):6~8.
5 陈峰,杨树勤.带协变量的统计分布及其应用.中国卫生统计,1995,6(13):8~11.
6 陈峰,杨树勤.混合Poisson分布及其应用.中国卫生统计,1997,2(14).
, http://www.100md.com
7 马学尼,叶镇国.水文学.中国建筑出版社,1989,21~74.
8 沈佐锐等.用Pearson-Ⅲ型曲线拟合菜蚜种群空间分布的初步研究.生态学报,1985,4(5):363~370.
9 蔡晓明等.大白菜上七星瓢虫空间格局及抽样技术研究.生态学杂志,1991,10(5):6~11.
10 牛文元.生态系统的空间分布.生态学报,1984,4(4):299~308.
11 李天生,周国法.昆虫种群距离聚集度指标的研究.生态学报,1991,4(11):345~3487.
12 李天生,周国法.空间自相关与分布型指数研究.生态学报,1994,3(14):328~331.
13 Iwao, S. and Kuno,E:Use of the regression of mean corwding on mean density for estimating sample size and the transformation of data for the analysis of variance.Res. Popul.Ecol.1984,210~214.
, http://www.100md.com
14 Iwao,S. and Kuno,E:An approach to the analysis of aggregation patterns in biological popuations. Statistical Ecology. 1, 461~513, Penn. State Univ. Press. 1971.
15 Iwao, S: Application of the m-m method to the analysis of spatial pattern by changing the quadrat sine Res. Popul. Ecol. 1972,14(1):79~128.
16 Iwao, S: A new regression method for analysis the aggregation pattern of animal populations Res. Popul. Ecol 1968,10(1):1~20.
17 徐汝梅等.改正的Iwao m-m模型.生态学报,1984,2(4):111~118.
收稿日期:1998-09-08, http://www.100md.com