非竞争性抑制系统中的膜动载动力学方程
作者:李 泉
单位:徐州医学院 徐州221002
关键词:易化运输;膜运载动力学;非竞争性抑制系统
数理医药学杂志990401
摘 要 在易化运输机制下,若抑制剂I的加入并不扰乱载体T和ST之间的平衡,即I可结合到T和ST上,S也可以结合到T和ST上,则S和I不互相排斥。导出了这种非竞争性抑制系统中的膜运载动力学方程。
在易化运输机制下,根据膜运载动力学的基本方程[1],细胞膜上的活动性部分载体先与细胞膜外被选择吸收的底物相结合,然后通过细胞膜把底物分子释放到细胞内部去。在这个过程中,载体分子被底物分子饱和时会产生同酶动力学中的那种饱和现象[2]。除了在文献[1]中导出了与酶动力学中的Michaelis-Menten方程相类似的膜运载动力学相类似的膜运载动力学的基本方程外,还导出了与酶—底物的竞争性抑制系统相类似的竞争性抑制系统中的膜运载动力学方程[3],该系统已有国外学者的工作早已证明其存在[4]。本文将导出与酶—底物的非竞争性抑制系统相类似的非竞争性抑制系统中的膜运载动力学方程。
, 百拇医药
我们考察了载体T同时与底物S和抑制剂I的反应。若抑制剂I加入后,I与载体T的结合并不影响底物S与载体T的结合能力,即I可结合到T和ST上,S也可以结合到I和IT上,S和I不是互相排斥的,我们称之为非竞争性抑制。其反应式可表述为:

这里,我们假定SIT不能分解成生成物。又由于底物S和抑制剂互不排斥,因此,I与T、I与ST结合的速度常数相等,S与T、S与IT结合的速度常数相等。同样,IT、SIT分解出I的速度常数相等,ST、SIT分解出S的速度常数相等。
与上面的反应式相应的动力学方程为: (1)
(1) (2)
(2)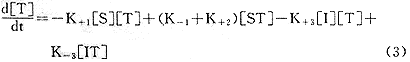


 (6)
(6) (7)
(7)
, http://www.100md.com
将式(3)~(6)相加
故
[T]+[ST]+[IT]+[SIT]=[T]0 (const) (8)
由平衡态假设,有
K+1[S][T]=K-1[ST]
K+1[IT][S]=K-1[SIT]
K+3[I][T]=K-3[IT]
K+3[ST][I]=K-3[SIT]
, http://www.100md.com
于是 (9)
(9) (10)
(10)
由(7)式,有
V=K+2[ST]
利用(8)式,有 (11)
(11)
由(9),(10)两式得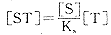
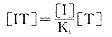

, http://www.100md.com
代入(11)式,并记K+2[T]0=Vmax,整理可得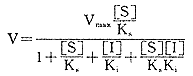
或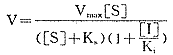 (12)
(12)
此即易化运输机制下,非竞争性抑制系统中的膜运载动力学方程。其V-[S]曲线如图1所示。
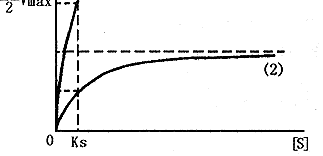
图1
方程(12)的双倒数式为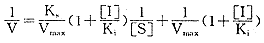 (13)
(13)
, http://www.100md.com
其L—B图为直线(见图2)。Ks不会被抑制剂I所改变,而且不同抑制剂浓度的L—B图是从相同横截距向外呈扇形展开的一组直线,抑制剂的加入使直线变陡,Vmax减少。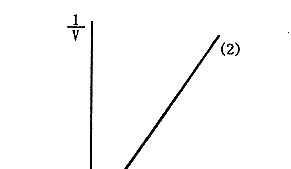
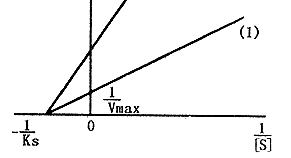
图2
如果在不同基质浓度的研究摄取率的实验中得到如图1形状的曲线或如图2形状的直线,就可以认为该系统属于非竞争性抑制系统。
参考文献
1 李泉.易化运输机制下膜运载动力学的基本方程.数理医药学杂志,1995,8(1).
2 周怀梧.医用生物数学.人民卫生出版社,1990.
3 李泉.竞争性抑制系统中的膜运载动力学方程.数理医药学杂志,1997,10(4).
4 Arme C. and Read C.P. (1968) Studies on membrane transport Ⅱ.The absorption of acetate and butyrate by Hymenolepis diminuta (Cestoda). Biol Bull 135,80~90.
收稿日期:1999-01-06, http://www.100md.com
单位:徐州医学院 徐州221002
关键词:易化运输;膜运载动力学;非竞争性抑制系统
数理医药学杂志990401
摘 要 在易化运输机制下,若抑制剂I的加入并不扰乱载体T和ST之间的平衡,即I可结合到T和ST上,S也可以结合到T和ST上,则S和I不互相排斥。导出了这种非竞争性抑制系统中的膜运载动力学方程。
在易化运输机制下,根据膜运载动力学的基本方程[1],细胞膜上的活动性部分载体先与细胞膜外被选择吸收的底物相结合,然后通过细胞膜把底物分子释放到细胞内部去。在这个过程中,载体分子被底物分子饱和时会产生同酶动力学中的那种饱和现象[2]。除了在文献[1]中导出了与酶动力学中的Michaelis-Menten方程相类似的膜运载动力学相类似的膜运载动力学的基本方程外,还导出了与酶—底物的竞争性抑制系统相类似的竞争性抑制系统中的膜运载动力学方程[3],该系统已有国外学者的工作早已证明其存在[4]。本文将导出与酶—底物的非竞争性抑制系统相类似的非竞争性抑制系统中的膜运载动力学方程。
, 百拇医药
我们考察了载体T同时与底物S和抑制剂I的反应。若抑制剂I加入后,I与载体T的结合并不影响底物S与载体T的结合能力,即I可结合到T和ST上,S也可以结合到I和IT上,S和I不是互相排斥的,我们称之为非竞争性抑制。其反应式可表述为:


这里,我们假定SIT不能分解成生成物。又由于底物S和抑制剂互不排斥,因此,I与T、I与ST结合的速度常数相等,S与T、S与IT结合的速度常数相等。同样,IT、SIT分解出I的速度常数相等,ST、SIT分解出S的速度常数相等。
与上面的反应式相应的动力学方程为:
 (1)
(1) (2)
(2)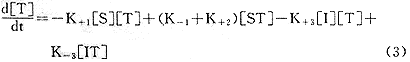


 (6)
(6) (7)
(7), http://www.100md.com
将式(3)~(6)相加

故
[T]+[ST]+[IT]+[SIT]=[T]0 (const) (8)
由平衡态假设,有
K+1[S][T]=K-1[ST]
K+1[IT][S]=K-1[SIT]
K+3[I][T]=K-3[IT]
K+3[ST][I]=K-3[SIT]
, http://www.100md.com
于是
 (9)
(9) (10)
(10)由(7)式,有
V=K+2[ST]
利用(8)式,有
 (11)
(11)由(9),(10)两式得
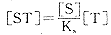
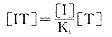

, http://www.100md.com
代入(11)式,并记K+2[T]0=Vmax,整理可得
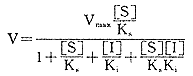
或
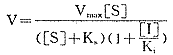 (12)
(12)此即易化运输机制下,非竞争性抑制系统中的膜运载动力学方程。其V-[S]曲线如图1所示。


图1
方程(12)的双倒数式为
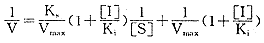 (13)
(13), http://www.100md.com
其L—B图为直线(见图2)。Ks不会被抑制剂I所改变,而且不同抑制剂浓度的L—B图是从相同横截距向外呈扇形展开的一组直线,抑制剂的加入使直线变陡,Vmax减少。

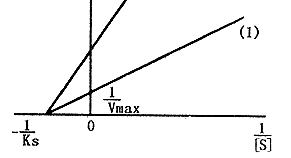
图2
如果在不同基质浓度的研究摄取率的实验中得到如图1形状的曲线或如图2形状的直线,就可以认为该系统属于非竞争性抑制系统。
参考文献
1 李泉.易化运输机制下膜运载动力学的基本方程.数理医药学杂志,1995,8(1).
2 周怀梧.医用生物数学.人民卫生出版社,1990.
3 李泉.竞争性抑制系统中的膜运载动力学方程.数理医药学杂志,1997,10(4).
4 Arme C. and Read C.P. (1968) Studies on membrane transport Ⅱ.The absorption of acetate and butyrate by Hymenolepis diminuta (Cestoda). Biol Bull 135,80~90.
收稿日期:1999-01-06, http://www.100md.com