狂犬病发病季节性特征的数理分析
作者:朱玉贵 张泽云
单位:湖北省长阳土家族自治县卫生防疫站 长阳443500
关键词:狂犬病季节性;圆形分布法;余弦模型
数理医药学杂志990424
摘 要 根据湘、鄂、豫三省狂犬病季节分布资料,应用圆形分布法分析表明该区域狂犬病具有明显的季节性高峰特征。
人们对狂犬病的人群分布和地区分布的描述性研究较多,但对其季节性分布特征的研究尚未见报道。本文应用圆形分布法与余弦模型对湖南、湖北和河南三省12090例狂犬病的分月资料进行分析,以探索其发病的季节性特征。
1 资料与方法
1.1 资料来源
, 百拇医药
湖南省1981~1996年狂犬病死亡月分布资料来源于文献[1],由于狂犬病病死率100%,病程一般不超过6天[2],按发病统计对结果影响不大,故以下称发病资料(以 -4°、φ-4°估计发病高峰时点)。湖北省1987~1993年分月发病资料来源于《湖北省疫情资料汇编》。河南省1951~1996年狂犬病发病时间分布来源于文献[3],见表1。
-4°、φ-4°估计发病高峰时点)。湖北省1987~1993年分月发病资料来源于《湖北省疫情资料汇编》。河南省1951~1996年狂犬病发病时间分布来源于文献[3],见表1。
表1 湘、鄂、豫三省狂犬病月发病构成分布
年份
月 构 成 比(%)
1
2
3
, 百拇医药
4
5
6
7
8
9
10
11
12
合计
湖北省
1987
3.36
3.62
, 百拇医药
5.43
7.24
8.79
9.04
8.27
12.40
11.63
10.08
9.30
10.84
100.00
1988
6.04
, 百拇医药
3.38
8.94
4.83
7.02
11.35
12.56
10.14
11.11
10.63
7.00
7.00
100.00
1989
, http://www.100md.com
6.78
2.01
7.29
6.28
9.04
7.54
9.30
9.55
10.55
11.56
10.05
10.05
100.00
, http://www.100md.com
1990
8.04
7.07
5.16
6.75
7.40
10.29
11.25
11.25
11.25
9.32
8.04
4.18
, http://www.100md.com
100.00
1991
8.80
4.80
7.20
6.80
8.80
8.80
10.00
13.20
10.80
6.80
9.20
, 百拇医药
4.80
100.00
1992
8.78
6.76
6.08
8.78
10.14
10.81
13.51
4.73
8.11
8.11
, 百拇医药
9.46
4.73
100.00
1993
9.38
7.81
6.25
7.81
10.94
12.50
9.37
9.37
17.19
, http://www.100md.com
4.69
1.56
3.14
100.00
1987~93
6.64
4.31
6.79
6.54
8.42
9.64
10.50
10.60
, http://www.100md.com
11.05
9.64
8.52
7.35
100.00
湖南省
1981~96
5.76
5.45
7.29
7.34
7.57
9.10
, 百拇医药
10.01
11.46
10.88
10.18
8.60
6.36
100.00
河南省
1951~96
4.70
4.54
5.44
6.35
, 百拇医药
7.38
8.85
11.45
12.52
10.70
10.33
9.42
8.32
100.00
合 计
5.63
5.02
6.72
, 百拇医药
6.95
7.66
9.12
10.47
11.60
10.86
10.13
8.80
7.04
100.00
1.2 分析方法
应用圆形分布法[4]计算各月发病频数,求平均角 =180°+arctg(Y/X),当本组X<0时;根据余弦模型和估计参数方法[5],由月发病数计算月构成比并转换成对数后建模,并据
=180°+arctg(Y/X),当本组X<0时;根据余弦模型和估计参数方法[5],由月发病数计算月构成比并转换成对数后建模,并据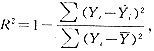 ,计算决定系数。2 结果与分析
,计算决定系数。2 结果与分析
, 百拇医药
2.1 该区域狂犬病的季节性高峰特征明显
经圆形分布法分年度分析湖北省7年资料,1987~1991年季节性高峰特征极显著(r>r0.01(n),P<0.01),发病高峰时点比较一致,在8月9日至9月16日,表明将各年度资料合并计算具有代表意义。进而对各省和三省合并资料进行分析,集中趋势值r均大于0.001,P<0.001,见表2。
表2 不同时、空狂犬病的圆形分布法分析结果
年份
r
P
平均角 (度)
(度)
, http://www.100md.com
发病高
峰日
湖北省
1987
0.1962
<0.001
240.34
9月1日
1988
0.1939
<0.001
222.29
8月13日
, http://www.100md.com
1989
0.1616
<0.001
255.27
9月16日
1990
0.1662
<0.001
221.64
8月13日
1991
0.1468
<0.01
, 百拇医药
217.70
8月9日
1987~93
0.1603
<0.001
228.60
8月20日
湖南省
1981~96
0.1428
<0.001
218.84
, 百拇医药 8月10日
河南省
1951~95
0.2107
<0.001
236.67
8月28日
合 计
0.1654
<0.001
230.20
8月21日
2.2 该区域狂犬病的发病高峰呈周期性、季节性分布符合余弦曲线模型
, 百拇医药
应用余弦模型分别对三省及其合并的月构成比进行对数拟合,据函数分程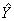 i=M+Acos(ωti-φ)分别建立简单余弦函数分程:
i=M+Acos(ωti-φ)分别建立简单余弦函数分程: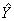 i(湘)=0.909+0.146cos(ti-204.88°) R2=0.9055
i(湘)=0.909+0.146cos(ti-204.88°) R2=0.9055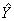 i(鄂)=0.907+0.149cos(ti-213.50°) R2=0.9064
i(鄂)=0.907+0.149cos(ti-213.50°) R2=0.9064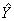 i(豫)=0.898+0.195cos(ti-220.77°) R2=0.9162
i(豫)=0.898+0.195cos(ti-220.77°) R2=0.9162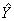 i(计)=0.906+0.153cos(ti-214.69°) R2=0.9595
i(计)=0.906+0.153cos(ti-214.69°) R2=0.9595
, http://www.100md.com
决定系数R2在0.9055~0.9595之间,表明简单余弦模型拟合效果已经甚佳,不必再建三角多项式。据φ=210°相当于8月15日和模型中的φ值,说明发病高峰在8月中、下旬。因余弦曲线上下波动呈对称性,故φ-180°所对应的2月中、下旬为发病低谷。代入ti值后取反对数得各月构成比理论值,见表3。表3 湘、鄂、豫三省狂犬病月发病构成比简单余弦模型拟合的理论值 月份
i
t
湖 南
湖 北
河 南
合 计
Yi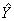 i
i
, http://www.100md.com
Yi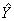 i
i
Yi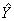 i
i
Yi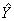 i
i
1
0
5.76
6.04
6.64
, http://www.100md.com
6.06
4.70
5.63
5.63
6.03
2
30
5.45
5.79
4.31
5.73
4.54
5.09
, 百拇医药
5.02
5.67
3
60
7.29
6.08
6.79
5.94
5.44
5.17
6.72
5.86
4
, http://www.100md.com
90
7.34
6.89
6.54
6.68
6.35
5.90
6.95
6.59
5
120
7.57
8.16
, http://www.100md.com
8.42
7.91
7.38
7.27
7.66
7.83
6
150
9.10
9.65
9.64
9.41
8.85
, http://www.100md.com
9.17
9.12
9.36
7
180
10.01
10.89
10.50
10.74
11.45
11.11
10.47
10.76
, http://www.100md.com
8
210
11.46
11.35
10.60
11.37
12.52
12.29
11.60
11.44
9
240
10.88
, 百拇医药
10.81
11.05
10.97
10.70
12.08
10.86
11.07
10
270
10.18
9.64
9.64
9.76
, 百拇医药
10.33
10.60
10.13
9.84
11
300
8.60
8.06
8.52
8.24
9.42
8.60
8.80
, http://www.100md.com
8.29
12
330
6.36
6.82
7.35
6.93
8.32
6.82
7.04
6.93
2.3 不同地区发病高峰时点的比较
湘、鄂、豫三省紧密相连,基本在同一东经跨度不同北纬范围。圆形分布法分析和余弦模型拟合转换的发病高峰时点一致,分别为8月10日、8月20日和8月28日,表明三省的发病高峰的点比较一致。同时可见,在同一经度范围发病高峰的点由南到北逐渐推后8~10天。
, http://www.100md.com
2.4 狂犬病的季节性与流行强度有一定关系
将湖北省发病率较高前三年、发病率较低的后两年合并分析,以雷氏Z值[6]检验平均角。后两年的结果说明,虽然分年度分析散发年的高峰特征不显著,但合并分析同样显示出季节性高峰特征。同时可见,反映季节性强弱的雷氏Z值与发病率呈正相关(r=0.9526,P<0.01),发病高峰时点随发病率下降呈前移趋势,见表4。表4 不同发病率的雷氏Z值与发病高峰时点 年份
发病率
(/10万)
平均角
(度)
雷氏Z值
, http://www.100md.com
P
发病高
峰日
1987~89
0.78
241.42
12.78
<0.001
9月2日
1990
0.59
221.64
8.59
, 百拇医药
<0.001
8月13日
1991
0.46
217.70
5.35
<0.01
8月9日
1992~93
0.19
180.23
3.74
<0.05
, 百拇医药
7月2日
3 讨论
圆形分布法分析疾病季节性的重要特点是能用平均角的检验判断疾病的季节性,余弦模型则能反映和预测疾病在全年各月的分布。本文通过一定区域较大样本的不同时、空的分析,证明狂犬病具有明显的季节性高峰特征,其分布符合余弦典线模型。圆形分布法与周期性回归分析,一致表明该区域狂犬病的发病高峰在8月中、下旬、发病低谷在2月中、下旬。
湘、鄂、豫三省狂犬病的发病高峰时点和由南到北的先后差距,反映高峰期前的气温是主要影响因素;分年段分析反映季节性与流行强度有关,提示在一些发病率低的地区,可能季节性高峰特征表现不明显。
将狂犬病的季节性分布建立成数学模型、发病高峰与低谷计算到月、日,还仅仅是尝试。与狂犬病无明显的季节性高峰、与春、夏、秋较多、冬季较少的持续高峰[2,7]等结论均有分歧。所以,关于狂犬病的季节性问题,还需要进一步研究论证。本文未进行样本角均数间的显著性检验,是因为受到圆形分布法中F检验的条件限制。
, http://www.100md.com
参考文献
1 郭绶衡,刘文,李树民,等.湖北省1951~1996年人间狂犬病流行病学分析.中国人兽共患病杂志,1998,14(1):78~78.
2 林放涛,于恩庶主编.狂犬病学.福建:福建科学技术出版社,1992,120~133.
3 张彦平,李林村,芮春军,等.河南省狂犬病流行病学分析.中国人兽共患病杂志,1998,14(3):74~76.
4 郭祖超主编.医用数理统计方法.北京:人民卫生出版社,1988,132~139.
5 胡克震,姜芝莉.周期性回归.中华预防医学杂志,1988,22(1):22~25.
6 金丕焕主编.医用统计方法.上海:上海医科大学出版社,1993,210~211.
7 夏祝辉主编.流行病学及传染病管理.北京:人民卫生出版社,1990,290.
收稿日期:1999-04-11, 百拇医药
单位:湖北省长阳土家族自治县卫生防疫站 长阳443500
关键词:狂犬病季节性;圆形分布法;余弦模型
数理医药学杂志990424
摘 要 根据湘、鄂、豫三省狂犬病季节分布资料,应用圆形分布法分析表明该区域狂犬病具有明显的季节性高峰特征。
人们对狂犬病的人群分布和地区分布的描述性研究较多,但对其季节性分布特征的研究尚未见报道。本文应用圆形分布法与余弦模型对湖南、湖北和河南三省12090例狂犬病的分月资料进行分析,以探索其发病的季节性特征。
1 资料与方法
1.1 资料来源
, 百拇医药
湖南省1981~1996年狂犬病死亡月分布资料来源于文献[1],由于狂犬病病死率100%,病程一般不超过6天[2],按发病统计对结果影响不大,故以下称发病资料(以
 -4°、φ-4°估计发病高峰时点)。湖北省1987~1993年分月发病资料来源于《湖北省疫情资料汇编》。河南省1951~1996年狂犬病发病时间分布来源于文献[3],见表1。
-4°、φ-4°估计发病高峰时点)。湖北省1987~1993年分月发病资料来源于《湖北省疫情资料汇编》。河南省1951~1996年狂犬病发病时间分布来源于文献[3],见表1。表1 湘、鄂、豫三省狂犬病月发病构成分布
年份
月 构 成 比(%)
1
2
3
, 百拇医药
4
5
6
7
8
9
10
11
12
合计
湖北省
1987
3.36
3.62
, 百拇医药
5.43
7.24
8.79
9.04
8.27
12.40
11.63
10.08
9.30
10.84
100.00
1988
6.04
, 百拇医药
3.38
8.94
4.83
7.02
11.35
12.56
10.14
11.11
10.63
7.00
7.00
100.00
1989
, http://www.100md.com
6.78
2.01
7.29
6.28
9.04
7.54
9.30
9.55
10.55
11.56
10.05
10.05
100.00
, http://www.100md.com
1990
8.04
7.07
5.16
6.75
7.40
10.29
11.25
11.25
11.25
9.32
8.04
4.18
, http://www.100md.com
100.00
1991
8.80
4.80
7.20
6.80
8.80
8.80
10.00
13.20
10.80
6.80
9.20
, 百拇医药
4.80
100.00
1992
8.78
6.76
6.08
8.78
10.14
10.81
13.51
4.73
8.11
8.11
, 百拇医药
9.46
4.73
100.00
1993
9.38
7.81
6.25
7.81
10.94
12.50
9.37
9.37
17.19
, http://www.100md.com
4.69
1.56
3.14
100.00
1987~93
6.64
4.31
6.79
6.54
8.42
9.64
10.50
10.60
, http://www.100md.com
11.05
9.64
8.52
7.35
100.00
湖南省
1981~96
5.76
5.45
7.29
7.34
7.57
9.10
, 百拇医药
10.01
11.46
10.88
10.18
8.60
6.36
100.00
河南省
1951~96
4.70
4.54
5.44
6.35
, 百拇医药
7.38
8.85
11.45
12.52
10.70
10.33
9.42
8.32
100.00
合 计
5.63
5.02
6.72
, 百拇医药
6.95
7.66
9.12
10.47
11.60
10.86
10.13
8.80
7.04
100.00
1.2 分析方法
应用圆形分布法[4]计算各月发病频数,求平均角
 =180°+arctg(Y/X),当本组X<0时;根据余弦模型和估计参数方法[5],由月发病数计算月构成比并转换成对数后建模,并据
=180°+arctg(Y/X),当本组X<0时;根据余弦模型和估计参数方法[5],由月发病数计算月构成比并转换成对数后建模,并据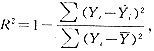 ,计算决定系数。2 结果与分析
,计算决定系数。2 结果与分析, 百拇医药
2.1 该区域狂犬病的季节性高峰特征明显
经圆形分布法分年度分析湖北省7年资料,1987~1991年季节性高峰特征极显著(r>r0.01(n),P<0.01),发病高峰时点比较一致,在8月9日至9月16日,表明将各年度资料合并计算具有代表意义。进而对各省和三省合并资料进行分析,集中趋势值r均大于0.001,P<0.001,见表2。
表2 不同时、空狂犬病的圆形分布法分析结果
年份
r
P
平均角
 (度)
(度), http://www.100md.com
发病高
峰日
湖北省
1987
0.1962
<0.001
240.34
9月1日
1988
0.1939
<0.001
222.29
8月13日
, http://www.100md.com
1989
0.1616
<0.001
255.27
9月16日
1990
0.1662
<0.001
221.64
8月13日
1991
0.1468
<0.01
, 百拇医药
217.70
8月9日
1987~93
0.1603
<0.001
228.60
8月20日
湖南省
1981~96
0.1428
<0.001
218.84
, 百拇医药 8月10日
河南省
1951~95
0.2107
<0.001
236.67
8月28日
合 计
0.1654
<0.001
230.20
8月21日
2.2 该区域狂犬病的发病高峰呈周期性、季节性分布符合余弦曲线模型
, 百拇医药
应用余弦模型分别对三省及其合并的月构成比进行对数拟合,据函数分程
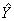 i=M+Acos(ωti-φ)分别建立简单余弦函数分程:
i=M+Acos(ωti-φ)分别建立简单余弦函数分程: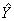 i(湘)=0.909+0.146cos(ti-204.88°) R2=0.9055
i(湘)=0.909+0.146cos(ti-204.88°) R2=0.9055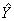 i(鄂)=0.907+0.149cos(ti-213.50°) R2=0.9064
i(鄂)=0.907+0.149cos(ti-213.50°) R2=0.9064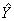 i(豫)=0.898+0.195cos(ti-220.77°) R2=0.9162
i(豫)=0.898+0.195cos(ti-220.77°) R2=0.9162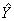 i(计)=0.906+0.153cos(ti-214.69°) R2=0.9595
i(计)=0.906+0.153cos(ti-214.69°) R2=0.9595, http://www.100md.com
决定系数R2在0.9055~0.9595之间,表明简单余弦模型拟合效果已经甚佳,不必再建三角多项式。据φ=210°相当于8月15日和模型中的φ值,说明发病高峰在8月中、下旬。因余弦曲线上下波动呈对称性,故φ-180°所对应的2月中、下旬为发病低谷。代入ti值后取反对数得各月构成比理论值,见表3。表3 湘、鄂、豫三省狂犬病月发病构成比简单余弦模型拟合的理论值 月份
i
t
湖 南
湖 北
河 南
合 计
Yi
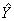 i
i, http://www.100md.com
Yi
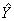 i
iYi
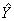 i
iYi
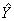 i
i1
0
5.76
6.04
6.64
, http://www.100md.com
6.06
4.70
5.63
5.63
6.03
2
30
5.45
5.79
4.31
5.73
4.54
5.09
, 百拇医药
5.02
5.67
3
60
7.29
6.08
6.79
5.94
5.44
5.17
6.72
5.86
4
, http://www.100md.com
90
7.34
6.89
6.54
6.68
6.35
5.90
6.95
6.59
5
120
7.57
8.16
, http://www.100md.com
8.42
7.91
7.38
7.27
7.66
7.83
6
150
9.10
9.65
9.64
9.41
8.85
, http://www.100md.com
9.17
9.12
9.36
7
180
10.01
10.89
10.50
10.74
11.45
11.11
10.47
10.76
, http://www.100md.com
8
210
11.46
11.35
10.60
11.37
12.52
12.29
11.60
11.44
9
240
10.88
, 百拇医药
10.81
11.05
10.97
10.70
12.08
10.86
11.07
10
270
10.18
9.64
9.64
9.76
, 百拇医药
10.33
10.60
10.13
9.84
11
300
8.60
8.06
8.52
8.24
9.42
8.60
8.80
, http://www.100md.com
8.29
12
330
6.36
6.82
7.35
6.93
8.32
6.82
7.04
6.93
2.3 不同地区发病高峰时点的比较
湘、鄂、豫三省紧密相连,基本在同一东经跨度不同北纬范围。圆形分布法分析和余弦模型拟合转换的发病高峰时点一致,分别为8月10日、8月20日和8月28日,表明三省的发病高峰的点比较一致。同时可见,在同一经度范围发病高峰的点由南到北逐渐推后8~10天。
, http://www.100md.com
2.4 狂犬病的季节性与流行强度有一定关系
将湖北省发病率较高前三年、发病率较低的后两年合并分析,以雷氏Z值[6]检验平均角。后两年的结果说明,虽然分年度分析散发年的高峰特征不显著,但合并分析同样显示出季节性高峰特征。同时可见,反映季节性强弱的雷氏Z值与发病率呈正相关(r=0.9526,P<0.01),发病高峰时点随发病率下降呈前移趋势,见表4。表4 不同发病率的雷氏Z值与发病高峰时点 年份
发病率
(/10万)
平均角

(度)
雷氏Z值
, http://www.100md.com
P
发病高
峰日
1987~89
0.78
241.42
12.78
<0.001
9月2日
1990
0.59
221.64
8.59
, 百拇医药
<0.001
8月13日
1991
0.46
217.70
5.35
<0.01
8月9日
1992~93
0.19
180.23
3.74
<0.05
, 百拇医药
7月2日
3 讨论
圆形分布法分析疾病季节性的重要特点是能用平均角的检验判断疾病的季节性,余弦模型则能反映和预测疾病在全年各月的分布。本文通过一定区域较大样本的不同时、空的分析,证明狂犬病具有明显的季节性高峰特征,其分布符合余弦典线模型。圆形分布法与周期性回归分析,一致表明该区域狂犬病的发病高峰在8月中、下旬、发病低谷在2月中、下旬。
湘、鄂、豫三省狂犬病的发病高峰时点和由南到北的先后差距,反映高峰期前的气温是主要影响因素;分年段分析反映季节性与流行强度有关,提示在一些发病率低的地区,可能季节性高峰特征表现不明显。
将狂犬病的季节性分布建立成数学模型、发病高峰与低谷计算到月、日,还仅仅是尝试。与狂犬病无明显的季节性高峰、与春、夏、秋较多、冬季较少的持续高峰[2,7]等结论均有分歧。所以,关于狂犬病的季节性问题,还需要进一步研究论证。本文未进行样本角均数间的显著性检验,是因为受到圆形分布法中F检验的条件限制。
, http://www.100md.com
参考文献
1 郭绶衡,刘文,李树民,等.湖北省1951~1996年人间狂犬病流行病学分析.中国人兽共患病杂志,1998,14(1):78~78.
2 林放涛,于恩庶主编.狂犬病学.福建:福建科学技术出版社,1992,120~133.
3 张彦平,李林村,芮春军,等.河南省狂犬病流行病学分析.中国人兽共患病杂志,1998,14(3):74~76.
4 郭祖超主编.医用数理统计方法.北京:人民卫生出版社,1988,132~139.
5 胡克震,姜芝莉.周期性回归.中华预防医学杂志,1988,22(1):22~25.
6 金丕焕主编.医用统计方法.上海:上海医科大学出版社,1993,210~211.
7 夏祝辉主编.流行病学及传染病管理.北京:人民卫生出版社,1990,290.
收稿日期:1999-04-11, 百拇医药