准确检测心电信号中的QRS复合波方法的研究
作者:阙向红 胡 彬 郭小梅
单位:同济医科大学计算中心 武汉430030
关键词:心电信号;QRS复合波;自动检测
数理医药学杂志990412 摘 要 提出了一种具有抗干扰(如肌电干扰、交流干扰、基线漂移等)性能强、简单实用、不失真的检测方法,经过实测,对干扰较小、形态正常的心电波形识别达100%,而对存在较大干扰的心电波形识别也可达到96%以上。
1 问题提出
心血管疾病是威胁人类生命的最主要疾病之一,而心电信号(ECG)是诊断心血管疾病的主要依据。目前普通心电检查已成为各大小医院的常规检查手段,床边连续计算机监护技术、运动心电向量计算机自动分析技术、动态ECG计算机监护技术等近年来也得到了广泛使用,且已成为诊断各种心血管疾病、评价各种心血管药物的疗效、监测起博器功能等临床情况的一种重要手段,越来越受到临床医师的高度重视。
, 百拇医药
上述各种检查手段与技术都必须对ECG进行自动分析,而QRS波的检测则是ECG自动分析的基础。对QRS波的检测一般使用等值、差分、模板、曲线拟合等方法,这些方法在实际使用中,对心电信号中出现的强工频干扰,尤其是对运动心电信号中较强的肌电干扰、严重的基线漂移,波形的形态变异等,均在不同的程度上存在着波形失真、识别的准确率不高等弱点。
由于运动心电信号干扰太大造成了QRS波准确识别的难度。作者在开发运动心电向量图计算机自动识别的研制中,提出了一种识别方法。经过反复验证,该方法在静态心电向量的自动分析中获得了非常满意的结果,尤其是在运动心电向量图的自动分析中,本方法与弱数字滤波方法的配合,在QRS波形不失真的情况下,表现出很强的抗干扰性能,大大提高了QRS复合波识别的准确率。
2 方法介绍
2.1 弱数字滤波
在精度为12位、采样频率为1000Hz的数据采集系统下,对采集的心电信号进行三点或五点的平滑数字滤波,可消除波形上的尖刺。因为这种滤波方法对QRS波的幅度与宽度的影响非常小,可忽略不计,同时又能消除波形上对波形识别造成影响的较为突出的尖刺,这给本文所提出的方法对QRS复合波中的R波或者其它波(如Q波、S'波、R'波、S波)的准确识别奠定了基础。
, 百拇医药
2.2 利用点线距离法识别QRS复合波
在经过弱数字滤波的心电波形上,开一个长度为N(N必须为奇数)个采样点的波形识别平面窗口,在窗口的第一点与最末点之间作一条连线,求出窗口的中点M到连线的距离D(见图1):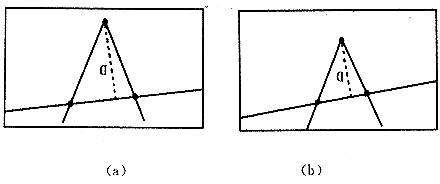
图1 假设识别窗口的长度为15
如果窗口的中点满足下列两个条件:
①D为最大值且大于等于所设定的阀值Fd
②对于图1a,M左边的点为非连续递增,其右边的点为非连续递减;对于图1b,M左边的点为非连续递减,其右边的点为非连续递增。
则我们认为M应是QRS复合波中的某一个波的顶点(为了方便叙述,我们把波峰的最高点或波谷的最低点统称为顶点),只要将窗口从QRS波的起始点开始,平滑移动到波形的最末点,就能得到数个波的顶点。若波的顶点的总数大于5,则说明窗口的长度或者预定的阀值Fd不合适,利用QRS波的波峰与波谷的特征较为明显的特点,经过自动调整,再重复上述的计算与判断,即可得到合适的结果。
, 百拇医药
这种利用平面上点到直线的距离识别QRS复合波的几何算法可检测各种形态变异的QRS波。
2.3 遗漏波的检测
在本方法中,阀值Fd是针对R波或者R波、S波、R'波所设计的,因此,需要检测可能遗漏的Q波、S波或者Q波、S'波,由于篇幅所限,遗漏波的检测算法在此省略。
2.4 QRS波的起始点与终止点的识别
为了方便叙述,现以图2为例,通过Q波的顶点作一条夹角为α(α的值在135℃到155℃之间)的直线,通过S波(或者S'波)的顶点作一条夹角为β(β的值在35℃到55℃之间)的直线(见图2):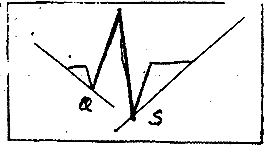
图2 QRS波的起始点与终止点的识别
, 百拇医药
假设(Xq,Yq)为Q波的顶点,令:
K=tgα B=Yq-KXq (1)
则该直线方程为:
Y=KX+B
又假设(Xi,Yi)为参与计算点的坐标,然后利用公式: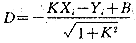 (2)
(2)
求出点(Xi,Yi)到直连线的距离,其中对D的符号作如下规定:
①如参与计算点位于直线的上方,则D为正
, 百拇医药
②如参与计算点位于直线的下方,则D为负
参与计算点应从Q波的顶点开始,逐点向P波的方向移动,这样可得到一系列的D值,这些D值的最大值所对应的点即为QRS波的起始点。
在本系统中,为加快公式(1)和公式(2)浮点运算的计算速度,当连续若干点的D值为负值时,即中止计算。
同理,可计算出QRS波的终止点。
3 结束语
由于本文所述方法采用了弱数字滤皮方法,因而波形的失真(如QRS波的幅度被削减,QRS波的宽度被增加等)非常小,可忽略不计。且把QRS波放在一个几何平面上,并利用平面的局部区域对心电信号基线漂移的不敏感性,点到直线的解析几何算法对交流干扰、肌电干扰的不敏感性,使其实用性得到了增强,准确性得到了提高。因此,本文对寻找具有抗干扰能力的心电信号识别算法做了一次建设性的探索。
, 百拇医药
作者简介:郭小梅 同济医科大学附属同济医院
参考文献
1 M.Friesen et al. A comparison of the noise sensitivity of nine QRS detection algorithms, IEEE trans on BME, 1990,37(1).
2 L.Kennedy et al. Ambulatory(Holter) ECG using real-time analysis, The American Journalcardiology, 1987,59(5).
3 Fraden et al. QRS Wave detecter, Mes & Biol. &Comput,1980(3).
4 田立军等.一种检测与分析QRS波的算法.中国医疗器械杂志,1992,16(3).
5 谭义等.微机心律失常自动分析程序的研究.成都电讯工程学院学报,1985(3).
6 郑启宇等.心律失常心电图诊断与治疗.湖南科学技术出版社,1979.
7 戚建新等.基于微机的心电信号实时处动分析系统.中国医药信息学会CMIA’97河北.承德.
收稿日期:1999-01-24, 百拇医药
单位:同济医科大学计算中心 武汉430030
关键词:心电信号;QRS复合波;自动检测
数理医药学杂志990412 摘 要 提出了一种具有抗干扰(如肌电干扰、交流干扰、基线漂移等)性能强、简单实用、不失真的检测方法,经过实测,对干扰较小、形态正常的心电波形识别达100%,而对存在较大干扰的心电波形识别也可达到96%以上。
1 问题提出
心血管疾病是威胁人类生命的最主要疾病之一,而心电信号(ECG)是诊断心血管疾病的主要依据。目前普通心电检查已成为各大小医院的常规检查手段,床边连续计算机监护技术、运动心电向量计算机自动分析技术、动态ECG计算机监护技术等近年来也得到了广泛使用,且已成为诊断各种心血管疾病、评价各种心血管药物的疗效、监测起博器功能等临床情况的一种重要手段,越来越受到临床医师的高度重视。
, 百拇医药
上述各种检查手段与技术都必须对ECG进行自动分析,而QRS波的检测则是ECG自动分析的基础。对QRS波的检测一般使用等值、差分、模板、曲线拟合等方法,这些方法在实际使用中,对心电信号中出现的强工频干扰,尤其是对运动心电信号中较强的肌电干扰、严重的基线漂移,波形的形态变异等,均在不同的程度上存在着波形失真、识别的准确率不高等弱点。
由于运动心电信号干扰太大造成了QRS波准确识别的难度。作者在开发运动心电向量图计算机自动识别的研制中,提出了一种识别方法。经过反复验证,该方法在静态心电向量的自动分析中获得了非常满意的结果,尤其是在运动心电向量图的自动分析中,本方法与弱数字滤波方法的配合,在QRS波形不失真的情况下,表现出很强的抗干扰性能,大大提高了QRS复合波识别的准确率。
2 方法介绍
2.1 弱数字滤波
在精度为12位、采样频率为1000Hz的数据采集系统下,对采集的心电信号进行三点或五点的平滑数字滤波,可消除波形上的尖刺。因为这种滤波方法对QRS波的幅度与宽度的影响非常小,可忽略不计,同时又能消除波形上对波形识别造成影响的较为突出的尖刺,这给本文所提出的方法对QRS复合波中的R波或者其它波(如Q波、S'波、R'波、S波)的准确识别奠定了基础。
, 百拇医药
2.2 利用点线距离法识别QRS复合波
在经过弱数字滤波的心电波形上,开一个长度为N(N必须为奇数)个采样点的波形识别平面窗口,在窗口的第一点与最末点之间作一条连线,求出窗口的中点M到连线的距离D(见图1):

图1 假设识别窗口的长度为15
如果窗口的中点满足下列两个条件:
①D为最大值且大于等于所设定的阀值Fd
②对于图1a,M左边的点为非连续递增,其右边的点为非连续递减;对于图1b,M左边的点为非连续递减,其右边的点为非连续递增。
则我们认为M应是QRS复合波中的某一个波的顶点(为了方便叙述,我们把波峰的最高点或波谷的最低点统称为顶点),只要将窗口从QRS波的起始点开始,平滑移动到波形的最末点,就能得到数个波的顶点。若波的顶点的总数大于5,则说明窗口的长度或者预定的阀值Fd不合适,利用QRS波的波峰与波谷的特征较为明显的特点,经过自动调整,再重复上述的计算与判断,即可得到合适的结果。
, 百拇医药
这种利用平面上点到直线的距离识别QRS复合波的几何算法可检测各种形态变异的QRS波。
2.3 遗漏波的检测
在本方法中,阀值Fd是针对R波或者R波、S波、R'波所设计的,因此,需要检测可能遗漏的Q波、S波或者Q波、S'波,由于篇幅所限,遗漏波的检测算法在此省略。
2.4 QRS波的起始点与终止点的识别
为了方便叙述,现以图2为例,通过Q波的顶点作一条夹角为α(α的值在135℃到155℃之间)的直线,通过S波(或者S'波)的顶点作一条夹角为β(β的值在35℃到55℃之间)的直线(见图2):

图2 QRS波的起始点与终止点的识别
, 百拇医药
假设(Xq,Yq)为Q波的顶点,令:
K=tgα B=Yq-KXq (1)
则该直线方程为:
Y=KX+B
又假设(Xi,Yi)为参与计算点的坐标,然后利用公式:
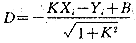 (2)
(2)求出点(Xi,Yi)到直连线的距离,其中对D的符号作如下规定:
①如参与计算点位于直线的上方,则D为正
, 百拇医药
②如参与计算点位于直线的下方,则D为负
参与计算点应从Q波的顶点开始,逐点向P波的方向移动,这样可得到一系列的D值,这些D值的最大值所对应的点即为QRS波的起始点。
在本系统中,为加快公式(1)和公式(2)浮点运算的计算速度,当连续若干点的D值为负值时,即中止计算。
同理,可计算出QRS波的终止点。
3 结束语
由于本文所述方法采用了弱数字滤皮方法,因而波形的失真(如QRS波的幅度被削减,QRS波的宽度被增加等)非常小,可忽略不计。且把QRS波放在一个几何平面上,并利用平面的局部区域对心电信号基线漂移的不敏感性,点到直线的解析几何算法对交流干扰、肌电干扰的不敏感性,使其实用性得到了增强,准确性得到了提高。因此,本文对寻找具有抗干扰能力的心电信号识别算法做了一次建设性的探索。
, 百拇医药
作者简介:郭小梅 同济医科大学附属同济医院
参考文献
1 M.Friesen et al. A comparison of the noise sensitivity of nine QRS detection algorithms, IEEE trans on BME, 1990,37(1).
2 L.Kennedy et al. Ambulatory(Holter) ECG using real-time analysis, The American Journalcardiology, 1987,59(5).
3 Fraden et al. QRS Wave detecter, Mes & Biol. &Comput,1980(3).
4 田立军等.一种检测与分析QRS波的算法.中国医疗器械杂志,1992,16(3).
5 谭义等.微机心律失常自动分析程序的研究.成都电讯工程学院学报,1985(3).
6 郑启宇等.心律失常心电图诊断与治疗.湖南科学技术出版社,1979.
7 戚建新等.基于微机的心电信号实时处动分析系统.中国医药信息学会CMIA’97河北.承德.
收稿日期:1999-01-24, 百拇医药