利用电位滴定的数据拟合滴定曲线并计算滴定等当点及其计算程序
作者:李静莉 张丽英 蒋海松 刘树春
单位:黑龙江省药品检验所 哈尔滨150001
关键词:电位滴定;等当点;E-V曲线方程的参数;BASIC程序
数理医药学杂志990411
摘 要 用S型曲线拟合的方法计算电位滴定的等当点,能更快速准确的解决电位滴定中样品颜色干扰和等当点时电位突跃不明显的情况。
在电位滴定中,测得n对数据,以此数据确定E-V曲线方程及曲线方程中的参数。依据参数计算滴定等当点的方法是一种准确而有效的方法。在国内有关资料[1]中用三次曲线方程拟合,但典型的滴定曲线提S形曲线,所以本文给出S形曲线方程,来拟合电位滴定曲线,以及由此求出等当点。本文还附有这种方法的BASIC语言计算程序,为滴定等当点的计算提供了简便有效的手段。
, 百拇医药
1 E-V曲线方程
以滴定剂体积V为横座标,电位E为纵座标的曲线是E-V曲线。E-V曲线通常呈S型,它的方程具有如下形式: (1)
(1)
其中a、b是方程(1)的参数。当参数a、b已知后,E-V曲线的形状就确定了。
用回归分析可确定参数a、b。首先将方程(1)线性化,令Y=1/E,X=e-v,方程(1)化为X与Y的线性方程:
Y=a+bX (2)
在滴定时,测得V和E的n对数据(Vi,Ei)i=1,2,…n,从而求得X和Y的n对数(Xi,Yi),这里Xi=e-vi,Yi=1/Ei,依据最小二乘法原理估计参数a、b的值为: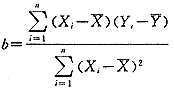 (3)
(3) (4)
(4)
, 百拇医药
其中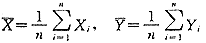
对回归直线方程(2)进行相关性检验,选取统计量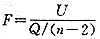 (5)
(5)
其中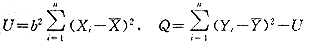
查F分布表,找出临界值F0.05(1,n-2)。若F>F0.05(1,n-2),则认为X与Y之间存在线性相关关系,回归直线方程(2)有意义,所求参数a、b值可相信,因此方程(1)有意义。它就是要求的E-V曲线方程。
2 等当点的计算
等当点是E-V曲线上拐点的横座标,因此在等当点处电位E的二阶微商等于零,即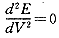 (6)
(6)
, 百拇医药
在方程(1)有意义时,公式(6)即为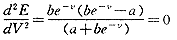
因为e-v≠0,所以be-v-a=0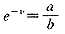
于是 (7)
(7)
其中a、b由公式(3)、(4)计算,公式(7)为所求的等当点。
3 程序流程图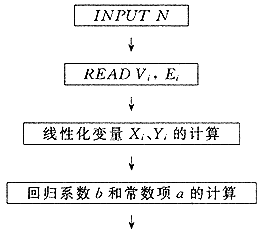

, 百拇医药
4 实例
典型的酸碱滴定曲线用自动滴定仪(METTLER DL25型 Titrator)滴定,结果等当点时的体积为8.758。而本文拟合曲线及计算程序运行结果等当点时的体积为8.755,两者结果基本一致,说明本文拟合曲线及运行程序合理可行。
5 讨论
5.1 本文用S形曲线拟合,因此适用于一个滴定等当点情形。
5.2 当F不满足条件时,可适当增加测定点数,以反映滴定过程的特征。如起始数据随体积变化,电位变化不明显时可适当删除起始的几组数据。当增加测定点数仍不满足条件时,可修正方程。
5.3 在分析实验中,用指示剂判断滴定终点时,经常受到溶液带有颜色及辅料的浑浊影响而使终点难以判断。电位滴定则可准确地确定等当点。随着计算机的普及与推广,用计算机处理复杂的实验数据更简单、方便。根据实验数据拟合的曲线求出的等当点更为精确,并且滴定过程不受等体积的限制即可算出等当点。
作者简介:刘树春 天津市药品检验所
参考文献
1 袁萌棠.概率论与数理统计.中国人民大学出版社,1993,216~217.
收稿日期:1999-01-24, 百拇医药
单位:黑龙江省药品检验所 哈尔滨150001
关键词:电位滴定;等当点;E-V曲线方程的参数;BASIC程序
数理医药学杂志990411
摘 要 用S型曲线拟合的方法计算电位滴定的等当点,能更快速准确的解决电位滴定中样品颜色干扰和等当点时电位突跃不明显的情况。
在电位滴定中,测得n对数据,以此数据确定E-V曲线方程及曲线方程中的参数。依据参数计算滴定等当点的方法是一种准确而有效的方法。在国内有关资料[1]中用三次曲线方程拟合,但典型的滴定曲线提S形曲线,所以本文给出S形曲线方程,来拟合电位滴定曲线,以及由此求出等当点。本文还附有这种方法的BASIC语言计算程序,为滴定等当点的计算提供了简便有效的手段。
, 百拇医药
1 E-V曲线方程
以滴定剂体积V为横座标,电位E为纵座标的曲线是E-V曲线。E-V曲线通常呈S型,它的方程具有如下形式:
 (1)
(1)其中a、b是方程(1)的参数。当参数a、b已知后,E-V曲线的形状就确定了。
用回归分析可确定参数a、b。首先将方程(1)线性化,令Y=1/E,X=e-v,方程(1)化为X与Y的线性方程:
Y=a+bX (2)
在滴定时,测得V和E的n对数据(Vi,Ei)i=1,2,…n,从而求得X和Y的n对数(Xi,Yi),这里Xi=e-vi,Yi=1/Ei,依据最小二乘法原理估计参数a、b的值为:
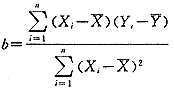 (3)
(3) (4)
(4), 百拇医药
其中
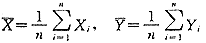
对回归直线方程(2)进行相关性检验,选取统计量
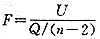 (5)
(5)其中
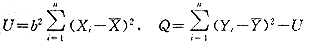
查F分布表,找出临界值F0.05(1,n-2)。若F>F0.05(1,n-2),则认为X与Y之间存在线性相关关系,回归直线方程(2)有意义,所求参数a、b值可相信,因此方程(1)有意义。它就是要求的E-V曲线方程。
2 等当点的计算
等当点是E-V曲线上拐点的横座标,因此在等当点处电位E的二阶微商等于零,即
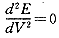 (6)
(6), 百拇医药
在方程(1)有意义时,公式(6)即为
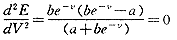
因为e-v≠0,所以be-v-a=0
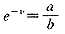
于是
 (7)
(7)其中a、b由公式(3)、(4)计算,公式(7)为所求的等当点。
3 程序流程图


, 百拇医药
4 实例
典型的酸碱滴定曲线用自动滴定仪(METTLER DL25型 Titrator)滴定,结果等当点时的体积为8.758。而本文拟合曲线及计算程序运行结果等当点时的体积为8.755,两者结果基本一致,说明本文拟合曲线及运行程序合理可行。
5 讨论
5.1 本文用S形曲线拟合,因此适用于一个滴定等当点情形。
5.2 当F不满足条件时,可适当增加测定点数,以反映滴定过程的特征。如起始数据随体积变化,电位变化不明显时可适当删除起始的几组数据。当增加测定点数仍不满足条件时,可修正方程。
5.3 在分析实验中,用指示剂判断滴定终点时,经常受到溶液带有颜色及辅料的浑浊影响而使终点难以判断。电位滴定则可准确地确定等当点。随着计算机的普及与推广,用计算机处理复杂的实验数据更简单、方便。根据实验数据拟合的曲线求出的等当点更为精确,并且滴定过程不受等体积的限制即可算出等当点。
作者简介:刘树春 天津市药品检验所
参考文献
1 袁萌棠.概率论与数理统计.中国人民大学出版社,1993,216~217.
收稿日期:1999-01-24, 百拇医药