建立回归模型应注意避免多重共线性
作者:王 伟 田庆伟
单位:天津医科大学卫生统计教研室 天津300070
关键词:
数理医药学杂志9904101 问题的提出
多元回归分析是一种应用广泛的多变量分析方法。但是如果对变量的条件不加任何考虑,盲目地应用现成的统计软件包,往往得不到理想的结果,甚至导致错误的结论。为了保证所得回归模型有较好的应用效果,近年来多重共线性的研究已受到关注。应用多元回归的前提是有关自变量必须是相互独立的。但是,事实上,在医学领域内各变量间相关的情况大量存在。例如在病因流行病学研究中的多种危险因素之间常会存在一定程度的相关关系,出现统计学上所谓的多重共线性。如果各个危险因素的内在相关程度较大时,在进行回归分析过程中,一个危险因素可能取代另一个危险因素,或相互抵消其对应变量的影响,使原来有显著性的危险因素变得无显著性意义,而使结果难以解释[1]。
, 百拇医药
多重共线性是指一些自变量或全部自变量存在高度相关,即这些自变量之间有近似线性关系,这时求得的回归系数值不稳定且难于解释。严重的是全部自变量有高度近似的线性关系,这时自变量相关矩阵的行列式近似等于零,为奇异矩阵,解不出逆矩阵,因而求不出回归系数值。
那么,如何避免多重共线性的发生,即如何及时识别两解释变量是否高度相关,以便剔除其中一个变量,以求得模型的准确呢?在一些受到普遍应用的统计软件中,都设有这方面的分析程序。因此弄清其诊断方法,正确地运用所输出的指标,无疑是很有意义的[2]。本文介绍一种比较实用的方法,即通路分析法。
2 方法介绍
通路分析是继回归分析之后发展起来的一种统计方法,它不但是作为线性回归模型的补充,更重要的是作为线性回归模型的发展。通路分析用通路图不仅把自变量和应变量之间数量关系的描述形象化,而且使描述内容更加丰富和描述范围更加扩大[3]。通路图用偏回归系数比较各自变量对应变量的直接作用,通路图还利用了两两变量间的相关系数,又可比较各自变量通过其他自变量对应变量的间接作用,找到由于自变量间的相关性导致多重共线性的自变量。但是,如果不进行前期共线性检验而直接求解偏回归系数,则使计算所得值并不反映真实的直接影响,而是包含了间接影响,即包含了某一自变量通过另一自变量对应变量的影响,使得求解出的方程失去使用价值。因此应在求解方程之前对各自变量分析测定其对应变量的直接影响和间接影响,一旦出现间接影响非常大,说明该因素对应变量的直接因果作用小,它是通过影响其它自变量而间接影响着应变量的。这就形成了该因素与其它自变量因素间存在的高度共线性。那么,就需要剔除该因素,以求得真实的回归方程。
, 百拇医药
多重共线性的检验步骤如下:
①由常规简单相关系数法求两两变量间的相关系数;
②作通路图;
③求解通路系数,即标准化的偏回归系数;
④剖分原因和结果间相关系数,即直接影响和间接影响,寻找引起多重共线性的自变量;
⑤结论。
3 实例分析
为了解儿童社会生活能力与其个性特征间的关系,我们对340名8~12岁的儿童采用社会生活能力量表进行调查。该量表由独立生活能力(SH)、运动能力(L)、作业能力(O)、交往能力(C)、参加集体活动能力(S)及自我管理能力(SD)六项组成。并用艾森克问卷进行个性测验。由性格内外向(E)、情绪稳定性(N)、精神质(P)及掩饰性(LL)四项组成。
, 百拇医药
3.1 根据调查结果计算简单相关系数,结果见表1。
表1 变量间的相关系数
SH
L
O
C
S
SD
E
SH
1.0000
0.7077
0.7540
, 百拇医药
0.7710
0.7577
0.8263
0.4889
L
1.0000
0.7626
0.7682
0.7657
0.6971
0.6128
O
1.0000
, 百拇医药
0.7387
0.7226
0.7053
0.5487
C
1.0000
0.8359
0.8343
0.6091
S
1.0000
0.7947
0.5092
, 百拇医药
SD
1.0000
0.5007
E
1.0000
3.2 作通路图(略)。
3.3 建立方程求解通路系数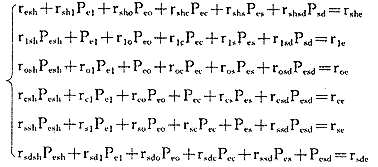
将表1结果代入方程组解方程,得通路系数:PYXi=Xi对Y的直接影响(也称通路系数)
Pesh=0.099417
, http://www.100md.com
Pe1=0.332342
Peo=0.174269
Pec=0.781281
Pes=-0.369296
Pesd=-0.334826
rXiXjPYXj=Xi通过Xj对Y的间接影响
∑rXiXjPYXj=Xj对Y的总间接影响
, 百拇医药
rXiY=Xi对Y直接与间接影响总和
即相关系数=直接影响+间接影响
由此可以看出,某一个自变量Xi与应变量Y的相关性取决于两方面的效应:一是通路系数PYXi,表示Xi对Y的直接影响;二是自变量间的相关系数rXiYj表示自变量间的联合作用,称为间接影响。所以,PYXi=rXiY-∑rXiXjPYXj。
若自变量间相关系数很高,必然导致通路系数的符号发生改变,这就是多元共线性现象。
, http://www.100md.com
3.4 剖分原因,寻找引起多重共线性的自变量
根据以上公式,对该例进行相关关系的剖分,通路分析可以把某一个自变量与应变量间相关系数剖分为两部分:直接影响与间接影响,并找出引起多重共线性的自变量。
由表2分析结果可看出,简单相关系数与通路系数不尽相同,有的甚至符号相反。最明显的是参加集体活动能力(S)与性格内外向(E)的简单相关系数为0.5586,而通路系数为-0.3693;同样地,自我管理能力(SD)与性格内外向(E)的简单相关系数为0.5511,而通路系数为-0.3348。这意味着表面上参加集体活动能力(S)与性格内外向(E)间及自我管理能力(SD)与性格内外向(E)有中等程度的相关关系,实际上是通过交往能力(C)起的作用。导致相关系数出现负值与实际意义不符的原因是因为C与S及C与SD间的相关系数过高,均大于0.83,由此可判断S、SD是引起多重共线性的变量。表2 性格内外向影响因素的通路分析 变量
, http://www.100md.com
总影响
直接影响
间 接 影 响
总的
通过SH
通过L
通过O
通过C
通过S
通过SD
SH
0.5119
0.0994
, http://www.100md.com
0.4125
0.2352
0.1314
0.6023
-0.2798
-0.2766
L
0.6196
0.3323
0.2872
0.0703
0.1329
, 百拇医药 0.6002
-0.2828
-0.2334
O
0.5768
0.1743
0.4024
0.0749
0.2534
0.5771
-0.2669
-0.2361
C
, 百拇医药
0.6526
0.7813
-0.1286
0.0766
0.2553
0.1288
-0.3100
-0.2793
S
0.5586
-0.3693
0.9280
, 百拇医药 0.0753
0.2544
0.1259
0.6559
-0.1837
SD
0.5511
-0.3348
0.8858
0.0821
0.2316
0.1229
0.6518
, 百拇医药
-0.2026
4 结论
交往能力(C)因其直接影响值为0.7813,远远大与其它各因素的直接影响程度,因而是影响性格内外向(E)的最重要的因素。运动能力(L)、作业能力(O)对E的影响分列其后。独立生活能力(SH)的直接影响很小(0.0994),而参加集体活动能力(S)及自我管理能力(SD)的直接影响均为负值(-0.3693及-0.3348),说明间接影响作用变量非常大。为了更科学、准确地分析各因素对性格内外向的影响,应剔除发生多重共线性的参加集体活动能力(S)及自我管理能力(SD),利用交往能力(C)、运动能力(L)、作用能力(O)及独立生活能力(SH)建立求性格内外向(E)的回归方程。
参考文献
1 童身以等.多元共线性数据的处理.中国卫生统计,1995,12(1):40~41.
2 柳丽等.回归分析中的多重共线性的诊断与处理.中国卫生统计,1994,11(1):5~7.
3 潘耀东.通径分析在乙脑流行因素分析中的应用.中国卫生统计,1994,11(1):30~31.
收稿日期:1999-03-07, 百拇医药
单位:天津医科大学卫生统计教研室 天津300070
关键词:
数理医药学杂志9904101 问题的提出
多元回归分析是一种应用广泛的多变量分析方法。但是如果对变量的条件不加任何考虑,盲目地应用现成的统计软件包,往往得不到理想的结果,甚至导致错误的结论。为了保证所得回归模型有较好的应用效果,近年来多重共线性的研究已受到关注。应用多元回归的前提是有关自变量必须是相互独立的。但是,事实上,在医学领域内各变量间相关的情况大量存在。例如在病因流行病学研究中的多种危险因素之间常会存在一定程度的相关关系,出现统计学上所谓的多重共线性。如果各个危险因素的内在相关程度较大时,在进行回归分析过程中,一个危险因素可能取代另一个危险因素,或相互抵消其对应变量的影响,使原来有显著性的危险因素变得无显著性意义,而使结果难以解释[1]。
, 百拇医药
多重共线性是指一些自变量或全部自变量存在高度相关,即这些自变量之间有近似线性关系,这时求得的回归系数值不稳定且难于解释。严重的是全部自变量有高度近似的线性关系,这时自变量相关矩阵的行列式近似等于零,为奇异矩阵,解不出逆矩阵,因而求不出回归系数值。
那么,如何避免多重共线性的发生,即如何及时识别两解释变量是否高度相关,以便剔除其中一个变量,以求得模型的准确呢?在一些受到普遍应用的统计软件中,都设有这方面的分析程序。因此弄清其诊断方法,正确地运用所输出的指标,无疑是很有意义的[2]。本文介绍一种比较实用的方法,即通路分析法。
2 方法介绍
通路分析是继回归分析之后发展起来的一种统计方法,它不但是作为线性回归模型的补充,更重要的是作为线性回归模型的发展。通路分析用通路图不仅把自变量和应变量之间数量关系的描述形象化,而且使描述内容更加丰富和描述范围更加扩大[3]。通路图用偏回归系数比较各自变量对应变量的直接作用,通路图还利用了两两变量间的相关系数,又可比较各自变量通过其他自变量对应变量的间接作用,找到由于自变量间的相关性导致多重共线性的自变量。但是,如果不进行前期共线性检验而直接求解偏回归系数,则使计算所得值并不反映真实的直接影响,而是包含了间接影响,即包含了某一自变量通过另一自变量对应变量的影响,使得求解出的方程失去使用价值。因此应在求解方程之前对各自变量分析测定其对应变量的直接影响和间接影响,一旦出现间接影响非常大,说明该因素对应变量的直接因果作用小,它是通过影响其它自变量而间接影响着应变量的。这就形成了该因素与其它自变量因素间存在的高度共线性。那么,就需要剔除该因素,以求得真实的回归方程。
, 百拇医药
多重共线性的检验步骤如下:
①由常规简单相关系数法求两两变量间的相关系数;
②作通路图;
③求解通路系数,即标准化的偏回归系数;
④剖分原因和结果间相关系数,即直接影响和间接影响,寻找引起多重共线性的自变量;
⑤结论。
3 实例分析
为了解儿童社会生活能力与其个性特征间的关系,我们对340名8~12岁的儿童采用社会生活能力量表进行调查。该量表由独立生活能力(SH)、运动能力(L)、作业能力(O)、交往能力(C)、参加集体活动能力(S)及自我管理能力(SD)六项组成。并用艾森克问卷进行个性测验。由性格内外向(E)、情绪稳定性(N)、精神质(P)及掩饰性(LL)四项组成。
, 百拇医药
3.1 根据调查结果计算简单相关系数,结果见表1。
表1 变量间的相关系数
SH
L
O
C
S
SD
E
SH
1.0000
0.7077
0.7540
, 百拇医药
0.7710
0.7577
0.8263
0.4889
L
1.0000
0.7626
0.7682
0.7657
0.6971
0.6128
O
1.0000
, 百拇医药
0.7387
0.7226
0.7053
0.5487
C
1.0000
0.8359
0.8343
0.6091
S
1.0000
0.7947
0.5092
, 百拇医药
SD
1.0000
0.5007
E
1.0000
3.2 作通路图(略)。
3.3 建立方程求解通路系数
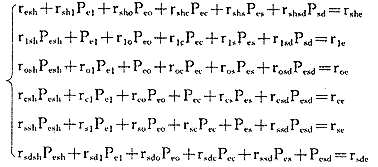
将表1结果代入方程组解方程,得通路系数:PYXi=Xi对Y的直接影响(也称通路系数)
Pesh=0.099417
, http://www.100md.com
Pe1=0.332342
Peo=0.174269
Pec=0.781281
Pes=-0.369296
Pesd=-0.334826
rXiXjPYXj=Xi通过Xj对Y的间接影响
∑rXiXjPYXj=Xj对Y的总间接影响
, 百拇医药
rXiY=Xi对Y直接与间接影响总和
即相关系数=直接影响+间接影响
由此可以看出,某一个自变量Xi与应变量Y的相关性取决于两方面的效应:一是通路系数PYXi,表示Xi对Y的直接影响;二是自变量间的相关系数rXiYj表示自变量间的联合作用,称为间接影响。所以,PYXi=rXiY-∑rXiXjPYXj。
若自变量间相关系数很高,必然导致通路系数的符号发生改变,这就是多元共线性现象。
, http://www.100md.com
3.4 剖分原因,寻找引起多重共线性的自变量
根据以上公式,对该例进行相关关系的剖分,通路分析可以把某一个自变量与应变量间相关系数剖分为两部分:直接影响与间接影响,并找出引起多重共线性的自变量。
由表2分析结果可看出,简单相关系数与通路系数不尽相同,有的甚至符号相反。最明显的是参加集体活动能力(S)与性格内外向(E)的简单相关系数为0.5586,而通路系数为-0.3693;同样地,自我管理能力(SD)与性格内外向(E)的简单相关系数为0.5511,而通路系数为-0.3348。这意味着表面上参加集体活动能力(S)与性格内外向(E)间及自我管理能力(SD)与性格内外向(E)有中等程度的相关关系,实际上是通过交往能力(C)起的作用。导致相关系数出现负值与实际意义不符的原因是因为C与S及C与SD间的相关系数过高,均大于0.83,由此可判断S、SD是引起多重共线性的变量。表2 性格内外向影响因素的通路分析 变量
, http://www.100md.com
总影响
直接影响
间 接 影 响
总的
通过SH
通过L
通过O
通过C
通过S
通过SD
SH
0.5119
0.0994
, http://www.100md.com
0.4125
0.2352
0.1314
0.6023
-0.2798
-0.2766
L
0.6196
0.3323
0.2872
0.0703
0.1329
, 百拇医药 0.6002
-0.2828
-0.2334
O
0.5768
0.1743
0.4024
0.0749
0.2534
0.5771
-0.2669
-0.2361
C
, 百拇医药
0.6526
0.7813
-0.1286
0.0766
0.2553
0.1288
-0.3100
-0.2793
S
0.5586
-0.3693
0.9280
, 百拇医药 0.0753
0.2544
0.1259
0.6559
-0.1837
SD
0.5511
-0.3348
0.8858
0.0821
0.2316
0.1229
0.6518
, 百拇医药
-0.2026
4 结论
交往能力(C)因其直接影响值为0.7813,远远大与其它各因素的直接影响程度,因而是影响性格内外向(E)的最重要的因素。运动能力(L)、作业能力(O)对E的影响分列其后。独立生活能力(SH)的直接影响很小(0.0994),而参加集体活动能力(S)及自我管理能力(SD)的直接影响均为负值(-0.3693及-0.3348),说明间接影响作用变量非常大。为了更科学、准确地分析各因素对性格内外向的影响,应剔除发生多重共线性的参加集体活动能力(S)及自我管理能力(SD),利用交往能力(C)、运动能力(L)、作用能力(O)及独立生活能力(SH)建立求性格内外向(E)的回归方程。
参考文献
1 童身以等.多元共线性数据的处理.中国卫生统计,1995,12(1):40~41.
2 柳丽等.回归分析中的多重共线性的诊断与处理.中国卫生统计,1994,11(1):5~7.
3 潘耀东.通径分析在乙脑流行因素分析中的应用.中国卫生统计,1994,11(1):30~31.
收稿日期:1999-03-07, 百拇医药