试用灰关联分析法综合评估学生预防保健相关指标
作者:丁小兵
单位:丁小兵(江苏省大丰市卫生防疫站 大丰224100)
关键词:
数理医药学杂志000136
中图分类号:O 212.4
文章编号:1004-4337(2000)01-0063-02▲
学生预防保健相关指标主要有9大类[1]。客观准确地综合评估这些指标对全面衡量学校预防保健工作质量,指导卫生监督工作具有重要意义。目前对这9类指标的综合评估大多采用计分法,而计分法中确定每一指标所占的比分具有主观性。灰关联分析法具有评价范围广、无需权重系数、计算比较简单等优点,现已运用于医疗卫生等多个领域[2~4]。本文试用灰关联分析法对其进行综合评估以探索更为客观科学的评价方法。
, http://www.100md.com
1 资料来源
本文资料来源于大丰市1997年上半年8所学校五年级学生体检资料。体检人员为学校卫生专业人员和医务工作者,体检前经过专门培训。
2 计算方法与步骤
2.1 建立数据矩阵
根据问题的实质,有分析域S=(S1,S2,…,S8),Si分别代表8所学校。
收集体检原始数据,根据学校卫生情况年报表的有关要求,将每一学校原始体检数据除以每学校的体检人数(或牙数)得表1,为便于比较分析,身高、体重只取其中等和下等。
表1 大丰市某8所学校五年级学生预防保健指标基本数据(%) 指
, 百拇医药
标
身 高
体 重
营
养
不
良
肥
胖
视
力
不
良
恒牙龋患
, http://www.100md.com
沙 眼
贫 血
蛔 虫
中等
下等
中等
下等
龋
齿
数
活动龋牙数
龋
失
牙
, 百拇医药
数
已
补
牙
数
可
疑
沙
眼
沙
眼
矫
治
人
, 百拇医药
数
阳
性
人
数
治
疗
人
数
阳
性
人
数
投
, http://www.100md.com
药
人
数
代号
Xi1
Xi2
Xi3
Xi4
Xi5
Xi6
Xi7
Xi8
, http://www.100md.com
Xi9
Xi10
Xi11
Xi12
Xi13
Xi14
Xi15
Xi16
Xi17
Xi18
, http://www.100md.com
属性
↑
↓
↑
↓
↓
↓
↓
↓
↓
↓
↑
↓
↓
, http://www.100md.com
↑
↓
↑
↓
↑
S1
86.3
10.7
87.2
11.1
16.2
10.2
38.7
, http://www.100md.com
31.1
5.2
8.4
19.3
12.3
22.6
100
3.2
92.2
6.3
100
S2
92.1
, 百拇医药
2.1
94.2
4.4
4.2
12.3
60.1
38.4
6.3
10.1
80.2
8.2
10.2
100
, 百拇医药
1.7
100
2.3
100
S3
89.4
3.4
87.2
4.2
3.7
9.8
58.2
34.1
, http://www.100md.com
3.4
8.3
70.2
4.6
9.8
100
1.8
100
2.2
100
S4
85.4
10.8
, 百拇医药
82.3
10.8
14.7
11.1
32.3
31.2
5.4
8.5
9.3
11.2
23.1
100
2.8
, 百拇医药
80.1
5.8
100
S5
86.7
8.4
84.1
9.8
13.8
9.7
34.3
32.8
4.7
, 百拇医药
6.2
11.2
12.2
20.8
100
2.7
100
4.2
100
S6
84.6
8.7
86.3
, 百拇医药
10.2
12.4
10.2
28.7
22.7
7.1
6.3
10.8
13.1
21.3
100
2.8
100
, 百拇医药
5.2
100
S7
88.1
4.1
9.1
4.8
7.8
9.8
52.1
36.2
5.2
4.2
, 百拇医药
62.1
9.3
11.4
100
4.2
100
3.1
100
S8
89.4
6.2
86.2
8.2
, 百拇医药
11.2
10.7
48.6
32.8
8.6
7.4
66.3
12.2
14.8
100
3.9
100
3.1
, 百拇医药
100
基准列
92.1
2.1
94.2
4.2
3.7
9.7
28.7
22.7
3.4
4.2
80.2
, http://www.100md.com
4.6
9.8
100
1.7
100
2.2
100
注:↑表示指标值越大越好;↓表示指标值越小越好。
根据各特征指标的属性,对参于分析的表1数据作统一尺度和同一化处理。对指标属性越大越好的指标:
X′ij=Xij/max(Xij) i∈I
, http://www.100md.com
对指标属性越小越好的指标:
X′ij=min(Xij)/Xij i∈I
经上述处理,表1中的数据可转化为表2。
表2 分析体系数据 代号
Xi1
Xi2
Xi3
Xi4
Xi5
Xi6
, 百拇医药
Xi7
Xi8
Xi9
Xi10
Xi11
Xi12
Xi13
Xi14
Xi15
Xi16
, http://www.100md.com
Xi17
Xi18
属性
↑
↓
↑
↓
↑
↓
↓
↓
↓
↓
, 百拇医药
↑
↓
↑
↓
↓
↑
↓
↑
S1
0.9370
0.1963
0.9257
0.3784
, http://www.100md.com
0.2284
0.9510
0.7416
0.7299
0.6538
0.5000
0.2406
0.3739
0.4336
1
0.5313
0.922
0.3492
, 百拇医药
1
S2
1
1
1
0.9545
0.8809
0.7886
0.4775
0.5911
0.5397
0.4158
1
, http://www.100md.com
0.5610
0.9608
1
1
1
0.9565
1
S3
0.9707
0.6176
0.9257
1
1
, http://www.100md.com
0.9898
0.4931
0.6657
1
0.5060
0.8753
1
1
1
0.9444
1
1
1
, 百拇医药
S4
0.9273
0.1944
0.8907
0.3889
0.2517
0.8739
0.8885
0.7276
0.6296
0.4941
0.1159
, 百拇医药
0.4107
0.4242
1
0.6071
0.8010
0.3793
1
S5
0.9414
0.2500
0.8928
0.4285
, http://www.100md.com 0.2681
1
0.8367
0.6921
0.8293
0.6667
0.1347
0.3511
0.4601
1
0.6071
1
0.4231
, http://www.100md.com
1
S6
0.9121
0.2414
0.9161
0.4118
0.2984
0.9510
1
1
0.4788
0.6667
0.1347
, 百拇医药
0.3511
0.4601
1
0.6071
1
0.4231
1
S7
0.9567
0.5122
0.9565
0.8750
0.4743
, 百拇医药
0.9898
0.5509
0.6271
0.6538
1
0.7743
0.4946
0.9896
1
0.4047
1
0.4583
1
, http://www.100md.com
S8
0.9707
0.3387
0.9151
0.5122
0.3304
0.9065
0.5905
0.6921
0.3953
0.5675
0.8267
, http://www.100md.com
0.3770
0.6622
1
0.4359
1
0.7096
1
基准列
1
1
1
1
1
, http://www.100md.com 1
1
1
1
1
1
1
1
1
1
1
1
1
2.2 关联度的计算及关联序的确定
, 百拇医药
利用下列公式可计算关联系数ξi(k):
δ为分辩系数,可选0.5。
利用下列公式可求得关联度r: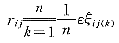
本例计算时,可将上述表2中的数据化为下列差矩阵。
如△11=|1-0.9370|=0.063,余类推
X1
X2
X3
, 百拇医药
X4
X5
X6
X7
X8
X9
X10
X11
X12
X13
X14
, http://www.100md.com
X15
X16
X17
X18
△1
0.063
0.803
0.074
0.622
0.772
0.049
0.258
, http://www.100md.com
0.270
0.346
0.50
0.759
0.626
0.566
0
0.469
0.078
0.660
0
△2
0
, 百拇医药
0
0
0.045
0.119
0.212
0.522
0.409
0.460
0.584
0
0.439
0.039
0
, 百拇医药
0
0
0.044
0
△3
0.029
0.382
0.074
0
0
0.010
0.507
0.334
, 百拇医药
0
0.494
0.124
0
0
0
0.056
0
0
0
△4
0.072
0.826
, 百拇医药
0.109
0.611
0.748
0.126
0.112
0.273
0.370
0.505
0.884
0.588
0.565
0
0.392
, 百拇医药
0.199
0.630
0
△5
0.058
0.75
0.107
0.572
0.732
0
0.163
0.307
0.170
, 百拇医药
0.323
0.860
0.622
0.528
0
0.371
0
0.477
0
△6
0.088
0.759
0.084
, 百拇医药
0.589
0.702
0.049
0
0
0.522
0.334
0.865
0.649
0.539
0
0.392
0
, 百拇医药
0.576
0
△7
0.043
0.488
0.043
0.125
0.526
0.010
0.449
0.372
0.346
0
, 百拇医药
0.226
0.606
0.011
0
0.696
0
0.542
0
△8
0.029
0.662
0.084
0.488
, 百拇医药
0.669
0.094
0.409
0.307
0.610
0.433
0.173
0.622
0.338
0
0.663
0
0.290
, http://www.100md.com
0
上述差矩阵中△max=0.884,△min=0.00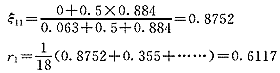
同理:r2=0.8108,r3=0.8434,r4=0.6288,r5=0.6489,r6=0.6666,r7=0.7231,r8=0.5979
根据关联度排序,8所学校我五年级学生预防保健指标综合评比由好向差的排序为:
S3>S2>S7>S6>S5>S4>S1>S8
, http://www.100md.com
3 讨论
3.1 本文试用灰关联分析法对我市8所学校五年级学生的预防保健相关指标进行了综合评价,得到8所学校学生的预防保健工作质量以学校3最好,其次是学校2,较差的是学校8和学校7。学校3和学校我2是两所城区中心小学,平时比较注重学生的预防保健,一些相关疾病发病率较低。而学校8和学校7是两所农村小学,平时不注重预防保健,学生常见病的发病率较高。本文运用的关联分析法的分析结果与实际情况基本一致。
3.2 灰关联分析是灰色系统中的分析方法之一,它能从各因素与系统的发展趋势的相似程度来衡量其关联水平,因此,不需要预先知道其数据分布,对样本量要求也不高。本文试用这一方法对学生预防保健进行综合分析,其计算比较简单,容易理解,有值得推广的价值。■
参考文献:
[1] 白呼群主编.学校卫生情况年报表技术规范.中国卫生监督统计报表第二版.北京:北京医科大学,中国协和医科大学联合出版社,1997,30.
[2] 马立军.关联分析在医学研究中的应用.中国卫生统计,1992,9(1):41.
[3] 洗必勋.灰色聚类法在医院工作质量综合评价中的应用.中国卫生统计,1997,9(5):8.
[4] 吴秉忠.灰色关联用于乙型肝炎感染水平地域性差异的分析.中国卫生统计,1996,13(5):42.
[5] 吴彬等.灰关联聚类法在医院工作质量评价中的应用.中国卫生统计,1997,14(3):17.
收稿日期:1999-02-18, 百拇医药
单位:丁小兵(江苏省大丰市卫生防疫站 大丰224100)
关键词:
数理医药学杂志000136
中图分类号:O 212.4
文章编号:1004-4337(2000)01-0063-02▲
学生预防保健相关指标主要有9大类[1]。客观准确地综合评估这些指标对全面衡量学校预防保健工作质量,指导卫生监督工作具有重要意义。目前对这9类指标的综合评估大多采用计分法,而计分法中确定每一指标所占的比分具有主观性。灰关联分析法具有评价范围广、无需权重系数、计算比较简单等优点,现已运用于医疗卫生等多个领域[2~4]。本文试用灰关联分析法对其进行综合评估以探索更为客观科学的评价方法。
, http://www.100md.com
1 资料来源
本文资料来源于大丰市1997年上半年8所学校五年级学生体检资料。体检人员为学校卫生专业人员和医务工作者,体检前经过专门培训。
2 计算方法与步骤
2.1 建立数据矩阵
根据问题的实质,有分析域S=(S1,S2,…,S8),Si分别代表8所学校。
收集体检原始数据,根据学校卫生情况年报表的有关要求,将每一学校原始体检数据除以每学校的体检人数(或牙数)得表1,为便于比较分析,身高、体重只取其中等和下等。
表1 大丰市某8所学校五年级学生预防保健指标基本数据(%) 指
, 百拇医药
标
身 高
体 重
营
养
不
良
肥
胖
视
力
不
良
恒牙龋患
, http://www.100md.com
沙 眼
贫 血
蛔 虫
中等
下等
中等
下等
龋
齿
数
活动龋牙数
龋
失
牙
, 百拇医药
数
已
补
牙
数
可
疑
沙
眼
沙
眼
矫
治
人
, 百拇医药
数
阳
性
人
数
治
疗
人
数
阳
性
人
数
投
, http://www.100md.com
药
人
数
代号
Xi1
Xi2
Xi3
Xi4
Xi5
Xi6
Xi7
Xi8
, http://www.100md.com
Xi9
Xi10
Xi11
Xi12
Xi13
Xi14
Xi15
Xi16
Xi17
Xi18
, http://www.100md.com
属性
↑
↓
↑
↓
↓
↓
↓
↓
↓
↓
↑
↓
↓
, http://www.100md.com
↑
↓
↑
↓
↑
S1
86.3
10.7
87.2
11.1
16.2
10.2
38.7
, http://www.100md.com
31.1
5.2
8.4
19.3
12.3
22.6
100
3.2
92.2
6.3
100
S2
92.1
, 百拇医药
2.1
94.2
4.4
4.2
12.3
60.1
38.4
6.3
10.1
80.2
8.2
10.2
100
, 百拇医药
1.7
100
2.3
100
S3
89.4
3.4
87.2
4.2
3.7
9.8
58.2
34.1
, http://www.100md.com
3.4
8.3
70.2
4.6
9.8
100
1.8
100
2.2
100
S4
85.4
10.8
, 百拇医药
82.3
10.8
14.7
11.1
32.3
31.2
5.4
8.5
9.3
11.2
23.1
100
2.8
, 百拇医药
80.1
5.8
100
S5
86.7
8.4
84.1
9.8
13.8
9.7
34.3
32.8
4.7
, 百拇医药
6.2
11.2
12.2
20.8
100
2.7
100
4.2
100
S6
84.6
8.7
86.3
, 百拇医药
10.2
12.4
10.2
28.7
22.7
7.1
6.3
10.8
13.1
21.3
100
2.8
100
, 百拇医药
5.2
100
S7
88.1
4.1
9.1
4.8
7.8
9.8
52.1
36.2
5.2
4.2
, 百拇医药
62.1
9.3
11.4
100
4.2
100
3.1
100
S8
89.4
6.2
86.2
8.2
, 百拇医药
11.2
10.7
48.6
32.8
8.6
7.4
66.3
12.2
14.8
100
3.9
100
3.1
, 百拇医药
100
基准列
92.1
2.1
94.2
4.2
3.7
9.7
28.7
22.7
3.4
4.2
80.2
, http://www.100md.com
4.6
9.8
100
1.7
100
2.2
100
注:↑表示指标值越大越好;↓表示指标值越小越好。
根据各特征指标的属性,对参于分析的表1数据作统一尺度和同一化处理。对指标属性越大越好的指标:
X′ij=Xij/max(Xij) i∈I
, http://www.100md.com
对指标属性越小越好的指标:
X′ij=min(Xij)/Xij i∈I
经上述处理,表1中的数据可转化为表2。
表2 分析体系数据 代号
Xi1
Xi2
Xi3
Xi4
Xi5
Xi6
, 百拇医药
Xi7
Xi8
Xi9
Xi10
Xi11
Xi12
Xi13
Xi14
Xi15
Xi16
, http://www.100md.com
Xi17
Xi18
属性
↑
↓
↑
↓
↑
↓
↓
↓
↓
↓
, 百拇医药
↑
↓
↑
↓
↓
↑
↓
↑
S1
0.9370
0.1963
0.9257
0.3784
, http://www.100md.com
0.2284
0.9510
0.7416
0.7299
0.6538
0.5000
0.2406
0.3739
0.4336
1
0.5313
0.922
0.3492
, 百拇医药
1
S2
1
1
1
0.9545
0.8809
0.7886
0.4775
0.5911
0.5397
0.4158
1
, http://www.100md.com
0.5610
0.9608
1
1
1
0.9565
1
S3
0.9707
0.6176
0.9257
1
1
, http://www.100md.com
0.9898
0.4931
0.6657
1
0.5060
0.8753
1
1
1
0.9444
1
1
1
, 百拇医药
S4
0.9273
0.1944
0.8907
0.3889
0.2517
0.8739
0.8885
0.7276
0.6296
0.4941
0.1159
, 百拇医药
0.4107
0.4242
1
0.6071
0.8010
0.3793
1
S5
0.9414
0.2500
0.8928
0.4285
, http://www.100md.com 0.2681
1
0.8367
0.6921
0.8293
0.6667
0.1347
0.3511
0.4601
1
0.6071
1
0.4231
, http://www.100md.com
1
S6
0.9121
0.2414
0.9161
0.4118
0.2984
0.9510
1
1
0.4788
0.6667
0.1347
, 百拇医药
0.3511
0.4601
1
0.6071
1
0.4231
1
S7
0.9567
0.5122
0.9565
0.8750
0.4743
, 百拇医药
0.9898
0.5509
0.6271
0.6538
1
0.7743
0.4946
0.9896
1
0.4047
1
0.4583
1
, http://www.100md.com
S8
0.9707
0.3387
0.9151
0.5122
0.3304
0.9065
0.5905
0.6921
0.3953
0.5675
0.8267
, http://www.100md.com
0.3770
0.6622
1
0.4359
1
0.7096
1
基准列
1
1
1
1
1
, http://www.100md.com 1
1
1
1
1
1
1
1
1
1
1
1
1
2.2 关联度的计算及关联序的确定
, 百拇医药
利用下列公式可计算关联系数ξi(k):

δ为分辩系数,可选0.5。
利用下列公式可求得关联度r:
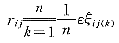
本例计算时,可将上述表2中的数据化为下列差矩阵。
如△11=|1-0.9370|=0.063,余类推
X1
X2
X3
, 百拇医药
X4
X5
X6
X7
X8
X9
X10
X11
X12
X13
X14
, http://www.100md.com
X15
X16
X17
X18
△1
0.063
0.803
0.074
0.622
0.772
0.049
0.258
, http://www.100md.com
0.270
0.346
0.50
0.759
0.626
0.566
0
0.469
0.078
0.660
0
△2
0
, 百拇医药
0
0
0.045
0.119
0.212
0.522
0.409
0.460
0.584
0
0.439
0.039
0
, 百拇医药
0
0
0.044
0
△3
0.029
0.382
0.074
0
0
0.010
0.507
0.334
, 百拇医药
0
0.494
0.124
0
0
0
0.056
0
0
0
△4
0.072
0.826
, 百拇医药
0.109
0.611
0.748
0.126
0.112
0.273
0.370
0.505
0.884
0.588
0.565
0
0.392
, 百拇医药
0.199
0.630
0
△5
0.058
0.75
0.107
0.572
0.732
0
0.163
0.307
0.170
, 百拇医药
0.323
0.860
0.622
0.528
0
0.371
0
0.477
0
△6
0.088
0.759
0.084
, 百拇医药
0.589
0.702
0.049
0
0
0.522
0.334
0.865
0.649
0.539
0
0.392
0
, 百拇医药
0.576
0
△7
0.043
0.488
0.043
0.125
0.526
0.010
0.449
0.372
0.346
0
, 百拇医药
0.226
0.606
0.011
0
0.696
0
0.542
0
△8
0.029
0.662
0.084
0.488
, 百拇医药
0.669
0.094
0.409
0.307
0.610
0.433
0.173
0.622
0.338
0
0.663
0
0.290
, http://www.100md.com
0
上述差矩阵中△max=0.884,△min=0.00
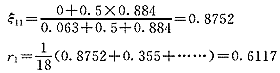
同理:r2=0.8108,r3=0.8434,r4=0.6288,r5=0.6489,r6=0.6666,r7=0.7231,r8=0.5979
根据关联度排序,8所学校我五年级学生预防保健指标综合评比由好向差的排序为:
S3>S2>S7>S6>S5>S4>S1>S8
, http://www.100md.com
3 讨论
3.1 本文试用灰关联分析法对我市8所学校五年级学生的预防保健相关指标进行了综合评价,得到8所学校学生的预防保健工作质量以学校3最好,其次是学校2,较差的是学校8和学校7。学校3和学校我2是两所城区中心小学,平时比较注重学生的预防保健,一些相关疾病发病率较低。而学校8和学校7是两所农村小学,平时不注重预防保健,学生常见病的发病率较高。本文运用的关联分析法的分析结果与实际情况基本一致。
3.2 灰关联分析是灰色系统中的分析方法之一,它能从各因素与系统的发展趋势的相似程度来衡量其关联水平,因此,不需要预先知道其数据分布,对样本量要求也不高。本文试用这一方法对学生预防保健进行综合分析,其计算比较简单,容易理解,有值得推广的价值。■
参考文献:
[1] 白呼群主编.学校卫生情况年报表技术规范.中国卫生监督统计报表第二版.北京:北京医科大学,中国协和医科大学联合出版社,1997,30.
[2] 马立军.关联分析在医学研究中的应用.中国卫生统计,1992,9(1):41.
[3] 洗必勋.灰色聚类法在医院工作质量综合评价中的应用.中国卫生统计,1997,9(5):8.
[4] 吴秉忠.灰色关联用于乙型肝炎感染水平地域性差异的分析.中国卫生统计,1996,13(5):42.
[5] 吴彬等.灰关联聚类法在医院工作质量评价中的应用.中国卫生统计,1997,14(3):17.
收稿日期:1999-02-18, 百拇医药