细菌性痢疾季节性分布数学模型
作者：李雄
单位：李雄(湖北医科大学医疗系97级研究生 武汉430071)
关键词：细菌性痢疾；季节性分布；数学模型
数理医药学杂志000304
摘 要 试用Logistic模型：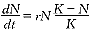
模拟细菌性痢疾季节性分布，并讨论了模型中参数K和r的流行病学意义。
中图分类号：R 516.4 文献标识码：A
文章编号：1004-4337(2000)03-0199-01
细菌性痢疾作为一种常见传染性疾病，在其发病的季节性分布方面已积累了大量数据，已有文献对此作了数据统计，如文献[1]用圆形分布构成比法[2，3]分析了山东泰安市1991～1995年细菌性痢疾发病季节性特征，得出了一些有意义的结果，但此法在揭示该病的动态性变化过程方面尚嫌不足，因此，我们在此应用Logistic模型，拟从动态角度揭示细菌性痢疾发病率逐月变化过程。
, 百拇医药
本文试用泰安市1991年男性细菌性痢疾患者数据[1]作为取材、分析及模型化对象，原始实测数据见表1(为了有利于疫情保密，原文已将发病的数据转换成构成比)。
表1 原始痢疾发病率(N1)、原始痢疾累计发病率(N2)、模型痢疾累计发病率(N3)三者逐月(t)变化情况 t
2
3
4
5
6
7
8
, 百拇医药
9
10
11
12
N1
0.00220
0.00936
0.01487
0.02423
0.05121
0.19548
0.26707
, 百拇医药 0.22302
0.14868
0.04681
0.00826
N2
0.00220
0.01156
0.02643
0.05066
0.10187
0.29735
0.56442
, 百拇医药
0.78744
0.93612
0.98293
0.99119
N3
0.00287
0.00787
0.02136
0.05672
0.14221
0.31435
0.56001
, 百拇医药
0.78223
0.91410
0.97364
0.99723
我们试用Logistic方程[4]来模拟细菌性痢疾发病率逐月变化过程。Logistic方程为：
(1)
其中，N为细菌性痢疾累计发病率，t为月份(月)。为了便于模型化，令N|t=2=N0
r>0,K>N>0
方程(1)的解为：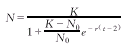
(2)
, 百拇医药
下面确定(1)、(2)两式中参数K、r、N0的值。
根据四点式平均值估计法[5]，可算得K=1.0112
(2)式等价于：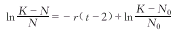
(3)
令
于是(3)变为：
y=A+Bx
利用最小二乘法可计算出
N0=0.00287, r=1.0131
, 百拇医药
于是(1)式及(2)式分别变成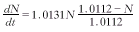
(4)
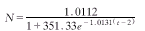(5)
(4)、(5)两式即分别为细菌性痢疾季节性分布模型及模型的解。
Logistic模型除了可用于描述生态学上的种群生长外，还可较好地描述细菌性痢疾累计发病率逐月增长而变化的过程。
模型中参数K、r在生态学中分别指“环境容纳量”和“内秉增长率”，在流行病学中不妨称之为“痢疾最大发病率”和“痢疾内秉增加率”。
参考文献
1，李应光等.细菌性痢疾发病季节特征统计分析.中国医院统计，1997，4(1)：18～19.
2，金丕焕主编.医用统计方法.上海：上海医科大学出版社，1993，210～214.
3，阙少聪等.圆形分布构成比法计算疾病季节高峰月日的探讨.中国公共卫生，1994，10(5)：217～219.
4，陈兰荪.数学生态学模型与理论方法.北京：科学出版社，1988.
5，王振中等.逻辑斯谛曲线K值的四点式平均值估计法.生态学报，1987，7(3)：193～197.
收稿日期：1999-11-23, 百拇医药
单位：李雄(湖北医科大学医疗系97级研究生 武汉430071)
关键词：细菌性痢疾；季节性分布；数学模型
数理医药学杂志000304
摘 要 试用Logistic模型：
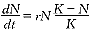模拟细菌性痢疾季节性分布，并讨论了模型中参数K和r的流行病学意义。中图分类号：R 516.4 文献标识码：A
文章编号：1004-4337(2000)03-0199-01
细菌性痢疾作为一种常见传染性疾病，在其发病的季节性分布方面已积累了大量数据，已有文献对此作了数据统计，如文献[1]用圆形分布构成比法[2，3]分析了山东泰安市1991～1995年细菌性痢疾发病季节性特征，得出了一些有意义的结果，但此法在揭示该病的动态性变化过程方面尚嫌不足，因此，我们在此应用Logistic模型，拟从动态角度揭示细菌性痢疾发病率逐月变化过程。
, 百拇医药
本文试用泰安市1991年男性细菌性痢疾患者数据[1]作为取材、分析及模型化对象，原始实测数据见表1(为了有利于疫情保密，原文已将发病的数据转换成构成比)。
表1 原始痢疾发病率(N1)、原始痢疾累计发病率(N2)、模型痢疾累计发病率(N3)三者逐月(t)变化情况 t
2
3
4
5
6
7
8
, 百拇医药
9
10
11
12
N1
0.00220
0.00936
0.01487
0.02423
0.05121
0.19548
0.26707
, 百拇医药 0.22302
0.14868
0.04681
0.00826
N2
0.00220
0.01156
0.02643
0.05066
0.10187
0.29735
0.56442
, 百拇医药
0.78744
0.93612
0.98293
0.99119
N3
0.00287
0.00787
0.02136
0.05672
0.14221
0.31435
0.56001
, 百拇医药
0.78223
0.91410
0.97364
0.99723
我们试用Logistic方程[4]来模拟细菌性痢疾发病率逐月变化过程。Logistic方程为：
(1)其中，N为细菌性痢疾累计发病率，t为月份(月)。为了便于模型化，令N|t=2=N0
r>0,K>N>0
方程(1)的解为：
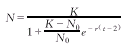(2), 百拇医药
下面确定(1)、(2)两式中参数K、r、N0的值。
根据四点式平均值估计法[5]，可算得K=1.0112
(2)式等价于：
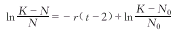(3)令
于是(3)变为：
y=A+Bx
利用最小二乘法可计算出
N0=0.00287, r=1.0131
, 百拇医药
于是(1)式及(2)式分别变成
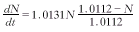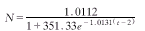(4) (5)(4)、(5)两式即分别为细菌性痢疾季节性分布模型及模型的解。
Logistic模型除了可用于描述生态学上的种群生长外，还可较好地描述细菌性痢疾累计发病率逐月增长而变化的过程。
模型中参数K、r在生态学中分别指“环境容纳量”和“内秉增长率”，在流行病学中不妨称之为“痢疾最大发病率”和“痢疾内秉增加率”。
参考文献
1，李应光等.细菌性痢疾发病季节特征统计分析.中国医院统计，1997，4(1)：18～19.
2，金丕焕主编.医用统计方法.上海：上海医科大学出版社，1993，210～214.
3，阙少聪等.圆形分布构成比法计算疾病季节高峰月日的探讨.中国公共卫生，1994，10(5)：217～219.
4，陈兰荪.数学生态学模型与理论方法.北京：科学出版社，1988.
5，王振中等.逻辑斯谛曲线K值的四点式平均值估计法.生态学报，1987，7(3)：193～197.
收稿日期：1999-11-23, 百拇医药