放射性链递次衰变微分方程组的通解的递推公式
作者:张岱
单位:张岱(锦州医学院 锦州121001)
关键词:放射性衰变;微分方程组;代数解法
数理医药学杂志000303
摘 要 用代数方法给出了放射性链递次衰变微分方程组解的递推公式。该递推公式既可以用电子计算机计算任何一代子核的衰变规律,也可以用递推公式给出的法则直接写出任何一代子核的衰变规律。
中图分类号:O 241.8 文献标识码:A
文章编号:1004-4337(2000)03-0197-02
1 引言
依放射性原子核递次衰变的物理模型所建立的微分方程组,由于未知函数数目庞大,互相关联,许多文献的成功解法虽各有千秋,但在数学处理过程中都难免冗长、计算繁琐[1~5]。本文用代数方法给出微分方程组解的递推公式,既可以用电子计算机计算,也可以由递推公式给出法则直接写出任何一代子核的衰变规律。本文先给出递推公式,然后叙述如何由递推公式的规律直接写出任何一代子核的衰变解。
, 百拇医药
2 多分支链放射核递次衰变的微分方程组
如果考虑到衰变链上任意一代子核都是其后代子核的母核,则放射性核的衰变将是一条具有多分支的递次衰变的链[6]。即:
与此多分支递次衰变链相应的微分方程组为: (1)
(1)
式中,Ni为t时刻的第i代子核数;λj为第j代子核的衰变常数;bij≥0(i>j,且i≥j+3时为0)为第j代子核衰变向第i代子核的传递系数,它等于λj乘以第j代子核向第i代子核衰变的分支比。
3 微分方程组解的传递公式
, http://www.100md.com
由常微分方程的理论可知[7],常微分方程组(2)的解组为一系列指数e-λjt型的和式,因此设各代子核的衰变解如下: (2)
(2)
式中,Aij为待定常数,其中Aii型待定常数由初始条件来确定。为此,在(2)式中,设t=0,则由第i代子核Ni(t)的表达式可得下列递推公式: (3)
(3)
式中,Ni(0)为第i代放射性衰变,t=0时的初始子核数。由(3)式可见,尚需确定常数Aij(i>j),才可最终求得Aii。为此,必须将(2)式的前i个解式代入(1)式中的第i式,则有: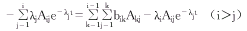 (4)
(4)
, http://www.100md.com
比较(4)式两边e-λjt的系数,则得下列递推公式: (5)
(5)
将(5)式代入(3)式得: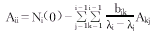 (6)
(6)
将(3)式和(6)式代入(2)式得: (7)
(7)
上述第(7)式即所求的放射性核递次衰变微分方程组(1)的通解表达式。
4 由通解公式(7)直接写出任意代子核的衰变解
表面看来,这个通解表达式比文献[3]的通解表达式更繁琐冗长,但仔细考察(3)式和(5)式可得一个简单的法则,据此,不须任何计算便可写出微分方程组(1)的任何一代子核的衰变解。可见,只要找出待定常数Aij的规则,便可写出解来,其方法如下:
, http://www.100md.com
1 首先写出由i到j(i>j)连续正整数;
2 写出首数i,尾数j的合部两数组、三数组…;
3 将多于三个数组,分解成首数第二数、第二第三数、第三第四数的数组,这些数组就是b因子的双下标,而这些b因子的乘积就是Aij项的分子;
4 取上述相应数组为λ的下标,每个下标大的λ都与有最小下标的λ相减,这些差因子的乘积就是相同该数组对应项的分母;
5 写出Aii后,再由(6)式求出Aij。有了Aii和Aij就可以写出任何一代子核的衰变解。
应用举例
① 因为i=2,j=1,只有首为2尾为1的二数组合2 1一个,故 (7)
(7)
, http://www.100md.com
② 设i=3,j=1,共有两个数组合3 1和3 2 1,故 (8)
(8)
而i=3,j=2,只有一个数组3 2,故 (9)
(9)
由(3)式,有 (10)
(10)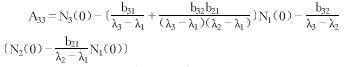 (11)
(11)
③ 设i=4,j=1,共有数组四个,为
故
, http://www.100md.com
而i=4,j=2,数组为4 2和4 3 2,故 (12)
(12)
可知数组4 3的对应项为: (13)
(13)
由(7)式和(2)式有: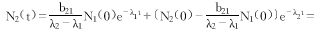 (14)
(14)
由(8)~(11)式和(2)式有:

 (15)
(15)
, 百拇医药
可见本文的(14)式和(15)式与文献[6]的(3)式所给出的结果完全相同。须知文献[6]的N1(t)、N2(t)、N3(t)和N4(t)并不是最终结果,欲求最终表达式还需经过若干次代换的运算,而本文的(14)式和(15)式是不需计算直接写出。为节省篇幅本文未写出N4(t)的表达式,可以确信,它也和文献[6]N4(t)的结果一致。
5 结束语
本文从线性常微分方程组理论出发,用试探解的方法,十分简便地给出了放射核多分支链微分方程解的递推公式。该通解表达式,还蕴涵着一个简便的规律。因此当子核代数太大时,可以上机运算,推出任何一代子核的衰变规律;而当子核代数不太大时,即可以递推公式(7)算出,还可以用下标规律方法不用任何运算,直接写出任何一代子核的衰变律。这是以前任何文献未曾给出的。
, 百拇医药
参考文献
1,赵英荣,放射系中各元素原子核的计算.大学物理,1988,7(5):6.
2,谷震槐.用拉普拉斯变换求放射性原子核递次衰变的规律.大学物理,1992,11(10):35.
3,陈玉珂.放射性核递次衰变规律的普适解.大学物理,1993,12(12):22.
4,卢希庭.原子核物理.北京:原子能出版社,1981.
5,P.A詹森〔美〕,孙东川译.网络流规划.北京:科学出版社,1988.
6,王蔚东.放射性递次衰变方程的E因子解法.大学物理,1996,15(8):16.
7,数学手册,北京:人民教育出版社,1979,660~662.
收稿日期:1999-09-06, 百拇医药
单位:张岱(锦州医学院 锦州121001)
关键词:放射性衰变;微分方程组;代数解法
数理医药学杂志000303
摘 要 用代数方法给出了放射性链递次衰变微分方程组解的递推公式。该递推公式既可以用电子计算机计算任何一代子核的衰变规律,也可以用递推公式给出的法则直接写出任何一代子核的衰变规律。
中图分类号:O 241.8 文献标识码:A
文章编号:1004-4337(2000)03-0197-02
1 引言
依放射性原子核递次衰变的物理模型所建立的微分方程组,由于未知函数数目庞大,互相关联,许多文献的成功解法虽各有千秋,但在数学处理过程中都难免冗长、计算繁琐[1~5]。本文用代数方法给出微分方程组解的递推公式,既可以用电子计算机计算,也可以由递推公式给出法则直接写出任何一代子核的衰变规律。本文先给出递推公式,然后叙述如何由递推公式的规律直接写出任何一代子核的衰变解。
, 百拇医药
2 多分支链放射核递次衰变的微分方程组
如果考虑到衰变链上任意一代子核都是其后代子核的母核,则放射性核的衰变将是一条具有多分支的递次衰变的链[6]。即:

与此多分支递次衰变链相应的微分方程组为:
 (1)
(1)式中,Ni为t时刻的第i代子核数;λj为第j代子核的衰变常数;bij≥0(i>j,且i≥j+3时为0)为第j代子核衰变向第i代子核的传递系数,它等于λj乘以第j代子核向第i代子核衰变的分支比。
3 微分方程组解的传递公式
, http://www.100md.com
由常微分方程的理论可知[7],常微分方程组(2)的解组为一系列指数e-λjt型的和式,因此设各代子核的衰变解如下:
 (2)
(2)式中,Aij为待定常数,其中Aii型待定常数由初始条件来确定。为此,在(2)式中,设t=0,则由第i代子核Ni(t)的表达式可得下列递推公式:
 (3)
(3)式中,Ni(0)为第i代放射性衰变,t=0时的初始子核数。由(3)式可见,尚需确定常数Aij(i>j),才可最终求得Aii。为此,必须将(2)式的前i个解式代入(1)式中的第i式,则有:
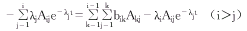 (4)
(4), http://www.100md.com
比较(4)式两边e-λjt的系数,则得下列递推公式:
 (5)
(5)将(5)式代入(3)式得:
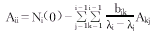 (6)
(6)将(3)式和(6)式代入(2)式得:
 (7)
(7)上述第(7)式即所求的放射性核递次衰变微分方程组(1)的通解表达式。
4 由通解公式(7)直接写出任意代子核的衰变解
表面看来,这个通解表达式比文献[3]的通解表达式更繁琐冗长,但仔细考察(3)式和(5)式可得一个简单的法则,据此,不须任何计算便可写出微分方程组(1)的任何一代子核的衰变解。可见,只要找出待定常数Aij的规则,便可写出解来,其方法如下:
, http://www.100md.com
1 首先写出由i到j(i>j)连续正整数;
2 写出首数i,尾数j的合部两数组、三数组…;
3 将多于三个数组,分解成首数第二数、第二第三数、第三第四数的数组,这些数组就是b因子的双下标,而这些b因子的乘积就是Aij项的分子;
4 取上述相应数组为λ的下标,每个下标大的λ都与有最小下标的λ相减,这些差因子的乘积就是相同该数组对应项的分母;
5 写出Aii后,再由(6)式求出Aij。有了Aii和Aij就可以写出任何一代子核的衰变解。
应用举例
① 因为i=2,j=1,只有首为2尾为1的二数组合2 1一个,故
 (7)
(7), http://www.100md.com
② 设i=3,j=1,共有两个数组合3 1和3 2 1,故
 (8)
(8)而i=3,j=2,只有一个数组3 2,故
 (9)
(9)由(3)式,有
 (10)
(10)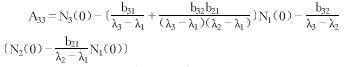 (11)
(11)③ 设i=4,j=1,共有数组四个,为

故

, http://www.100md.com
而i=4,j=2,数组为4 2和4 3 2,故
 (12)
(12)可知数组4 3的对应项为:
 (13)
(13)由(7)式和(2)式有:
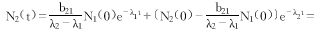 (14)
(14)由(8)~(11)式和(2)式有:


 (15)
(15), 百拇医药
可见本文的(14)式和(15)式与文献[6]的(3)式所给出的结果完全相同。须知文献[6]的N1(t)、N2(t)、N3(t)和N4(t)并不是最终结果,欲求最终表达式还需经过若干次代换的运算,而本文的(14)式和(15)式是不需计算直接写出。为节省篇幅本文未写出N4(t)的表达式,可以确信,它也和文献[6]N4(t)的结果一致。
5 结束语
本文从线性常微分方程组理论出发,用试探解的方法,十分简便地给出了放射核多分支链微分方程解的递推公式。该通解表达式,还蕴涵着一个简便的规律。因此当子核代数太大时,可以上机运算,推出任何一代子核的衰变规律;而当子核代数不太大时,即可以递推公式(7)算出,还可以用下标规律方法不用任何运算,直接写出任何一代子核的衰变律。这是以前任何文献未曾给出的。
, 百拇医药
参考文献
1,赵英荣,放射系中各元素原子核的计算.大学物理,1988,7(5):6.
2,谷震槐.用拉普拉斯变换求放射性原子核递次衰变的规律.大学物理,1992,11(10):35.
3,陈玉珂.放射性核递次衰变规律的普适解.大学物理,1993,12(12):22.
4,卢希庭.原子核物理.北京:原子能出版社,1981.
5,P.A詹森〔美〕,孙东川译.网络流规划.北京:科学出版社,1988.
6,王蔚东.放射性递次衰变方程的E因子解法.大学物理,1996,15(8):16.
7,数学手册,北京:人民教育出版社,1979,660~662.
收稿日期:1999-09-06, 百拇医药