纵向生命质量资料处理的伪多变量方差分析及轮廓分析法
作者:万崇华 方积乾 陈丽影 何磊 张玉祖 王之云
单位:万崇华(昆明医学院卫生统计学教研室 昆明650031);方积乾(中山医科大学卫生统计学教研室);陈丽影(云南省公安高等专科学校);何磊(云南省文山州妇幼保健院);张玉祖(昆明市戒毒所);王之云(昆明市戒毒所)
关键词:生命质量;吸毒;多变量方差分析;轮廓分析
数理医药学杂志000310
摘 要 介绍了用多元方差分析和轮廓分析思想来处理纵向生命质量资料的方法,并对有关的问题进行讨论。用这两种方法分析两戒毒组纵向测定的生命质量资料,结果表明两戒毒组的总生命质量在时间上的变动趋势无统计学显著性,但不同时点的测定值不同。
中图分类号:O 212.4 文献标识码:A
, http://www.100md.com
文章编号:1004-4337(2000)03-0208-02
随着生命质量(quality oflife,QOL)研究的兴起,涌现了大量的生命质量资料。由于生命质量的时间依赖性,必须进行纵向的重复多次的生命质量测定。但纵向测定资料的处理方法可以说还未很好解决,或者不太严谨或者理论太难而不易实行[1,2]。这严重阻碍着纵向生命质量测评的开展。本文将多元方差分析和轮廓分析引入纵向的生命质量分析中,并对有关的问题进行探讨。同时,对两组不同的吸毒者在戒毒期间生命质量的变化进行比较。
1 方法
1.1 伪多变量方差分析
众所周知,多变量方差分析[3]是同时对多个变量进行的方差分析,以推断不同组间的均向量有无不同。在纵向重复测量中,若把同一变量各时点的测定值作为不同的变量来处理,即可借用多变量方差分析来处理重复测量资料。为了与真正的多变量情形相区别,不妨称为伪多变量方差分析(quasi-MANOVA)。
, 百拇医药
显然,该法的优点是不必考虑不同时点间的相关问题,而整个作为一个整体来比较,而且可借用现成的多元方差分析法处理。缺点是只能得出处理组间比较的结果,而无法得到不同时点以及交互作用的结果。
1.2 轮廓分析
轮廓分析是分析多个变量间的轮廓(按一定顺序连接各变量间均值得到的折线)的一种多元统计方法[4]。显然,如按时间顺序连接某变量各时点测定值的均值,得到的轮廓即反映该变量在时间上的纵向变化规律。借用轮廓分析即可比较不同组间的变动规律是否一致。
实际上,轮郭分析是多变量方差分析的进一步推广,它把均向量比较的问题分析为如下三个具体的问题,从而可从不同角度获取更多信息。
① 各组的轮廓平行吗?
② 若平行,它们完全重合吗?
, http://www.100md.com
③ 若重合,它们的轮廓是水平的吗?
下面我们以两组比较为例,说明解决上述三个问题的方法。多组比较的以此相似,有兴趣者可参阅有关文献。
1.2.1 两总体轮郭平行的检验
两总体的轮郭平行,即两组间各时点的均值之差相同,若用μ1i,μ2i分别表示第一和第二组第i个时点的测定值均值,则等价于检验:
H0∶μ1,i-μ1,i-1=μ2,i-μ2,i-1,i=2,3…q
用矩阵式可写为:H0∶Cμ1=Cμ2,其中C为对照阵: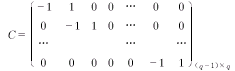
, 百拇医药
上述检验实际上是对用C变换后的数据的两组均向量比较,类似Hotelling T2检验可得到: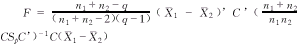
F满足于自由度为q-1,n1+n2-q的F分析。
1.2.2 两总体轮廓重合的检验
当两总体轮廓平行时,检验其重合等价于两均向量相等的检验,可直接用Hotelling T2检验。另外,也等价于检验:
H0∶μ11+μ12+…+μ1q=μ21+μ22+…+μ2q
, 百拇医药
令J为由q个1构成的列向量,则有: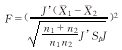
F满足于自由度为1,n1+n2-2的F分布。
1.2.3 两总体轮廓水平的检验
若两总体重合,可以用两样本数据计算合并的共同均向量,检验其是否水平,即检验各时点的均值是否相同。显然,若相同,则在时间上的变动即为一条水平的直线。这时,零假设可写为:
H0∶C(μ1+μ2)=0
相应的检验统计量为: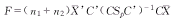
, http://www.100md.com
F满足于自由度为q-1,n1+n2-q的F分布。
2 实例分析
为了对不同的戒毒方式和方法的效果进行综合评价,我们以综合反映吸毒者的躯体、心理、社会功能以及戒断症状的生命质量为指标,用我们研制的吸毒者生命质量测定量表QOL-DA[5],在昆明市戒毒所随机抽取158例强制戒毒者和54例自愿戒毒者进行了五次纵向的生命质量测定。其各个时点的总生命质量得分及两组的比较结果见表1。
表1 两戒毒组不同时点的总生命质量
时间
强制组
自愿组
组间检验结果
, http://www.100md.com
例数
均数
标准差
例数
均数
标准差
t
p
戒毒前
158
114.71
32.41
54
, http://www.100md.com 118.61
31.51
-0.77
0.443
戒毒一周
153
123.06
37.08
54
126.43
32.55
-0.59
0.555
, http://www.100md.com
戒毒二周
135
139.56
33.81
46
140.61
33.09
-0.18
0.855
戒毒三周
124
154.39
29.98
, http://www.100md.com
37
154.73
27.88
-0.06
0.952
戒毒四周
122
164.61
26.12
32
169.53
21.92
-0.98
, 百拇医药
0.330
显然,割裂为多时点的分别比较存在两个主要缺陷:一是缺乏对总的变动趋势的检验,而且当各时点的检验结果不一致时难以下综合结论;二是多次重复检验增大一型错误的概率。为此,我们采用本文方法对两组总的变动趋势进行检验。
用1法得到:F=0.3468,P=0.8837。由此可认为两戒毒组的总生命质量在时间上的变动趋势相同。
用2法得到:
平均检验:F=0.3658,P=0.8326
重合检验:F=0.1372,P=0.7116
水平检验:F=324.68,P=0.0000
因为平等检验的P较大,可认为两轮廓平等。重合检验的P也很大,可认为重合。但水平检验P非常小,故认为不水平。至此,可认为两戒毒组的总生命质量变动模式相同,但不同时点上的值不一样。3 讨论
, 百拇医药
本文的两种方法原来都是用于具有多个指标的组间比较,这里借用来处理同一变量的多个时点数据。形式上相同,但本质不一样。
伪多变量方差分析和轮廓分析将纵向变化作为一个整体、作为一个总过程来处理,而不分析各测定点间的相互关系,从而不用考虑自相关问题,而且可借用已有的方法来处理纵向资料。
轮廓分析是多元方差分析的发展,两者的适用条件是相同的,均要求满足多元正态性和协方差阵齐性。
轮廓分析要按上述三个问题顺序进行。若前面的问题被拒绝了,就没有必要再进行后面的检验。
检验轮廓是否水平的方法显然也可分别用于各处理组比较其不同时点的均值是否相同,只要将其中相应的均向量和协差阵替换即可。这可作为经过伪多变量方差分析或轮廓分析有组间差异的不同组的补充检验,以便进一步说明各组不同时点上的均值是否一致。轮廓分析的计算主要是一些矩阵运算,我们用SAS的IML模块编制了其运算程序。
, http://www.100md.com
高等学校博士点学科专项科研基金资助
参考文献
1,Finiey DJ.Repeated measurements: what is measured and what repeats? Statist Med 1990,9:639.
2,Armitage P, Berry G. Statistical methods in medical research. Oxford: Elickwell Scientific Publications, 1987,354~357.
3,方开泰编著.实用多元统计分析.上海:华东师范大学出版社,1989:132~136.
4,王学仁,王松桂编译.实用多元统计分析.上海:上海科学技术出版社,1990,177~182.
5,万崇华,方积乾,陈丽影,等.海洛因成瘾者生存质量测定量表的制定及其考评.中国行为医学科学杂志,1997,6(3):169.
收稿日期:1999-10-05, 百拇医药
单位:万崇华(昆明医学院卫生统计学教研室 昆明650031);方积乾(中山医科大学卫生统计学教研室);陈丽影(云南省公安高等专科学校);何磊(云南省文山州妇幼保健院);张玉祖(昆明市戒毒所);王之云(昆明市戒毒所)
关键词:生命质量;吸毒;多变量方差分析;轮廓分析
数理医药学杂志000310
摘 要 介绍了用多元方差分析和轮廓分析思想来处理纵向生命质量资料的方法,并对有关的问题进行讨论。用这两种方法分析两戒毒组纵向测定的生命质量资料,结果表明两戒毒组的总生命质量在时间上的变动趋势无统计学显著性,但不同时点的测定值不同。
中图分类号:O 212.4 文献标识码:A
, http://www.100md.com
文章编号:1004-4337(2000)03-0208-02
随着生命质量(quality oflife,QOL)研究的兴起,涌现了大量的生命质量资料。由于生命质量的时间依赖性,必须进行纵向的重复多次的生命质量测定。但纵向测定资料的处理方法可以说还未很好解决,或者不太严谨或者理论太难而不易实行[1,2]。这严重阻碍着纵向生命质量测评的开展。本文将多元方差分析和轮廓分析引入纵向的生命质量分析中,并对有关的问题进行探讨。同时,对两组不同的吸毒者在戒毒期间生命质量的变化进行比较。
1 方法
1.1 伪多变量方差分析
众所周知,多变量方差分析[3]是同时对多个变量进行的方差分析,以推断不同组间的均向量有无不同。在纵向重复测量中,若把同一变量各时点的测定值作为不同的变量来处理,即可借用多变量方差分析来处理重复测量资料。为了与真正的多变量情形相区别,不妨称为伪多变量方差分析(quasi-MANOVA)。
, 百拇医药
显然,该法的优点是不必考虑不同时点间的相关问题,而整个作为一个整体来比较,而且可借用现成的多元方差分析法处理。缺点是只能得出处理组间比较的结果,而无法得到不同时点以及交互作用的结果。
1.2 轮廓分析
轮廓分析是分析多个变量间的轮廓(按一定顺序连接各变量间均值得到的折线)的一种多元统计方法[4]。显然,如按时间顺序连接某变量各时点测定值的均值,得到的轮廓即反映该变量在时间上的纵向变化规律。借用轮廓分析即可比较不同组间的变动规律是否一致。
实际上,轮郭分析是多变量方差分析的进一步推广,它把均向量比较的问题分析为如下三个具体的问题,从而可从不同角度获取更多信息。
① 各组的轮廓平行吗?
② 若平行,它们完全重合吗?
, http://www.100md.com
③ 若重合,它们的轮廓是水平的吗?
下面我们以两组比较为例,说明解决上述三个问题的方法。多组比较的以此相似,有兴趣者可参阅有关文献。
1.2.1 两总体轮郭平行的检验
两总体的轮郭平行,即两组间各时点的均值之差相同,若用μ1i,μ2i分别表示第一和第二组第i个时点的测定值均值,则等价于检验:
H0∶μ1,i-μ1,i-1=μ2,i-μ2,i-1,i=2,3…q
用矩阵式可写为:H0∶Cμ1=Cμ2,其中C为对照阵:
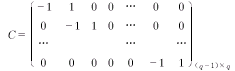
, 百拇医药
上述检验实际上是对用C变换后的数据的两组均向量比较,类似Hotelling T2检验可得到:
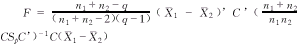
F满足于自由度为q-1,n1+n2-q的F分析。
1.2.2 两总体轮廓重合的检验
当两总体轮廓平行时,检验其重合等价于两均向量相等的检验,可直接用Hotelling T2检验。另外,也等价于检验:
H0∶μ11+μ12+…+μ1q=μ21+μ22+…+μ2q
, 百拇医药
令J为由q个1构成的列向量,则有:
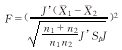
F满足于自由度为1,n1+n2-2的F分布。
1.2.3 两总体轮廓水平的检验
若两总体重合,可以用两样本数据计算合并的共同均向量,检验其是否水平,即检验各时点的均值是否相同。显然,若相同,则在时间上的变动即为一条水平的直线。这时,零假设可写为:
H0∶C(μ1+μ2)=0
相应的检验统计量为:
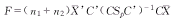
, http://www.100md.com
F满足于自由度为q-1,n1+n2-q的F分布。
2 实例分析
为了对不同的戒毒方式和方法的效果进行综合评价,我们以综合反映吸毒者的躯体、心理、社会功能以及戒断症状的生命质量为指标,用我们研制的吸毒者生命质量测定量表QOL-DA[5],在昆明市戒毒所随机抽取158例强制戒毒者和54例自愿戒毒者进行了五次纵向的生命质量测定。其各个时点的总生命质量得分及两组的比较结果见表1。
表1 两戒毒组不同时点的总生命质量
时间
强制组
自愿组
组间检验结果
, http://www.100md.com
例数
均数
标准差
例数
均数
标准差
t
p
戒毒前
158
114.71
32.41
54
, http://www.100md.com 118.61
31.51
-0.77
0.443
戒毒一周
153
123.06
37.08
54
126.43
32.55
-0.59
0.555
, http://www.100md.com
戒毒二周
135
139.56
33.81
46
140.61
33.09
-0.18
0.855
戒毒三周
124
154.39
29.98
, http://www.100md.com
37
154.73
27.88
-0.06
0.952
戒毒四周
122
164.61
26.12
32
169.53
21.92
-0.98
, 百拇医药
0.330
显然,割裂为多时点的分别比较存在两个主要缺陷:一是缺乏对总的变动趋势的检验,而且当各时点的检验结果不一致时难以下综合结论;二是多次重复检验增大一型错误的概率。为此,我们采用本文方法对两组总的变动趋势进行检验。
用1法得到:F=0.3468,P=0.8837。由此可认为两戒毒组的总生命质量在时间上的变动趋势相同。
用2法得到:
平均检验:F=0.3658,P=0.8326
重合检验:F=0.1372,P=0.7116
水平检验:F=324.68,P=0.0000
因为平等检验的P较大,可认为两轮廓平等。重合检验的P也很大,可认为重合。但水平检验P非常小,故认为不水平。至此,可认为两戒毒组的总生命质量变动模式相同,但不同时点上的值不一样。3 讨论
, 百拇医药
本文的两种方法原来都是用于具有多个指标的组间比较,这里借用来处理同一变量的多个时点数据。形式上相同,但本质不一样。
伪多变量方差分析和轮廓分析将纵向变化作为一个整体、作为一个总过程来处理,而不分析各测定点间的相互关系,从而不用考虑自相关问题,而且可借用已有的方法来处理纵向资料。
轮廓分析是多元方差分析的发展,两者的适用条件是相同的,均要求满足多元正态性和协方差阵齐性。
轮廓分析要按上述三个问题顺序进行。若前面的问题被拒绝了,就没有必要再进行后面的检验。
检验轮廓是否水平的方法显然也可分别用于各处理组比较其不同时点的均值是否相同,只要将其中相应的均向量和协差阵替换即可。这可作为经过伪多变量方差分析或轮廓分析有组间差异的不同组的补充检验,以便进一步说明各组不同时点上的均值是否一致。轮廓分析的计算主要是一些矩阵运算,我们用SAS的IML模块编制了其运算程序。
, http://www.100md.com
高等学校博士点学科专项科研基金资助
参考文献
1,Finiey DJ.Repeated measurements: what is measured and what repeats? Statist Med 1990,9:639.
2,Armitage P, Berry G. Statistical methods in medical research. Oxford: Elickwell Scientific Publications, 1987,354~357.
3,方开泰编著.实用多元统计分析.上海:华东师范大学出版社,1989:132~136.
4,王学仁,王松桂编译.实用多元统计分析.上海:上海科学技术出版社,1990,177~182.
5,万崇华,方积乾,陈丽影,等.海洛因成瘾者生存质量测定量表的制定及其考评.中国行为医学科学杂志,1997,6(3):169.
收稿日期:1999-10-05, 百拇医药