总体参数的可信区间在医学研究中应用
作者：黄振学 刘希英 许小幸
单位：青岛医学院(青岛 266021)；黄振学 许小幸 预防医学教研室；刘希英 微生物学教研室
关键词：
青岛医学院学报990144 统计推断是统计研究的重要内容，主要包括两方面：参数估计和假设检验，而总体参数的可信区间是解决上述两项内容的重要手段，尤其在解决假设检验问题时更有独到之处。但是，由于可信区间的概念比较抽象，从而限制了其在医学中的应用。本文以实例阐明总体参数可信区间的意义及其在医学研究中的重要用途。
1 可信区间的意义
由样本指标推断正态分布资料的未知总体指标是抽样研究的目的之一。仅由样本统计量来估计总体参数称之为点估计，此法虽然简便，但未顾及抽样误差，而抽样误差在抽样研究中是不可避免的，因而，不能用概率来衡量估计的可信度。实际应用中，多采用区间估计来推断总体参数，即根据抽样误差的规律，按预先确定的概率(可信度)估计总体参数在哪个范围(区间)，所估计的区间叫做总体参数的可信区间。最常用估计的可信度为95%或99%，分别称作总体参数的95%可信区间或总体参数的99%可信区间。如由样本均数(
)推断总体均数(μ)的95%或99%可信区间，或由样本率(p)推断总体率(π)的95%或99%可信区间。95%可信区间是指该区间包括总体参数的概率为95%，即相当于每抽取100个含量相同的样本，分别计算出总体参数的95%可信区间,平均有95个可信区间包括总体参数，只有5个可信区间不包括总体参数。在统计学中，5%是小概率事件，实际发生的可能性小，因而实际应用中就认为总体参数在计算的可信区间之内。同样，99%的可信区间是指该区间包括总体参数的概率为99%，即相当于每抽取100个含量相同的样本，分别计算出总体参数的99%可信区间，平均有99个可信区间包括总体参数，只有1个可信区间不包括总体参数。1%的概率更小，实际发生的可能性更小，因而实际应用中就更有把握认为总体参数在计算的可信区间之内。
, 百拇医药
2 可信区间在参数估计中的应用
2.1 总体均数的区间估计
从正态分布总体中随机抽取含量为n的样本，可由样本均数估计未知总体均数的可信区间。当大样本(一般n>100)时，μ的95%可信区间为±1.96
＝-1.96～+1.96，μ的99%可信区间为±2.58＝-2.58～+2.58，式中为均数标准误的估计值。可信区间的两个端值称为可信限，-1.96或-2.58为可信区间的下限，+1.96或+2.58为可信区间的上限。可信区间是指上、下可信限为界的一个范围，样本均数作为总体均数的点估计位于总体均数的可信区间中心。当小样本(n<100)时，μ的95%可信区间为±t0.05(ν)＝-t0.05(ν)～+t0.05(ν)，μ的99%可信区间为±t0.01(ν)＝-t0.01(ν)～+t0.01(ν)，式中t0.05(ν)或t0.01(ν)为样本自由度为ν时的t值，可由统计用表的t界值表中查出。
, 百拇医药
例1，测得某地10名7岁男孩的体质量，计算得＝22.31kg，s＝2.74kg，＝0.87kg，则该地7岁男孩体质量总体均数的95%可信区间为22.31±2.262×0.87＝20.34～24.28(kg)；同样，该地7岁男孩体质量总体均数的99%可信区间为22.31±3.25×0.87＝19.48～25.14(kg).由上例可看出，若要提高估计总体均数的精密度，可通过加大样本含量来实现，因为n增大，变小，t值也减小，则可信区间的范围变窄。但是，在样本含量相同的情况下，若要提高估计总体均数的可信度，则必然会降低精密度，使可信区间的范围变宽。
2.2 总体率的区间估计
, 百拇医药 从某类总体率为π的两类构成总体中，随机抽取含量为n的样本，可由样本率(p)估计总体率(π)的可信区间。当nπ或n(1-π)≥5时，p近似服从正态分布，那么，π的95%可信区间为p±1.96sp＝(p-1.96sp)～(p+1.96sp)，π的99%可信区间为p±2.58sp＝(p-2.58sp)～(p+2.58sp)，式中sp为率标准误的估计值。
例2，从某地小学随机抽取女生85人，其中肺吸虫感染者13人，计算得p＝0.153，sp＝0.039，则该地小学女生肺吸虫感染总体率的95%可信区间为0.153±1.96×0.039＝0.077～0.229(7.7%～22.9%)，同样，该地小学女生肺吸虫感染总体率的99%可信区间为0.153±2.58×0.039＝0.052～0.254(5.2%～25.4%)。
, 百拇医药
3 可信区间在假设检验中的应用
假设检验是推断单个总体参数是否等于某已知总体参数，或推断两个总体参数的差别是否等于零(即两个总体参数是否相等)。假设检验只是对总体参数及其差别的质的推断，而区间估计则是对总体参数及其差别的量的推断，可以提供更多的信息，从而间接达到双侧假设检验的目的。
3.1 计量资料的假设检验
3.1.1 样本均数与总体均数的比较
例3，已知健康成年男子脉搏均数为72min-1，可视此为总体均数(μ0)，今从某山区抽样调查了25名健康成年男子脉搏，计算得＝74.2min-1，s＝6.5min-1，问该山区健康成年男子脉搏是否与一般健康成年男子脉搏有差异?因是小样本，采用t检验，计算得t＝1.692，t0.05(ν)＝2.064，P>0.05，差别无显著性。结论：尚不能认为该山区成年男子脉搏与一般健康成年男子有差异。根据此样本推断该山区健康成年男子脉搏总体均数的95%可信区间为74.2±2.064×6.5/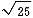
＝71.5～76.9min-1，该区间包括总体均数μ0＝72min-1，差别无显著性，结论与假设检验相同。
, 百拇医药
3.1.2 成对资料的比较
例4，应用某药治疗9例高血压病人，观察该药对舒张压有无作用。计算得治疗前、后舒张压的差值均数(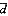
)＝0.52kPa，差值标准差(
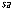)＝0.42kPa，差值标准误(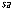)＝0.14kPa. 因是小样本，采用t检验，t＝3.714，t>t0.01(8)＝3.355，P<0.01，差别有极显著性。结论：该药有降低舒张压作用。根据此样本推断该药降低舒张压总体均数的99%可信区间为0.52±3.355×0.14＝0.05～0.99(kPa)，该区间因不包括
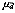＝0，差别有极显著性，结论与假设检验相同。
, 百拇医药
3.1.3 成组资料的比较
例5，测得某地20～24岁健康女子100人的收缩压1＝15.27kPa，1＝0.12kPa;又测该地20～24岁健康男子100人的收缩压2＝16.11kPa，2＝0.14kPa，问该地20～24岁健康男、女之间的收缩压均数相差有无显著性?因是大样本，采用u检验。计算得u＝4.565>2.58，P<0.01，差别有极显著性。结论：该地20～24岁健康人的收缩压男性高于女性。根据两样本推断两个正态分布总体均数差的99%可信区间，公式为｜1-2｜±2.581-2＝｜1-2｜-
, 百拇医药
2.581-2～｜1-2｜+2.581-2，式中1,2分别为两样本均数，1-2为两均数差的标准误。计算得1-2＝0.184kPa，则99%可信区间为｜15.27-16.11｜±2.58×0.184＝0.37～1.31(kPa)，该区间内不包括μ1-μ2＝0，差别有极显著性，结论与假设检验相同。
, http://www.100md.com
3.2 计数资料的假设检验
3.2.1 样本率与总体率的比较
例6，据以往经验，一般胃溃疡病人有20%发生胃出血(视为总体率π)，某医院观察65岁以上胃溃疡病人152例，有48例发生胃出血，问老年胃溃疡病人是否比一般胃溃疡病人容易发生胃出血?采用u检验，计算得p＝0.316，u＝3.625>2.58，p<0.01，差别有极显著性。结论：65岁以上老年胃溃疡病人比一般胃溃疡病病人容易发生胃出血。根据此样本推断65岁以上老年胃溃疡病人发生胃出血总体率的99%可信区间为0.316±2.58×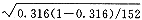
＝0.219～0.413(21.9%～41.3%)，该区间不包括总体率π＝20%，差别有极显著性，结论与假设检验相同。
3.2.2 两样本率的比较
, 百拇医药
例7，用甲药治疗小儿重症上呼吸道感染61例，45例有效；用乙药治疗同样病人55例，48例有效，问两组有效率有无差别?计算得p1＝0.7377，p2＝0.8727，sp1-p2 ＝0.0741，采用u检验，u＝1.822<1.96，P>0.05，差别无显著性。结论：两药治疗小儿重症上呼吸道感染有效率无差别。根据两样本推断两总体率差的95%可信区间，公式为｜p1-p2｜±1.96sp1-p2＝｜p1-p2｜-1.96sp1-p2～｜p1-p2｜+1.96sp1-p2，式中p1,p2分别为两样本率，sp1-p2为两率差的标准误，则95%可信区间为｜0.7377-0.8727｜±1.96×0.0741＝-0.0102～0.2802(-1.02%～28.02%)，该区间内包括π1-π2＝0，差别无显著性，结论与假设检验相同。
(1998-09-09收稿 1998-12-10修回), http://www.100md.com
单位：青岛医学院(青岛 266021)；黄振学 许小幸 预防医学教研室；刘希英 微生物学教研室
关键词：
青岛医学院学报990144 统计推断是统计研究的重要内容，主要包括两方面：参数估计和假设检验，而总体参数的可信区间是解决上述两项内容的重要手段，尤其在解决假设检验问题时更有独到之处。但是，由于可信区间的概念比较抽象，从而限制了其在医学中的应用。本文以实例阐明总体参数可信区间的意义及其在医学研究中的重要用途。
1 可信区间的意义
由样本指标推断正态分布资料的未知总体指标是抽样研究的目的之一。仅由样本统计量来估计总体参数称之为点估计，此法虽然简便，但未顾及抽样误差，而抽样误差在抽样研究中是不可避免的，因而，不能用概率来衡量估计的可信度。实际应用中，多采用区间估计来推断总体参数，即根据抽样误差的规律，按预先确定的概率(可信度)估计总体参数在哪个范围(区间)，所估计的区间叫做总体参数的可信区间。最常用估计的可信度为95%或99%，分别称作总体参数的95%可信区间或总体参数的99%可信区间。如由样本均数(
)推断总体均数(μ)的95%或99%可信区间，或由样本率(p)推断总体率(π)的95%或99%可信区间。95%可信区间是指该区间包括总体参数的概率为95%，即相当于每抽取100个含量相同的样本，分别计算出总体参数的95%可信区间,平均有95个可信区间包括总体参数，只有5个可信区间不包括总体参数。在统计学中，5%是小概率事件，实际发生的可能性小，因而实际应用中就认为总体参数在计算的可信区间之内。同样，99%的可信区间是指该区间包括总体参数的概率为99%，即相当于每抽取100个含量相同的样本，分别计算出总体参数的99%可信区间，平均有99个可信区间包括总体参数，只有1个可信区间不包括总体参数。1%的概率更小，实际发生的可能性更小，因而实际应用中就更有把握认为总体参数在计算的可信区间之内。, 百拇医药
2 可信区间在参数估计中的应用
2.1 总体均数的区间估计
从正态分布总体中随机抽取含量为n的样本，可由样本均数估计未知总体均数的可信区间。当大样本(一般n>100)时，μ的95%可信区间为
±1.96＝-1.96～+1.96，μ的99%可信区间为±2.58＝-2.58～+2.58，式中为均数标准误的估计值。可信区间的两个端值称为可信限，-1.96或-2.58为可信区间的下限，+1.96或+2.58为可信区间的上限。可信区间是指上、下可信限为界的一个范围，样本均数作为总体均数的点估计位于总体均数的可信区间中心。当小样本(n<100)时，μ的95%可信区间为±t0.05(ν)＝-t0.05(ν)～+t0.05(ν)，μ的99%可信区间为±t0.01(ν)＝-t0.01(ν)～+t0.01(ν)，式中t0.05(ν)或t0.01(ν)为样本自由度为ν时的t值，可由统计用表的t界值表中查出。, 百拇医药
例1，测得某地10名7岁男孩的体质量，计算得
＝22.31kg，s＝2.74kg，＝0.87kg，则该地7岁男孩体质量总体均数的95%可信区间为22.31±2.262×0.87＝20.34～24.28(kg)；同样，该地7岁男孩体质量总体均数的99%可信区间为22.31±3.25×0.87＝19.48～25.14(kg).由上例可看出，若要提高估计总体均数的精密度，可通过加大样本含量来实现，因为n增大，变小，t值也减小，则可信区间的范围变窄。但是，在样本含量相同的情况下，若要提高估计总体均数的可信度，则必然会降低精密度，使可信区间的范围变宽。2.2 总体率的区间估计
, 百拇医药 从某类总体率为π的两类构成总体中，随机抽取含量为n的样本，可由样本率(p)估计总体率(π)的可信区间。当nπ或n(1-π)≥5时，p近似服从正态分布，那么，π的95%可信区间为p±1.96sp＝(p-1.96sp)～(p+1.96sp)，π的99%可信区间为p±2.58sp＝(p-2.58sp)～(p+2.58sp)，式中sp为率标准误的估计值。
例2，从某地小学随机抽取女生85人，其中肺吸虫感染者13人，计算得p＝0.153，sp＝0.039，则该地小学女生肺吸虫感染总体率的95%可信区间为0.153±1.96×0.039＝0.077～0.229(7.7%～22.9%)，同样，该地小学女生肺吸虫感染总体率的99%可信区间为0.153±2.58×0.039＝0.052～0.254(5.2%～25.4%)。
, 百拇医药
3 可信区间在假设检验中的应用
假设检验是推断单个总体参数是否等于某已知总体参数，或推断两个总体参数的差别是否等于零(即两个总体参数是否相等)。假设检验只是对总体参数及其差别的质的推断，而区间估计则是对总体参数及其差别的量的推断，可以提供更多的信息，从而间接达到双侧假设检验的目的。
3.1 计量资料的假设检验
3.1.1 样本均数与总体均数的比较
例3，已知健康成年男子脉搏均数为72min-1，可视此为总体均数(μ0)，今从某山区抽样调查了25名健康成年男子脉搏，计算得
＝74.2min-1，s＝6.5min-1，问该山区健康成年男子脉搏是否与一般健康成年男子脉搏有差异?因是小样本，采用t检验，计算得t＝1.692，t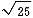＝71.5～76.9min-1，该区间包括总体均数μ0＝72min-1，差别无显著性，结论与假设检验相同。, 百拇医药
3.1.2 成对资料的比较
例4，应用某药治疗9例高血压病人，观察该药对舒张压有无作用。计算得治疗前、后舒张压的差值均数(
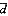)＝0.52kPa，差值标准差(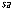)＝0.42kPa，差值标准误(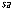)＝0.14kPa. 因是小样本，采用t检验，t＝3.714，t>t0.01(8)＝3.355，P<0.01，差别有极显著性。结论：该药有降低舒张压作用。根据此样本推断该药降低舒张压总体均数的99%可信区间为0.52±3.355×0.14＝0.05～0.99(kPa)，该区间因不包括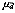＝0，差别有极显著性，结论与假设检验相同。, 百拇医药
3.1.3 成组资料的比较
例5，测得某地20～24岁健康女子100人的收缩压
1＝15.27kPa，1＝0.12kPa;又测该地20～24岁健康男子100人的收缩压2＝16.11kPa，2＝0.14kPa，问该地20～24岁健康男、女之间的收缩压均数相差有无显著性?因是大样本，采用u检验。计算得u＝4.565>2.58，P<0.01，差别有极显著性。结论：该地20～24岁健康人的收缩压男性高于女性。根据两样本推断两个正态分布总体均数差的99%可信区间，公式为｜1-2｜±2.581-2＝｜1-2｜-, 百拇医药
2.58
1-2～｜1-2｜+2.581-2，式中1,2分别为两样本均数，1-2为两均数差的标准误。计算得1-2＝0.184kPa，则99%可信区间为｜15.27-16.11｜±2.58×0.184＝0.37～1.31(kPa)，该区间内不包括μ1-μ2＝0，差别有极显著性，结论与假设检验相同。, http://www.100md.com
3.2 计数资料的假设检验
3.2.1 样本率与总体率的比较
例6，据以往经验，一般胃溃疡病人有20%发生胃出血(视为总体率π)，某医院观察65岁以上胃溃疡病人152例，有48例发生胃出血，问老年胃溃疡病人是否比一般胃溃疡病人容易发生胃出血?采用u检验，计算得p＝0.316，u＝3.625>2.58，p<0.01，差别有极显著性。结论：65岁以上老年胃溃疡病人比一般胃溃疡病病人容易发生胃出血。根据此样本推断65岁以上老年胃溃疡病人发生胃出血总体率的99%可信区间为0.316±2.58×
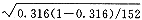＝0.219～0.413(21.9%～41.3%)，该区间不包括总体率π＝20%，差别有极显著性，结论与假设检验相同。3.2.2 两样本率的比较
, 百拇医药
例7，用甲药治疗小儿重症上呼吸道感染61例，45例有效；用乙药治疗同样病人55例，48例有效，问两组有效率有无差别?计算得p1＝0.7377，p2＝0.8727，sp1-p2 ＝0.0741，采用u检验，u＝1.822<1.96，P>0.05，差别无显著性。结论：两药治疗小儿重症上呼吸道感染有效率无差别。根据两样本推断两总体率差的95%可信区间，公式为｜p1-p2｜±1.96sp1-p2＝｜p1-p2｜-1.96sp1-p2～｜p1-p2｜+1.96sp1-p2，式中p1,p2分别为两样本率，sp1-p2为两率差的标准误，则95%可信区间为｜0.7377-0.8727｜±1.96×0.0741＝-0.0102～0.2802(-1.02%～28.02%)，该区间内包括π1-π2＝0，差别无显著性，结论与假设检验相同。
(1998-09-09收稿 1998-12-10修回), http://www.100md.com