基于PC机的多导联心电图测试系统与检测处理算法
作者:张红煊 王泽 朱贻盛
单位:上海交通大学生命科学学院生物医学工程系 上海 200030
关键词:多导联;心电信号;心率过速和心室纤颤;虚拟仪器;非线性动力学;复杂度
北京生物医学工程000407 摘 要 本文分析描述了基于PC机的心电信号的测试系统,并讨论了一些技术细节。进而我们建立相应的线性和非线性的检测方法与算法,以帮助临床医生分析和诊断心率过速和心室纤颤。根据我们实验记录的数据和算法的结果,这套测试系统显示出良好的特性,可以为心率过速和心室纤颤的自动检测提供一个可行有效的途径。
PC Based Multi-Lead ECG Test & Measurement System And Processing Algorithm
Zhang Hongxuan,Wang Ze,Zhu Yisheng
, 百拇医药
(Dept. of Biomedical Engineering,Shanghai Jiaotong University, 200030)
Abstract In this paper is described a PC based ECG signal test & measurement system and some technical details are discussed.We set up linear and nonlinear detection methods and algorithms in order to hepl clinic doctors diagnose VT and VF. From data recorded and result of computation, this set of system has good performance. It might be a practical way of doing automatic VT and VF test & measurement.
, 百拇医药
Key words:Multi-lead, ECG, VT and VF, Virtual instrument, Nonlinear dynamics, Complexity
0 引 言
心电图学的发展史是一部新技术引入、新导联发现和新学说提出的历史。从1856年Muller和Kolliker发现蛙心舒缩运动时伴有电活动,到1887年的Waller用Maregy研制的Lippmann微电计首次在人体中记录到心电活动,到1903年Einthoven在Van der woerd的帮助下制造了第一台弦线型心电计,到1909年Waller在英国皇家科学院公开演示而得到学术界的正式认可,到今天,心电图的记录已经经过了很多代的发展:从弦线式到电子管式,从示波器式到晶体管式,到今天的超大规模集成电路式。本文主要集中讨论当今基于PC机的大规模集成电路的心电图的测试系统。心脏是具有特殊的电传导系统,并且它的生理和化学组成决定了它的各向异性。心脏的电传导由窦房结发出的兴奋,按照一定的途径和时程,依次向心房和心室扩布,引起整个心脏的循环兴奋。心脏各部分兴奋过程中出现的电位变化的方向、途径、次序和时间等均有一定的规律。由于人体为一个容积导体,这种电变化必然扩布到身体表面,使心电信息的体外电检测成为可能。鉴于心脏在同一时间内产生大量的电信号,因此,可通过安放在身体表面的电极,将电位变化以时间为函数记录下来,也就是心电图ECG(Electro Cardio Gram)。由于放在体表的电极测出的ECG信号随着不同位置而异。心周期中某段ECG信号描述在这一电极位置不明显,而在另一位置上却很清楚。为了完整描述心脏的活动状况,常用在水平和垂直方向的十二种不同的导联作记录,以看清个重要的细节。心电信号通过导线和电极加到心电图机放大器的输入端,一般把导线和电极合在一起称为导联。
, 百拇医药
1 基于PC机的多导联的心电图测量系统的研制
近百年来,国外曾试用过百余种导联系统,Einthoven 1903年提出了标准Ⅰ、Ⅱ、Ⅲ导联,30年代Wilson提出了V1~V6单极胸导联,40年代的Goldberger改良了中心电端,提出了aVR\,aVL\,aVF单极加压肢体导联。经过了长期的临床实践确立了目前的12导联的常规地位。我们这套基于PC机的多导联的心电测试系统也是基于目前的12导联的测量系统[1]。12导联的心电图测试系统框架图如图1所示。
图1 多导联心电图测量及信号处理框架
在建立多导联心电测量系统后,我们设计研制了心电信号测试系统,它主要包括两部分:多导联模拟心电信号的数字测试卡和环境测试卡。多导联模拟心电图采集测试卡的研制主要包括:数字插卡与计算机总线的接口,增益可程控的多路A/D循环采集系统,多功能的时钟及控制电路,输入模拟信号的调理和前置滤波电路,以及电源等。环境测试卡主要利用在分析测试者的状态和周围的环境对测试心电图的影响以及将来的测试扩展。
, 百拇医药
2 多导联心电图的信号检测算法及实验仿真
关于12导联的一些法则,如:Einthoven法则等,在这里不再累述。12导联分为:双极肢体导联,单极肢体导联,加压单极肢体导联和单极胸导联。我们利用12导联所记录的心电图数据,主要用来判断VT和VF信号。关于12导联的心电数据合成,Einthoven,Goldberger和Langner等已经作了许多重要的工作[1]。在这里主要利用现有的方法进行滤波,从而进行心电信号的VT和VF的检测。
关于VT和VF的检测,许多学者都对它进行过研究。这里提出一些算法是根据张绪省博士论文中提出的思路进行的,其中的大部分算法主要是从非线性动力学的角度出发的。
(1)频谱法与直方图分析
为了研究系统的统计特性,对时间序列作频谱分析是最常用的数值方法。我们这里研究12导联的信号主要是从非线性动力学方面来着手,研究的时间序列所具有的频谱特性。
, 百拇医药
直方图的分析可以利用很多参数,如:概率密度,能量分布和频谱的密度分布等。直方图分析是很经典的随机信号处理方法,这里使用直方图分析主要是得到正常心电信号,VT信号和VF信号的能量和密度的分布的差异。
从频谱及频谱的幅度信息直方图可以看出:从心脏正常的窦性节律到心率过速,到心室纤颤,心脏从正常到猝死前的心室纤颤,整个过程是相关联的[2]。
(2)相关维数
相关维数的是分形理论的发展中一个重要的里程碑。相关维数的计算可以有很多不同的形式与方法。我们这里利用的相关维数主要是针对单变量的时间序列分析。由Takens在1981年提出的嵌入定理[3],将时间序列延拓到m维空间,从而分析延拓空间的吸引子的结构特性。
考察m维(m足够大)相空间中的一对相点:
, 百拇医药
xm(ti)∶(x(ti),x(ti+τ),Λ,x(ti+(m-1)τ)
xm(tj)∶(x(tj),x(tj+τ),Λ,x(tj+(m-1)τ)
设它们之间的距离(即Euclidean模)为rij(m),显然rij(m)是相空间维数m的函数,且:
rij(m)=‖xm(ti)-xm(tj)‖ (1)
这里‖.‖表示Euclidean模。
, 百拇医药
给定一临界距离r(r为一小的数),检查有多少对相点(xi,xj)之间的距离小于r,并把距离小于r的“点对”在所有“点对”中所占的比例记为: (2)
(2)
其中,N=n-(m-1)τ为相点数,θ是Heaviside函数。
现在考察一下C2(r,m)与r的关系。给定一个微量δ,用δ来探测吸引子的结构。如果吸引子结构是一维的线型,则在与相对于参考定点的距离在r以内的相关点数将正比于r/δ;如果吸引子的结构是二维的面型,则所对应的相关点数将正比于(r/δ)2,如此类推可知,如果吸引子的结构是D2维的流型,则所对应的相关点数应正比于(r/δ)D2,即C2(r,m)∝rD2
, 百拇医药
由于上式的比例关系与所取的试探量的取值无关,所取比例系数为一个单位时间,有
C2(r,m)=rD2(m)
(3)
则 (4)
(4)
上式所定义的D2(m)就是所谓的相关维数。按上式算出的D2显然与所嵌入的相空间的维数m有关,即D2是m的函数。故一般称D2(m)是相关维数D2的估计值[4]。
利用相关维数不但能够清晰地观察到心电系统的分形特征,而且也易于和一般的随机系统分开。
, 百拇医药
(3)Lyapunov指数
Lyapunov指数也是在时间序列的延拓和重构m维空间的基础上,进行系统动态特征提取的。我们这里也是针对一维的心电信号的时间序列,主要是根据两个相邻参考点的距离特征,在随着时间的变化而发生的变异特性。它主要可以描述系统的发散和稳定特性[4,5]。
①应用时间序列重构m维相空间。
②选取使各相空间坐标相关性最小的τ。
③如图2所示,在延拓的m维相空间里,取初始相点A(t1)为参考点,其m个分量为:(x(t1),x(t1+τ),Λ,x(t1+(m-1)τ)。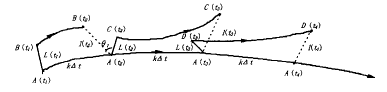
, http://www.100md.com
图2 最大Lyapunov指数计算示意图
根据下式: (5)
(5)
可求得A(t1)的最近邻点B(t1),这里MIN为取最小函数。Lnbt表示在欧几里德意义上A(t1)与其最近邻点B(t1)的距离。以A(t1)和B(t1)为端点构成一个初始向量,记为 (t1),算出其长度,并记为L(t1)。向量
(t1),算出其长度,并记为L(t1)。向量 (t1)沿轨线向前发展,设在时间t2=t1+kδt时,A(t1)点演化到A2(t2)点,同时B(t1)演化到B(t2),即得到一个新的向量V′→(t1),其长度为l(t2)。如果用ζ1表示在此时间内向量长度的指数增长率,则
(t1)沿轨线向前发展,设在时间t2=t1+kδt时,A(t1)点演化到A2(t2)点,同时B(t1)演化到B(t2),即得到一个新的向量V′→(t1),其长度为l(t2)。如果用ζ1表示在此时间内向量长度的指数增长率,则
, 百拇医药
l(t2)=L(t1)eζ1kΔt (6)
其中取δt=1。(一个采样单位时间)
④在A(t2)的若干个最近邻点中找出一个满足θ1角很小的近邻点C(t2),(若无法满足小θ1和近邻两条件,仍以B(t1)为新的初始点)。这样得到向量V→(t2),其长度为L(t2),设在时间t3=t2+kδt时,A(t2)发展到A(t3),而C(t2)发展到C(t3),即向量演变为V′→(t2),长度为l(t3),则 (7)
(7)
, http://www.100md.com
重复上述过程一直进行到点集{xi,i=1,2,Λ,N}的终点,最后取指数增长率λi的平均值为最大Lyapunov指数的估计值 (8)
(8)
这里n表示发展的总步数, ,k为步长,LE1(m)的单位(bit/s),表示单位时间内信息量的变化。
,k为步长,LE1(m)的单位(bit/s),表示单位时间内信息量的变化。
⑤依次增加嵌入空间的维数m,重复上述(3)—(4)步骤,直到指数的估计值LE1(m)保持平稳为止。
记
LE1(m0)=LE1(m0+1)=LE1(m0+2)=…=LE1
, 百拇医药
(9)
此时得到的LE1就是最大Lyapunov指数。
(4)Lempel-Ziv复杂度
从动力学的观点来说,稳态、周期或准周期运动都是有序的并不复杂,而当动力系统的运动进入混沌时就成为复杂的了。复杂程度的定量刻划显得很重要。根据Kolmogorov[6],某给定“0-1”序列的复杂性是由产生该序列的最短计算机程序的比特数决定的。但这没有通用算法。本文采用Lempel-Ziv算法[6],通过两种简单操作(复制和添加)的计算模型来描述一个给定序列,并将所需的添加操作次数作为序列的复杂性度量。反映了给定序列随其长度的增长出现新模式的速率。Kaspar和Schuste根据此定义研制了复杂度c(n)的算法,并将其用于单峰映射和一维元胞自动机的分析上。该算法的实质是不断比较某一字符串是否是另一字符串的子串,是,则复杂度维持不变,否则加一[7,8]。
, 百拇医药
设给定序列为
S1S2…Sn
从空串(不含任何符号的符号串)出发开始添加S1。现考虑中间步骤,设已生成前缀S1S2ΛSr-1,rr是用添加操作完成的,记为
S1S2ΛSn→S1.S2ΛSr-1S\-r.Sr+1
这里在Sr后的记号“.”反映了Sr的生成过程(添加)。现给出如何做下去的法则。
, http://www.100md.com
先令S=S1S2…Sr,Q=Sr+1。用SQ表示把S,Q两个符号串拼接成的总字符串,SQπ表示把SQ中最后一个字符删去所得的字符串(π表示去掉它前面的符号串的最后一个符号的操作),观察Q是否可以从SQπ用复制方法得到。在这里即是有SQπ=S1S2…Sr。
如果Q不能从SQπ中某个子串复制得到,就用添加操作加上Sr+1,并加上一个记号“.”,又回到与刚才相同的情况。
如果Q=Sr+1可以从SQπ中某个符号复制得到,则继续观察Q=Sr+1Sr+2能否从SQπ的某个子串复制得到,这时
SQπ=S1S2…SrSr+1
, 百拇医药
如果能办到,再考虑Q=Sr+1Sr+2Sr+3,并提出同样问题。这样下去有两种可能,或者Q已包含了原来给定序列的最后一个符号Sn,分析结束;或者对某个Q,它不再能从SQπ的任何一个子串复制得到,这时就取添加操作,将这个Q的最后一个符号添上,并在它后面加上记号“.”。实际的记号“.”的个数就反映了采取添加操作的次数。这样,原给定符号串被“.”分成段的数目就定义为“复杂度”c(n)。
3 实验结果与结论
这里心电信号的采样数据的频率为200Hz。从时域的信号图中,我们可以看出,VT和VF的混乱程度不一样,但它们的心率都在200次/分钟以上,VF比VT的频率更高,也更混乱,但我们从现有的线性数字信号处理算法无法分辨出它们及建立他们之间的联系。在频谱的分析中,我们可以发现VT的频谱的分布较窄,呈现的周期性强,旁瓣明显,而VF信号的周期性弱,而且呈现出典型的1/f分布,找不到明显的频谱旁瓣;而且在图4的(a)和(b)中,我们能清晰的分辨出第一频谱波峰的位置差异,VF信号的主要成分的频率分量分布在7Hz~9Hz之间,而VT的第一频谱波峰分布在4~5Hz之间;正常人的心率大约为60~90次/分钟,而实验中的VT的频率是大约200~250次/分钟,属于心率过速,VF的心率大约为400~500次/分钟,到这时心脏已经失去了博血的功能,为保护病人的健康,应立即进行电击除颤,以消除正常的窦房结以外的异位起博点的随机搏动。图4中VT和VF的直方图更验证了这种现象,从近代非线性理论的角度来说,VT和VF的动力学特性呈现出非线性动力学特性;VT和VF的直方图还说明了心脏从正常的窦性节律到心率过速,心电信号能量的分布发生了变化,到了心室纤颤阶段,心脏已经完全失去了正常的节律,已经分辨不出QRS波及其所具有的能量分布。VT和VF的频谱分布充分说明了信号具有非线性的特征。在图5和图6中我们利用相关维数和Lyapunov指数来研究心电信号的特征。相关维数和Lyapunov指数是非线性动力学发展中的动力学特征指标,在我们的研究中发现,VT和VF的相关维数呈分数维变化,并且VF的相关维数明显大于VT。Lyapunov指数的研究说明了心脏的非线性动力学特征,VT和VF计算的值相差不大,但VT和VF的Lyapunov指数都大于零,呈现出混沌特性。在图6中,我们计算了VT和VF的Lempel-Ziv复杂度,VT和VF各35条,其中代表VF信号,0代表VT信号,从计算出的复杂度对照图中看VF的复杂度明显的大于VT的复杂度(VF的复杂度的平均值为58,VT的复杂度的平均值为32);从复杂性动力学角度来看,VF的动力学行为更难以预测;在实验中,我们采集研究并发现心脏从窦性节律到心率过速,到心室纤颤,它们的平均复杂度基本上成倍数增长,在临床医学的心脏疾病的诊断中,我们可以建立复杂度阈值检测,为准确判断和及时的电击除颤提供一定的依据。从研究和仿真的结果可以表明:本多导联心电测量和分析系统具有良好的性能:多导联的数据采集程控性能高,上述虚拟仪器的控制灵活,非线性心电信号分析方法实用,VT和VF的分辨率高。在我们所测的心电数据下,VT与VF的识别率达到95%以上。本套虚拟多导联心电测试仪器在临床上具有广阔的前景。
, http://www.100md.com
图3 (a)VT时域信号
图4 (a)VT的频谱图
图3 (b)VF时域信号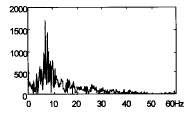
图4 (b)VF的频谱图
图5 (a)VT信号的频谱幅度信息直方图
图5 (b)VF信号的频谱幅度信息直方图
, 百拇医药
图6 (a)VF的相关维数D2(m)与嵌入维数m函数关系图
图6 (b)心室纤颤节律下lgC2(r,m)~lgr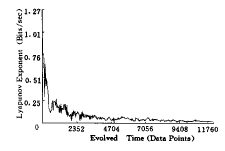
图7 VT和VF的Lyapunov指数图
图8 VT和VF复杂度对比图
基金项目:本课题承国家自然科学基金资助。
作者简介:张红煊(1972—),男,上海交通大学生物医学工程系博士研究生。
, 百拇医药
参考文献
[1] 张开滋,刘海洋,吴杰.心电信息学.第一版.科学技术文献出版社,1998,pp.3-45
[2] Takens F. Detecting strange attractors in turbulence. In:Rand DA, Young LS (eds),Dynamical system and turbulence, lecture notes in mathematics, Springer, Berlin,1981,898:366-387
[3] 张绪省.心室纤颤动力学特性的非线性分析及应用研究.上海交通大学博士论文,1997
[4] Zhang Xusheng, Zhu Yisheng. New approach to studies on ECG dynamics:extraction and analyses of QRS complex irregularity tome series. Medical & Biological Engineering & Computing,1997,pp.467-473
, 百拇医药
[5] Radhakrishnan N, Gangadhar BN. Estimating regularity in epileptic seizure time-series data. IEEE Engineering in Medicine and Biology,1998,pp.89-94
[6] 谢惠民.复杂性与动力系统.第一版,1994,pp.186-211
[7] Starrobin JM, Wgarton JM, Shander GS. Comparative analysis of polymorphic ventricular tachyarrhymias and fibrillation:clinical observations and numerical experiments. Computer in Cardiology,1998,25:25~28
[8] Zhang Xusheng, Zhu Yisheng, Thakor NV. Detecting ventricular tachycardia and fibrillation by complexity measure. IEEE Trans Biomed Eng,1999,46(5):548-555
(1999-10-20收稿), http://www.100md.com
单位:上海交通大学生命科学学院生物医学工程系 上海 200030
关键词:多导联;心电信号;心率过速和心室纤颤;虚拟仪器;非线性动力学;复杂度
北京生物医学工程000407 摘 要 本文分析描述了基于PC机的心电信号的测试系统,并讨论了一些技术细节。进而我们建立相应的线性和非线性的检测方法与算法,以帮助临床医生分析和诊断心率过速和心室纤颤。根据我们实验记录的数据和算法的结果,这套测试系统显示出良好的特性,可以为心率过速和心室纤颤的自动检测提供一个可行有效的途径。
PC Based Multi-Lead ECG Test & Measurement System And Processing Algorithm
Zhang Hongxuan,Wang Ze,Zhu Yisheng
, 百拇医药
(Dept. of Biomedical Engineering,Shanghai Jiaotong University, 200030)
Abstract In this paper is described a PC based ECG signal test & measurement system and some technical details are discussed.We set up linear and nonlinear detection methods and algorithms in order to hepl clinic doctors diagnose VT and VF. From data recorded and result of computation, this set of system has good performance. It might be a practical way of doing automatic VT and VF test & measurement.
, 百拇医药
Key words:Multi-lead, ECG, VT and VF, Virtual instrument, Nonlinear dynamics, Complexity
0 引 言
心电图学的发展史是一部新技术引入、新导联发现和新学说提出的历史。从1856年Muller和Kolliker发现蛙心舒缩运动时伴有电活动,到1887年的Waller用Maregy研制的Lippmann微电计首次在人体中记录到心电活动,到1903年Einthoven在Van der woerd的帮助下制造了第一台弦线型心电计,到1909年Waller在英国皇家科学院公开演示而得到学术界的正式认可,到今天,心电图的记录已经经过了很多代的发展:从弦线式到电子管式,从示波器式到晶体管式,到今天的超大规模集成电路式。本文主要集中讨论当今基于PC机的大规模集成电路的心电图的测试系统。心脏是具有特殊的电传导系统,并且它的生理和化学组成决定了它的各向异性。心脏的电传导由窦房结发出的兴奋,按照一定的途径和时程,依次向心房和心室扩布,引起整个心脏的循环兴奋。心脏各部分兴奋过程中出现的电位变化的方向、途径、次序和时间等均有一定的规律。由于人体为一个容积导体,这种电变化必然扩布到身体表面,使心电信息的体外电检测成为可能。鉴于心脏在同一时间内产生大量的电信号,因此,可通过安放在身体表面的电极,将电位变化以时间为函数记录下来,也就是心电图ECG(Electro Cardio Gram)。由于放在体表的电极测出的ECG信号随着不同位置而异。心周期中某段ECG信号描述在这一电极位置不明显,而在另一位置上却很清楚。为了完整描述心脏的活动状况,常用在水平和垂直方向的十二种不同的导联作记录,以看清个重要的细节。心电信号通过导线和电极加到心电图机放大器的输入端,一般把导线和电极合在一起称为导联。
, 百拇医药
1 基于PC机的多导联的心电图测量系统的研制
近百年来,国外曾试用过百余种导联系统,Einthoven 1903年提出了标准Ⅰ、Ⅱ、Ⅲ导联,30年代Wilson提出了V1~V6单极胸导联,40年代的Goldberger改良了中心电端,提出了aVR\,aVL\,aVF单极加压肢体导联。经过了长期的临床实践确立了目前的12导联的常规地位。我们这套基于PC机的多导联的心电测试系统也是基于目前的12导联的测量系统[1]。12导联的心电图测试系统框架图如图1所示。

图1 多导联心电图测量及信号处理框架
在建立多导联心电测量系统后,我们设计研制了心电信号测试系统,它主要包括两部分:多导联模拟心电信号的数字测试卡和环境测试卡。多导联模拟心电图采集测试卡的研制主要包括:数字插卡与计算机总线的接口,增益可程控的多路A/D循环采集系统,多功能的时钟及控制电路,输入模拟信号的调理和前置滤波电路,以及电源等。环境测试卡主要利用在分析测试者的状态和周围的环境对测试心电图的影响以及将来的测试扩展。
, 百拇医药
2 多导联心电图的信号检测算法及实验仿真
关于12导联的一些法则,如:Einthoven法则等,在这里不再累述。12导联分为:双极肢体导联,单极肢体导联,加压单极肢体导联和单极胸导联。我们利用12导联所记录的心电图数据,主要用来判断VT和VF信号。关于12导联的心电数据合成,Einthoven,Goldberger和Langner等已经作了许多重要的工作[1]。在这里主要利用现有的方法进行滤波,从而进行心电信号的VT和VF的检测。
关于VT和VF的检测,许多学者都对它进行过研究。这里提出一些算法是根据张绪省博士论文中提出的思路进行的,其中的大部分算法主要是从非线性动力学的角度出发的。
(1)频谱法与直方图分析
为了研究系统的统计特性,对时间序列作频谱分析是最常用的数值方法。我们这里研究12导联的信号主要是从非线性动力学方面来着手,研究的时间序列所具有的频谱特性。
, 百拇医药
直方图的分析可以利用很多参数,如:概率密度,能量分布和频谱的密度分布等。直方图分析是很经典的随机信号处理方法,这里使用直方图分析主要是得到正常心电信号,VT信号和VF信号的能量和密度的分布的差异。
从频谱及频谱的幅度信息直方图可以看出:从心脏正常的窦性节律到心率过速,到心室纤颤,心脏从正常到猝死前的心室纤颤,整个过程是相关联的[2]。
(2)相关维数
相关维数的是分形理论的发展中一个重要的里程碑。相关维数的计算可以有很多不同的形式与方法。我们这里利用的相关维数主要是针对单变量的时间序列分析。由Takens在1981年提出的嵌入定理[3],将时间序列延拓到m维空间,从而分析延拓空间的吸引子的结构特性。
考察m维(m足够大)相空间中的一对相点:
, 百拇医药
xm(ti)∶(x(ti),x(ti+τ),Λ,x(ti+(m-1)τ)
xm(tj)∶(x(tj),x(tj+τ),Λ,x(tj+(m-1)τ)
设它们之间的距离(即Euclidean模)为rij(m),显然rij(m)是相空间维数m的函数,且:
rij(m)=‖xm(ti)-xm(tj)‖ (1)
这里‖.‖表示Euclidean模。
, 百拇医药
给定一临界距离r(r为一小的数),检查有多少对相点(xi,xj)之间的距离小于r,并把距离小于r的“点对”在所有“点对”中所占的比例记为:
 (2)
(2)其中,N=n-(m-1)τ为相点数,θ是Heaviside函数。
现在考察一下C2(r,m)与r的关系。给定一个微量δ,用δ来探测吸引子的结构。如果吸引子结构是一维的线型,则在与相对于参考定点的距离在r以内的相关点数将正比于r/δ;如果吸引子的结构是二维的面型,则所对应的相关点数将正比于(r/δ)2,如此类推可知,如果吸引子的结构是D2维的流型,则所对应的相关点数应正比于(r/δ)D2,即C2(r,m)∝rD2
, 百拇医药
由于上式的比例关系与所取的试探量的取值无关,所取比例系数为一个单位时间,有
C2(r,m)=rD2(m)
(3)
则
 (4)
(4)上式所定义的D2(m)就是所谓的相关维数。按上式算出的D2显然与所嵌入的相空间的维数m有关,即D2是m的函数。故一般称D2(m)是相关维数D2的估计值[4]。
利用相关维数不但能够清晰地观察到心电系统的分形特征,而且也易于和一般的随机系统分开。
, 百拇医药
(3)Lyapunov指数
Lyapunov指数也是在时间序列的延拓和重构m维空间的基础上,进行系统动态特征提取的。我们这里也是针对一维的心电信号的时间序列,主要是根据两个相邻参考点的距离特征,在随着时间的变化而发生的变异特性。它主要可以描述系统的发散和稳定特性[4,5]。
①应用时间序列重构m维相空间。
②选取使各相空间坐标相关性最小的τ。
③如图2所示,在延拓的m维相空间里,取初始相点A(t1)为参考点,其m个分量为:(x(t1),x(t1+τ),Λ,x(t1+(m-1)τ)。

, http://www.100md.com
图2 最大Lyapunov指数计算示意图
根据下式:
 (5)
(5)可求得A(t1)的最近邻点B(t1),这里MIN为取最小函数。Lnbt表示在欧几里德意义上A(t1)与其最近邻点B(t1)的距离。以A(t1)和B(t1)为端点构成一个初始向量,记为
 (t1),算出其长度,并记为L(t1)。向量
(t1),算出其长度,并记为L(t1)。向量 (t1)沿轨线向前发展,设在时间t2=t1+kδt时,A(t1)点演化到A2(t2)点,同时B(t1)演化到B(t2),即得到一个新的向量V′→(t1),其长度为l(t2)。如果用ζ1表示在此时间内向量长度的指数增长率,则
(t1)沿轨线向前发展,设在时间t2=t1+kδt时,A(t1)点演化到A2(t2)点,同时B(t1)演化到B(t2),即得到一个新的向量V′→(t1),其长度为l(t2)。如果用ζ1表示在此时间内向量长度的指数增长率,则, 百拇医药
l(t2)=L(t1)eζ1kΔt (6)
其中取δt=1。(一个采样单位时间)
④在A(t2)的若干个最近邻点中找出一个满足θ1角很小的近邻点C(t2),(若无法满足小θ1和近邻两条件,仍以B(t1)为新的初始点)。这样得到向量V→(t2),其长度为L(t2),设在时间t3=t2+kδt时,A(t2)发展到A(t3),而C(t2)发展到C(t3),即向量演变为V′→(t2),长度为l(t3),则
 (7)
(7), http://www.100md.com
重复上述过程一直进行到点集{xi,i=1,2,Λ,N}的终点,最后取指数增长率λi的平均值为最大Lyapunov指数的估计值
 (8)
(8)这里n表示发展的总步数,
 ,k为步长,LE1(m)的单位(bit/s),表示单位时间内信息量的变化。
,k为步长,LE1(m)的单位(bit/s),表示单位时间内信息量的变化。⑤依次增加嵌入空间的维数m,重复上述(3)—(4)步骤,直到指数的估计值LE1(m)保持平稳为止。
记
LE1(m0)=LE1(m0+1)=LE1(m0+2)=…=LE1
, 百拇医药
(9)
此时得到的LE1就是最大Lyapunov指数。
(4)Lempel-Ziv复杂度
从动力学的观点来说,稳态、周期或准周期运动都是有序的并不复杂,而当动力系统的运动进入混沌时就成为复杂的了。复杂程度的定量刻划显得很重要。根据Kolmogorov[6],某给定“0-1”序列的复杂性是由产生该序列的最短计算机程序的比特数决定的。但这没有通用算法。本文采用Lempel-Ziv算法[6],通过两种简单操作(复制和添加)的计算模型来描述一个给定序列,并将所需的添加操作次数作为序列的复杂性度量。反映了给定序列随其长度的增长出现新模式的速率。Kaspar和Schuste根据此定义研制了复杂度c(n)的算法,并将其用于单峰映射和一维元胞自动机的分析上。该算法的实质是不断比较某一字符串是否是另一字符串的子串,是,则复杂度维持不变,否则加一[7,8]。
, 百拇医药
设给定序列为
S1S2…Sn
从空串(不含任何符号的符号串)出发开始添加S1。现考虑中间步骤,设已生成前缀S1S2ΛSr-1,r
S1S2ΛSn→S1.S2ΛSr-1S\-r.Sr+1
这里在Sr后的记号“.”反映了Sr的生成过程(添加)。现给出如何做下去的法则。
, http://www.100md.com
先令S=S1S2…Sr,Q=Sr+1。用SQ表示把S,Q两个符号串拼接成的总字符串,SQπ表示把SQ中最后一个字符删去所得的字符串(π表示去掉它前面的符号串的最后一个符号的操作),观察Q是否可以从SQπ用复制方法得到。在这里即是有SQπ=S1S2…Sr。
如果Q不能从SQπ中某个子串复制得到,就用添加操作加上Sr+1,并加上一个记号“.”,又回到与刚才相同的情况。
如果Q=Sr+1可以从SQπ中某个符号复制得到,则继续观察Q=Sr+1Sr+2能否从SQπ的某个子串复制得到,这时
SQπ=S1S2…SrSr+1
, 百拇医药
如果能办到,再考虑Q=Sr+1Sr+2Sr+3,并提出同样问题。这样下去有两种可能,或者Q已包含了原来给定序列的最后一个符号Sn,分析结束;或者对某个Q,它不再能从SQπ的任何一个子串复制得到,这时就取添加操作,将这个Q的最后一个符号添上,并在它后面加上记号“.”。实际的记号“.”的个数就反映了采取添加操作的次数。这样,原给定符号串被“.”分成段的数目就定义为“复杂度”c(n)。
3 实验结果与结论
这里心电信号的采样数据的频率为200Hz。从时域的信号图中,我们可以看出,VT和VF的混乱程度不一样,但它们的心率都在200次/分钟以上,VF比VT的频率更高,也更混乱,但我们从现有的线性数字信号处理算法无法分辨出它们及建立他们之间的联系。在频谱的分析中,我们可以发现VT的频谱的分布较窄,呈现的周期性强,旁瓣明显,而VF信号的周期性弱,而且呈现出典型的1/f分布,找不到明显的频谱旁瓣;而且在图4的(a)和(b)中,我们能清晰的分辨出第一频谱波峰的位置差异,VF信号的主要成分的频率分量分布在7Hz~9Hz之间,而VT的第一频谱波峰分布在4~5Hz之间;正常人的心率大约为60~90次/分钟,而实验中的VT的频率是大约200~250次/分钟,属于心率过速,VF的心率大约为400~500次/分钟,到这时心脏已经失去了博血的功能,为保护病人的健康,应立即进行电击除颤,以消除正常的窦房结以外的异位起博点的随机搏动。图4中VT和VF的直方图更验证了这种现象,从近代非线性理论的角度来说,VT和VF的动力学特性呈现出非线性动力学特性;VT和VF的直方图还说明了心脏从正常的窦性节律到心率过速,心电信号能量的分布发生了变化,到了心室纤颤阶段,心脏已经完全失去了正常的节律,已经分辨不出QRS波及其所具有的能量分布。VT和VF的频谱分布充分说明了信号具有非线性的特征。在图5和图6中我们利用相关维数和Lyapunov指数来研究心电信号的特征。相关维数和Lyapunov指数是非线性动力学发展中的动力学特征指标,在我们的研究中发现,VT和VF的相关维数呈分数维变化,并且VF的相关维数明显大于VT。Lyapunov指数的研究说明了心脏的非线性动力学特征,VT和VF计算的值相差不大,但VT和VF的Lyapunov指数都大于零,呈现出混沌特性。在图6中,我们计算了VT和VF的Lempel-Ziv复杂度,VT和VF各35条,其中代表VF信号,0代表VT信号,从计算出的复杂度对照图中看VF的复杂度明显的大于VT的复杂度(VF的复杂度的平均值为58,VT的复杂度的平均值为32);从复杂性动力学角度来看,VF的动力学行为更难以预测;在实验中,我们采集研究并发现心脏从窦性节律到心率过速,到心室纤颤,它们的平均复杂度基本上成倍数增长,在临床医学的心脏疾病的诊断中,我们可以建立复杂度阈值检测,为准确判断和及时的电击除颤提供一定的依据。从研究和仿真的结果可以表明:本多导联心电测量和分析系统具有良好的性能:多导联的数据采集程控性能高,上述虚拟仪器的控制灵活,非线性心电信号分析方法实用,VT和VF的分辨率高。在我们所测的心电数据下,VT与VF的识别率达到95%以上。本套虚拟多导联心电测试仪器在临床上具有广阔的前景。

, http://www.100md.com
图3 (a)VT时域信号

图4 (a)VT的频谱图

图3 (b)VF时域信号

图4 (b)VF的频谱图

图5 (a)VT信号的频谱幅度信息直方图

图5 (b)VF信号的频谱幅度信息直方图

, 百拇医药
图6 (a)VF的相关维数D2(m)与嵌入维数m函数关系图

图6 (b)心室纤颤节律下lgC2(r,m)~lgr

图7 VT和VF的Lyapunov指数图

图8 VT和VF复杂度对比图
基金项目:本课题承国家自然科学基金资助。
作者简介:张红煊(1972—),男,上海交通大学生物医学工程系博士研究生。
, 百拇医药
参考文献
[1] 张开滋,刘海洋,吴杰.心电信息学.第一版.科学技术文献出版社,1998,pp.3-45
[2] Takens F. Detecting strange attractors in turbulence. In:Rand DA, Young LS (eds),Dynamical system and turbulence, lecture notes in mathematics, Springer, Berlin,1981,898:366-387
[3] 张绪省.心室纤颤动力学特性的非线性分析及应用研究.上海交通大学博士论文,1997
[4] Zhang Xusheng, Zhu Yisheng. New approach to studies on ECG dynamics:extraction and analyses of QRS complex irregularity tome series. Medical & Biological Engineering & Computing,1997,pp.467-473
, 百拇医药
[5] Radhakrishnan N, Gangadhar BN. Estimating regularity in epileptic seizure time-series data. IEEE Engineering in Medicine and Biology,1998,pp.89-94
[6] 谢惠民.复杂性与动力系统.第一版,1994,pp.186-211
[7] Starrobin JM, Wgarton JM, Shander GS. Comparative analysis of polymorphic ventricular tachyarrhymias and fibrillation:clinical observations and numerical experiments. Computer in Cardiology,1998,25:25~28
[8] Zhang Xusheng, Zhu Yisheng, Thakor NV. Detecting ventricular tachycardia and fibrillation by complexity measure. IEEE Trans Biomed Eng,1999,46(5):548-555
(1999-10-20收稿), http://www.100md.com