近似熵和复杂度应用于睡眠脑电研究的比较*
作者：董国亚 吴祈耀
单位：北京理工大学 (100081)
关键词：近似熵(ApEn) 复杂度；睡眠脑电；REM；NREM
中国医疗器械杂志990601 提要 介绍了两种度量序列复杂性的方法，一种是Kaspar和Sch uster定义的复杂度算法，一种是最近新发展起来的度量序列复杂性的统计方法--近似熵(ApEn)。应用这两种方法对睡眠脑电各睡眠期提取复杂性的特征，并通过对比研究表明：近似熵是值得重视的、很有前景的复杂度度量方法。
The Comparison Between Approximate Entropy and Complexity in the Study of Sleep EEG
Dong Guoya Wu Qiyao
, 百拇医药
Beijing University of Science and Technolongy
ABSTRACT The Paper introduces tw o algorithms as a complexit y measure.One is the algorithm defined by Kaspar and Schuster,the other is a re cently developed statistic quantifying regularity and complexity--Approximate entropy(ApEn).They have been applied for the study of sleep EEG.According to the lab oratory application and comparison,the result shows that ApEn is a valued comple xity measure.
, 百拇医药
KEY WORDS Approximate Entropy ( ApEn) Complexity Sleep EEG REM NREM
一门新兴的边缘横断学科--睡眠医学(Sleep Medicine)已成为现代医学的一个重要组成部分正在建立和发展起来。
睡眠是一种重要的生理现象。睡眠对呼吸有直接的影响。由于神经系统驱动及对外界刺激反应减低，基础代谢下降，脑血流量增加，胸腹部活动下降，功能残气减低及呼吸气流增加等因素的影响，在NREM与REM睡眠时可对呼吸产生不同的影响。此外，睡眠时还出现肺泡通气量下降。睡眠时高碳酸血症对肺通气量的反应已有广泛的研究。醒觉时CO2的反应斜率为0.007～0.037L.min-1kPa-1(1～5L→min-1→mmHg-1)，NREM睡眠时下降53%，REM睡眠时下降28%～75%。吸入CO2引起通气量增加的机械性刺激，对睡眠时引起觉醒反应有作用。由上可看出，在睡眠的不同阶段对呼吸的影响也不同。有些潜在于身体中的疾病，特别是大脑的疾病，在清醒状态下病灶不容易被发觉。睡眠时，由于大脑对外界刺激的反应减少，这样就会使其显露出来，而且在不同的睡眠阶段显露的程度不同。所以对睡眠的生理及病理作一些基础性研究对睡眠障碍及其有关疾患，对睡眠呼吸障碍与系统性疾患关系的了解以及诊治是有益处的。研究睡眠分期，对疾病的检测、预防和治疗有重要的临床意义。
, http://www.100md.com
脑电图是一项常规的临床检查项目，它在脑功能评估方面的作用是任何其它评估方法不可替代的。在睡眠及睡眠的研究过程中，脑电图一直是重要且有力的工具。传统的EEG分析方法有：以分析EEG波形的几何性质，如幅度、均值、峭度等为主的时域分析方法和以分析EEG功率谱、相干函数等为主的频域方法。传统的分析方法用于研究睡眠脑电已取得了一定的成果。实践表明，应用传统的分析方法分析睡眠期的脑电活动，存在较大的局限性，提取的信息有限，难以完全满足临床的要求。近年来随着非线性系统分析理论的发展及其在生物医学中的应用，促进了睡眠脑电的进一步研究，如相关维数、Lyapunov指数、复杂性测度等。其中复杂性测度的方法目前还没有统一的算法，本文介绍两种度量序列复杂性的算法，一种是Kaspar和Schuster定义的复杂性测度的算法，一种是最近发展起来的度量系统复杂性的统计方法--近似熵。通过实验、研究、对比表明：近似熵是值得重视的、很有前景的复杂度度量方法。
1. 定义及算法
事物的复杂性既有空间结构上的复杂性，又有随时间变化上的复杂性。70年代Lem-Ziv在信息理论的研究中对随机序列的复杂性给出了一定义，认为复杂性反映了一个时间序列随其长度的增长出现新模式的速率，表现了序列接近随机的程度。Kormogrov对复杂性的研究认为，复杂性就是产生给定“0，1”序列所需最少的计算机程序的比特数。一般认为描述事物的计算机语言的长度越长，则认为该事物越复杂。
, 百拇医药
脑电序列的复杂性表现了EEG序列的随机程度，反映了决定这段EEG序列的信息量的大小。从实验和分析来看，EEG序列的复杂性表示了大脑神经元处理信息活动的有序程度。
1.1 复杂度的定义及算法
80年代末期，Kasper和Schuster对于随机序列复杂性测度的算法进行了研究，并提出了随机序列复杂性测度的算法。对于复杂性测度没有一般的算法，这里就Kasper和Schuster的算法进行描述。
要处理EEG时间序列S(S1，S2，…，Sn)，首先对它进行粗粒化处理。先求序列的平均值，然后根据Si大于平均值时S'i＝1，Si小于平均值时S'i＝0的规则重构序列S'(S'1，S'2，…，S'n)。不妨也设重构序列为S(S1，S2，…，Sn)。对重构序列形成的(0，1)字符串按一定的规则进行划分子串界定。
, 百拇医药
对于一个字符串S(S1，S2，…，Sn)后再加一个字符串Q(q1，q2，…，qn)得到一个字符串SQ，令SQv是SQ减去最后一个字符所得字符串，再判断Q是否是SQv的一个子串，如果Q是SQv的一个子串，把这个字符加到后面，继续增长Q，再判断。如果Q不是SQv的一个子串，则用“.”把前后分开，下一步把“.”前的所有字符看成S，重新构造Q，重复以上过程直到结束。序列的复杂性定义为由“.”界定的S的子串数目。例如01001的复杂度可由下列步骤计算：
1. 第一个字符总是插入 →0.
2. S＝0，Q＝1，SQ＝01，SQv＝0，QSQv →0.1.
3. S＝01，Q＝0，SQ＝010，SQv＝01，Q∈SQv →0.1.0
, http://www.100md.com
4. S＝01，Q＝00，SQ＝0100，SQv＝010，QSQv →0.1.00.
5. S＝0100，Q＝1，SQ＝01001，SQv＝0100，Q∈SQv →0.1.00.1
这个序列复杂度c(n)＝4，即c(01001)＝4。
Lempel和Ziv对Si属于[0，1]的序列进行了研究，几乎所有的c(n)都趋向于一定值。即：
limn→∞c(n)＝b(n)＝n/logn
所以c(n)是随机序列的渐近行为。可以用b(n)来对c(n)进行归一化。即：
C(n)＝c(n)/b(n)
, http://www.100md.com
我们就是用这归一化的C(n)来测度时间序列的复杂性变化，对完全随机的序列C(n)值趋向于1，而周期性序列的C(n)趋向于0，其余情况介于两者之间。相对复杂度C(n)反应了一个时间序列与随机序列的接近程度，某序列的C(n)趋向于1，则表明这个序列趋近随机序列。
1.2 近似熵的定义及算法
近似熵(Approximate entropy,简称ApEn)是最近发展起来的由Pincus在1991年提出的一种度量序列的复杂性和统计量化的规则。它对于相对较短的(大于100个数据点)、含噪声的时间序列显示出潜在的应用价值，这是因为产生近似熵的主要的技术思想就是：它并不是企图完全重构吸引子，而是用一种有效的统计方式--边缘概率的分布来区分各种过程。在应用的过程中，近似熵表现出以下主要的特点：
(1) 只需要比较短的数据就能估计出比较稳定的统计值。所需的数据点大致在100～5000点，一般在1000点左右。
, http://www.100md.com
(2) 有较好的抗干扰和抗噪的能力。
(3) 对于随机信号或是确定性信号都可以使用，也可以应用于由随机成分和确定性成分混合的信号。
(4) 尤其对分析生物系统是有利的。
计算近似熵时，输入两个参数m,r且在整个计算过程中固定不变。m是比较序列的长度，即窗口长度，r是一个有效的阈值。给出N个点u(1)，u(2)，…，u(N)，对固定的m和r定义两个参数，一个是极限值ApEn(m,r)，一个是这N个点的统计估计值ApEn(m,r,N)。下面结合算法步骤来说明近似熵的定义。
1) 设原始数据为u(1)，u(2)，…，u(N)共N个点。
2) 按序号连续顺序组成一组m维矢量：从X(1)到X(N-m+1),其中：X(i)＝[u(i)，u(i+1)，…，u(i+m-1)]。i＝1～N-m+1。这些矢量代表着从第i个点开始的连续m个u值。
, http://www.100md.com
3) 定义矢量X(i)和X(j)间的距离d[X(i)，X(j)]为两者对应元素中差值最大的一个，即：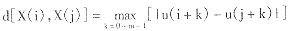
(此时X(i)，X(j)中其他对应元素间差值自然都小于d)。并对每一个i值计算X(i)与其余矢量X(j)(j=1～N-m+1,但j≠i)间的距离d[X(i),X(j)]。
4) 给定阈值r，对每个i≤N-m+1的值，统计d[X(i),X(j)]小于r的数目及此数目与距离总数N-m的比值，记作Cmi(r)。即：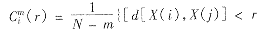
的数目}i＝1～N-m+1
5) 先将Cmi(r)取对数，再求其对所有i的平均值，记作φm(r)。即：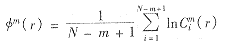
, 百拇医药
6) 再把维数加1，变成m+1，重复步骤2-5，得Cm+1i(r)和φm+1(r)。
7) 理论上此序列的近似熵为：
一般言之，此极限值以概率1存在。实际工作时N不可能为∞。当N为有限值时按上述步骤得出的是序列长度为N时ApEn的估计值。记作：
ApEn的值显然与m，r的取值有关。Pincus根据实践，建议取m＝2，r＝0.1～0.2SD[SD是原始数据u(i),i=1～N的标准差(standard deviation)]。
2. 二者应用于睡眠脑电研究的实验结果对比
, 百拇医药
2.1 实验的环境条件：
2.1.1 本项研究所具备的实验数据的条件
本实验的所有睡眠数据都是在医院中由医生对被测试者进行8小时的睡眠监测而采集的，并且经过去噪后而得到的脑电数据。但是其中仍有一些在睡眠过程中由于被测试者改变体位或呼吸障碍等因素而带来的干扰。所有睡眠数据都经过经验丰富的医生进行了人工的睡眠分期，以此分期结果作为研究各睡眠期特征的参考标准。
2.1.2 被测试者脑电数据简介
(1) 被测试者7071和7072：整个睡眠过程中没有深度睡眠Ⅲ、Ⅳ期阶段，由于存在呼吸障碍而导致呼吸事件使睡眠EEG中的干扰较多；
(2) 被测试者7081和7082：由于睡眠较好，所以有睡眠Ⅲ、Ⅳ期阶段，且睡眠过程中呼吸正常，没有呼吸事件，但Ⅳ期经历的时间又比较短，睡眠深度还不够。
, http://www.100md.com
(3) 被测试者7091和7092：在睡眠过程中有许多呼吸障碍而导致的呼吸事件，所以脑电EEG中干扰也较多，没有进入Ⅲ、Ⅳ期睡眠；
2.1.3 软硬件环境
此程序是在486微机，Windows3.1环境下运用Borland C++4.5编写的Windows程序。
2.2 实验结果对比
复杂度的实验结果见表1，近似熵的实验结果见表2。
表1：
睡眠各期的复杂度(平均值) 受测试者
导联数
Wake期
, 百拇医药
NREM期
REM期
Ⅰ期
Ⅱ期
Ⅲ期
Ⅳ期
7071
C3-A1
C4-A2
0.1373
0.1607
0.1336
0.1506
, 百拇医药
0.1175
0.1326----
0.1191
0.1385
7072
C3-A1
C4-A2
0.1520
0.1829
0.1327
0.1482
0.1220
, http://www.100md.com 0.1394----
0.1173
0.1367
7081
C3-A1
C4-A2
0.2015
0.2105
0.1709
0.1878
0.1091
0.1226
0.0826
, 百拇医药
0.0939
0.0860
0.1007
0.1463
0.1663
7082
C3-A1
C4-A2
0.1923
0.2113
0.1375
0.1472
, 百拇医药 0.1267
0.1380
0.0952
0.1011
0.0860
0.1380
0.1416
0.1631
7091
C3-A1
C4-A2
0.1471
0.1612
, 百拇医药
0.1560
0.1611
0.1014
0.0780----
0.1555
0.1581
7092
C3-A1
C4-A2
0.1628
0.1625
0.1318
, http://www.100md.com 0.1439
0.1149
0.0881----
0.1146
0.1151
表2：睡眠各期的ApEn(平均值) 受测试者
导联数
Wake期
NREM期
REM期
Ⅰ期
Ⅱ期
, 百拇医药 Ⅲ期
Ⅳ期
7071
C3-A1
C4-A2
0.863
0.970
0.777
0.847
0.644
0.754----
0.736
0.842
, 百拇医药
7072
C3-A1
C4-A2
0.963
1.047
0.794
0.866
0.716
0.796----
0.726
0.836
7081
C3-A1
, 百拇医药
C4-A2
1.028
1.062
0.918
0.979
0.639
0.689
0.520
0.584
0.525
0.583
0.872
0.961
, 百拇医药
7082
C3-A1
C4-A2
0.969
1.045
0.808
0.835
0.706
0.755
0.552
0.594
0.526
0.577
, 百拇医药
0.855
0.945
7091
C3-A1
C4-A2
0.905
1.009
0.833
0.720
0.645
0.531----
0.781
0.799
, 百拇医药
7092
C3-A1
C4-A2
1.015
1.037
0.828
0.943
0.686
0.597----
0.738
0.779
通过上面的实验结果可以看出，对于各睡眠期应用两种方法提取出的特征具有相同的变化规律，但是一个显著的不同就是提取出的近似熵的幅度明显大于复杂度的幅度，现将提取出的各睡眠期的规律总结如下：
, 百拇医药
(1) 由以8～13次/秒节律的α波为主的Wake期→α波逐渐减弱，出现慢波的Ⅰ期→α波出现自动调幅产生梭波的Ⅱ期的过程中，大脑的思维活动逐渐减少；ApEn和复杂度的值也由Wake期的最大而逐步递减。
(2) 以梭波为主，夹有“K”波的Ⅱ期→梭波显著减少，取而代之的是波幅增高、频率减小的δ波逐渐增加的Ⅲ期、Ⅳ期的过程中，大脑思维活动进一步显著减少，进入深度睡眠；ApEn和复杂度的值与Ⅱ期相比也进一步递减。
(3) 到REM期，EEG又与觉醒或Ⅰ期时的相仿，此时虽依然处于深睡，但大脑又恢复一定的思维活动，80%做梦。ApEn和复杂度也由Ⅲ、Ⅳ期的最低点回升到与Ⅰ期或Ⅱ期接近。
(4) 对于Ⅲ、Ⅳ期之间比较ApEn和复杂度，它们的ApEn和复杂度的值都低于睡眠的其它各期，就EEG来讲，Ⅲ、Ⅳ都以δ波为特征。不同的是Ⅲ期的δ波超过20%，但不超过50%。而Ⅳ期的δ波超过50%且波幅更高，频率更慢。通过对Ⅲ、Ⅳ期的典型特征波的分析来看，Ⅲ期的ApEn和复杂度>Ⅳ期的ApEn和复杂度，但通过平均的ApEn和复杂度值及曲线图来看，两者相差无几，非常接近。
, 百拇医药
(5) 睡眠正常，没有呼吸事件的睡眠脑电所计算出的ApEn值>有呼吸事件的睡眠脑电所计算出的ApEn值。
2.2 曲线对比
图1
通过截取下ApEn的曲线和复杂度的曲线，可以看出这两者的变化规律基本相同，这也说明了两种算法反映了序列相同变化特点即：序列复杂性的变化特点，进一步证明了近似熵也是测量序列的复杂性的一种方法，显著不同的是ApEn曲线的幅值明显的高于复杂度曲线的幅值。这也说明了近似熵能更多地提取出序列的复杂性信息。因为它是从多维的角度来计算序列的复杂性，包含了时间模式的信息。
3.0 总结
通过以上两种方法计算的结果及表现出的规律，总结出以下异同点：
, 百拇医药
1.性质：复杂度和近似熵都是度量数据序列的复杂性的一种方法。
2.物理意义：复杂度只是从一维即m=1的角度反映了时间序列随其长度的增长而出现新模式的速率，丢失了数据蕴含在时间序列中的信息。而近似熵是当维数m由2增至3时产生新模式可能性的大小，包含了时间模式的信息，反映时间新模式发生率随维数而增减的情况。因而反映了数据在结构上的复杂性，包含有更多的信息。
这就是虽然变化规律相同，但近似熵的幅值明显大于复杂度且比复杂度的变化规律更明显的缘故。
3.计算结果：两者计算出的数据具有相同的变化规律，即从清醒到NREM期的Ⅲ、Ⅳ期，ApEn值和C(n)值都是由最大依此减小，到REM期又回升到接近Ⅰ和Ⅱ期，但ApEn值远大于C(n)值。这说明ApEn值中包含有系统更多的信息，也是由它的物理意义决定的。
4 曲线规律：曲线的变化规律相同，但ApEn的幅值要明显得高于复杂度的幅值，进而使变化规律更加明显，能更好地区分各睡眠期的特点。
, http://www.100md.com
5 程序的计算速度：由于两种算法公式决定了计算机编码的长度和运算速度。由于每计算一个值，每个窗口长度的矢量都要与其它(N-m)个相同窗口长度的矢量进行比较计算，且至少要循环[(N-m)+1]*(N-m)/2次，所以计算速度比较慢，这也是将运用于临床所急需解决的问题。相反计算复杂度所需的时间要短很多。8小时的脑电，计算一导的ApEn值需将近四个小时，而计算复杂度只需几分钟的时间，这是复杂度的一个很大的优势。
*本课题获卫生部科学研究基金96-2-276资助
参考文献
1 杨福生等.近似熵：一种适用于短数据的复杂性度量.中国医疗器械杂志.1997；21(5)：283-286
2 S.M.Pincus.Approximate entropy(ApEn)as a complexity meas ure Chaos 1995;5(1)：110-117
3 S.M.Pincus.Approximate entropy as a measure of system complexity .Proc.Natl.Acad.Sci,1991;88：2297-2301
4 刘建平等.不同睡眠期脑电图复杂性研究.生物医学工程学杂志.1996；13(2)：119-122
(1998年12月9日收稿), 百拇医药
单位：北京理工大学 (100081)
关键词：近似熵(ApEn) 复杂度；睡眠脑电；REM；NREM
中国医疗器械杂志990601 提要 介绍了两种度量序列复杂性的方法，一种是Kaspar和Sch uster定义的复杂度算法，一种是最近新发展起来的度量序列复杂性的统计方法--近似熵(ApEn)。应用这两种方法对睡眠脑电各睡眠期提取复杂性的特征，并通过对比研究表明：近似熵是值得重视的、很有前景的复杂度度量方法。
The Comparison Between Approximate Entropy and Complexity in the Study of Sleep EEG
Dong Guoya Wu Qiyao
, 百拇医药
Beijing University of Science and Technolongy
ABSTRACT The Paper introduces tw o algorithms as a complexit y measure.One is the algorithm defined by Kaspar and Schuster,the other is a re cently developed statistic quantifying regularity and complexity--Approximate entropy(ApEn).They have been applied for the study of sleep EEG.According to the lab oratory application and comparison,the result shows that ApEn is a valued comple xity measure.
, 百拇医药
KEY WORDS Approximate Entropy ( ApEn) Complexity Sleep EEG REM NREM
一门新兴的边缘横断学科--睡眠医学(Sleep Medicine)已成为现代医学的一个重要组成部分正在建立和发展起来。
睡眠是一种重要的生理现象。睡眠对呼吸有直接的影响。由于神经系统驱动及对外界刺激反应减低，基础代谢下降，脑血流量增加，胸腹部活动下降，功能残气减低及呼吸气流增加等因素的影响，在NREM与REM睡眠时可对呼吸产生不同的影响。此外，睡眠时还出现肺泡通气量下降。睡眠时高碳酸血症对肺通气量的反应已有广泛的研究。醒觉时CO2的反应斜率为0.007～0.037L.min-1kPa-1(1～5L→min-1→mmHg-1)，NREM睡眠时下降53%，REM睡眠时下降28%～75%。吸入CO2引起通气量增加的机械性刺激，对睡眠时引起觉醒反应有作用。由上可看出，在睡眠的不同阶段对呼吸的影响也不同。有些潜在于身体中的疾病，特别是大脑的疾病，在清醒状态下病灶不容易被发觉。睡眠时，由于大脑对外界刺激的反应减少，这样就会使其显露出来，而且在不同的睡眠阶段显露的程度不同。所以对睡眠的生理及病理作一些基础性研究对睡眠障碍及其有关疾患，对睡眠呼吸障碍与系统性疾患关系的了解以及诊治是有益处的。研究睡眠分期，对疾病的检测、预防和治疗有重要的临床意义。
, http://www.100md.com
脑电图是一项常规的临床检查项目，它在脑功能评估方面的作用是任何其它评估方法不可替代的。在睡眠及睡眠的研究过程中，脑电图一直是重要且有力的工具。传统的EEG分析方法有：以分析EEG波形的几何性质，如幅度、均值、峭度等为主的时域分析方法和以分析EEG功率谱、相干函数等为主的频域方法。传统的分析方法用于研究睡眠脑电已取得了一定的成果。实践表明，应用传统的分析方法分析睡眠期的脑电活动，存在较大的局限性，提取的信息有限，难以完全满足临床的要求。近年来随着非线性系统分析理论的发展及其在生物医学中的应用，促进了睡眠脑电的进一步研究，如相关维数、Lyapunov指数、复杂性测度等。其中复杂性测度的方法目前还没有统一的算法，本文介绍两种度量序列复杂性的算法，一种是Kaspar和Schuster定义的复杂性测度的算法，一种是最近发展起来的度量系统复杂性的统计方法--近似熵。通过实验、研究、对比表明：近似熵是值得重视的、很有前景的复杂度度量方法。
1. 定义及算法
事物的复杂性既有空间结构上的复杂性，又有随时间变化上的复杂性。70年代Lem-Ziv在信息理论的研究中对随机序列的复杂性给出了一定义，认为复杂性反映了一个时间序列随其长度的增长出现新模式的速率，表现了序列接近随机的程度。Kormogrov对复杂性的研究认为，复杂性就是产生给定“0，1”序列所需最少的计算机程序的比特数。一般认为描述事物的计算机语言的长度越长，则认为该事物越复杂。
, 百拇医药
脑电序列的复杂性表现了EEG序列的随机程度，反映了决定这段EEG序列的信息量的大小。从实验和分析来看，EEG序列的复杂性表示了大脑神经元处理信息活动的有序程度。
1.1 复杂度的定义及算法
80年代末期，Kasper和Schuster对于随机序列复杂性测度的算法进行了研究，并提出了随机序列复杂性测度的算法。对于复杂性测度没有一般的算法，这里就Kasper和Schuster的算法进行描述。
要处理EEG时间序列S(S1，S2，…，Sn)，首先对它进行粗粒化处理。先求序列的平均值，然后根据Si大于平均值时S'i＝1，Si小于平均值时S'i＝0的规则重构序列S'(S'1，S'2，…，S'n)。不妨也设重构序列为S(S1，S2，…，Sn)。对重构序列形成的(0，1)字符串按一定的规则进行划分子串界定。
, 百拇医药
对于一个字符串S(S1，S2，…，Sn)后再加一个字符串Q(q1，q2，…，qn)得到一个字符串SQ，令SQv是SQ减去最后一个字符所得字符串，再判断Q是否是SQv的一个子串，如果Q是SQv的一个子串，把这个字符加到后面，继续增长Q，再判断。如果Q不是SQv的一个子串，则用“.”把前后分开，下一步把“.”前的所有字符看成S，重新构造Q，重复以上过程直到结束。序列的复杂性定义为由“.”界定的S的子串数目。例如01001的复杂度可由下列步骤计算：
1. 第一个字符总是插入 →0.
2. S＝0，Q＝1，SQ＝01，SQv＝0，QSQv →0.1.
3. S＝01，Q＝0，SQ＝010，SQv＝01，Q∈SQv →0.1.0
, http://www.100md.com
4. S＝01，Q＝00，SQ＝0100，SQv＝010，QSQv →0.1.00.
5. S＝0100，Q＝1，SQ＝01001，SQv＝0100，Q∈SQv →0.1.00.1
这个序列复杂度c(n)＝4，即c(01001)＝4。
Lempel和Ziv对Si属于[0，1]的序列进行了研究，几乎所有的c(n)都趋向于一定值。即：
limn→∞c(n)＝b(n)＝n/logn
所以c(n)是随机序列的渐近行为。可以用b(n)来对c(n)进行归一化。即：
C(n)＝c(n)/b(n)
, http://www.100md.com
我们就是用这归一化的C(n)来测度时间序列的复杂性变化，对完全随机的序列C(n)值趋向于1，而周期性序列的C(n)趋向于0，其余情况介于两者之间。相对复杂度C(n)反应了一个时间序列与随机序列的接近程度，某序列的C(n)趋向于1，则表明这个序列趋近随机序列。
1.2 近似熵的定义及算法
近似熵(Approximate entropy,简称ApEn)是最近发展起来的由Pincus在1991年提出的一种度量序列的复杂性和统计量化的规则。它对于相对较短的(大于100个数据点)、含噪声的时间序列显示出潜在的应用价值，这是因为产生近似熵的主要的技术思想就是：它并不是企图完全重构吸引子，而是用一种有效的统计方式--边缘概率的分布来区分各种过程。在应用的过程中，近似熵表现出以下主要的特点：
(1) 只需要比较短的数据就能估计出比较稳定的统计值。所需的数据点大致在100～5000点，一般在1000点左右。
, http://www.100md.com
(2) 有较好的抗干扰和抗噪的能力。
(3) 对于随机信号或是确定性信号都可以使用，也可以应用于由随机成分和确定性成分混合的信号。
(4) 尤其对分析生物系统是有利的。
计算近似熵时，输入两个参数m,r且在整个计算过程中固定不变。m是比较序列的长度，即窗口长度，r是一个有效的阈值。给出N个点u(1)，u(2)，…，u(N)，对固定的m和r定义两个参数，一个是极限值ApEn(m,r)，一个是这N个点的统计估计值ApEn(m,r,N)。下面结合算法步骤来说明近似熵的定义。
1) 设原始数据为u(1)，u(2)，…，u(N)共N个点。
2) 按序号连续顺序组成一组m维矢量：从X(1)到X(N-m+1),其中：X(i)＝[u(i)，u(i+1)，…，u(i+m-1)]。i＝1～N-m+1。这些矢量代表着从第i个点开始的连续m个u值。
, http://www.100md.com
3) 定义矢量X(i)和X(j)间的距离d[X(i)，X(j)]为两者对应元素中差值最大的一个，即：
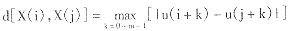
(此时X(i)，X(j)中其他对应元素间差值自然都小于d)。并对每一个i值计算X(i)与其余矢量X(j)(j=1～N-m+1,但j≠i)间的距离d[X(i),X(j)]。
4) 给定阈值r，对每个i≤N-m+1的值，统计d[X(i),X(j)]小于r的数目及此数目与距离总数N-m的比值，记作Cmi(r)。即：
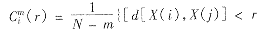的数目}i＝1～N-m+15) 先将Cmi(r)取对数，再求其对所有i的平均值，记作φm(r)。即：
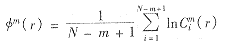
, 百拇医药
6) 再把维数加1，变成m+1，重复步骤2-5，得Cm+1i(r)和φm+1(r)。
7) 理论上此序列的近似熵为：
一般言之，此极限值以概率1存在。实际工作时N不可能为∞。当N为有限值时按上述步骤得出的是序列长度为N时ApEn的估计值。记作：
ApEn的值显然与m，r的取值有关。Pincus根据实践，建议取m＝2，r＝0.1～0.2SD[SD是原始数据u(i),i=1～N的标准差(standard deviation)]。
2. 二者应用于睡眠脑电研究的实验结果对比
, 百拇医药
2.1 实验的环境条件：
2.1.1 本项研究所具备的实验数据的条件
本实验的所有睡眠数据都是在医院中由医生对被测试者进行8小时的睡眠监测而采集的，并且经过去噪后而得到的脑电数据。但是其中仍有一些在睡眠过程中由于被测试者改变体位或呼吸障碍等因素而带来的干扰。所有睡眠数据都经过经验丰富的医生进行了人工的睡眠分期，以此分期结果作为研究各睡眠期特征的参考标准。
2.1.2 被测试者脑电数据简介
(1) 被测试者7071和7072：整个睡眠过程中没有深度睡眠Ⅲ、Ⅳ期阶段，由于存在呼吸障碍而导致呼吸事件使睡眠EEG中的干扰较多；
(2) 被测试者7081和7082：由于睡眠较好，所以有睡眠Ⅲ、Ⅳ期阶段，且睡眠过程中呼吸正常，没有呼吸事件，但Ⅳ期经历的时间又比较短，睡眠深度还不够。
, http://www.100md.com
(3) 被测试者7091和7092：在睡眠过程中有许多呼吸障碍而导致的呼吸事件，所以脑电EEG中干扰也较多，没有进入Ⅲ、Ⅳ期睡眠；
2.1.3 软硬件环境
此程序是在486微机，Windows3.1环境下运用Borland C++4.5编写的Windows程序。
2.2 实验结果对比
复杂度的实验结果见表1，近似熵的实验结果见表2。
表1：
睡眠各期的复杂度(平均值) 受测试者
导联数
Wake期
, 百拇医药
NREM期
REM期
Ⅰ期
Ⅱ期
Ⅲ期
Ⅳ期
7071
C3-A1
C4-A2
0.1373
0.1607
0.1336
0.1506
, 百拇医药
0.1175
0.1326----
0.1191
0.1385
7072
C3-A1
C4-A2
0.1520
0.1829
0.1327
0.1482
0.1220
, http://www.100md.com 0.1394----
0.1173
0.1367
7081
C3-A1
C4-A2
0.2015
0.2105
0.1709
0.1878
0.1091
0.1226
0.0826
, 百拇医药
0.0939
0.0860
0.1007
0.1463
0.1663
7082
C3-A1
C4-A2
0.1923
0.2113
0.1375
0.1472
, 百拇医药 0.1267
0.1380
0.0952
0.1011
0.0860
0.1380
0.1416
0.1631
7091
C3-A1
C4-A2
0.1471
0.1612
, 百拇医药
0.1560
0.1611
0.1014
0.0780----
0.1555
0.1581
7092
C3-A1
C4-A2
0.1628
0.1625
0.1318
, http://www.100md.com 0.1439
0.1149
0.0881----
0.1146
0.1151
表2：睡眠各期的ApEn(平均值) 受测试者
导联数
Wake期
NREM期
REM期
Ⅰ期
Ⅱ期
, 百拇医药 Ⅲ期
Ⅳ期
7071
C3-A1
C4-A2
0.863
0.970
0.777
0.847
0.644
0.754----
0.736
0.842
, 百拇医药
7072
C3-A1
C4-A2
0.963
1.047
0.794
0.866
0.716
0.796----
0.726
0.836
7081
C3-A1
, 百拇医药
C4-A2
1.028
1.062
0.918
0.979
0.639
0.689
0.520
0.584
0.525
0.583
0.872
0.961
, 百拇医药
7082
C3-A1
C4-A2
0.969
1.045
0.808
0.835
0.706
0.755
0.552
0.594
0.526
0.577
, 百拇医药
0.855
0.945
7091
C3-A1
C4-A2
0.905
1.009
0.833
0.720
0.645
0.531----
0.781
0.799
, 百拇医药
7092
C3-A1
C4-A2
1.015
1.037
0.828
0.943
0.686
0.597----
0.738
0.779
通过上面的实验结果可以看出，对于各睡眠期应用两种方法提取出的特征具有相同的变化规律，但是一个显著的不同就是提取出的近似熵的幅度明显大于复杂度的幅度，现将提取出的各睡眠期的规律总结如下：
, 百拇医药
(1) 由以8～13次/秒节律的α波为主的Wake期→α波逐渐减弱，出现慢波的Ⅰ期→α波出现自动调幅产生梭波的Ⅱ期的过程中，大脑的思维活动逐渐减少；ApEn和复杂度的值也由Wake期的最大而逐步递减。
(2) 以梭波为主，夹有“K”波的Ⅱ期→梭波显著减少，取而代之的是波幅增高、频率减小的δ波逐渐增加的Ⅲ期、Ⅳ期的过程中，大脑思维活动进一步显著减少，进入深度睡眠；ApEn和复杂度的值与Ⅱ期相比也进一步递减。
(3) 到REM期，EEG又与觉醒或Ⅰ期时的相仿，此时虽依然处于深睡，但大脑又恢复一定的思维活动，80%做梦。ApEn和复杂度也由Ⅲ、Ⅳ期的最低点回升到与Ⅰ期或Ⅱ期接近。
(4) 对于Ⅲ、Ⅳ期之间比较ApEn和复杂度，它们的ApEn和复杂度的值都低于睡眠的其它各期，就EEG来讲，Ⅲ、Ⅳ都以δ波为特征。不同的是Ⅲ期的δ波超过20%，但不超过50%。而Ⅳ期的δ波超过50%且波幅更高，频率更慢。通过对Ⅲ、Ⅳ期的典型特征波的分析来看，Ⅲ期的ApEn和复杂度>Ⅳ期的ApEn和复杂度，但通过平均的ApEn和复杂度值及曲线图来看，两者相差无几，非常接近。
, 百拇医药
(5) 睡眠正常，没有呼吸事件的睡眠脑电所计算出的ApEn值>有呼吸事件的睡眠脑电所计算出的ApEn值。
2.2 曲线对比
图1
通过截取下ApEn的曲线和复杂度的曲线，可以看出这两者的变化规律基本相同，这也说明了两种算法反映了序列相同变化特点即：序列复杂性的变化特点，进一步证明了近似熵也是测量序列的复杂性的一种方法，显著不同的是ApEn曲线的幅值明显的高于复杂度曲线的幅值。这也说明了近似熵能更多地提取出序列的复杂性信息。因为它是从多维的角度来计算序列的复杂性，包含了时间模式的信息。
3.0 总结
通过以上两种方法计算的结果及表现出的规律，总结出以下异同点：
, 百拇医药
1.性质：复杂度和近似熵都是度量数据序列的复杂性的一种方法。
2.物理意义：复杂度只是从一维即m=1的角度反映了时间序列随其长度的增长而出现新模式的速率，丢失了数据蕴含在时间序列中的信息。而近似熵是当维数m由2增至3时产生新模式可能性的大小，包含了时间模式的信息，反映时间新模式发生率随维数而增减的情况。因而反映了数据在结构上的复杂性，包含有更多的信息。
这就是虽然变化规律相同，但近似熵的幅值明显大于复杂度且比复杂度的变化规律更明显的缘故。
3.计算结果：两者计算出的数据具有相同的变化规律，即从清醒到NREM期的Ⅲ、Ⅳ期，ApEn值和C(n)值都是由最大依此减小，到REM期又回升到接近Ⅰ和Ⅱ期，但ApEn值远大于C(n)值。这说明ApEn值中包含有系统更多的信息，也是由它的物理意义决定的。
4 曲线规律：曲线的变化规律相同，但ApEn的幅值要明显得高于复杂度的幅值，进而使变化规律更加明显，能更好地区分各睡眠期的特点。
, http://www.100md.com
5 程序的计算速度：由于两种算法公式决定了计算机编码的长度和运算速度。由于每计算一个值，每个窗口长度的矢量都要与其它(N-m)个相同窗口长度的矢量进行比较计算，且至少要循环[(N-m)+1]*(N-m)/2次，所以计算速度比较慢，这也是将运用于临床所急需解决的问题。相反计算复杂度所需的时间要短很多。8小时的脑电，计算一导的ApEn值需将近四个小时，而计算复杂度只需几分钟的时间，这是复杂度的一个很大的优势。
*本课题获卫生部科学研究基金96-2-276资助
参考文献
1 杨福生等.近似熵：一种适用于短数据的复杂性度量.中国医疗器械杂志.1997；21(5)：283-286
2 S.M.Pincus.Approximate entropy(ApEn)as a complexity meas ure Chaos 1995;5(1)：110-117
3 S.M.Pincus.Approximate entropy as a measure of system complexity .Proc.Natl.Acad.Sci,1991;88：2297-2301
4 刘建平等.不同睡眠期脑电图复杂性研究.生物医学工程学杂志.1996；13(2)：119-122
(1998年12月9日收稿), 百拇医药