肾脏彩色血流信号定量的新方法
作者:李振彩 高云华
单位:李振彩(100037 北京解放军第304医院超声科);高云华(重庆市第三军医大学新桥医院超声科)
关键词:分形;分数维;肾脏;彩色多普勒血流图;兔;环孢素A
中国超声医学杂志991003
摘 要 目的:1.判断兔肾脏CDFI是否具有分形特征并探讨该定量方法的实际应用价值;2.研究环孢素A(CsA)对兔肾脏血流的影响。方法:选用体重(1.75kg~1.80kg)相当的雄性新西兰大白兔6只,每天静脉注射CsA 15mg/kg共21天,然后用彩色多普勒观察肾内的血流变化。采用数格子法对用药前、后肾内血流信号进行定量。结果:用药前、后肾脏彩色血流的分数维平均值分别为1.90±0.05和1.51±0.04,均大于其拓扑维数(Dt=1),这说明肾血管树具有分形结构。用药后肾脏CDFI的分数维值明显小于用药前。结论:1.肾脏的CDFI具有分形特征并可用分数维进行定量计算;2.CsA能够引起肾内血流信号的减少。
, http://www.100md.com
A New Quantitative Method of the Renal Color Doppler Flow Signals
Li Zhencai,Gao Yunhua
PLA 304 Hospital,Beijing 100037
ABSTRACT Objective:The aims of this paper are:1.To determine whether the rabbit renal color Doppler flow imaging(CDFI)has a fractal structure and to discuss the practicality of this quantitative methed;2.To assess the effect of Cyclosporine A(CsA)on the intrarenal blood flow of rabbit kidneys.Methods:CsA was administered intravenously for 21 days at doses of 15 mg/kg/d to six male New Zealand White rabbits(weighting 1.75~1.80kg).Then,the intrarenal blood flow was assessed by color Doppler ultrasound.The fractal dimensions of renal CDFI were calculated using an implementation of the box-counting method on an imaging analysis system before and after drug administration.Results:Before and after drug administration,the mean fractal dimensions were 1.90±0.05 and 1.51±0.04 respectively,which were significantly greater than its topological dimension(Dt=1),indicating that the renal CDFI has a fractal structure.After the drug administration the fractal dimensions were significantly less then the before drug administrations.Conclusion:1.The CDFI of the kidney has a fractal structure and can be measured by fractal dimension.2.CsA can reduce the renal color Doppler signals.
, http://www.100md.com
KEY WORDS Fractals Fractal Dimension Kidney Color Doppler fLow imaging Rabbit Cyclosporine A
由于肾脏彩色血流信号不规则也没有特定的几何形状,我们很难用传统的几何学方法进行定量。以前的研究多采用定性或半定量的方法〔1,2〕,但不能反应血流信号的细微变化。为此,本文的主要目的是(1).判断肾脏彩色血流图像(CDFI)是否具有分形特征并探讨该定量方法的实际应用价值;(2)研究环孢素A(CsA)对兔肾脏血流的影响。
资料与方法
选用体重(1.75kg~1.80kg)相当的雄性新西兰大白兔6只,每天静脉注射CsA 15mg/kg,注射前用生理盐水将CsA稀释为1ml,整个实验过程共21天。超声检查时间分别为用药前和用药后第21天,每次超声检查时用3%的戊巴比妥钠30mg/kg麻醉动物(静脉注射),然后用探头反复扫查双侧肾脏,尽量获得经过肾门的最大冠状切面,用彩色多普勒观察肾内的血流状况,调节彩色多普勒增益并尽量消除背景噪声,条件设置如下:彩色增益85%、壁滤波50、彩色血流最低流速3.0cm/s。最后记录彩色多普勒血流图像。仪器:采用ATL HDI型超9(ultramark 9)彩色多普勒超声仪,探头频率5.0~10.0MHz。
, http://www.100md.com
计算方法:肾脏CDFI分数维的计算采用数格子法,首先用扫描仪将图像输入计算机,在相应的图像处理软件中用不同大小的格子覆盖图像,分别计算不同大小的格子与血流信号相交的格子总数,以格子边长(mm)倒数的对数为横坐标,以相交格子总数的对数为纵坐标做双对数曲线,图形线性部分的斜率即分数维值。
结 果
1.计算结果显示当格子边长小于1.0mm时图形具有线性特征,格子边长再增大时图形开始弯曲,因此分数维的值采用了该段线性部分的斜率(见图1)。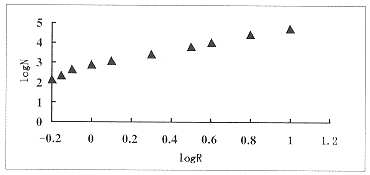
图1 正常肾脏双对数曲线,N-格子总数;R-边长的倒数(mm)
2.用药前、后肾脏CDFI分数维值分别为1.90±0.05和1.51±0.04,两者有显著性差异(P<0.001)。
, http://www.100md.com
3.用药前、后肾脏CDFI的分数维均大于其拓扑维数(Dt=1)。
4.对已知分形维数图形的计算结果显示该方法的误差小于1.3%(见图2)。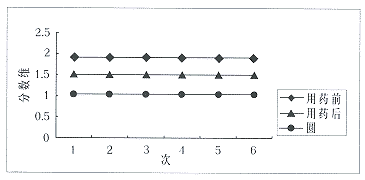
图2 圆和用药前、后肾脏的分数维值
讨 论
超声作为一种无创伤的影像诊断方法已在肾脏疾病的诊断中得到了广泛应用,它不但能够观察肾脏的形态、大小、结构及内部回声,彩色多普勒还能够实时、动态地显示肾内的血流状态(图3)。由于肾脏血流信号没有特定的几何形状,我们很难用传统的几何学方法进行定量。以前的研究多采用定性或半定量的方法,有作者将肾内血流信号的丰富程度分为四型:Ⅰ:充满型;Ⅱ:边缘缺损型;Ⅲ:星点型;Ⅳ:无血流型。由于该方法不能反映血流信号的细微变化,因此如果能够对彩色血流信号的丰富程度进行定量必将有重要的应用价值。1975年美国哈佛大学数学系教授曼德勃罗特(Mandelbrot)〔3〕提出的分形理论则很好的解决了这一问题。分形理论的研究对象是不规则的没有一定形状的物体,并且能够用分数维来进行定量表达,他也因此于1985年荣获了全美科学院推荐的Barnard奖(每五年推荐1名)。该理论认为如果物体的分数维数恒大于其拓扑维数,那么该物体即具有分形特征性并可以用分数维进行定量。本文的计算结果显示肾脏CDFI的分数维均大于其拓扑维数(Dt=1),说明肾脏CDFI具有分形特征。分形物体分为有规分形和无规分形两种,所谓有规分形是指数学上具有严格自相似性的图形,具有无穷层次的自相似结构,如Coch曲线。但自然界中均为无规分形,也就是说该物体只有在一定的标度范围内具有自相似性,在此范围以外就不是分形了。从本研究可以看出肾脏CDFI为无规分形,因为只有当格子边长小于1.0mm时才具有分形特征。分数维很好地表达了分形物体的特征,在二维系统内,分数维数越大表明研究对象在其所处平面内的覆盖程度越大,分形维数为2表明该平面完全被研究对象覆盖,1表明该平面内没有任何研究对象(数学中的理想线段不具有宽度)。用药后肾脏CDFI分数维减小表明了肾内彩色血流信号减少(图4),原因可能是肾脏皮质部小血管壁增厚、管腔狭窄(病理证实),使得血流速度减低、流量减少,彩色多普勒无法显示出来。
, 百拇医药
图3 正常兔子肾脏彩色血流图
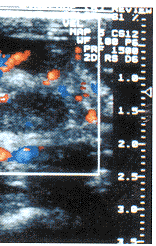
图4 用药21天后的彩色血流图
结论:1.肾脏的CDFI具有分形特征,血流的丰富程度可以用分数维进行定量表达;2.CsA能够引起肾内血流信号减少。
参考文献
1 谢晓燕,吕明德。彩色多普勒能量显像分级法诊断移植肾急性排斥反应。中国超声医学杂志,1997,13(6):45~47
2 Jinzaki M,Ohkuma K,tanimoto A.et al.Small solid renal lesions:Usefulness of power Doppler US.Radiology 1998,209:543~550
3 Mandelbrot BB.The fractal Geometry of Nature.San Francisco:Freeman,1982
(1999-04-07收稿), http://www.100md.com
单位:李振彩(100037 北京解放军第304医院超声科);高云华(重庆市第三军医大学新桥医院超声科)
关键词:分形;分数维;肾脏;彩色多普勒血流图;兔;环孢素A
中国超声医学杂志991003
摘 要 目的:1.判断兔肾脏CDFI是否具有分形特征并探讨该定量方法的实际应用价值;2.研究环孢素A(CsA)对兔肾脏血流的影响。方法:选用体重(1.75kg~1.80kg)相当的雄性新西兰大白兔6只,每天静脉注射CsA 15mg/kg共21天,然后用彩色多普勒观察肾内的血流变化。采用数格子法对用药前、后肾内血流信号进行定量。结果:用药前、后肾脏彩色血流的分数维平均值分别为1.90±0.05和1.51±0.04,均大于其拓扑维数(Dt=1),这说明肾血管树具有分形结构。用药后肾脏CDFI的分数维值明显小于用药前。结论:1.肾脏的CDFI具有分形特征并可用分数维进行定量计算;2.CsA能够引起肾内血流信号的减少。
, http://www.100md.com
A New Quantitative Method of the Renal Color Doppler Flow Signals
Li Zhencai,Gao Yunhua
PLA 304 Hospital,Beijing 100037
ABSTRACT Objective:The aims of this paper are:1.To determine whether the rabbit renal color Doppler flow imaging(CDFI)has a fractal structure and to discuss the practicality of this quantitative methed;2.To assess the effect of Cyclosporine A(CsA)on the intrarenal blood flow of rabbit kidneys.Methods:CsA was administered intravenously for 21 days at doses of 15 mg/kg/d to six male New Zealand White rabbits(weighting 1.75~1.80kg).Then,the intrarenal blood flow was assessed by color Doppler ultrasound.The fractal dimensions of renal CDFI were calculated using an implementation of the box-counting method on an imaging analysis system before and after drug administration.Results:Before and after drug administration,the mean fractal dimensions were 1.90±0.05 and 1.51±0.04 respectively,which were significantly greater than its topological dimension(Dt=1),indicating that the renal CDFI has a fractal structure.After the drug administration the fractal dimensions were significantly less then the before drug administrations.Conclusion:1.The CDFI of the kidney has a fractal structure and can be measured by fractal dimension.2.CsA can reduce the renal color Doppler signals.
, http://www.100md.com
KEY WORDS Fractals Fractal Dimension Kidney Color Doppler fLow imaging Rabbit Cyclosporine A
由于肾脏彩色血流信号不规则也没有特定的几何形状,我们很难用传统的几何学方法进行定量。以前的研究多采用定性或半定量的方法〔1,2〕,但不能反应血流信号的细微变化。为此,本文的主要目的是(1).判断肾脏彩色血流图像(CDFI)是否具有分形特征并探讨该定量方法的实际应用价值;(2)研究环孢素A(CsA)对兔肾脏血流的影响。
资料与方法
选用体重(1.75kg~1.80kg)相当的雄性新西兰大白兔6只,每天静脉注射CsA 15mg/kg,注射前用生理盐水将CsA稀释为1ml,整个实验过程共21天。超声检查时间分别为用药前和用药后第21天,每次超声检查时用3%的戊巴比妥钠30mg/kg麻醉动物(静脉注射),然后用探头反复扫查双侧肾脏,尽量获得经过肾门的最大冠状切面,用彩色多普勒观察肾内的血流状况,调节彩色多普勒增益并尽量消除背景噪声,条件设置如下:彩色增益85%、壁滤波50、彩色血流最低流速3.0cm/s。最后记录彩色多普勒血流图像。仪器:采用ATL HDI型超9(ultramark 9)彩色多普勒超声仪,探头频率5.0~10.0MHz。
, http://www.100md.com
计算方法:肾脏CDFI分数维的计算采用数格子法,首先用扫描仪将图像输入计算机,在相应的图像处理软件中用不同大小的格子覆盖图像,分别计算不同大小的格子与血流信号相交的格子总数,以格子边长(mm)倒数的对数为横坐标,以相交格子总数的对数为纵坐标做双对数曲线,图形线性部分的斜率即分数维值。
结 果
1.计算结果显示当格子边长小于1.0mm时图形具有线性特征,格子边长再增大时图形开始弯曲,因此分数维的值采用了该段线性部分的斜率(见图1)。

图1 正常肾脏双对数曲线,N-格子总数;R-边长的倒数(mm)
2.用药前、后肾脏CDFI分数维值分别为1.90±0.05和1.51±0.04,两者有显著性差异(P<0.001)。
, http://www.100md.com
3.用药前、后肾脏CDFI的分数维均大于其拓扑维数(Dt=1)。
4.对已知分形维数图形的计算结果显示该方法的误差小于1.3%(见图2)。

图2 圆和用药前、后肾脏的分数维值
讨 论
超声作为一种无创伤的影像诊断方法已在肾脏疾病的诊断中得到了广泛应用,它不但能够观察肾脏的形态、大小、结构及内部回声,彩色多普勒还能够实时、动态地显示肾内的血流状态(图3)。由于肾脏血流信号没有特定的几何形状,我们很难用传统的几何学方法进行定量。以前的研究多采用定性或半定量的方法,有作者将肾内血流信号的丰富程度分为四型:Ⅰ:充满型;Ⅱ:边缘缺损型;Ⅲ:星点型;Ⅳ:无血流型。由于该方法不能反映血流信号的细微变化,因此如果能够对彩色血流信号的丰富程度进行定量必将有重要的应用价值。1975年美国哈佛大学数学系教授曼德勃罗特(Mandelbrot)〔3〕提出的分形理论则很好的解决了这一问题。分形理论的研究对象是不规则的没有一定形状的物体,并且能够用分数维来进行定量表达,他也因此于1985年荣获了全美科学院推荐的Barnard奖(每五年推荐1名)。该理论认为如果物体的分数维数恒大于其拓扑维数,那么该物体即具有分形特征性并可以用分数维进行定量。本文的计算结果显示肾脏CDFI的分数维均大于其拓扑维数(Dt=1),说明肾脏CDFI具有分形特征。分形物体分为有规分形和无规分形两种,所谓有规分形是指数学上具有严格自相似性的图形,具有无穷层次的自相似结构,如Coch曲线。但自然界中均为无规分形,也就是说该物体只有在一定的标度范围内具有自相似性,在此范围以外就不是分形了。从本研究可以看出肾脏CDFI为无规分形,因为只有当格子边长小于1.0mm时才具有分形特征。分数维很好地表达了分形物体的特征,在二维系统内,分数维数越大表明研究对象在其所处平面内的覆盖程度越大,分形维数为2表明该平面完全被研究对象覆盖,1表明该平面内没有任何研究对象(数学中的理想线段不具有宽度)。用药后肾脏CDFI分数维减小表明了肾内彩色血流信号减少(图4),原因可能是肾脏皮质部小血管壁增厚、管腔狭窄(病理证实),使得血流速度减低、流量减少,彩色多普勒无法显示出来。


, 百拇医药
图3 正常兔子肾脏彩色血流图


图4 用药21天后的彩色血流图
结论:1.肾脏的CDFI具有分形特征,血流的丰富程度可以用分数维进行定量表达;2.CsA能够引起肾内血流信号减少。
参考文献
1 谢晓燕,吕明德。彩色多普勒能量显像分级法诊断移植肾急性排斥反应。中国超声医学杂志,1997,13(6):45~47
2 Jinzaki M,Ohkuma K,tanimoto A.et al.Small solid renal lesions:Usefulness of power Doppler US.Radiology 1998,209:543~550
3 Mandelbrot BB.The fractal Geometry of Nature.San Francisco:Freeman,1982
(1999-04-07收稿), http://www.100md.com