有约束模拟退火法优化3D立体定向放射治疗计划*
作者:吴新根1 吕维雪2 罗立民1
单位:1 (东南大学 生物医学工程系,南京 210096);2 (浙江大学 生物医学工程研究所,杭州 310027)
关键词:立体定向放射治疗计划;线性规划法;有约束模拟退火法;优化
生物医学工程学杂志980311 内容摘要 采用线性规划法与改进的有约束模拟退火法相结合,优化X-刀立体定向放射治疗计划。第一阶段的线性规划法可以缩小解空间,以利于第二阶段的有约束模拟退火法采用较小的权值修正粒度。实验研究表明:经过两个阶段优化,我们达到了放射治疗计划优化的目的。
Application of Constrained Simulated Annealing to 3D
, http://www.100md.com
Stereotactic Radiothrapy Treatment Planning
Wu Xingen1 Lu Weixue2 Luo Limin1
1 (Southeast University,Nanjing 210096)
2 (Zhejiang University,Hangzhou 310027)
Abstract In this paper,linear programming and constrained simulated annealing are combined to optimize X-knife stereotactic radiothrapy treatment planning.In the first phase,linear programming reduces the resolution space,which is favourable to the adoption of little granularity in the second phase.Our experiment demonstrates that after the two-phase optimization,we attain the expected result.
, 百拇医药
Key words Stereotactic radiothrapy treatment planning Linear programming Constrained simulated annealing Optimization
1 引 言
所谓放射治疗计划是为了达到对靶体施行高剂量照射以产生不可恢复性损毁而同时使周围正常组织所受影响尽量最小的目标,而选择最好的照射方案的过程。这样的方案包括一些自由参数,如射线能量、机架、治疗床转动角度等的选择。早期的放疗计划是一种“手工规划(hand planning)”过程,随着计算机应用于规划过程,剂量分布计算工作由计算机完成,而计划者负责选择自由参数。这是一个反复的试错(trial and error)过程,在找到合适的方案之前要一直进行下去。这种半手工方式的局限是很明显的。更为合理的计划思想应该是:从治疗专家制定的剂量处方出发寻找最佳的参数配置,而上述做法只能找到一个可行方案,没有优化过程。优化理论应用于放射治疗计划始于1967年Hope等人[2]在计划中所用的记分函数(score function),自那时到现在,治疗计划优化理论得到了很大的发展。下面我们对各种优化方法进行简要的介绍与评估。
, http://www.100md.com
2 优化方法综述
在放射治疗中所用的优化方法大致有记分函数评估法(score function programming)、线性规划法(linear programming)、参数优化法(parametric programming)、均方优化法(quadriatic programming)、投影梯度法(gradient projection)、有约束模拟退火法(constrained simulated annealing)等。现逐一对它们进行简述。
2.1 记分函数评估法
记分函数是一种非线性、非分析性函数,通过给每个治疗计划一个数值来评估、比较不同的计划,能使记分函数得到最高分的计划即为最优的计划。过去所用的记分函数基于如下一些标准,如射束方位、靶体内剂量均匀性、相对于最大剂量的肿瘤剂量、积分剂量、敏感器官的剂量、病灶可能转移区的剂量等。其最大特点是评分标准的普遍性。一些取连续值的变量,如相对肿瘤权值,被约束成只能取多个离散值。但是,当变量个数增加或用离散值逼近连续变量的个数增加时,评分函数会由于搜索而使评估时间迅速增加。严格地说,此种方法不是真正的优化方法。
, 百拇医药
2.2 线性规划法
是一种非常适用于放射治疗计划的有约束优化法,是通过求解一组线性约束等式和不等式、约束每个变量非负值及最小化一个线性目标函数实现的。线性规划法的不足是,当不满足约束条件时就不能产生一个近似可行解,更严重的不足是其线性目标函数,临床适用或期望的目标函数可能无法用一个线性目标函数来表示。
2.3 参数优化法
Bahr等人[7]将此法与线性规划法结合起来使用,他们经过调查后认为:靶体内剂量均匀性的取得是以周围区域剂量提高、入射束数目增加为代价的。由于剂量均匀性是通过在预选约束点上设置剂量的上限和下限实现的,因而当这两个限的变化范围太小时,就可能没有解;同样,如果变化范围太大,剂量均匀性效果不会太好。因此,常用几个范围来寻找适当的解。它的主要缺点是定义目标函数时所强加的线性关系。
, http://www.100md.com 2.4 均方优化法
均方优化法的主要特点是待最小化的目标函数是上个二次项,满足的约束条件与线性优化法相同。这个二次目标函数主要是对靶体剂量均匀性的反映。最通用的均方优化方案将均方问题分解为线性规划子问题。然后用单纯形法求其解。显然,与直接用线性优化方法相比需要更多的计算时间。与线性规化法相同,在问题没有解时,不会给出一个可行解,但对特殊类型的均方优化问题,在没有解时也可能用十分快速的算法获得一个近似解。
2.5 投影梯度法
与寻找全局最优解的上述方法不同,投影梯度法是一种递归技术,用于改进一个已有的解。在每一次递归中,基于目标函数对参数变量的导数,对这些变量进行修改。投影梯度最突出的优点是:如果用数值导数(分析导数也可用),那么优化函数可以是任何形式。但是,投影梯度法不能保证一个全局最优解,而计算时间可能很长。Legrus等报道他们用的线性优化法比投影梯度法大致快50倍。
, 百拇医药
2.6 有约束模拟退火
模拟退火法最早是由Metropolis[5]于1953年提出来的,而Kirkpatrick等人[4]最先于80年代初用它解决优化问题。由于模拟退火法综合利用了蒙特卡罗法和爬山法来解决优化问题,避免陷入局部最优,因此在解决组合优化问题方面取得了令人满意的结果。模拟退火法应用于放射治疗计划始于1989年,S.Webb[3]应用模拟退火方法最小化代价函数期望剂量分布与计算剂量分布之间误差的平方。有约束的模拟退火法是在选取配置时,如果参数不满足约束条件,那么就彻底放弃,而不是以概率e-βΔE接受(β与有效温度有关,ΔΕ是新、旧配置条件下目标函数之差)。相对于线性法和均方优化法来说,有约束模拟退火法的主要优点之一是其目标函数的数学形式没有限制,用它可以模拟放射损毁的生物效应等。不足的是,约束模拟退火计算十分缓慢,特别是在放射治疗自由参数较多的情况下,更是如此。
, http://www.100md.com
3 两阶段放射治疗优化法
我们在仔细分析了各种目标函数和优化方法后提出了如下放射优化方法:
线性规划方法比较适合提出一个初步解,但是线性目标函数很难反映靶体内剂量均匀性这一特性,因此有必要将线性规划算法得到的解作为模拟退火优化算法的初始点。靶体、高剂量尽量均匀一致和周围正常组织剂量最小化组成这个阶段的目标函数。第一阶段采用线性优化法的另一个作用是缩小解空间,加快了模拟退火法速度。下面分别详细介绍这二阶段优化方法。
3.1 线性规划放射治疗计划
如前所述,此阶段的主要目的是从众多的射束自由参数中找到合适的解作为下一阶段均方优化的起始点。假设靶体内约束点共有Nt,而周围正常组织内的约束点共有Ns,各种射束的总数为Nb。djk是第k条射束在靶体内第j点产生的单位化后剂量,而Sik为第k条射束在周围正常组织内第i点产生的单位化后剂量,则对于靶体内每一点,有如下的约束条件: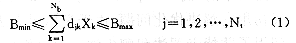
, http://www.100md.com
其中:Xk为第k条射束的非负权值,Bmin、Bmax分别为靶体内各点所能接受的最小、最大剂量。而对于周围正常组织内每一点,则有如下约束: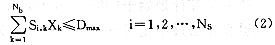
其中:Dmax为周围正常组织内各点剂量的最大值。
设靶体内所有约束点的剂量DT为: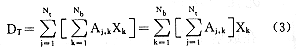
其中:Ajk为第k条射束第j点产生的剂量。正常组织内所有约束点产生的剂量Ds为: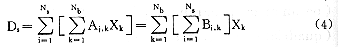
, 百拇医药
其中:Bi,k为第k条射束在第i点产生的剂量。我们可以如下定义线性目标函数。
maxZ=max(DT-Ds)(5)
表示在满足约束条件(式(1)、(2))下,保证靶体内剂量尽量最大而正常组织所受剂量尽量小。
综合上述说明,不等式约束线性规划放射治疗问题可以如下定义:
寻找X=(X1,X2,…,XN)值,使满足
并且使用目标函数
, http://www.100md.com
因此共有(2Nt+Ns)个约束方程。对于(1)、(2)式中“≤”约束,可以引入松弛变量使之成为等式约束,而对于“≥”约束,可以引入剩余变量使之变为等式约束,用常用的单纯形算法求解。
3.2 基于有约束模拟退火法的放射治疗计划
在这个阶段我们将用线性优化放射治疗计划得到的解作为模拟退火法起始点,它的目标函数是一个二次方的函数,定义如下:
这里dj,k为射束k在靶体第j点产生的剂量,xk为第k条射束权值,而Bj为第j点的期望剂量值,Nt,Nb分别为预选靶体内约束点和射束数。这个目标函数的最小化可以使各射束在预选点产生的剂量与期望剂量靠近,如果各点期望剂量相近,就可以实现靶体高剂量区的均匀性。
, 百拇医药
在一些均方目标函数定义中,常将周围正常组织区预选点剂量与最大可接受剂量也放在目标函数中最小化,这些做法的结果将使这些预选点的剂量与最大可接受剂量靠近,我们认为不太合理。实际上,在这些点只要约束一个最大可接受剂量即可,其剂量值在0与这个最大值之间。因此可以对上述射束权值进行如下约束:
此外,对于每个射束权值xk,也进行如下约束:a[k]≤xk≤b[k]、a[k]、b[k]取最小、最大值。
有约束模拟退火法与组合优化问题中使用的模拟退火算法相比,在如下两个方面不同:①对每次随机选取的参数配置必须符合附加的约束条件,否则就被放弃,而不是以概率exp(-Δf/KT)接受随机选取的参数变化。②参数变化空间是一个连续空间,基于粒度(granularity)的权值参数修正是随机选择的。对预选点剂量进行的约束与线性优化放射治疗计划的约束相同,即周围正常组织的剂量必须小于某个可接受的剂量,而对靶体内点的剂量必须大于某个足以给肿瘤组织造成不可逆性损毁所需的剂量,同时小于某一个最大可接受剂量。
, 百拇医药
模拟退火技术十分灵活,不同的目标函数、约束和退火方案易于实现。然而,其计算时间和内存需求也会随着参数个数的增加而线性增加。这个缺点由于我们在第一个阶段的优化,大大减少了参数个数,因而得以克服。其它的不足包括:较其它优化技术速度慢,其优化方案依赖于随机生成的配置序列及所选的退火方案。例如选取不同的随机种子会产生不同的优化方案。但文献[6]中表明,如果“温度”T的下降足够缓慢,系统状态能够趋向于全局最优解。这并不是说能保证得到最优解;得到一个接近于最优解的解则是可能的。
有约束模拟退火算法共分四个部分,它们是互相联系的,构成一个循环过程。这四个部分为:
(1)配置随机选取部分,从第二个阶段得到的解出发,产生一个新的配置。我们称变量修改的尺度为粒度,用G表示。
(2)约束条件测试部分,对生成的新配置首先检测其是否满足约束条件。如果不满足,回到(1)。
, 百拇医药
(3)接受部分,对满足约束的新配置计算目标函数变化值Δf,如果Δf<0,则表明新配置能使目标函数值下降,接受这个新配置。反之,则以一个类似于Boltzmann分布的exp(-Δf/KT)概率随机接受。
(4)确定温度T和粒度G下降部分,以便进行下一个循环。
为了加快优化过程,我们进行了如下的算法改进:对所有变量进行随机变化,而不仅对一个或二个射束权值进行变化。这样做的优点是能够在f函数的“窄谷”中找到最小值。一次只改变一个权值不仅效率低,而且使最小化目标函数只沿着某一个轴前进。对于粒度G,采取先大后小的方法,随着迭代的继续,减少粒度。而对于新配置的产生,则用如下的高斯生成函数:设有几个变量参数,其变化可用X=(x1,x2,…,xn)表示,并从如下高斯概率分布中抽样:
, 百拇医药
式中:G(t)为粒度随迭代次数t变化。因此,对射束权值配置的修改可以表示为:
Xnew=Xold+X(12)
式中:Xnew、Xold为新、旧配置。对于温度T可采用如下降温模式:
T(t)=T0/ln(l+t)(13)
而粒度G的下降模式为:
G(t)=G/(l+t/R)(14)
T0、G0、R由实际经验获取。终止优化过程的标准是满足如下条件:
Δf/f<ε(15)
, 百拇医药
式中:ε为一个很小的正数,一般取10-3或更小。
4 实 验
假设采用10 Mv能量的X-刀直线加速器进行动态旋转治疗,治疗床起始角度为75°,每隔10°旋转一次,终止角度为-75°;机架起始角度为30°,每隔20°旋转一次,终止角度为330°。选取3片CT断层图像,在完成肿瘤分割、等中心确定、周围正常组织指定之后选取剂量约束点。对由3D剂量计算、非均质模型校准得到的剂量见文献[1]进行两阶段优化,最终得到一个放射治疗计划。
在每一片图像中抽取八个点作为剂量约束点,其中六个点落在正常组织结构内。假设等中心坐标在第二片的(62,56,1),经等中心点归一化后得到各点百分剂量。
假设肿瘤内点的处方剂量为50 Gy,最大可允许的变化在±5%之间。三个正常组织最大接受剂量分别为肿瘤剂量的40%、30%和20%,经过两个阶段优化后的剂量为:
, http://www.100md.com
肿瘤区预选点剂量(单位:Gray):
49.915573 49.917576 50.520657
50.622009 48.622749 50.079533
肿瘤区约束剂量范围:(47.5,52.5)。
第一个正常组织预选点剂量(单位:Gray):
1.562023 0.851774 1.291847
0.655342 0.230006 0.177494
第一个正常组织最大可接受剂量为:20Gy。
第二个正常组织预选点剂量(单位:Gray):
, http://www.100md.com
0.176291 3.248497 0.410912
0.312193 0.367838 0.143057
第二个正常组织最大可接受剂量为:15Gy。
第三个正常组织预选点剂量(单位:Gray):
0.299626 0.225205 0.109002
0.392077 0.123236 0.272128
第三个正常组织最大可接受剂量为:10Gy。
假设可以忽略小于0.05Gy的射束权值,则得到的权值(单位:Gray)为:
(65°,50°):0.0519 (25°,130°):0.0537
, 百拇医药
(-25°,230°):33.730 (-45°,270°):0.0644
(-55°,290°):0.0730 (-75°,330°):16.360
图1、图2分别为第一、第二阶段得到的等剂量图,分别为数90%,70%,50%,…。
图1 第一阶段 图2 第二阶段
Fig 1 The first phase Fig 2 The second phase
比较这两个阶段的等剂量图,我们可以认为:第二阶段得到的优化计划比第一阶段的要好。
5 讨 论
, 百拇医药
由以上剂量分布可以看出;经过两个阶段优化,我们达到了放射治疗计划优化的目的,即使靶体受到大的剂量,并且均匀一致,同时使周围正常组织的剂量尽量减小。
从上面的工作,我们认为还有如下几点有待改进:
(1)放射治疗优化面向临床实践,我们期待着在这方面继续深入下去。
(2)本方法也适用于一般的放射治疗,如带有锲形滤板、束平整滤板、由计算机控制叶片活动的准直器、不规则射野等等,进一步的工作将把上述自由参数也考虑进去。
(3)在肿瘤可能转移的区域给定一个较高的剂量,也是优化的一个标准,这方面的工作也有待于和治疗专家进一步的合作。
*中国博士后基金资助项目
参 考 文 献
, 百拇医药
1 吴新根.3D可视化X-刀放射治疗计划系统.浙江大学搏士后研究工作的报告.1996
2 Hope CS,Laurie J,Orr JS et al.The optimization of X-ray treatment planning by computer judgement.Phys.Med.Biol.1967;12∶531
3 Webb S.Optimization of conformal radiotherapy dose distribution by simulated annealing.Phys.Med.Biol.1989;34∶1349
4 Kirkpatrik S,Gelatt CD,Vecchi MP.Optimization by simulated annealing.Science.1983;220∶671
, 百拇医药
5 Metroplis N,Rosenbluth A,Rosenbluth M et al.Equation of state calculations by fast computing machines.J.Chem.Phys.1953;21∶1087
6 Geman S,Geman D.Stochastic relation,Gibbs distributions,and bayesian restoration of images.IEEE trans.Patt.Anan.Mach.Int.PAMI.1984;6∶721
7 Bahr GK,Kereaikes JG,Horwitz H et al.The method of linear programming applied to radiation treatment planning.Radiology.1968;91∶686
(收稿:1997-02-26), 百拇医药(吴新根1 吕维雪2 罗立民1)
单位:1 (东南大学 生物医学工程系,南京 210096);2 (浙江大学 生物医学工程研究所,杭州 310027)
关键词:立体定向放射治疗计划;线性规划法;有约束模拟退火法;优化
生物医学工程学杂志980311 内容摘要 采用线性规划法与改进的有约束模拟退火法相结合,优化X-刀立体定向放射治疗计划。第一阶段的线性规划法可以缩小解空间,以利于第二阶段的有约束模拟退火法采用较小的权值修正粒度。实验研究表明:经过两个阶段优化,我们达到了放射治疗计划优化的目的。
Application of Constrained Simulated Annealing to 3D
, http://www.100md.com
Stereotactic Radiothrapy Treatment Planning
Wu Xingen1 Lu Weixue2 Luo Limin1
1 (Southeast University,Nanjing 210096)
2 (Zhejiang University,Hangzhou 310027)
Abstract In this paper,linear programming and constrained simulated annealing are combined to optimize X-knife stereotactic radiothrapy treatment planning.In the first phase,linear programming reduces the resolution space,which is favourable to the adoption of little granularity in the second phase.Our experiment demonstrates that after the two-phase optimization,we attain the expected result.
, 百拇医药
Key words Stereotactic radiothrapy treatment planning Linear programming Constrained simulated annealing Optimization
1 引 言
所谓放射治疗计划是为了达到对靶体施行高剂量照射以产生不可恢复性损毁而同时使周围正常组织所受影响尽量最小的目标,而选择最好的照射方案的过程。这样的方案包括一些自由参数,如射线能量、机架、治疗床转动角度等的选择。早期的放疗计划是一种“手工规划(hand planning)”过程,随着计算机应用于规划过程,剂量分布计算工作由计算机完成,而计划者负责选择自由参数。这是一个反复的试错(trial and error)过程,在找到合适的方案之前要一直进行下去。这种半手工方式的局限是很明显的。更为合理的计划思想应该是:从治疗专家制定的剂量处方出发寻找最佳的参数配置,而上述做法只能找到一个可行方案,没有优化过程。优化理论应用于放射治疗计划始于1967年Hope等人[2]在计划中所用的记分函数(score function),自那时到现在,治疗计划优化理论得到了很大的发展。下面我们对各种优化方法进行简要的介绍与评估。
, http://www.100md.com
2 优化方法综述
在放射治疗中所用的优化方法大致有记分函数评估法(score function programming)、线性规划法(linear programming)、参数优化法(parametric programming)、均方优化法(quadriatic programming)、投影梯度法(gradient projection)、有约束模拟退火法(constrained simulated annealing)等。现逐一对它们进行简述。
2.1 记分函数评估法
记分函数是一种非线性、非分析性函数,通过给每个治疗计划一个数值来评估、比较不同的计划,能使记分函数得到最高分的计划即为最优的计划。过去所用的记分函数基于如下一些标准,如射束方位、靶体内剂量均匀性、相对于最大剂量的肿瘤剂量、积分剂量、敏感器官的剂量、病灶可能转移区的剂量等。其最大特点是评分标准的普遍性。一些取连续值的变量,如相对肿瘤权值,被约束成只能取多个离散值。但是,当变量个数增加或用离散值逼近连续变量的个数增加时,评分函数会由于搜索而使评估时间迅速增加。严格地说,此种方法不是真正的优化方法。
, 百拇医药
2.2 线性规划法
是一种非常适用于放射治疗计划的有约束优化法,是通过求解一组线性约束等式和不等式、约束每个变量非负值及最小化一个线性目标函数实现的。线性规划法的不足是,当不满足约束条件时就不能产生一个近似可行解,更严重的不足是其线性目标函数,临床适用或期望的目标函数可能无法用一个线性目标函数来表示。
2.3 参数优化法
Bahr等人[7]将此法与线性规划法结合起来使用,他们经过调查后认为:靶体内剂量均匀性的取得是以周围区域剂量提高、入射束数目增加为代价的。由于剂量均匀性是通过在预选约束点上设置剂量的上限和下限实现的,因而当这两个限的变化范围太小时,就可能没有解;同样,如果变化范围太大,剂量均匀性效果不会太好。因此,常用几个范围来寻找适当的解。它的主要缺点是定义目标函数时所强加的线性关系。
, http://www.100md.com 2.4 均方优化法
均方优化法的主要特点是待最小化的目标函数是上个二次项,满足的约束条件与线性优化法相同。这个二次目标函数主要是对靶体剂量均匀性的反映。最通用的均方优化方案将均方问题分解为线性规划子问题。然后用单纯形法求其解。显然,与直接用线性优化方法相比需要更多的计算时间。与线性规化法相同,在问题没有解时,不会给出一个可行解,但对特殊类型的均方优化问题,在没有解时也可能用十分快速的算法获得一个近似解。
2.5 投影梯度法
与寻找全局最优解的上述方法不同,投影梯度法是一种递归技术,用于改进一个已有的解。在每一次递归中,基于目标函数对参数变量的导数,对这些变量进行修改。投影梯度最突出的优点是:如果用数值导数(分析导数也可用),那么优化函数可以是任何形式。但是,投影梯度法不能保证一个全局最优解,而计算时间可能很长。Legrus等报道他们用的线性优化法比投影梯度法大致快50倍。
, 百拇医药
2.6 有约束模拟退火
模拟退火法最早是由Metropolis[5]于1953年提出来的,而Kirkpatrick等人[4]最先于80年代初用它解决优化问题。由于模拟退火法综合利用了蒙特卡罗法和爬山法来解决优化问题,避免陷入局部最优,因此在解决组合优化问题方面取得了令人满意的结果。模拟退火法应用于放射治疗计划始于1989年,S.Webb[3]应用模拟退火方法最小化代价函数期望剂量分布与计算剂量分布之间误差的平方。有约束的模拟退火法是在选取配置时,如果参数不满足约束条件,那么就彻底放弃,而不是以概率e-βΔE接受(β与有效温度有关,ΔΕ是新、旧配置条件下目标函数之差)。相对于线性法和均方优化法来说,有约束模拟退火法的主要优点之一是其目标函数的数学形式没有限制,用它可以模拟放射损毁的生物效应等。不足的是,约束模拟退火计算十分缓慢,特别是在放射治疗自由参数较多的情况下,更是如此。
, http://www.100md.com
3 两阶段放射治疗优化法
我们在仔细分析了各种目标函数和优化方法后提出了如下放射优化方法:
线性规划方法比较适合提出一个初步解,但是线性目标函数很难反映靶体内剂量均匀性这一特性,因此有必要将线性规划算法得到的解作为模拟退火优化算法的初始点。靶体、高剂量尽量均匀一致和周围正常组织剂量最小化组成这个阶段的目标函数。第一阶段采用线性优化法的另一个作用是缩小解空间,加快了模拟退火法速度。下面分别详细介绍这二阶段优化方法。
3.1 线性规划放射治疗计划
如前所述,此阶段的主要目的是从众多的射束自由参数中找到合适的解作为下一阶段均方优化的起始点。假设靶体内约束点共有Nt,而周围正常组织内的约束点共有Ns,各种射束的总数为Nb。djk是第k条射束在靶体内第j点产生的单位化后剂量,而Sik为第k条射束在周围正常组织内第i点产生的单位化后剂量,则对于靶体内每一点,有如下的约束条件:
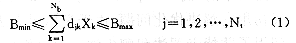
, http://www.100md.com
其中:Xk为第k条射束的非负权值,Bmin、Bmax分别为靶体内各点所能接受的最小、最大剂量。而对于周围正常组织内每一点,则有如下约束:
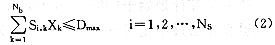
其中:Dmax为周围正常组织内各点剂量的最大值。
设靶体内所有约束点的剂量DT为:
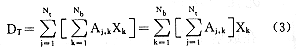
其中:Ajk为第k条射束第j点产生的剂量。正常组织内所有约束点产生的剂量Ds为:
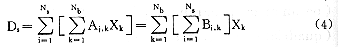
, 百拇医药
其中:Bi,k为第k条射束在第i点产生的剂量。我们可以如下定义线性目标函数。
maxZ=max(DT-Ds)(5)
表示在满足约束条件(式(1)、(2))下,保证靶体内剂量尽量最大而正常组织所受剂量尽量小。
综合上述说明,不等式约束线性规划放射治疗问题可以如下定义:
寻找X=(X1,X2,…,XN)值,使满足

并且使用目标函数

, http://www.100md.com
因此共有(2Nt+Ns)个约束方程。对于(1)、(2)式中“≤”约束,可以引入松弛变量使之成为等式约束,而对于“≥”约束,可以引入剩余变量使之变为等式约束,用常用的单纯形算法求解。
3.2 基于有约束模拟退火法的放射治疗计划
在这个阶段我们将用线性优化放射治疗计划得到的解作为模拟退火法起始点,它的目标函数是一个二次方的函数,定义如下:

这里dj,k为射束k在靶体第j点产生的剂量,xk为第k条射束权值,而Bj为第j点的期望剂量值,Nt,Nb分别为预选靶体内约束点和射束数。这个目标函数的最小化可以使各射束在预选点产生的剂量与期望剂量靠近,如果各点期望剂量相近,就可以实现靶体高剂量区的均匀性。
, 百拇医药
在一些均方目标函数定义中,常将周围正常组织区预选点剂量与最大可接受剂量也放在目标函数中最小化,这些做法的结果将使这些预选点的剂量与最大可接受剂量靠近,我们认为不太合理。实际上,在这些点只要约束一个最大可接受剂量即可,其剂量值在0与这个最大值之间。因此可以对上述射束权值进行如下约束:

此外,对于每个射束权值xk,也进行如下约束:a[k]≤xk≤b[k]、a[k]、b[k]取最小、最大值。
有约束模拟退火法与组合优化问题中使用的模拟退火算法相比,在如下两个方面不同:①对每次随机选取的参数配置必须符合附加的约束条件,否则就被放弃,而不是以概率exp(-Δf/KT)接受随机选取的参数变化。②参数变化空间是一个连续空间,基于粒度(granularity)的权值参数修正是随机选择的。对预选点剂量进行的约束与线性优化放射治疗计划的约束相同,即周围正常组织的剂量必须小于某个可接受的剂量,而对靶体内点的剂量必须大于某个足以给肿瘤组织造成不可逆性损毁所需的剂量,同时小于某一个最大可接受剂量。
, 百拇医药
模拟退火技术十分灵活,不同的目标函数、约束和退火方案易于实现。然而,其计算时间和内存需求也会随着参数个数的增加而线性增加。这个缺点由于我们在第一个阶段的优化,大大减少了参数个数,因而得以克服。其它的不足包括:较其它优化技术速度慢,其优化方案依赖于随机生成的配置序列及所选的退火方案。例如选取不同的随机种子会产生不同的优化方案。但文献[6]中表明,如果“温度”T的下降足够缓慢,系统状态能够趋向于全局最优解。这并不是说能保证得到最优解;得到一个接近于最优解的解则是可能的。
有约束模拟退火算法共分四个部分,它们是互相联系的,构成一个循环过程。这四个部分为:
(1)配置随机选取部分,从第二个阶段得到的解出发,产生一个新的配置。我们称变量修改的尺度为粒度,用G表示。
(2)约束条件测试部分,对生成的新配置首先检测其是否满足约束条件。如果不满足,回到(1)。
, 百拇医药
(3)接受部分,对满足约束的新配置计算目标函数变化值Δf,如果Δf<0,则表明新配置能使目标函数值下降,接受这个新配置。反之,则以一个类似于Boltzmann分布的exp(-Δf/KT)概率随机接受。
(4)确定温度T和粒度G下降部分,以便进行下一个循环。
为了加快优化过程,我们进行了如下的算法改进:对所有变量进行随机变化,而不仅对一个或二个射束权值进行变化。这样做的优点是能够在f函数的“窄谷”中找到最小值。一次只改变一个权值不仅效率低,而且使最小化目标函数只沿着某一个轴前进。对于粒度G,采取先大后小的方法,随着迭代的继续,减少粒度。而对于新配置的产生,则用如下的高斯生成函数:设有几个变量参数,其变化可用X=(x1,x2,…,xn)表示,并从如下高斯概率分布中抽样:

, 百拇医药
式中:G(t)为粒度随迭代次数t变化。因此,对射束权值配置的修改可以表示为:
Xnew=Xold+X(12)
式中:Xnew、Xold为新、旧配置。对于温度T可采用如下降温模式:
T(t)=T0/ln(l+t)(13)
而粒度G的下降模式为:
G(t)=G/(l+t/R)(14)
T0、G0、R由实际经验获取。终止优化过程的标准是满足如下条件:
Δf/f<ε(15)
, 百拇医药
式中:ε为一个很小的正数,一般取10-3或更小。
4 实 验
假设采用10 Mv能量的X-刀直线加速器进行动态旋转治疗,治疗床起始角度为75°,每隔10°旋转一次,终止角度为-75°;机架起始角度为30°,每隔20°旋转一次,终止角度为330°。选取3片CT断层图像,在完成肿瘤分割、等中心确定、周围正常组织指定之后选取剂量约束点。对由3D剂量计算、非均质模型校准得到的剂量见文献[1]进行两阶段优化,最终得到一个放射治疗计划。
在每一片图像中抽取八个点作为剂量约束点,其中六个点落在正常组织结构内。假设等中心坐标在第二片的(62,56,1),经等中心点归一化后得到各点百分剂量。
假设肿瘤内点的处方剂量为50 Gy,最大可允许的变化在±5%之间。三个正常组织最大接受剂量分别为肿瘤剂量的40%、30%和20%,经过两个阶段优化后的剂量为:
, http://www.100md.com
肿瘤区预选点剂量(单位:Gray):
49.915573 49.917576 50.520657
50.622009 48.622749 50.079533
肿瘤区约束剂量范围:(47.5,52.5)。
第一个正常组织预选点剂量(单位:Gray):
1.562023 0.851774 1.291847
0.655342 0.230006 0.177494
第一个正常组织最大可接受剂量为:20Gy。
第二个正常组织预选点剂量(单位:Gray):
, http://www.100md.com
0.176291 3.248497 0.410912
0.312193 0.367838 0.143057
第二个正常组织最大可接受剂量为:15Gy。
第三个正常组织预选点剂量(单位:Gray):
0.299626 0.225205 0.109002
0.392077 0.123236 0.272128
第三个正常组织最大可接受剂量为:10Gy。
假设可以忽略小于0.05Gy的射束权值,则得到的权值(单位:Gray)为:
(65°,50°):0.0519 (25°,130°):0.0537
, 百拇医药
(-25°,230°):33.730 (-45°,270°):0.0644
(-55°,290°):0.0730 (-75°,330°):16.360
图1、图2分别为第一、第二阶段得到的等剂量图,分别为数90%,70%,50%,…。

图1 第一阶段 图2 第二阶段
Fig 1 The first phase Fig 2 The second phase
比较这两个阶段的等剂量图,我们可以认为:第二阶段得到的优化计划比第一阶段的要好。
5 讨 论
, 百拇医药
由以上剂量分布可以看出;经过两个阶段优化,我们达到了放射治疗计划优化的目的,即使靶体受到大的剂量,并且均匀一致,同时使周围正常组织的剂量尽量减小。
从上面的工作,我们认为还有如下几点有待改进:
(1)放射治疗优化面向临床实践,我们期待着在这方面继续深入下去。
(2)本方法也适用于一般的放射治疗,如带有锲形滤板、束平整滤板、由计算机控制叶片活动的准直器、不规则射野等等,进一步的工作将把上述自由参数也考虑进去。
(3)在肿瘤可能转移的区域给定一个较高的剂量,也是优化的一个标准,这方面的工作也有待于和治疗专家进一步的合作。
*中国博士后基金资助项目
参 考 文 献
, 百拇医药
1 吴新根.3D可视化X-刀放射治疗计划系统.浙江大学搏士后研究工作的报告.1996
2 Hope CS,Laurie J,Orr JS et al.The optimization of X-ray treatment planning by computer judgement.Phys.Med.Biol.1967;12∶531
3 Webb S.Optimization of conformal radiotherapy dose distribution by simulated annealing.Phys.Med.Biol.1989;34∶1349
4 Kirkpatrik S,Gelatt CD,Vecchi MP.Optimization by simulated annealing.Science.1983;220∶671
, 百拇医药
5 Metroplis N,Rosenbluth A,Rosenbluth M et al.Equation of state calculations by fast computing machines.J.Chem.Phys.1953;21∶1087
6 Geman S,Geman D.Stochastic relation,Gibbs distributions,and bayesian restoration of images.IEEE trans.Patt.Anan.Mach.Int.PAMI.1984;6∶721
7 Bahr GK,Kereaikes JG,Horwitz H et al.The method of linear programming applied to radiation treatment planning.Radiology.1968;91∶686
(收稿:1997-02-26), 百拇医药(吴新根1 吕维雪2 罗立民1)