Flow Chamber流动实验中非定常流动特性的研究*
作者：樊瑜波 蒋文涛 陈君楷
单位：(四川联合大学 土木工程及应用力学系生物力学所，成都 610065)
关键词：Flow；Chamber；非定常流动；本征函数法
生物医学工程学杂志980309 内容提要 利用本征函数法得到了Flow Chamber流动实验中非定常流动的速度表达式。它不仅满足任意激励形式下的速度变化过程，而且可以描述速度从初始时刻到任意时刻的变化过程。为人们研究非定常流场中的细胞特性提供了理论依据。
A Study of Non-steady Flow Properties in Flow Chamber Experiment
Fan Yubo Jiang Wentao Chen Junkai
, 百拇医药
(Mechanics Department, Biomechanical Institute of Sichuan Union University, Chengdu 610065)
Abstract A time-dependent velocity equation has been achieved by means of eigenfunction method in this paper, which can satisfy any impetus and describe the changing process from the initial time to any time. The theoretical basis is provided to study the nature of blood cells in non-steady flow.
Key words Flow chamber Non-steady flow Eigenfunction method
, http://www.100md.com
1 引 言
Flow Chamber流动实验是目前用于体外定量研究剪切力对血管内皮细胞影响及细胞对血管内皮细胞粘附特性较为常用的方法。其核心部件是一个宽高比较大的矩形截面流动腔(Flow Chamber)。目前，人们已对流动腔内流体作定常流动的情况进行了较多的研究。但是实际上血液在血管中的流动是非定常的，因此，为了更真实地反映剪切力对血管内皮细胞的影响及细胞对血管内皮细胞粘附特性，研究Flow Chamber中非定常流动的特性是必要的。然而，由于问题的复杂性，相关的报道较少。文献[5]虽然对矩形截面管中的脉动流做了一定的分析，但是其仅得到了问题的稳态解，适用范围较小。
*国家自然科学基金资助
本文从流体力学基本方程组出发，结合Flow Chamber中的流动条件，求出了新的流动腔内的速度表达式。为人们研究非定常流场中的细胞特性提供了理论依据。
, http://www.100md.com
图1 Flow Chamber简图
Fig 1 Schematic diagram of Flow Chamber
2 基本方程
假设流体为牛顿流体，流动是充分发展的层流。由问题的对称性，可知流动仅轴向速度u非零，且压力P沿横截面均匀分布。
因此，由连续性方程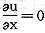
和N-S方程，并结合边界条件，轴向速度分布满足：
其中：ρ、μ分别为流体的密度和粘性系数。
由上式不难看出，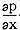
仅与时间t有关。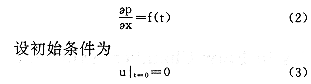
, 百拇医药
由于方程(1)是线性的，因此根据式(1)、(2)、(3)，运用本征函数法，可以得到速度u的级数解形式：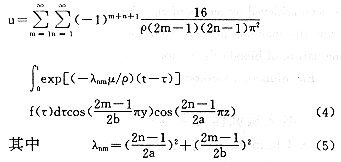
得到了流场速度的分布，则不难得出切应力和剪切率的分布。
3 应用及分析
本文取L＝50mm,a=4.5mm,b=0.13mm,ρ=1.0kg/m3,μ=0.75mPa s,激励f(t)分别取常数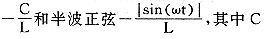
,其中C＝37.24Pa,ω=1.25πs-1。将其代入式(4)得：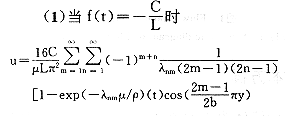
, http://www.100md.com
显然，当t→∞时，u=常数。也就是说当激励为恒定值时，流体的流动将从非定常状态转变为定常状态。这与定常流动的规律是一致的。图2显示了速度从初始状态到定常状态的变化过程，可以看出，t=0.4s时，流动就基本处于定常状态了。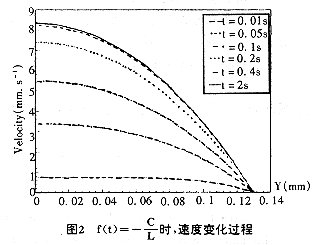
图3表示z=0，y=0～b处的速度场随时间的变化情况。可以看出，速度仅在初始阶段大约四分之一周期内是单调增加的，其后则随着激励发生周期性的变化，并由于流体的粘性作用使得相位略有滞后。
图3 z=0,y=0～b处的速度场随时间的变化过程
Fig 3 The change of velocity with time at z=0 and y=0～b
, 百拇医药
4 结 论
本文利用本征函数法求解Flow Chamber中的非定常流动问题所获得的速度表达式，不仅满足任意激励形式下的速度变化过程，而且可以描述速度从初始时刻开始到任意时刻的变化过程。特别是当激励为恒定值时，还可以回归为定常流动问题的解。
参 考 文 献
1 Frangos JA. Shear Stress Induced Stimulation of Mammakian Cell Metabolism. Biotechnology and Bioengineering. 1988；32∶1053
2 Hammer DA. Dyamics of Cess Adhesion under Hydrodynamic Flow. In Proceedings of the Fourth China Japan-Singapore Conference on Biomechanics. Beijing:International Academic Publishers, 1995∶425
, 百拇医药
3 Davis RT. Numerical Methods for Coordinate Generation Based on a Mapping Technique. In:J.A.Essers Ed. Computational Methods for Turbulent, Transonic, and Viscous Flows, Hemisphere Publishing Corporation, 1983
4 Van-Kooten TG,Schakenraad JM,Van-der-Mei HC et al. Development and use of a parallel-plate flow chamber for studying cellular adhesion to solid surfaces. J.Biomed. Mat.Res, 1992；26∶725
5 乐嘉春，柳兆荣，矩形截面管中脉动流的分析.复旦学报，1993；32(3)∶322
6 王载舆著.数学物理方程及特殊函数.北京：清华大学出版社，1991∶11
(收稿：1997-06-25 修回：1998-01-15), 百拇医药
单位：(四川联合大学 土木工程及应用力学系生物力学所，成都 610065)
关键词：Flow；Chamber；非定常流动；本征函数法
生物医学工程学杂志980309 内容提要 利用本征函数法得到了Flow Chamber流动实验中非定常流动的速度表达式。它不仅满足任意激励形式下的速度变化过程，而且可以描述速度从初始时刻到任意时刻的变化过程。为人们研究非定常流场中的细胞特性提供了理论依据。
A Study of Non-steady Flow Properties in Flow Chamber Experiment
Fan Yubo Jiang Wentao Chen Junkai
, 百拇医药
(Mechanics Department, Biomechanical Institute of Sichuan Union University, Chengdu 610065)
Abstract A time-dependent velocity equation has been achieved by means of eigenfunction method in this paper, which can satisfy any impetus and describe the changing process from the initial time to any time. The theoretical basis is provided to study the nature of blood cells in non-steady flow.
Key words Flow chamber Non-steady flow Eigenfunction method
, http://www.100md.com
1 引 言
Flow Chamber流动实验是目前用于体外定量研究剪切力对血管内皮细胞影响及细胞对血管内皮细胞粘附特性较为常用的方法。其核心部件是一个宽高比较大的矩形截面流动腔(Flow Chamber)。目前，人们已对流动腔内流体作定常流动的情况进行了较多的研究。但是实际上血液在血管中的流动是非定常的，因此，为了更真实地反映剪切力对血管内皮细胞的影响及细胞对血管内皮细胞粘附特性，研究Flow Chamber中非定常流动的特性是必要的。然而，由于问题的复杂性，相关的报道较少。文献[5]虽然对矩形截面管中的脉动流做了一定的分析，但是其仅得到了问题的稳态解，适用范围较小。
*国家自然科学基金资助
本文从流体力学基本方程组出发，结合Flow Chamber中的流动条件，求出了新的流动腔内的速度表达式。为人们研究非定常流场中的细胞特性提供了理论依据。
, http://www.100md.com
图1 Flow Chamber简图
Fig 1 Schematic diagram of Flow Chamber
2 基本方程
假设流体为牛顿流体，流动是充分发展的层流。由问题的对称性，可知流动仅轴向速度u非零，且压力P沿横截面均匀分布。
因此，由连续性方程
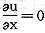和N-S方程，并结合边界条件，轴向速度分布满足：其中：ρ、μ分别为流体的密度和粘性系数。
由上式不难看出，
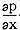仅与时间t有关。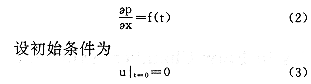, 百拇医药
由于方程(1)是线性的，因此根据式(1)、(2)、(3)，运用本征函数法，可以得到速度u的级数解形式：
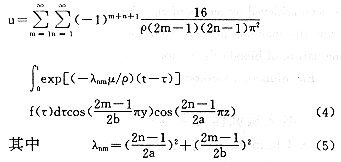
得到了流场速度的分布，则不难得出切应力和剪切率的分布。
3 应用及分析
本文取L＝50mm,a=4.5mm,b=0.13mm,ρ=1.0kg/m3,μ=0.75mPa s,激励f(t)分别取常数
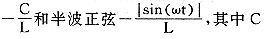,其中C＝37.24Pa,ω=1.25πs-1。将其代入式(4)得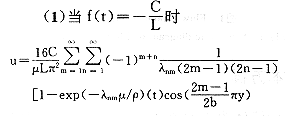：, http://www.100md.com
显然，当t→∞时，u=常数。也就是说当激励为恒定值时，流体的流动将从非定常状态转变为定常状态。这与定常流动的规律是一致的。图2显示了速度从初始状态到定常状态的变化过程，可以看出，t=0.4s时，流动就基本处于定常状态了。
图3表示z=0，y=0～b处的速度场随时间的变化情况。可以看出，速度仅在初始阶段大约四分之一周期内是单调增加的，其后则随着激励发生周期性的变化，并由于流体的粘性作用使得相位略有滞后。
图3 z=0,y=0～b处的速度场随时间的变化过程
Fig 3 The change of velocity with time at z=0 and y=0～b
, 百拇医药
4 结 论
本文利用本征函数法求解Flow Chamber中的非定常流动问题所获得的速度表达式，不仅满足任意激励形式下的速度变化过程，而且可以描述速度从初始时刻开始到任意时刻的变化过程。特别是当激励为恒定值时，还可以回归为定常流动问题的解。
参 考 文 献
1 Frangos JA. Shear Stress Induced Stimulation of Mammakian Cell Metabolism. Biotechnology and Bioengineering. 1988；32∶1053
2 Hammer DA. Dyamics of Cess Adhesion under Hydrodynamic Flow. In Proceedings of the Fourth China Japan-Singapore Conference on Biomechanics. Beijing:International Academic Publishers, 1995∶425
, 百拇医药
3 Davis RT. Numerical Methods for Coordinate Generation Based on a Mapping Technique. In:J.A.Essers Ed. Computational Methods for Turbulent, Transonic, and Viscous Flows, Hemisphere Publishing Corporation, 1983
4 Van-Kooten TG,Schakenraad JM,Van-der-Mei HC et al. Development and use of a parallel-plate flow chamber for studying cellular adhesion to solid surfaces. J.Biomed. Mat.Res, 1992；26∶725
5 乐嘉春，柳兆荣，矩形截面管中脉动流的分析.复旦学报，1993；32(3)∶322
6 王载舆著.数学物理方程及特殊函数.北京：清华大学出版社，1991∶11
(收稿：1997-06-25 修回：1998-01-15), 百拇医药