小波分析用于QT离散度的测量
作者:高 荣 魏义祥 崔长琮
单位:高 荣 魏义祥 (清华大学 工程物理系,北京 100084);崔长琮 (西安医科大学 附一院,西安 710001)
关键词:QT离散度;小波分析;自动测量
生物医学工程学杂志990112 内容摘要 讨论小波分析在QT离散度测量中的运用,提出了用多阈值来定位T波终点的新算法。对计算机测量的结果与手工测量进行了对比,提出采用方差来定义QT离散度的设想。
The Measurement of QT Dispersion Using Wavelet Transformation
Gao Rong1 Wei Yixiang1 Cui Changcong2
, http://www.100md.com
1 (Department of Engineering Physics, Tsinghua University, Beijing 100084)
2 (First Teaching Hospital, Xi'an Medical University, Xi'an 710001)
Abstract This paper addressed the application of wavelet to the measurement of QT dispersion and presented a new method using multi-thresholds to determinate the end point of T-wave. The results geined by computer and human were compared. We also suggested that QT dispersion be defined as the SD of 12 QT intervals.
, 百拇医药
Key words QT dispersion Wavelet transformation Automated measurement
1 概述
QT离散度[1]是指标准十二导联心电图中最大QT间期与最小QT间期之差,是近年来提出并进行讨论的一个用于预测心源性猝死危险性的医学指标。由于手工测量效率低,重复性差,因而缺少大量的统计数据,已成为影响深入讨论的重要因素之一。因此,研究QT离散度的计算机测量方法是一项有意义的工作。
小波分析是一种现代信号处理技术,它能够以多种分辨率来分析信号,具有强抗干扰能力,适合于T波终点检测这类传统信号处理技术难以应付的任务。本文实现了一个基于样条小波的边沿检测算法,并将它用于QT离散度的计算机测量。原始心电图数据及手工测量结果由西安医科大学第一附属医院提供,该院较早与美国Utah大学合作,开展了QT离散度测定方法及临床应用的研究。最后对手工测量与计算机测量的误差进行了分析讨论,表明该算法的测量结果与手工测量的结果比较一致,可以试用于实际的QT离散度自动测量系统中。
, http://www.100md.com
2 小波变换及信号奇异点的检测
用分析小波代替传统的付立叶分析中的正(余)弦基函数,解决了时域局部化与频域局部分化的矛盾。小波变换具有重要的“变焦”特性,可以根据待测信号的需要选择不同的尺度进行“多尺度分析”,在信号奇异点的检测中具有多分辨率分析的能力。
为了便于计算机的处理,将尺度和位移离散化,用s表示尺度因子,t表示平移因子,将小波变换定义为信号与分析小波的卷积而不是内积,可以得到: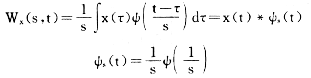
研究小波变换的奇异点与信号变化激烈处的联系,发现检测奇异点的小波类似于一个平滑低通滤波器加一个差分器,这样我们就可以按照传统的检测特征点的思路进行波形定位,确定起点和终点。
为了用小波变换极大值在尺度上的变化来表征信号奇异点的性质,引入李氏指数(Lipschitz exponent)α。对于斜坡函数,α为1;对于阶跃函数,阶跃处α为0;对δ函数,α为-1,可见李氏指数实际上表示了信号在奇异点处的规则性。我们可以量化地表征信号在其突变部位的过渡情况,特别适用于强噪声的背景中检测信号。例如在心电信号的R波检测时,就可以根据李氏指数的大小来区分是真正的R波还是噪声信号。
, 百拇医药
可以证明,当a=2j,t在区间[a,b]时,如果有:
|Wx(j,t)|≤Ksα
or log2|Wx(j,t)|≤log2K+jα
则x(t)在区间[a,b]中为均匀Lipschitz α。其中jα将小波变换的尺度特征j与Lipschitz指数α联系起来,从而反映了小波变换极大值随尺度j的变化规律。
3 小波变换的计算机实现[2,3]
QT间期的测量需要起点和终点的定位,用作边沿检测的小波,应是反对称的。要得到特征点的位置信息,还必须具有线性相位。因此我们选用样条函数的一阶导数作为分析小波,再根据二尺度方程可以得到尺度函数ψ(t)和分析小波ψ(t)如下:
, http://www.100md.com
从小波变换的等效滤波器模型可以看出,小波变换等效为一组带通滤波器。令Qj(ω)表示等效滤波器的传递函数:
可见Q是一有限冲激响应滤波器,它具有线性相位并且是反对称的。
正确选择测量的尺度是抑制噪声、提高测量精度的关键。当尺度小时,带通滤波器中心频率高、带宽大,主要反映的是信号的高频细节;而尺度变大时,带通滤波器的中心频率向低频方向移动,带宽随之变小,主要反映信号的低频细节。根据心电信号的功率谱,QRS包含大量的高频信息,选择在比较小的尺度上测量,突出QRS,且避免了大部分的高频干扰;T波的低频成分多,则在比较大的尺度上进行测量。选定变换用分析小波并且选择了测量尺度之后,对所要测量的心电信号进行小波变换,就得到了比较理想的波形。
4 心电信号特征点的定位及QT间期的测量
, http://www.100md.com
一个单向脉冲的小波变换为一个极大、极小值对,其峰位对应极大、极小值之间的过零点,其起点和终点分别对应极值对的起点和终点。根据这个规律,可以比较容易定位QRS波群的位置以及Q波的起点。而T波终点形态比较复杂,要对高大T波和低平T波分别处理,其中尤以高大T波终点的定位为关键。根据T波与基线的交点情况由极大值PM1峰值的30%、20%、10%和0%四个阈值可以得到四个交点T1、T2、T3和T4。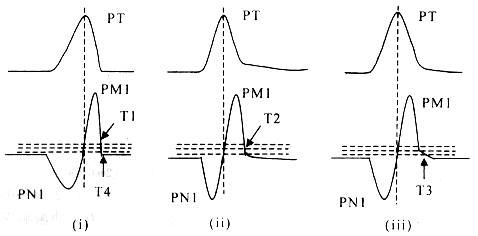
图1 T波的三种形态
Fig 1 Three forms of T wave
第一类,下降支陡峭,与基线的交点明显,受干扰小,满足(T4-T2)<5*(T2-T1)。定位终点时取比较小的阈值,令TE=(T3+T4)/2。
第二类,下降支平缓,末端有一个明显的转折,与基线交点很模糊。满足(T4-T2)>10*(T2-T1)。我们将T2后面的尾巴看作是干扰所致,用T1和T2的外推定义T波的终点:TE=T2+2*(T2-T1)。
, 百拇医药
第三类,介于上述两类T波之间,满足10*(T2-T1)>(T4-T2)>5*(T2-T1)。T波下降支的尾部既不能完全看成是噪声,也不能完全看成是信号。所以我们将T波的终点定在T3和T2之间,即TE=(T2+T3)/2。
上述算法与其它算法的区别在于采用了多阈值结合线性外推,这样充分考虑了T波下降支的各种形态,比较符合人工测量的特点。
用上述方法确定了QRS起点QS和T波终点TE后,QT间期QT=TE-QS。分别对同步十二导联心电图上的十二个导联数据进行上述处理,得到十二个QT。将最大的QT与最小的QT相减,即测得QT离散度QTd。
5 结果与讨论
我们用17个同步十二导联心电图进行了计算机自动测量实验,其结果与手工测量结果对比如下:
, http://www.100md.com
表1 QTd的自动测量结果与手工测量结果
Table 1 QTd value of manual and automatic measurement No
1
2
3
4
5
6
7
8
9
, 百拇医药 QTd
Automatic
68
56
44
61
37
43
49
65
40
Manual
55
, http://www.100md.com
50
35
50
45
40
45
50
40
No
10
11
12
13
14
, 百拇医药
15
16
17
QTd
Automatic
57
38
50
58
48
43
64
67
, 百拇医药
Manual
45
45
50
45
40
60
55
50
QT间期的计算机自动测量与手工测量对比:
平均误差: 3.8 ms
均方根误差: 7.3 ms
17例心电图QT离散度的平均值:
, 百拇医药
手工: 47±6 ms
计算机: 52±10 ms
QT离散度的计算机测量与手工测量误差:
平均误差: 5.2 ms
均方根误差: 9.2 ms
将计算机测量得到的QT间期与手工测量的结果进行直线拟合(ms),结果如下:
y=a+bx
a=31.07±7,5
b=0.92±0.02
r=0.95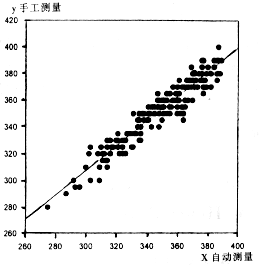
, 百拇医药
图2 QT间期手工与自动测量拟合结果
Fig 2 QT interval fit curve of manual and automatic measurement
结果的分析与讨论:
(1)由测量结果分析可见,QT间期的计算机自动测量与手工测量结果基本吻合,是一个较好的结果,可肯定该算法的意义。计算机测量得到的QTd比由手工得到的略大,似与手工测量习惯有关。差异只有5 ms左右,不影响测量结果的诊断价值,应进一步进行大量临床对比实验。
(2)关于QT离散度的定义:一些文献考虑心率影响,提出心率校正QT离散度,QTc=QTcmax-QTcmin,其中:QTcmax=QTmax/(RR)1/2,QTcmin=QTmin/(RR)1/2;也有文献考虑可能有些导联因无法测量而被抛弃造成QT离散度的计算误差,提出了导联数校正QT离散度,QTa=QTd/(测量导联数)1/2。这些校正算法均有值得离榷之处,我们仍采用未经校正的结果。同时我们也认为一般的QT离散度定义没有充分反映十二个导联的全部信息,容易受错误的测量结果的干扰。我们试用十二个导联QT间期的方差作为QT离散度的定义QTs以图避免以上不足。下面是采用这种定义后的结果:
, 百拇医药
表2 QTs的自动测量结果与手工测量结果
Table 2 QTs value of manual and automatic measurement No
1
2
3
4
5
6
7
8
9
QTs
, http://www.100md.com
Automatic
21
15
11
15
12
13
15
20
14
Manual
19
12
, 百拇医药
12
15
13
14
14
18
13
No
10
11
12
13
14
15
, 百拇医药
16
17
QTs
Automatic
16
16
16
19
13
15
18
22
Manual
, http://www.100md.com
14
15
14
17
10
12
17
17
17个心电图的QTs的平均值:
手工: 14.4±2.5 ms
计算机: 15.9±3.1 ms
QTs的计算机测量与手工测量对比:
, 百拇医药
平均误差: 1.5 ms
均方根误差: 1.6 ms
表明新定义之后的手工测量与计算机测量结果更趋一致,可能比目前QTd的定义更具有特异性。当然,计算方差在临床应用的手工测量中有些困难,故可行性仅供讨论,但计算机自动测量可为之实现创造条件。
(3)T波终点的定义在医学界尚未定论,我们采用的只是其中的一种,在具体的细节上,如各个阈值的取法肯定会存在不少争议。本文旨在推动计算机自动测量算法的实现,以促进QT离散度的研究。参考文献
[1] 陈义汉,龚兰生.QT离散度.中华心血管病杂志,1995;23(4)∶307
[2] Li Cuiwei, Zheng Chongxun, Tai Changfeng. Detection of ECG characteristic points using wavelet transforms. IEEE Trans Biomed Eng, 1995; 42(1)∶21
[3] Mallat S, Hwang WL. Singularity detection and processing with wavelets. IEEE Trans Inform Theory, 1992; 38
(收稿:1997-11-17), 百拇医药
单位:高 荣 魏义祥 (清华大学 工程物理系,北京 100084);崔长琮 (西安医科大学 附一院,西安 710001)
关键词:QT离散度;小波分析;自动测量
生物医学工程学杂志990112 内容摘要 讨论小波分析在QT离散度测量中的运用,提出了用多阈值来定位T波终点的新算法。对计算机测量的结果与手工测量进行了对比,提出采用方差来定义QT离散度的设想。
The Measurement of QT Dispersion Using Wavelet Transformation
Gao Rong1 Wei Yixiang1 Cui Changcong2
, http://www.100md.com
1 (Department of Engineering Physics, Tsinghua University, Beijing 100084)
2 (First Teaching Hospital, Xi'an Medical University, Xi'an 710001)
Abstract This paper addressed the application of wavelet to the measurement of QT dispersion and presented a new method using multi-thresholds to determinate the end point of T-wave. The results geined by computer and human were compared. We also suggested that QT dispersion be defined as the SD of 12 QT intervals.
, 百拇医药
Key words QT dispersion Wavelet transformation Automated measurement
1 概述
QT离散度[1]是指标准十二导联心电图中最大QT间期与最小QT间期之差,是近年来提出并进行讨论的一个用于预测心源性猝死危险性的医学指标。由于手工测量效率低,重复性差,因而缺少大量的统计数据,已成为影响深入讨论的重要因素之一。因此,研究QT离散度的计算机测量方法是一项有意义的工作。
小波分析是一种现代信号处理技术,它能够以多种分辨率来分析信号,具有强抗干扰能力,适合于T波终点检测这类传统信号处理技术难以应付的任务。本文实现了一个基于样条小波的边沿检测算法,并将它用于QT离散度的计算机测量。原始心电图数据及手工测量结果由西安医科大学第一附属医院提供,该院较早与美国Utah大学合作,开展了QT离散度测定方法及临床应用的研究。最后对手工测量与计算机测量的误差进行了分析讨论,表明该算法的测量结果与手工测量的结果比较一致,可以试用于实际的QT离散度自动测量系统中。
, http://www.100md.com
2 小波变换及信号奇异点的检测
用分析小波代替传统的付立叶分析中的正(余)弦基函数,解决了时域局部化与频域局部分化的矛盾。小波变换具有重要的“变焦”特性,可以根据待测信号的需要选择不同的尺度进行“多尺度分析”,在信号奇异点的检测中具有多分辨率分析的能力。
为了便于计算机的处理,将尺度和位移离散化,用s表示尺度因子,t表示平移因子,将小波变换定义为信号与分析小波的卷积而不是内积,可以得到:
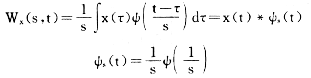
研究小波变换的奇异点与信号变化激烈处的联系,发现检测奇异点的小波类似于一个平滑低通滤波器加一个差分器,这样我们就可以按照传统的检测特征点的思路进行波形定位,确定起点和终点。
为了用小波变换极大值在尺度上的变化来表征信号奇异点的性质,引入李氏指数(Lipschitz exponent)α。对于斜坡函数,α为1;对于阶跃函数,阶跃处α为0;对δ函数,α为-1,可见李氏指数实际上表示了信号在奇异点处的规则性。我们可以量化地表征信号在其突变部位的过渡情况,特别适用于强噪声的背景中检测信号。例如在心电信号的R波检测时,就可以根据李氏指数的大小来区分是真正的R波还是噪声信号。
, 百拇医药
可以证明,当a=2j,t在区间[a,b]时,如果有:
|Wx(j,t)|≤Ksα
or log2|Wx(j,t)|≤log2K+jα
则x(t)在区间[a,b]中为均匀Lipschitz α。其中jα将小波变换的尺度特征j与Lipschitz指数α联系起来,从而反映了小波变换极大值随尺度j的变化规律。
3 小波变换的计算机实现[2,3]
QT间期的测量需要起点和终点的定位,用作边沿检测的小波,应是反对称的。要得到特征点的位置信息,还必须具有线性相位。因此我们选用样条函数的一阶导数作为分析小波,再根据二尺度方程可以得到尺度函数ψ(t)和分析小波ψ(t)如下:

, http://www.100md.com
从小波变换的等效滤波器模型可以看出,小波变换等效为一组带通滤波器。令Qj(ω)表示等效滤波器的传递函数:

可见Q是一有限冲激响应滤波器,它具有线性相位并且是反对称的。
正确选择测量的尺度是抑制噪声、提高测量精度的关键。当尺度小时,带通滤波器中心频率高、带宽大,主要反映的是信号的高频细节;而尺度变大时,带通滤波器的中心频率向低频方向移动,带宽随之变小,主要反映信号的低频细节。根据心电信号的功率谱,QRS包含大量的高频信息,选择在比较小的尺度上测量,突出QRS,且避免了大部分的高频干扰;T波的低频成分多,则在比较大的尺度上进行测量。选定变换用分析小波并且选择了测量尺度之后,对所要测量的心电信号进行小波变换,就得到了比较理想的波形。
4 心电信号特征点的定位及QT间期的测量
, http://www.100md.com
一个单向脉冲的小波变换为一个极大、极小值对,其峰位对应极大、极小值之间的过零点,其起点和终点分别对应极值对的起点和终点。根据这个规律,可以比较容易定位QRS波群的位置以及Q波的起点。而T波终点形态比较复杂,要对高大T波和低平T波分别处理,其中尤以高大T波终点的定位为关键。根据T波与基线的交点情况由极大值PM1峰值的30%、20%、10%和0%四个阈值可以得到四个交点T1、T2、T3和T4。

图1 T波的三种形态
Fig 1 Three forms of T wave
第一类,下降支陡峭,与基线的交点明显,受干扰小,满足(T4-T2)<5*(T2-T1)。定位终点时取比较小的阈值,令TE=(T3+T4)/2。
第二类,下降支平缓,末端有一个明显的转折,与基线交点很模糊。满足(T4-T2)>10*(T2-T1)。我们将T2后面的尾巴看作是干扰所致,用T1和T2的外推定义T波的终点:TE=T2+2*(T2-T1)。
, 百拇医药
第三类,介于上述两类T波之间,满足10*(T2-T1)>(T4-T2)>5*(T2-T1)。T波下降支的尾部既不能完全看成是噪声,也不能完全看成是信号。所以我们将T波的终点定在T3和T2之间,即TE=(T2+T3)/2。
上述算法与其它算法的区别在于采用了多阈值结合线性外推,这样充分考虑了T波下降支的各种形态,比较符合人工测量的特点。
用上述方法确定了QRS起点QS和T波终点TE后,QT间期QT=TE-QS。分别对同步十二导联心电图上的十二个导联数据进行上述处理,得到十二个QT。将最大的QT与最小的QT相减,即测得QT离散度QTd。
5 结果与讨论
我们用17个同步十二导联心电图进行了计算机自动测量实验,其结果与手工测量结果对比如下:
, http://www.100md.com
表1 QTd的自动测量结果与手工测量结果
Table 1 QTd value of manual and automatic measurement No
1
2
3
4
5
6
7
8
9
, 百拇医药 QTd
Automatic
68
56
44
61
37
43
49
65
40
Manual
55
, http://www.100md.com
50
35
50
45
40
45
50
40
No
10
11
12
13
14
, 百拇医药
15
16
17
QTd
Automatic
57
38
50
58
48
43
64
67
, 百拇医药
Manual
45
45
50
45
40
60
55
50
QT间期的计算机自动测量与手工测量对比:
平均误差: 3.8 ms
均方根误差: 7.3 ms
17例心电图QT离散度的平均值:
, 百拇医药
手工: 47±6 ms
计算机: 52±10 ms
QT离散度的计算机测量与手工测量误差:
平均误差: 5.2 ms
均方根误差: 9.2 ms
将计算机测量得到的QT间期与手工测量的结果进行直线拟合(ms),结果如下:
y=a+bx
a=31.07±7,5
b=0.92±0.02
r=0.95

, 百拇医药
图2 QT间期手工与自动测量拟合结果
Fig 2 QT interval fit curve of manual and automatic measurement
结果的分析与讨论:
(1)由测量结果分析可见,QT间期的计算机自动测量与手工测量结果基本吻合,是一个较好的结果,可肯定该算法的意义。计算机测量得到的QTd比由手工得到的略大,似与手工测量习惯有关。差异只有5 ms左右,不影响测量结果的诊断价值,应进一步进行大量临床对比实验。
(2)关于QT离散度的定义:一些文献考虑心率影响,提出心率校正QT离散度,QTc=QTcmax-QTcmin,其中:QTcmax=QTmax/(RR)1/2,QTcmin=QTmin/(RR)1/2;也有文献考虑可能有些导联因无法测量而被抛弃造成QT离散度的计算误差,提出了导联数校正QT离散度,QTa=QTd/(测量导联数)1/2。这些校正算法均有值得离榷之处,我们仍采用未经校正的结果。同时我们也认为一般的QT离散度定义没有充分反映十二个导联的全部信息,容易受错误的测量结果的干扰。我们试用十二个导联QT间期的方差作为QT离散度的定义QTs以图避免以上不足。下面是采用这种定义后的结果:
, 百拇医药
表2 QTs的自动测量结果与手工测量结果
Table 2 QTs value of manual and automatic measurement No
1
2
3
4
5
6
7
8
9
QTs
, http://www.100md.com
Automatic
21
15
11
15
12
13
15
20
14
Manual
19
12
, 百拇医药
12
15
13
14
14
18
13
No
10
11
12
13
14
15
, 百拇医药
16
17
QTs
Automatic
16
16
16
19
13
15
18
22
Manual
, http://www.100md.com
14
15
14
17
10
12
17
17
17个心电图的QTs的平均值:
手工: 14.4±2.5 ms
计算机: 15.9±3.1 ms
QTs的计算机测量与手工测量对比:
, 百拇医药
平均误差: 1.5 ms
均方根误差: 1.6 ms
表明新定义之后的手工测量与计算机测量结果更趋一致,可能比目前QTd的定义更具有特异性。当然,计算方差在临床应用的手工测量中有些困难,故可行性仅供讨论,但计算机自动测量可为之实现创造条件。
(3)T波终点的定义在医学界尚未定论,我们采用的只是其中的一种,在具体的细节上,如各个阈值的取法肯定会存在不少争议。本文旨在推动计算机自动测量算法的实现,以促进QT离散度的研究。参考文献
[1] 陈义汉,龚兰生.QT离散度.中华心血管病杂志,1995;23(4)∶307
[2] Li Cuiwei, Zheng Chongxun, Tai Changfeng. Detection of ECG characteristic points using wavelet transforms. IEEE Trans Biomed Eng, 1995; 42(1)∶21
[3] Mallat S, Hwang WL. Singularity detection and processing with wavelets. IEEE Trans Inform Theory, 1992; 38
(收稿:1997-11-17), 百拇医药