医学数学模型中可积的非线性常微分方程的构造
作者:许虹
单位:许虹(武汉市职工医学院 武汉430016)
关键词:可积;非线性常微分方程;构造;双变换
数理医药学杂志000401
摘 要 为适应医学数学模型构造可积的非线性常微分方程,在应用双变换构造方程的同时,详尽地论述了它的求解步骤,并隐含了可积的非线性常微分方程的求解方法。
中图分类号: O 175.14 文献标识码: A
文章编号:1004-4337(2000)04-0289-03
定理1 若给条件组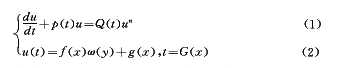
, 百拇医药
其中,p、Q∈C,f、g、ω∈c,n为正整数,且n≠0、1,则可构造出可积的Bernoulli(伯努利)型微分方程:
f(x)ω(y)y+[P(G(x))G(x)f(x)+f(x)]ω(y)
=Q(G(x))G(x)[f(x)ω(y)+g(x)]n-P(G(x)G(x)g(x)-g(x) (3)
且它的通积分为: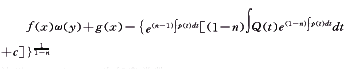 (4)
(4)
这里 t=G(x),c为任意常数。
证明 我们只需将双变换(2)代入可积的Bernoulli方程(1)中,经整理,即可构造出可积的Bernoulli型微分方程(3)。
, http://www.100md.com
反过来,先将Bernoulli型方程(3)变形为: (5)
(5)
再作双变换:
u(t)=f(x)ω(y)+g(x), t=G(x) (6)
此时(5)变形为: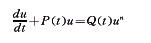
这已是可积的Bernoulli方法,因它的通解为: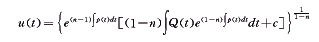 (7)
(7)
再由双变换(6)与(7),即得(3)的通积分为(4)。
, http://www.100md.com
注:很明显,定理1的后一部分是文献[1]中Bernoulli方程的推广。
定理2 若给定条件组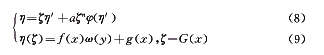
其中,ω、f、g、φ、G∈c,且ω(y)≠const,G(x)≠0,a≠0,n≠1,则可构造出可积的Clairaut(克莱罗)型微分方程: (10)
(10)
且其参数式通积分为: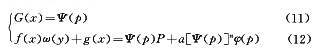
这里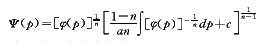
, http://www.100md.com
这里p为参数,c为任意常数。
证明 由文献[2]的推论点2.3,可知(8)为可积的Clairaut型微分方程,因此将双变换(9)代入(8),经整理,即可构造出可积的Clairaut型微分方程(10)。
反过来,先将Clairaut型方程(10)变形为: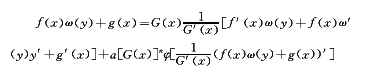 (13)
(13)
作双变换:
η(ζ)=f(x)ω(y)+g(x),ζ=G(x) (14)
此时(13)变形为:
η=ζη+aζnφ(η') (15)
, http://www.100md.com
这已是文献[2]中推论2.3研究的可积的Clairaut型方程,知它的参数式通解为:
其中,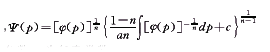
这里p为参数,c为任意常数。
再利用双变换(14),即得(10)的参数式通积分为(11),(12)。
注:定理2中的后一部分,当G(x)=x,f(x)≡1,ω(y)视为f(x)时,即是文献[2]定理2.2所研究的情形。
定理3 若给定条件组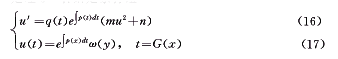
, http://www.100md.com
其中p、q∈c,ω、G∈c,q≠0,m、n为非零常数,则可构造出可积的Riccati(黎卡提)型微分方程:
ω’(y)y+p(x)ω(y)=q(G(x)G(x)e∫pG(x)dG(x)-∫p(x)dx{me2∫p(x)dt[ω(y)]2+n} (18)
且其通积分为:
① 当mn>0时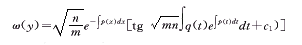 (19)
(19)
② 当mn<0时 (20)
(20)
其中,c1、c2为任意常数
, 百拇医药
证明 由文献[3]定理4的证明中知(16)是可积的特殊的Riccati方程,因而将(17)代入(16)整理后,即可构造出可积的Riccati型方法(18)。
反过来,先将Riccati型方程(18)变形为: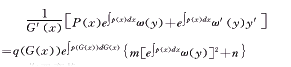 (21)
(21)
作双变换:
u(t)=e∫p(t)dtω(y), t=G(x) (22)
方程(21)变形为: (23)
(23)
由文献[3]定理四的证明中知(23)的通积分为:
, 百拇医药
① 当mn>0时,有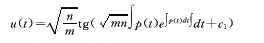
② 当mn<0时,有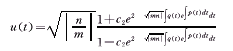
再利用双变换(22),即可得到方程(18)的通积分为(19)与(20)。
注:定理3的后一部分,当G(x)=φ,视ω(y)为y时,即是文献[3]中定理4研究的情形。
定理4 若给定条件组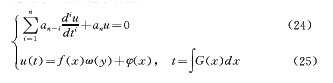
其中,G∈cn-1,f、ω、φ∈cn,G≠0,f≠0,ω≠const,ai=const,i=1,2,3……,n,且约定a0=1,则可构造出可积的n阶微分方程: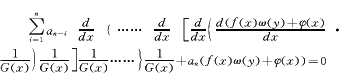 (26)
(26)
, 百拇医药
它可经双变换(25),化为可积的常系数线性微分方程(24)。
证明 将(25)代入可积的高阶常系数线性微分方程(24),即可构造出可积的高阶变系数非线性微分方程(26)。
反过来,应用双变换:
u(t)=f(x)ω(y)+φ(x), t=∫G(x)dx (27)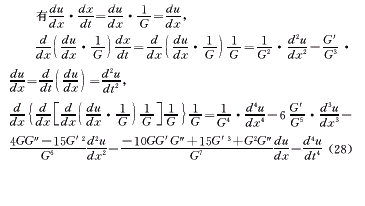 (28)
(28)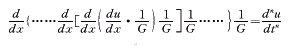
将(28)代入(26)可得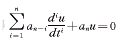 (29)
(29)
(29)已是可积的n阶常数系数线性微分方程。再由双变换(27),可知n阶变系数非线性微分方程(26)可积。
, 百拇医药
当定理4中的n=4时,并由(28)可得
推论 若给定条件组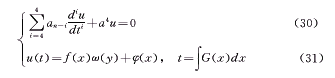
其中,G∈c3,f、ω、φ∈c4,f=f(x)≠0,φ=φ(x)≠0,G=G(x),ω(y)≠const,au=const,i=1,2,3,4,则可构造出可积的四阶变系数非线性微分方程: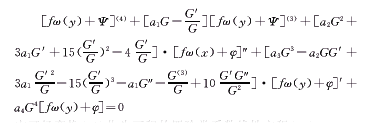 (32)
(32)
它可经变换(31)化为可积的四阶常系数线性方程(30)。
注:本推论的后一部分,即为文献[4]中定理3.2所研究的情形。
定理5 若给定条件组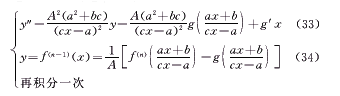
, 百拇医药
再积分一次
其中,f∈cn+1,g∈c,a、b、c、A均为常数,且A≠0,c≠0,a2+bc≠0,n为正整数,n≥1,还约定f(0)=f,则可构造出可积的常微分方程: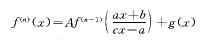 (35)
(35)
证明 易知(33)是可积的二阶非齐次Euler(欧拉)方程,将(34)代入(33),再积分一次,可构造出可积的常微分方程(35)。
事实上,将双变换(34)代入(33),可得:
两边再积分一次得: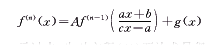
, 百拇医药
反过来,先对方程(35)两边求导得: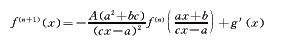 (36)
(36)
再由(35)得变换: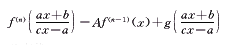 (37)
(37)
及变换:
f(n-1)(x)=y (38)
将双变换(37)与(38)代入(36),整理后得: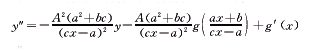
或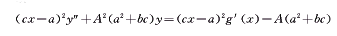
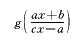
, http://www.100md.com
显然这已是可积的二阶非齐次Euler方程,将它的解代入变换(38)再积分n-1次,可知原方程(35)可积。
注:定理5的后一部分,即为文献[5]的定理1。
参 考 文 献
1,王高雄等编.常微分方程.第二版.北京:高等教育出版社,1983,36.
2,汤光宋.几类微分方程推广与求解.江汉大学学报,1990,7(1):47~53.
3,汤光宋.若干新的一阶变系数常微分方程的可积类型.江汉大学学报(自然科学版).1987,(1):18~26.
4,李恒祥.几类可积的非线性常微分方程(Ⅱ)—高阶方程.应用数学和力学.1990,11(6):521~527.
5,汤光宋.可积常微分方程的新类型.山东轻工业学院学报(自然科学版),1993,(1):71~73.
收稿日期:2000-03-21, http://www.100md.com
单位:许虹(武汉市职工医学院 武汉430016)
关键词:可积;非线性常微分方程;构造;双变换
数理医药学杂志000401
摘 要 为适应医学数学模型构造可积的非线性常微分方程,在应用双变换构造方程的同时,详尽地论述了它的求解步骤,并隐含了可积的非线性常微分方程的求解方法。
中图分类号: O 175.14 文献标识码: A
文章编号:1004-4337(2000)04-0289-03
定理1 若给条件组
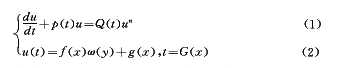
, 百拇医药
其中,p、Q∈C,f、g、ω∈c,n为正整数,且n≠0、1,则可构造出可积的Bernoulli(伯努利)型微分方程:
f(x)ω(y)y+[P(G(x))G(x)f(x)+f(x)]ω(y)
=Q(G(x))G(x)[f(x)ω(y)+g(x)]n-P(G(x)G(x)g(x)-g(x) (3)
且它的通积分为:
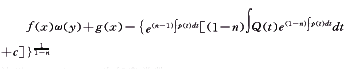 (4)
(4)这里 t=G(x),c为任意常数。
证明 我们只需将双变换(2)代入可积的Bernoulli方程(1)中,经整理,即可构造出可积的Bernoulli型微分方程(3)。
, http://www.100md.com
反过来,先将Bernoulli型方程(3)变形为:
 (5)
(5)再作双变换:
u(t)=f(x)ω(y)+g(x), t=G(x) (6)
此时(5)变形为:
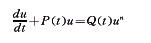
这已是可积的Bernoulli方法,因它的通解为:
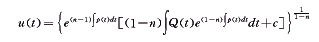 (7)
(7)再由双变换(6)与(7),即得(3)的通积分为(4)。
, http://www.100md.com
注:很明显,定理1的后一部分是文献[1]中Bernoulli方程的推广。
定理2 若给定条件组
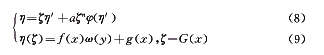
其中,ω、f、g、φ、G∈c,且ω(y)≠const,G(x)≠0,a≠0,n≠1,则可构造出可积的Clairaut(克莱罗)型微分方程:
 (10)
(10)且其参数式通积分为:
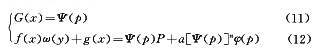
这里
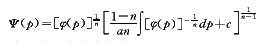
, http://www.100md.com
这里p为参数,c为任意常数。
证明 由文献[2]的推论点2.3,可知(8)为可积的Clairaut型微分方程,因此将双变换(9)代入(8),经整理,即可构造出可积的Clairaut型微分方程(10)。
反过来,先将Clairaut型方程(10)变形为:
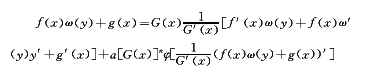 (13)
(13)作双变换:
η(ζ)=f(x)ω(y)+g(x),ζ=G(x) (14)
此时(13)变形为:
η=ζη+aζnφ(η') (15)
, http://www.100md.com
这已是文献[2]中推论2.3研究的可积的Clairaut型方程,知它的参数式通解为:

其中,
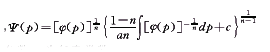
这里p为参数,c为任意常数。
再利用双变换(14),即得(10)的参数式通积分为(11),(12)。
注:定理2中的后一部分,当G(x)=x,f(x)≡1,ω(y)视为f(x)时,即是文献[2]定理2.2所研究的情形。
定理3 若给定条件组
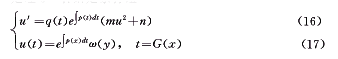
, http://www.100md.com
其中p、q∈c,ω、G∈c,q≠0,m、n为非零常数,则可构造出可积的Riccati(黎卡提)型微分方程:
ω’(y)y+p(x)ω(y)=q(G(x)G(x)e∫pG(x)dG(x)-∫p(x)dx{me2∫p(x)dt[ω(y)]2+n} (18)
且其通积分为:
① 当mn>0时
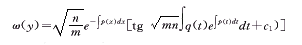 (19)
(19)② 当mn<0时
 (20)
(20)其中,c1、c2为任意常数
, 百拇医药
证明 由文献[3]定理4的证明中知(16)是可积的特殊的Riccati方程,因而将(17)代入(16)整理后,即可构造出可积的Riccati型方法(18)。
反过来,先将Riccati型方程(18)变形为:
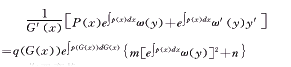 (21)
(21)作双变换:
u(t)=e∫p(t)dtω(y), t=G(x) (22)
方程(21)变形为:
 (23)
(23)由文献[3]定理四的证明中知(23)的通积分为:
, 百拇医药
① 当mn>0时,有
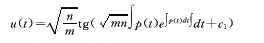
② 当mn<0时,有
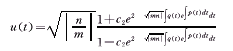
再利用双变换(22),即可得到方程(18)的通积分为(19)与(20)。
注:定理3的后一部分,当G(x)=φ,视ω(y)为y时,即是文献[3]中定理4研究的情形。
定理4 若给定条件组
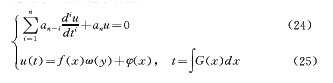
其中,G∈cn-1,f、ω、φ∈cn,G≠0,f≠0,ω≠const,ai=const,i=1,2,3……,n,且约定a0=1,则可构造出可积的n阶微分方程:
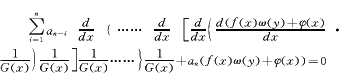 (26)
(26), 百拇医药
它可经双变换(25),化为可积的常系数线性微分方程(24)。
证明 将(25)代入可积的高阶常系数线性微分方程(24),即可构造出可积的高阶变系数非线性微分方程(26)。
反过来,应用双变换:
u(t)=f(x)ω(y)+φ(x), t=∫G(x)dx (27)
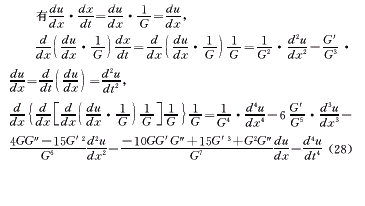 (28)
(28)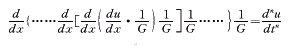
将(28)代入(26)可得
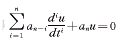 (29)
(29)(29)已是可积的n阶常数系数线性微分方程。再由双变换(27),可知n阶变系数非线性微分方程(26)可积。
, 百拇医药
当定理4中的n=4时,并由(28)可得
推论 若给定条件组
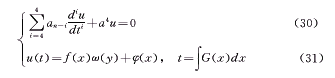
其中,G∈c3,f、ω、φ∈c4,f=f(x)≠0,φ=φ(x)≠0,G=G(x),ω(y)≠const,au=const,i=1,2,3,4,则可构造出可积的四阶变系数非线性微分方程:
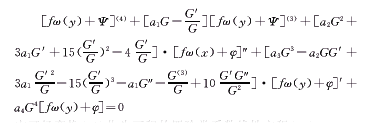 (32)
(32)它可经变换(31)化为可积的四阶常系数线性方程(30)。
注:本推论的后一部分,即为文献[4]中定理3.2所研究的情形。
定理5 若给定条件组
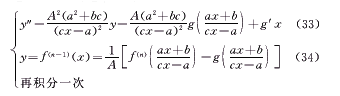
, 百拇医药
再积分一次
其中,f∈cn+1,g∈c,a、b、c、A均为常数,且A≠0,c≠0,a2+bc≠0,n为正整数,n≥1,还约定f(0)=f,则可构造出可积的常微分方程:
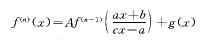 (35)
(35)证明 易知(33)是可积的二阶非齐次Euler(欧拉)方程,将(34)代入(33),再积分一次,可构造出可积的常微分方程(35)。
事实上,将双变换(34)代入(33),可得:

两边再积分一次得:
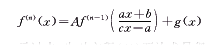
, 百拇医药
反过来,先对方程(35)两边求导得:
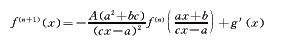 (36)
(36)再由(35)得变换:
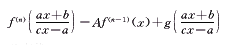 (37)
(37)及变换:
f(n-1)(x)=y (38)
将双变换(37)与(38)代入(36),整理后得:
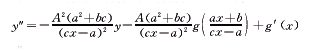
或
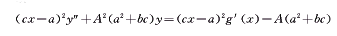
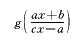
, http://www.100md.com
显然这已是可积的二阶非齐次Euler方程,将它的解代入变换(38)再积分n-1次,可知原方程(35)可积。
注:定理5的后一部分,即为文献[5]的定理1。
参 考 文 献
1,王高雄等编.常微分方程.第二版.北京:高等教育出版社,1983,36.
2,汤光宋.几类微分方程推广与求解.江汉大学学报,1990,7(1):47~53.
3,汤光宋.若干新的一阶变系数常微分方程的可积类型.江汉大学学报(自然科学版).1987,(1):18~26.
4,李恒祥.几类可积的非线性常微分方程(Ⅱ)—高阶方程.应用数学和力学.1990,11(6):521~527.
5,汤光宋.可积常微分方程的新类型.山东轻工业学院学报(自然科学版),1993,(1):71~73.
收稿日期:2000-03-21, http://www.100md.com