四格表两种合并方法等价点的计算与应用
作者:苏银法 杜乐燕
单位:苏银法(浙江省温州市医药科学研究所 温州325003);杜乐燕(温州医学院附一院)
关键词:
数理医药学杂志000408 中图分类号: R 311 文献标识码: B
文章编号:1004-4337(2000)04-0302-02
四格表的合并有两种常用的方法,即χ2值相加法(下称∑χ2法)和χ值相加法(下称∑χ法)。前文[1]主要讨论了这两种方法的不等价性,认为在大多数情况下,∑χ2法的统计推断相对较严,但也提出了这两种方法在统计学上存在等P值法。本文主要讨论等P值的计算问题,以及应用等P值点的有关参数,快速判断两种合并方法对统计结论的影响。
, http://www.100md.com
1 计算等价点的数理基础
∑χ2法的计算公式为: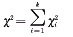 自由度f=k
自由度f=k
∑χ法的计算公式为: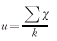 自由度f=1
自由度f=1
前文认为[1],四格表的合并要进行χ2的非均匀性检验,即: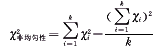 自由度f=k-1
自由度f=k-1
文献[1]中的ε值与非均匀性检验的χ2值完全等价,若ε≥χ20.05(f),则各四格表不宜合并。
, 百拇医药
根据文献[2]中的χ2值直接求P值的计算公式,采用逐步逼近法求∑χ2法和∑χ法的等P值点,表1所列为两个四格表合并时,两种合并方法逼近等P值点的过程,结果χ21=1时,等P值点为P=0.0037,χ21=10.2。
表1 逐步逼近法求四格表两种合并方法的等P值点(χ21=1) 合并方法
χ22
9
10
11
10.4
, http://www.100md.com
10.2
∑χ2法
0.0067
0.0041
0.0025
0.0033
0.0037
∑χ法
0.0055
0.0031
0.0029
0.0035
, 百拇医药
0.0037
2 两种合并方法等价点的计算
据上所述,可对多个四格表的不同χ2值计算等价点。方法是:若两个四格表合并,先给定χ21(三个四格表合并则先给定χ21和χ22,余类推),在计算机辅助下,输入χ21及等价点χ22的初值,计算机自动按逐步逼近法给出等P值点的χ22值、P值及ε值。本文仅列表2、表3给出部分计算结果。应用时既可直接查表,也可由计算机十分方便地求得等P值点的各参数值。
表2 两个四格表合并时两种合并方法的等P值点 χ21
, http://www.100md.com
χ22
P
ε
0
3.0492
0.21771
1.5246
0.25
6.7985
0.02947
2.2206
0.50
, http://www.100md.com
8.2720
0.01245
2.3523
0.75
9.3495
0.006411
2.4017
1.00
10.2120
0.003676
2.4104
表3 三个四格表合并时两种合并方法的等P值点 χ21=0
, 百拇医药
χ21=0.25
χ21=0.50
χ21=0.75
χ22
χ23
P×102
ε
χ22
χ23
, 百拇医药
P×102
ε
χ22
χ23
P×102
ε
χ22
χ23
P×102
ε
, 百拇医药
0
4.31
23.14
2.8733
0.25
6.6018
7.7842
3.7114
0.25
9.3223
20.6400
4.3460
0.50
, 百拇医药
7.3587
4.9870
3.9604
0.50
10.2546
12.0540
4.5237
0.50
11.250
6.8130
4.6711
0.75
, http://www.100md.com 7.8629
3.5606
4.1230
0.75
10.8900
8.0380
4.6327
0.75
11.931
4.4380
4.7566
0.75
12.645
, 百拇医药
2.8430
4.8239
1.00
8.2342
2.6926
4.2341
1.00
11.3690
5.7500
4.7075
1.00
12.448
3.1140
, 百拇医药
4.8120
1.00
13.188
1.9690
4.8636
1.25
8.5188
2.1146
4.3371
1.25
11.7480
4.3030
4.7621
, 百拇医药
1.25
12.859
2.2940
4.8490
1.25
13.620
1.4350
4.8864
1.50
8.7408
1.7070
4.4132
1.50
, 百拇医药
12.0550
3.3270
4.8028
1.50
13.192
1.7500
4.8729
1.50
13.974
1.0840
4.8984
1.75
8.9145
, 百拇医药
1.4077
4.4765
1.75
12.3060
2.6390
4.8303
1.75
13.470
1.3700
4.8895
1.75
14.271
0.8410
, 百拇医药
4.9042
2.00
9.0480
1.1817
4.5294
2.00
12.5140
2.1350
4.8569
2.00
13.698
1.0970
4.8979
, 百拇医药
2.00
14.513
0.6690
4.9010
3 等价点的应用
3.1 等P值点χ2值的应用 根据等P值点的χ2值,判断给出的χ21、χ22(指两个四格表合并)经两法统计处理后将会得到怎样的统计推断结果。例如:四格表的χ21=0.75,χ22=5,查表2,χ2=0.75时,等P值点的χ22(即χ22e)=9.3495,可见χ22<χ22e。由文献[1]的讨论可知,∑χ2法将会得出相对较严的统计推断结果或相对较大的P值。
, 百拇医药
3.2 等P值点P值的应用 当等P值点的P值约等于0.05时,首先按给定的一个χ2(即二个四格表合并)查表2中相应的χ2值(由微机完成),然后根据另一χ2值是大于或是小于等P值点的另一χ2值,直接判断四格表合并后其P值是大于或小于0.05。
3.3 等P值点ε值的应用 当等P值点的ε值等于四格表非均匀性检验的χ20.05(f)时,按3.2中的方法,根据另一χ2值是否小于等P值点的另一χ2值,直接判断各四格表能否合并。
4 讨论
本文通过统计模型,肯定了文献[1]提出的∑χ法的统计推断相对较宽这一结论,不过从表2、表3中可以发现,两法的统计结论大多为P<0.05,从这一角度来说,实际应用时若各四格表的方向一致,任选一种统计方法基本上是可行的。
, 百拇医药
尽管表3中ε值与P值间的变化有一定的规律,如等P值点的ε值越大,P值越小。但也不尽然,如末行ε=4.9010、P=0.6690013×10-3就不符合这一规律。事实上,尚有许多这类情况表3未予列出。出现这一情况,究其原因,是因为ε值代表了各χ2值的离均差平方和,它与各χ2的离散程度有关;而P值与∑χ2或∑χ值的大小有关,而与ε值无直接关系。
参 考 文 献
1,苏银法.实例分析四格表两种合并方法的不等价性.数理医药学杂志,1994,7(3):248.
2,金丕焕,黄小兰,史秉璋,等.医用统计程序集.上海科学技术出版社,1996,326~329.
收稿日期:1999-07-20, http://www.100md.com
单位:苏银法(浙江省温州市医药科学研究所 温州325003);杜乐燕(温州医学院附一院)
关键词:
数理医药学杂志000408 中图分类号: R 311 文献标识码: B
文章编号:1004-4337(2000)04-0302-02
四格表的合并有两种常用的方法,即χ2值相加法(下称∑χ2法)和χ值相加法(下称∑χ法)。前文[1]主要讨论了这两种方法的不等价性,认为在大多数情况下,∑χ2法的统计推断相对较严,但也提出了这两种方法在统计学上存在等P值法。本文主要讨论等P值的计算问题,以及应用等P值点的有关参数,快速判断两种合并方法对统计结论的影响。
, http://www.100md.com
1 计算等价点的数理基础
∑χ2法的计算公式为:
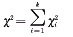 自由度f=k
自由度f=k∑χ法的计算公式为:
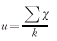 自由度f=1
自由度f=1前文认为[1],四格表的合并要进行χ2的非均匀性检验,即:
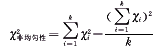 自由度f=k-1
自由度f=k-1文献[1]中的ε值与非均匀性检验的χ2值完全等价,若ε≥χ20.05(f),则各四格表不宜合并。
, 百拇医药
根据文献[2]中的χ2值直接求P值的计算公式,采用逐步逼近法求∑χ2法和∑χ法的等P值点,表1所列为两个四格表合并时,两种合并方法逼近等P值点的过程,结果χ21=1时,等P值点为P=0.0037,χ21=10.2。
表1 逐步逼近法求四格表两种合并方法的等P值点(χ21=1) 合并方法
χ22
9
10
11
10.4
, http://www.100md.com
10.2
∑χ2法
0.0067
0.0041
0.0025
0.0033
0.0037
∑χ法
0.0055
0.0031
0.0029
0.0035
, 百拇医药
0.0037
2 两种合并方法等价点的计算
据上所述,可对多个四格表的不同χ2值计算等价点。方法是:若两个四格表合并,先给定χ21(三个四格表合并则先给定χ21和χ22,余类推),在计算机辅助下,输入χ21及等价点χ22的初值,计算机自动按逐步逼近法给出等P值点的χ22值、P值及ε值。本文仅列表2、表3给出部分计算结果。应用时既可直接查表,也可由计算机十分方便地求得等P值点的各参数值。
表2 两个四格表合并时两种合并方法的等P值点 χ21
, http://www.100md.com
χ22
P
ε
0
3.0492
0.21771
1.5246
0.25
6.7985
0.02947
2.2206
0.50
, http://www.100md.com
8.2720
0.01245
2.3523
0.75
9.3495
0.006411
2.4017
1.00
10.2120
0.003676
2.4104
表3 三个四格表合并时两种合并方法的等P值点 χ21=0
, 百拇医药
χ21=0.25
χ21=0.50
χ21=0.75
χ22
χ23
P×102
ε
χ22
χ23
, 百拇医药
P×102
ε
χ22
χ23
P×102
ε
χ22
χ23
P×102
ε
, 百拇医药
0
4.31
23.14
2.8733
0.25
6.6018
7.7842
3.7114
0.25
9.3223
20.6400
4.3460
0.50
, 百拇医药
7.3587
4.9870
3.9604
0.50
10.2546
12.0540
4.5237
0.50
11.250
6.8130
4.6711
0.75
, http://www.100md.com 7.8629
3.5606
4.1230
0.75
10.8900
8.0380
4.6327
0.75
11.931
4.4380
4.7566
0.75
12.645
, 百拇医药
2.8430
4.8239
1.00
8.2342
2.6926
4.2341
1.00
11.3690
5.7500
4.7075
1.00
12.448
3.1140
, 百拇医药
4.8120
1.00
13.188
1.9690
4.8636
1.25
8.5188
2.1146
4.3371
1.25
11.7480
4.3030
4.7621
, 百拇医药
1.25
12.859
2.2940
4.8490
1.25
13.620
1.4350
4.8864
1.50
8.7408
1.7070
4.4132
1.50
, 百拇医药
12.0550
3.3270
4.8028
1.50
13.192
1.7500
4.8729
1.50
13.974
1.0840
4.8984
1.75
8.9145
, 百拇医药
1.4077
4.4765
1.75
12.3060
2.6390
4.8303
1.75
13.470
1.3700
4.8895
1.75
14.271
0.8410
, 百拇医药
4.9042
2.00
9.0480
1.1817
4.5294
2.00
12.5140
2.1350
4.8569
2.00
13.698
1.0970
4.8979
, 百拇医药
2.00
14.513
0.6690
4.9010
3 等价点的应用
3.1 等P值点χ2值的应用 根据等P值点的χ2值,判断给出的χ21、χ22(指两个四格表合并)经两法统计处理后将会得到怎样的统计推断结果。例如:四格表的χ21=0.75,χ22=5,查表2,χ2=0.75时,等P值点的χ22(即χ22e)=9.3495,可见χ22<χ22e。由文献[1]的讨论可知,∑χ2法将会得出相对较严的统计推断结果或相对较大的P值。
, 百拇医药
3.2 等P值点P值的应用 当等P值点的P值约等于0.05时,首先按给定的一个χ2(即二个四格表合并)查表2中相应的χ2值(由微机完成),然后根据另一χ2值是大于或是小于等P值点的另一χ2值,直接判断四格表合并后其P值是大于或小于0.05。
3.3 等P值点ε值的应用 当等P值点的ε值等于四格表非均匀性检验的χ20.05(f)时,按3.2中的方法,根据另一χ2值是否小于等P值点的另一χ2值,直接判断各四格表能否合并。
4 讨论
本文通过统计模型,肯定了文献[1]提出的∑χ法的统计推断相对较宽这一结论,不过从表2、表3中可以发现,两法的统计结论大多为P<0.05,从这一角度来说,实际应用时若各四格表的方向一致,任选一种统计方法基本上是可行的。
, 百拇医药
尽管表3中ε值与P值间的变化有一定的规律,如等P值点的ε值越大,P值越小。但也不尽然,如末行ε=4.9010、P=0.6690013×10-3就不符合这一规律。事实上,尚有许多这类情况表3未予列出。出现这一情况,究其原因,是因为ε值代表了各χ2值的离均差平方和,它与各χ2的离散程度有关;而P值与∑χ2或∑χ值的大小有关,而与ε值无直接关系。
参 考 文 献
1,苏银法.实例分析四格表两种合并方法的不等价性.数理医药学杂志,1994,7(3):248.
2,金丕焕,黄小兰,史秉璋,等.医用统计程序集.上海科学技术出版社,1996,326~329.
收稿日期:1999-07-20, http://www.100md.com