用EXCEL实现灰色数列模型GM(1,1)的预测
作者:李秀央 李振洪 蔡雪霞
单位:李秀央(浙江大学湖滨校区卫生统计教研室 杭州310031);李振洪(武汉测绘科技大学);蔡雪霞(浙江大学医学院第一附属医院)
关键词:灰色数列模型GM(1;1);EXCEL 预测;CM(1;1)程序
数理医药学杂志000405
摘 要 在编制好的GM(1,1)电子表格中输入已知时刻的实际数,就可以得到所需的目标时刻的预测值,并且可以得到对此模型预测的精确度检验结果。为灰色数列模型GM(1,1)的预测提供一种操作简便、精确度高的行之有效的方法,充分发挥了EXCEL电子表格的动态功能,具有简单易行的特点,有较大的推广应用价值。
中图分类号: O 159 文献标识码: A
, http://www.100md.com
文章编号:1004-4337(2000)04-0296-02
灰色数列模型(Grey Dynamics Model,GM)是以时间序列进行研究分析,用数列建立方程,将无规律的原始数列经过转换,使之成为较有规律的生成数列后再建模的一种预测方法。从实践工作经验、实际数据特征、时间序列图形、预测误差比较等方面综合分析,用灰色数列模型预测卫生人力的发展趋势较目前常用的预测方法为优[1]。其中较为简单的一种模型—采用一个变量的一阶微分方程GM(1,1)模型已经广泛应用于医学研究的许多领域之中进行预测。虽然用GM(1,1)模型进行预测,具有思路简单、数据单纯、运算简便等特点,但是在具体运用中,若用手工或借助计算机完成,工作量还是相当大的,并且易出差错。目前随着计算机的普及,我们完全可以根据自己的需要用EXCEL自编一个电子表格,来完成GM(1,1)模型的预测。本文以浙江省1994~1997年的卫生技术人员的资料进行1998~2010年的预测为例,介绍用EXCEL来实现GM(1,1)模型的预测方法。
, 百拇医药
1 资料和方法
1.1 资料来源
1998年6月份第二次国家卫生服务总调查的浙江省11个县(市区)、90个乡镇(街道)的卫生机构卫生人力资源的数据资料。
1.2 灰色数列模型GM(1,1)预测方法
设原始数列排成时间数列Xt(t=0,1,2,…,n),其中Xt表示第t时刻的原始数列。
1.2.1 累加生成
通常原始数据呈现离乱现象,灰色理论将无规律的原始数据按(1)式累加生成,使其变为较有规律的生成数列Yt。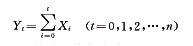 (1)
(1)
, http://www.100md.com
1.2.2 移动平均数生成
对累加生成数据Yt按式(2)作移动平均数生成Zt。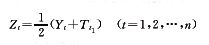 (2)
(2)
1.2.3 建立模型GM(1,1)
Yt的一阶线性微分方程为: (3)
(3)
(3)式即为GM(1,1)模型,其中α、μ为特定系数。
按微分方程的求解方法得到: (4)
(4)
, 百拇医药
其中X0为初始时刻的原始数据。根据最小二乘法估计参数得: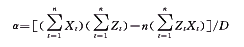 (5)
(5)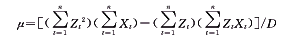 (6)
(6)
其中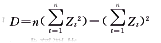 (7)
(7)
1.2.4 求预测值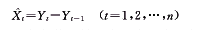 (8)
(8)
因灰色数列模型实际上是生成数列模型,对累加生成数据必须经过逆生成—累减还原后才能使用,即GM(1,1)模型计算所得结果是预测值的累加和,故预测值由上式计算可得。
1.2.5 计算后验差比值C
, http://www.100md.com
① 计算残差δ及δ的样本总体的标准偏差S1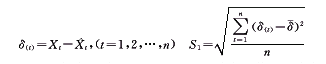
② 计算实际数Xt(1,2,…,n)的样本总体的标准偏差S2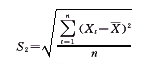
③ 计算C值
C=S1/S2, C值是进行预测精确度检验的统计量。
1.2.6 外推预测
按式(4)、(8)进行。
1.3 建立电子表格
, http://www.100md.com
1.3.1 调整电子表格的结构,如表1所示。
1.3.2 输入原始数据 即1994~1997年的浙江省卫生技术人员的实际数和年份。
1.3.3 编程
① 计算累加生成Yt(t=0,1,2,…,n)、移动平均数生成Zt以及Zt2和ZtXt(t=1,2,…,n)
方法:先输入D3=C3,D4=D3+C4,E4=(1)/(2)(D3+D4),F4=POEWR(E4,2),G4=E4×C4,然后同时选中D4、E4、F4、G4,将之内容往下复制两行(即已知年份对应的行)。
② 计算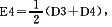
, 百拇医药
方法:输入C7=SUM(C4:C6),E7=SUM(E4:E6),F7=SUM(F4:F6),G7=SUM(G4:G6)。
③ 按公式(7)、(5)、(6)分别计算D、α、μ
方法:输入D10=ROUND((B6×F7-POWER(E7,2)),4),E10=ROUND((C7×E7-B6×G7)/D10,4),F10=ROUND((F7×C7-E7×G7)/D10,4)。
④ 按公式(4)、(8)计算Yt、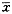 t
t
方法:先输入H4=ROUND((C3-F10/E10)×EXP(-E10×B4)+F10/E10,0),I4=H4-H3,然后选中H4、I4,再将之内容往下复制两行(注:H3内容可以由H4复制而得)。
, 百拇医药
⑤ 计算实际值与预测值的残差δ和残差均数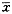 以及残差样本总体标准差S1
以及残差样本总体标准差S1
方法:输入J4=C4-I4,J8=ROUND (AVERAGE (J4:J6),4),J10=ROUND (STDEVP (J4:J6),4),并且将J4内容往下复制两个格子。
⑥ 计算已知年份中非出始年份的实际数的样本总体标准差S2和后验差比值C
方法:输入C12=ROUND (STDEVP (C4:C6),4),J13=ROUND (J10/C12,2)。
⑦ 计算|δ(t)-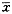 |和0.6745S2
|和0.6745S2
, 百拇医药
方法:输入J15=ROUND (ABS(J4-J8),2),J19-ROUND(0.6745×C12,2),再将J15的内容往下复制两格。经过以上几步,就可得到一张GM(1,1)的电子表格。
2 结果
只要输入1994~1997年的实际数,就可以得到目标年份的预测值和预测精确度的检验结果,见表1。
表1 浙江省卫生技术人员的预测 A
B
C
D
E
F
G
, 百拇医药
H
I
J
年份
t
Xt
Yt
Zt
Zt2
ZtXt
yt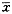 t
t
, 百拇医药
后验差检验
1994
0
33404
33404
33404
残差(δ)
1995
1
33946
67350
50377
253784212
, 百拇医药
171009764
67312
33908
38
1996
2
35169
102519
84934.5
7213869290
2987061431
102543
, http://www.100md.com 35231
-62
1997
3
35543
139162
120840.5
14602426440
4427958442
139150
36607
36
1998
, 百拇医药
4
105758
256152
243541378
912511751
177186
38036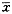
1999
5
216708
39522
, http://www.100md.com 4
2000
6
D
α
μ
257772
41064
S1
2001
7
7448566475
-0.0383
, http://www.100md.com
31983.0415
300439
42667
46.6762
2002
8
S2
344773
44334
2003
9
1102.633
, http://www.100md.com 390837
46064
C=S1/S2
2004
10
438700
47863
0.04
2005
11
488432
49732
, 百拇医药
|δ(t)-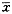 |
|
2006
12
540105
51673
34
2007
13
593795
53690
66
2008
, 百拇医药
14
649582
55787
32
2009
15
707547
57965
0.6745S2
2010
16
767775
60228
, 百拇医药
743.73
3 讨论
3.1 用EXCEL编制的GM(1,1)模型电子表格是一张动态的电子表格,对相同已知时刻点的资料,其对应EXCEL电子表格可以设计相同。因此进行预测时,只要输入已知时刻点的实际数,就可以得出所需的结果,使用起来相当便利。当然,如果已知时刻数不同,其电子表格的格式和程序应作相应的改动,改动方法较简单,以建模方法中的计算公式为依据。
3.2 灰色数列模型对样本含量和概率分布没有严格的要求,且本身已考虑到其它多种因素的影响,加之数据单纯、运算简便,具有简单易行的特点。不少专家认为数学模型法是最有发展前途的预测方法之一[2],而本文介绍的GM(1,1)模型是其中方法之一,因此,它是值得推广的一种预测工具。
参 考 文 献
1,关欣,谭兆印,李斌等.卫生人力预测—灰色模型预测.中国社会医学1992,(5):13~15.
2,马材芳.江苏省卫生人力预测—灰色模型预测.中国卫生经济,1989,(7):31~35.
收稿日期:1999-12-18, 百拇医药
单位:李秀央(浙江大学湖滨校区卫生统计教研室 杭州310031);李振洪(武汉测绘科技大学);蔡雪霞(浙江大学医学院第一附属医院)
关键词:灰色数列模型GM(1;1);EXCEL 预测;CM(1;1)程序
数理医药学杂志000405
摘 要 在编制好的GM(1,1)电子表格中输入已知时刻的实际数,就可以得到所需的目标时刻的预测值,并且可以得到对此模型预测的精确度检验结果。为灰色数列模型GM(1,1)的预测提供一种操作简便、精确度高的行之有效的方法,充分发挥了EXCEL电子表格的动态功能,具有简单易行的特点,有较大的推广应用价值。
中图分类号: O 159 文献标识码: A
, http://www.100md.com
文章编号:1004-4337(2000)04-0296-02
灰色数列模型(Grey Dynamics Model,GM)是以时间序列进行研究分析,用数列建立方程,将无规律的原始数列经过转换,使之成为较有规律的生成数列后再建模的一种预测方法。从实践工作经验、实际数据特征、时间序列图形、预测误差比较等方面综合分析,用灰色数列模型预测卫生人力的发展趋势较目前常用的预测方法为优[1]。其中较为简单的一种模型—采用一个变量的一阶微分方程GM(1,1)模型已经广泛应用于医学研究的许多领域之中进行预测。虽然用GM(1,1)模型进行预测,具有思路简单、数据单纯、运算简便等特点,但是在具体运用中,若用手工或借助计算机完成,工作量还是相当大的,并且易出差错。目前随着计算机的普及,我们完全可以根据自己的需要用EXCEL自编一个电子表格,来完成GM(1,1)模型的预测。本文以浙江省1994~1997年的卫生技术人员的资料进行1998~2010年的预测为例,介绍用EXCEL来实现GM(1,1)模型的预测方法。
, 百拇医药
1 资料和方法
1.1 资料来源
1998年6月份第二次国家卫生服务总调查的浙江省11个县(市区)、90个乡镇(街道)的卫生机构卫生人力资源的数据资料。
1.2 灰色数列模型GM(1,1)预测方法
设原始数列排成时间数列Xt(t=0,1,2,…,n),其中Xt表示第t时刻的原始数列。
1.2.1 累加生成
通常原始数据呈现离乱现象,灰色理论将无规律的原始数据按(1)式累加生成,使其变为较有规律的生成数列Yt。
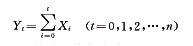 (1)
(1), http://www.100md.com
1.2.2 移动平均数生成
对累加生成数据Yt按式(2)作移动平均数生成Zt。
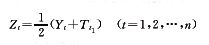 (2)
(2)1.2.3 建立模型GM(1,1)
Yt的一阶线性微分方程为:
 (3)
(3)(3)式即为GM(1,1)模型,其中α、μ为特定系数。
按微分方程的求解方法得到:
 (4)
(4), 百拇医药
其中X0为初始时刻的原始数据。根据最小二乘法估计参数得:
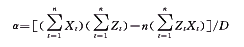 (5)
(5)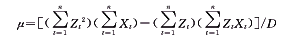 (6)
(6)其中
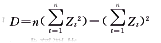 (7)
(7)1.2.4 求预测值
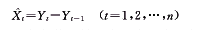 (8)
(8)因灰色数列模型实际上是生成数列模型,对累加生成数据必须经过逆生成—累减还原后才能使用,即GM(1,1)模型计算所得结果是预测值的累加和,故预测值由上式计算可得。
1.2.5 计算后验差比值C
, http://www.100md.com
① 计算残差δ及δ的样本总体的标准偏差S1
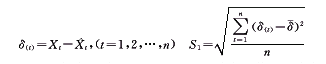
② 计算实际数Xt(1,2,…,n)的样本总体的标准偏差S2
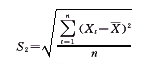
③ 计算C值
C=S1/S2, C值是进行预测精确度检验的统计量。
1.2.6 外推预测
按式(4)、(8)进行。
1.3 建立电子表格
, http://www.100md.com
1.3.1 调整电子表格的结构,如表1所示。
1.3.2 输入原始数据 即1994~1997年的浙江省卫生技术人员的实际数和年份。
1.3.3 编程
① 计算累加生成Yt(t=0,1,2,…,n)、移动平均数生成Zt以及Zt2和ZtXt(t=1,2,…,n)
方法:先输入D3=C3,D4=D3+C4,E4=(1)/(2)(D3+D4),F4=POEWR(E4,2),G4=E4×C4,然后同时选中D4、E4、F4、G4,将之内容往下复制两行(即已知年份对应的行)。
② 计算
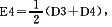
, 百拇医药
方法:输入C7=SUM(C4:C6),E7=SUM(E4:E6),F7=SUM(F4:F6),G7=SUM(G4:G6)。
③ 按公式(7)、(5)、(6)分别计算D、α、μ
方法:输入D10=ROUND((B6×F7-POWER(E7,2)),4),E10=ROUND((C7×E7-B6×G7)/D10,4),F10=ROUND((F7×C7-E7×G7)/D10,4)。
④ 按公式(4)、(8)计算Yt、
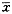 t
t方法:先输入H4=ROUND((C3-F10/E10)×EXP(-E10×B4)+F10/E10,0),I4=H4-H3,然后选中H4、I4,再将之内容往下复制两行(注:H3内容可以由H4复制而得)。
, 百拇医药
⑤ 计算实际值与预测值的残差δ和残差均数
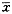 以及残差样本总体标准差S1
以及残差样本总体标准差S1方法:输入J4=C4-I4,J8=ROUND (AVERAGE (J4:J6),4),J10=ROUND (STDEVP (J4:J6),4),并且将J4内容往下复制两个格子。
⑥ 计算已知年份中非出始年份的实际数的样本总体标准差S2和后验差比值C
方法:输入C12=ROUND (STDEVP (C4:C6),4),J13=ROUND (J10/C12,2)。
⑦ 计算|δ(t)-
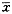 |和0.6745S2
|和0.6745S2, 百拇医药
方法:输入J15=ROUND (ABS(J4-J8),2),J19-ROUND(0.6745×C12,2),再将J15的内容往下复制两格。经过以上几步,就可得到一张GM(1,1)的电子表格。
2 结果
只要输入1994~1997年的实际数,就可以得到目标年份的预测值和预测精确度的检验结果,见表1。
表1 浙江省卫生技术人员的预测 A
B
C
D
E
F
G
, 百拇医药
H
I
J
年份
t
Xt
Yt
Zt
Zt2
ZtXt
yt
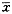 t
t, 百拇医药
后验差检验
1994
0
33404
33404
33404
残差(δ)
1995
1
33946
67350
50377
253784212
, 百拇医药
171009764
67312
33908
38
1996
2
35169
102519
84934.5
7213869290
2987061431
102543
, http://www.100md.com 35231
-62
1997
3
35543
139162
120840.5
14602426440
4427958442
139150
36607
36
1998
, 百拇医药
4
105758
256152
243541378
912511751
177186
38036
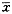
1999
5
216708
39522
, http://www.100md.com 4
2000
6
D
α
μ
257772
41064
S1
2001
7
7448566475
-0.0383
, http://www.100md.com
31983.0415
300439
42667
46.6762
2002
8
S2
344773
44334
2003
9
1102.633
, http://www.100md.com 390837
46064
C=S1/S2
2004
10
438700
47863
0.04
2005
11
488432
49732
, 百拇医药
|δ(t)-
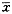 |
|2006
12
540105
51673
34
2007
13
593795
53690
66
2008
, 百拇医药
14
649582
55787
32
2009
15
707547
57965
0.6745S2
2010
16
767775
60228
, 百拇医药
743.73
3 讨论
3.1 用EXCEL编制的GM(1,1)模型电子表格是一张动态的电子表格,对相同已知时刻点的资料,其对应EXCEL电子表格可以设计相同。因此进行预测时,只要输入已知时刻点的实际数,就可以得出所需的结果,使用起来相当便利。当然,如果已知时刻数不同,其电子表格的格式和程序应作相应的改动,改动方法较简单,以建模方法中的计算公式为依据。
3.2 灰色数列模型对样本含量和概率分布没有严格的要求,且本身已考虑到其它多种因素的影响,加之数据单纯、运算简便,具有简单易行的特点。不少专家认为数学模型法是最有发展前途的预测方法之一[2],而本文介绍的GM(1,1)模型是其中方法之一,因此,它是值得推广的一种预测工具。
参 考 文 献
1,关欣,谭兆印,李斌等.卫生人力预测—灰色模型预测.中国社会医学1992,(5):13~15.
2,马材芳.江苏省卫生人力预测—灰色模型预测.中国卫生经济,1989,(7):31~35.
收稿日期:1999-12-18, 百拇医药