秩和比综合评价方法在食品卫生方面的应用
作者:姜小红 杭洋 张瑞明 田继瑞 麻旭红
单位:姜小红(太原市卫生防疫站 030012);杭洋(太原市卫生防疫站 030012);张瑞明(太原市卫生防疫站 030012);田继瑞(太原市卫生监督站);麻旭红(太原市卫生监督站)
关键词:
山西医药杂志000545 建国50 a来,我国广大食品卫生工作者在保证食品的营养和卫生方面做了大量的工作。国家 也相继颁布实施了约200余项《食品卫生标准》,这些《标准》的颁布实施,对于我们正确 地评价、判定食品的卫生质量,保障广大人民群众身体健康都起到了积极的作用。传统的评 价方法是以单一的评价指标检测结果与相应标准进行比较,判定其是否达标,但这些分散、 单一的评价指标难以从整体的角度,对食品的卫生质量做出全面、客观、合理的综合评价。 笔者带着这些问题,在查阅了大量相关文献的基础上,将秩和比(RSR)法[1,2]用 于食品卫生质量评价。旨在从整体的角度全面、客观、合理地综合评价食品卫生质量。
, http://www.100md.com
1 资料来源
1999年太原市卫生防疫站对全市酸牛奶抽检结果,见表1。
表1 太原市10家酸牛奶生产厂样品抽检结果及RS R值 生产
厂家
大肠菌群
致病菌
脂肪
全乳固体
蛋白质
砂糖
汞
RSR=(ER)/(n=10×7=70)
, http://www.100md.com
国标(个/100mL)
结果
秩序
国标
结果
秩序
国标%
结果
秩序
国标%
结果
秩序
国标%
, http://www.100md.com
结果
秩序
国标%
结果
秩序
国标(以Hg计)10-6
结果
秩序
A
≤90
24 000
2
未检出
, 百拇医药
未检出
5.5
≥3
2.86
1
≥11.5
11.12
2
70.00~110.00
57.78
3
≥5
6.12
, 百拇医药
8
≤0.01
≤0.01
5.5
0.385 7
B
≤90
190
5
未检出
未检出
5.5
≥3
, 百拇医药
2.93
3
≥11. 5
11.17
3
70.00~110.00
119.8
6
≥5
5.34
2
≤0. 01
≤0.01
, 百拇医药
5.5
0.428 6
C
≤90
2 400
3.5
未检出
未检出
5.5
≥3
2.90
2
≥11.5
, http://www.100md.com
11.24
4
70.00~110.00
57.83
4
≥5
5.17
1
≤0.01
≤0.01
5.5
0.364 2
D
, 百拇医药
≤90
≤30
8.5
未检出
未检出
5.5
≥3
3.09
9
≥ 11.5
11.70
9
70.00~110.00
, http://www.100md.com
94.16
9
≥5
6.20
9.5
≤0.01
≤0.01
5.5
0.800 0
E
≤90
≤30
8.5
, 百拇医药
未检出
未检出
5.5
≥3
3.11
10
≥11.5
11.80
10
70.00~110.00
92.02
10
≥5
, http://www.100md.com
6.20
9.5
≤0.01
≤0.01
5.5
0.842 9
F
≤90
2 400
3.5
未检出
未检出
5.5
, 百拇医药
≥3
3.02
6.5
≥11.5
11.35
5
70.00~110.00
53.50
2
≥5
5.67
5
≤0.01
, 百拇医药
≤0.01
5.5
0.471 4
G
≤90
>24 000
1
未检出
未检出
5.5
≥3
3.02
6.5
, 百拇医药
≥11.5
11.47
7
70.00~110.00
104.86
7
≥5
5.47
4
≤0.01
≤0.01
5.5
0.521 4
, http://www.100md.com
H
≤90
90
6.5
未检出
未检出
5.5
≥3
2.95
4
≥11 .5
11.43
6
, 百拇医药
70.00~110.00
96.30
8
≥5
5.96
6
≤0 .01
≤0.01
5.5
0.592 9
I
≤90
<3
, 百拇医药
10
未检出
未检出
5.5
≥3
3.08
8
≥11 .5
11.54
8
70.00~110.00
47.28
1
, http://www.100md.com
≥5
6.08
7
≤0 .01
≤0.01
5.5
0.624 9
J
≤90
90
6.5
未检出
未检出
, 百拇医药
5.5
≥3
3.01
5
≥11 .5
4.57
1
70.00~110.00
70.62
5
≥5
5.45
3
, http://www.100md.com
≤0 .01
≤0.01
5.5
0.450 0
2 方法介绍
①计算RSR值。②确定RSR分布,见表2。③进行合理的分档与排序。根据文献[1]中提供的 合理分档数表(标准档)进行合理分档。④进行最佳分档[2]。其准则是:每档至少 2例,多分几组,参与合理分档表,反复试验,以达到最佳分档。表2 RSR的分布 RSR
f
f↓(R)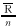 ×100%
×100%
, 百拇医药
Y (概率单位)
0.364 3
1
1
10
3.718 4
0.385 7
1
2
20
4.158 4
0.428 6
1
, http://www.100md.com
3
30
4.475 6
0.450 0
1
4
40
4.746 7
0.471 4
1
5
50
5.000 0
, 百拇医药
0.521 4
1
6
60
5.253 3
0.592 9
1
7
70
5.524 4
0.624 9
1
8
, 百拇医药
80
5.841 6
0.800 0
1
9
90
6.281 6
0.842 9
1
n=10
97.51)
6.960 0
1) 为(1-1/4n)的估计值。
, 百拇医药
3 结 果
3.1 太原市酸牛奶抽检结果的RSR值结果:见表1。
3.2 确定RSR分布:结果见表3。以概率单位Y为自变量。RSR为应变 量,求得直线回归方程[3]为RSR=-0.294 4+0.163 1Y
按V=n-2,得t=11.6,查界值表,P<0.01。r=0.971 8,RSR呈正态分 布。
3.3 合理分档与排序:结果见表3。
Bartlett检验: =0.002 054 286
=0.002 054 286
M=0.149 573 855 C=1.607 142 857
, 百拇医药
χ2=0.118,χ2(0.05,2)=10.60
P>0.05,方差一致。
ANOV:F=57.5 F0.05(7.2)=19
P<0.05,各档间相差显著。
表3 太原市10家酸牛奶生产厂样品抽检结果合理 分档 Y
分档
3.5以下
0.276 5以下
3.5~
, 百拇医药
0.276 5~
0.364 3(C)
0.385 7(A)
0.428 6(B)
0.450 0(J)
0.471 4(F)
5~
0.521 1~
0.624 9(I)
0.592 9(H)
0.521 4(G)
6.5~
, 百拇医药
0.765 8~
0.842 9(E)
0.800 0(D)
3.4 根据确定最佳分档的原则进行最佳分档:q检验结果见表4。两 两比较相差均显著。因此表3的合理分档达到了最佳分档。从表3可以看出:E、D生产的酸牛 奶卫生质量最好,I、H、G属中等,C、A、B、J、F较差。表4 合理分档q检验结果 对比组
A与B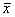 a-
a-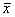 b
b
组数a
q值
, 百拇医药
P值
1与2
-0.159 7
2
6.738 4
<0.01
2与3
-0.241 8
2
7.980 0
<0.01
1与3
-0.401 5
, http://www.100md.com
3
14.494 6
<0.01
4 讨 论
本文是将秩和比(RSR)法应用于食品卫生质量综合评价的初次实践,经实例应用,其综合评 价结果较为理想。在众多的食品卫生质量评价指标中,大多数评价指标的检验结果为开口性 资料或文字描述性资料。这些检验结果用参数统计方法往往很难,甚至无法处理。非参数检 验的秩和比(RSR)法能较好地弥补这些缺点与不足[4]。在诸多评价指标中,每个评 价指标对综合评价的贡献各不相同,即有主要卫生指标和次要卫生指标之分。在对食品卫生 质量进行综合评价时,应充分考虑各评价指标的权重问题。本文是将RSR法应用于食品卫生 质量综合评价的初次实践,暂未考虑各评价指标的权重问题。如将其引入,该方法同样适用 。
, 百拇医药 (志谢:本文承太原市卫生防疫站金雪龙副主任医师指导、审阅,在此致谢)
作者简介:姜小红,女,1968年11月生,医师,太原市卫生防疫站,030012
参考文献
1.田风调.秩和比法及其运用.北京:中国统计出版社,1997.47
2.金雪龙.综合评价中分档数与分档界值确定方法的研究.山西医药杂志,1998, 27(3):199
3.蒋知俭.医学统计学.北京:人民卫生出版社,1997.121
4.郭秀花.秩和比综合评价在营养学方面的应用.中国卫生统计,1994,11(3):30
(收稿日期:2000-07-19), http://www.100md.com
单位:姜小红(太原市卫生防疫站 030012);杭洋(太原市卫生防疫站 030012);张瑞明(太原市卫生防疫站 030012);田继瑞(太原市卫生监督站);麻旭红(太原市卫生监督站)
关键词:
山西医药杂志000545 建国50 a来,我国广大食品卫生工作者在保证食品的营养和卫生方面做了大量的工作。国家 也相继颁布实施了约200余项《食品卫生标准》,这些《标准》的颁布实施,对于我们正确 地评价、判定食品的卫生质量,保障广大人民群众身体健康都起到了积极的作用。传统的评 价方法是以单一的评价指标检测结果与相应标准进行比较,判定其是否达标,但这些分散、 单一的评价指标难以从整体的角度,对食品的卫生质量做出全面、客观、合理的综合评价。 笔者带着这些问题,在查阅了大量相关文献的基础上,将秩和比(RSR)法[1,2]用 于食品卫生质量评价。旨在从整体的角度全面、客观、合理地综合评价食品卫生质量。
, http://www.100md.com
1 资料来源
1999年太原市卫生防疫站对全市酸牛奶抽检结果,见表1。
表1 太原市10家酸牛奶生产厂样品抽检结果及RS R值 生产
厂家
大肠菌群
致病菌
脂肪
全乳固体
蛋白质
砂糖
汞
RSR=(ER)/(n=10×7=70)
, http://www.100md.com
国标(个/100mL)
结果
秩序
国标
结果
秩序
国标%
结果
秩序
国标%
结果
秩序
国标%
, http://www.100md.com
结果
秩序
国标%
结果
秩序
国标(以Hg计)10-6
结果
秩序
A
≤90
24 000
2
未检出
, 百拇医药
未检出
5.5
≥3
2.86
1
≥11.5
11.12
2
70.00~110.00
57.78
3
≥5
6.12
, 百拇医药
8
≤0.01
≤0.01
5.5
0.385 7
B
≤90
190
5
未检出
未检出
5.5
≥3
, 百拇医药
2.93
3
≥11. 5
11.17
3
70.00~110.00
119.8
6
≥5
5.34
2
≤0. 01
≤0.01
, 百拇医药
5.5
0.428 6
C
≤90
2 400
3.5
未检出
未检出
5.5
≥3
2.90
2
≥11.5
, http://www.100md.com
11.24
4
70.00~110.00
57.83
4
≥5
5.17
1
≤0.01
≤0.01
5.5
0.364 2
D
, 百拇医药
≤90
≤30
8.5
未检出
未检出
5.5
≥3
3.09
9
≥ 11.5
11.70
9
70.00~110.00
, http://www.100md.com
94.16
9
≥5
6.20
9.5
≤0.01
≤0.01
5.5
0.800 0
E
≤90
≤30
8.5
, 百拇医药
未检出
未检出
5.5
≥3
3.11
10
≥11.5
11.80
10
70.00~110.00
92.02
10
≥5
, http://www.100md.com
6.20
9.5
≤0.01
≤0.01
5.5
0.842 9
F
≤90
2 400
3.5
未检出
未检出
5.5
, 百拇医药
≥3
3.02
6.5
≥11.5
11.35
5
70.00~110.00
53.50
2
≥5
5.67
5
≤0.01
, 百拇医药
≤0.01
5.5
0.471 4
G
≤90
>24 000
1
未检出
未检出
5.5
≥3
3.02
6.5
, 百拇医药
≥11.5
11.47
7
70.00~110.00
104.86
7
≥5
5.47
4
≤0.01
≤0.01
5.5
0.521 4
, http://www.100md.com
H
≤90
90
6.5
未检出
未检出
5.5
≥3
2.95
4
≥11 .5
11.43
6
, 百拇医药
70.00~110.00
96.30
8
≥5
5.96
6
≤0 .01
≤0.01
5.5
0.592 9
I
≤90
<3
, 百拇医药
10
未检出
未检出
5.5
≥3
3.08
8
≥11 .5
11.54
8
70.00~110.00
47.28
1
, http://www.100md.com
≥5
6.08
7
≤0 .01
≤0.01
5.5
0.624 9
J
≤90
90
6.5
未检出
未检出
, 百拇医药
5.5
≥3
3.01
5
≥11 .5
4.57
1
70.00~110.00
70.62
5
≥5
5.45
3
, http://www.100md.com
≤0 .01
≤0.01
5.5
0.450 0
2 方法介绍
①计算RSR值。②确定RSR分布,见表2。③进行合理的分档与排序。根据文献[1]中提供的 合理分档数表(标准档)进行合理分档。④进行最佳分档[2]。其准则是:每档至少 2例,多分几组,参与合理分档表,反复试验,以达到最佳分档。表2 RSR的分布 RSR
f
f↓(R)
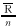 ×100%
×100%, 百拇医药
Y (概率单位)
0.364 3
1
1
10
3.718 4
0.385 7
1
2
20
4.158 4
0.428 6
1
, http://www.100md.com
3
30
4.475 6
0.450 0
1
4
40
4.746 7
0.471 4
1
5
50
5.000 0
, 百拇医药
0.521 4
1
6
60
5.253 3
0.592 9
1
7
70
5.524 4
0.624 9
1
8
, 百拇医药
80
5.841 6
0.800 0
1
9
90
6.281 6
0.842 9
1
n=10
97.51)
6.960 0
1) 为(1-1/4n)的估计值。
, 百拇医药
3 结 果
3.1 太原市酸牛奶抽检结果的RSR值结果:见表1。
3.2 确定RSR分布:结果见表3。以概率单位Y为自变量。RSR为应变 量,求得直线回归方程[3]为RSR=-0.294 4+0.163 1Y
按V=n-2,得t=11.6,查界值表,P<0.01。r=0.971 8,RSR呈正态分 布。
3.3 合理分档与排序:结果见表3。
Bartlett检验:
 =0.002 054 286
=0.002 054 286M=0.149 573 855 C=1.607 142 857
, 百拇医药
χ2=0.118,χ2(0.05,2)=10.60
P>0.05,方差一致。
ANOV:F=57.5 F0.05(7.2)=19
P<0.05,各档间相差显著。
表3 太原市10家酸牛奶生产厂样品抽检结果合理 分档 Y

分档
3.5以下
0.276 5以下
3.5~
, 百拇医药
0.276 5~
0.364 3(C)
0.385 7(A)
0.428 6(B)
0.450 0(J)
0.471 4(F)
5~
0.521 1~
0.624 9(I)
0.592 9(H)
0.521 4(G)
6.5~
, 百拇医药
0.765 8~
0.842 9(E)
0.800 0(D)
3.4 根据确定最佳分档的原则进行最佳分档:q检验结果见表4。两 两比较相差均显著。因此表3的合理分档达到了最佳分档。从表3可以看出:E、D生产的酸牛 奶卫生质量最好,I、H、G属中等,C、A、B、J、F较差。表4 合理分档q检验结果 对比组
A与B
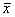 a-
a-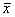 b
b组数a
q值
, 百拇医药
P值
1与2
-0.159 7
2
6.738 4
<0.01
2与3
-0.241 8
2
7.980 0
<0.01
1与3
-0.401 5
, http://www.100md.com
3
14.494 6
<0.01
4 讨 论
本文是将秩和比(RSR)法应用于食品卫生质量综合评价的初次实践,经实例应用,其综合评 价结果较为理想。在众多的食品卫生质量评价指标中,大多数评价指标的检验结果为开口性 资料或文字描述性资料。这些检验结果用参数统计方法往往很难,甚至无法处理。非参数检 验的秩和比(RSR)法能较好地弥补这些缺点与不足[4]。在诸多评价指标中,每个评 价指标对综合评价的贡献各不相同,即有主要卫生指标和次要卫生指标之分。在对食品卫生 质量进行综合评价时,应充分考虑各评价指标的权重问题。本文是将RSR法应用于食品卫生 质量综合评价的初次实践,暂未考虑各评价指标的权重问题。如将其引入,该方法同样适用 。
, 百拇医药 (志谢:本文承太原市卫生防疫站金雪龙副主任医师指导、审阅,在此致谢)
作者简介:姜小红,女,1968年11月生,医师,太原市卫生防疫站,030012
参考文献
1.田风调.秩和比法及其运用.北京:中国统计出版社,1997.47
2.金雪龙.综合评价中分档数与分档界值确定方法的研究.山西医药杂志,1998, 27(3):199
3.蒋知俭.医学统计学.北京:人民卫生出版社,1997.121
4.郭秀花.秩和比综合评价在营养学方面的应用.中国卫生统计,1994,11(3):30
(收稿日期:2000-07-19), http://www.100md.com