后遗障碍的模糊评价
作者：熊平 曾可先
单位：熊平(南华大学法医研究与鉴定中心，湖南衡阳 421001)；曾可先(衡阳市公安局刑侦技 术大队，湖南衡阳 421001)
关键词：后遗障碍；查德算子；广义模糊算子；多级模糊综合评判
川北医学院学报000443 摘 要：损伤给受损伤者带来或多或少的后遗障碍，在后遗障碍的评 定中，又受很多因素的影响，特别是这些因素在目前无法进行定量判定。本研究利用模糊综合评判对后遗障碍进行分级分度，以求指导损害赔偿，笔者简述了模糊综合评判模 型的基本概念和原理。同时，通过法医学实例介绍了该模型的应用。
中图分类号：D919 文献标 识码：E
文章编号：1005-3697(2000)04-0055-03
, 百拇医药
Blurred evaluation of injury extent
XIONG Ping ZENG Ke-xian
(Department of Forensic Medicine, South China University, Hengyang,Hu nan, 421001， China)
Abstract:The basic concept and principle of a model of blurre d synthet evaluation was introduced. A blurred syntheticl evaluation of grade a classification for the obstacle of sequelae was used to quide compensation harmn ess. The practice of this model was introduced by forensic medici examples.
, 百拇医药
Key words:blurred operator; blurred syntheticl appraise ev aluation; injury extent
在后遗障碍(残废)评定中，尽管国内外有不少种类的一览表，但每一种表都不能包罗万象。由于损伤的种类很多，再加上多重损伤的排列组 合，使得后遗障碍的类型很多，一览表上无法一一对号入座。在实际工作中往往都是以某地 、某些行政单位制定一览表作为判定的理论基础，由于人们的认识水平和实践经验不同，以 及实际处理结果上的差异，导致所制定的一览表也不尽相同。怎样评定后遗障碍并进行分度 ，我们已作了一些理论分析，对如何区别某一后遗障碍与另一后遗障碍两者的严重程度，特 别是在两种后遗障碍比较接近的情况下，怎样进行分级分度，这是我们一直研究的问题。由 于损伤造成的人身损害是多方面的，它包括生物属性的损害、社会属性的损害、精神心理的 损害、人际关系的损害。而这些方面又由很多因素所构成，所以对一个损伤应采取综合评价 。
, http://www.100md.com
所谓的综合评价就是对某一损伤程度进行全面而恰当的评价。要全面而恰当地评价损伤必须 从如下几个方面考虑：机体的完善性破坏、机体功能障碍、职业劳动能力的丧失、仪表完美 性损害、精神心理损害的程度、社会适应能力减少。又由于每个因素在评价中的“权数”不 尽相同，且评价指标间的关系错综复杂，表现的趋势不完全一致，所以收集到的信息也往往 具有不同程度的模糊性。因此，我们试图用模糊综合评价来进行后遗障碍的分级。
1 基本概念及原理
1.1 广义模糊算子
设：二元模糊关系矩阵
权数
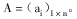那么，模糊综合评判
是在
下的合成运算，其中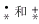
为广义模糊算子，常用的模型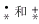有：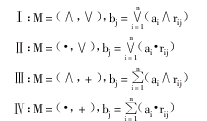
, 百拇医药
其中模型Ⅰ为Zade算子；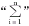
为n个数在+运算中求和；“.” 为实数积；“+”为a+b=min(1,a+b)下的有界算子。例如：
设
如果取模型Ⅲ，有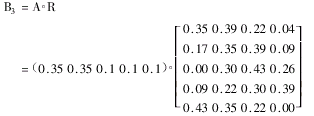
将(ai)1×n各元素与(rij)n×m第j列各元素取小(ai∧rij)后再取
即首先使
, 百拇医药
再在“+”运算下求和
则
同理b3=0.87,b4=0.33。得
用四种广义模糊算子模型分别运算得到：
B1'=(0.30,0.30,0.30,0.10)
B2'=(0.27，0.32，0.32，0.09)
, http://www.100md.com
B3'=(0.24，0.34，0.30，0.11)
B4'=(0.23，0.35，0.31，0.11)
由于选择广义模糊算子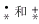的不同，它的结果B也有所不同，可以看到：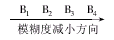
这里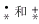是在综合评判中所反映的 鉴别能力。
1.2 多级模糊综合评价模型
, 百拇医药
①一级模糊综合评价
将因素划分为若干个子集合，每个子集合再可以继续划分。那么，每个子集合即为二元模糊 关系矩阵。
H=(hij)n×m
设因素的权数矩阵
A=(ai)1×n
合成运算结果：
②二级模糊综合评价
把前级各子集合进行初始模糊综合评价的结果视为后一级的因素集，得到新的二元模糊关系 矩阵
, 百拇医药
R=(rij)n×m
设因素的权数矩阵
G=(gi)1×n
合成运算结果：
③k级模糊综合评价
2 赔偿医学上的应用
例如：以对某一损伤程度的评价为例，设损伤因素集合为U={机体的完整性破坏、机 体功能障碍、职业劳动能力的丧失、仪表完美性损害、精神心理损害、社会适应能力减少}= {u1、u2、u3、u4、u5、u6}；评价集合V={全部丧失、大部分丧失、部分丧失、小部分丧失、无丧失}={v1、v2、v3、v4、v5}。根据评价资料，用统计方法计算得到二元模糊关系：
, http://www.100md.com
即有50%的专家认为机体的完整性破坏全部丧失，20%的专家认为大部分丧失，10%认为部分 丧失，10%认为小部分丧失，10%认为无丧失；同理类推。求对整个损伤的综合评价程度。
(1)令模糊关系矩阵为：
(2)根据一般经验和医学专家的评定意见，确定各类损伤因素对损伤程度的权数集。
A=(40%、20%、12%、11%、10%、7%)
=(0.40、0.20、0.12、0.11、0.10、0.07)
(3)对该评价对象的模糊综合评价结果为B：
如果取模型Ⅰ，有
, 百拇医药
B=AR
于是
将a(i)1×n各元素与(rij)n×m第j列各元素取小(ai∧r ij)后再在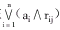
中取大，即首先使
然后将
(ai∧ri2)=(0.40∧0.2,0.20∧0.3,0.12∧0.3,0.11∧0.3,0.1 0∧0.2,0.07∧0.3)
, http://www.100md.com
=(0.20,0.20,0.12,0.11,0.10,0.07)
再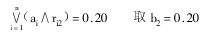
同理可得b3=0.20、b4=0.20、b5=0.10
所以，B=(0.40,0.20,0.20,0.20,0.10)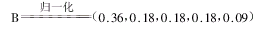
又因为Max(b1，b2，b3，b4，b5)
=Max(0.36,0.18,0.18,0.18,0.09)
, 百拇医药
=0.36
通过运算结果可以看到：该损伤程度的模糊综合评价结果为36%，也就是说，该损伤对某个 体的损害为36%。某个体的精神心理、机体和社会关系总能力减少了36%。因此，模糊综合评 价是主客观的统一，它是一种综合的、抽象的科学评判方法。对不同的损伤，我们都可以根 据这种模糊综合评价的方法来确定各损伤间的程度差别。
作者简介：熊平(1959—)，男，湖南 省湘潭市 人，副教授，法医学硕士生导师，主要从事法医病理学、赔偿医学教学与科研。
参考文献：
[1] 汪培代.模糊集合论及其它应用[M].上海：科技出版社，198 3.
[2] 贺仲雄.模糊数学及其应用[M].天津：科技出版社，1983.
(收稿日期：2000-10-20), http://www.100md.com
单位：熊平(南华大学法医研究与鉴定中心，湖南衡阳 421001)；曾可先(衡阳市公安局刑侦技 术大队，湖南衡阳 421001)
关键词：后遗障碍；查德算子；广义模糊算子；多级模糊综合评判
川北医学院学报000443 摘 要：损伤给受损伤者带来或多或少的后遗障碍，在后遗障碍的评 定中，又受很多因素的影响，特别是这些因素在目前无法进行定量判定。本研究利用模糊综合评判对后遗障碍进行分级分度，以求指导损害赔偿，笔者简述了模糊综合评判模 型的基本概念和原理。同时，通过法医学实例介绍了该模型的应用。
中图分类号：D919 文献标 识码：E
文章编号：1005-3697(2000)04-0055-03
, 百拇医药
Blurred evaluation of injury extent
XIONG Ping ZENG Ke-xian
(Department of Forensic Medicine, South China University, Hengyang,Hu nan, 421001， China)
Abstract:The basic concept and principle of a model of blurre d synthet evaluation was introduced. A blurred syntheticl evaluation of grade a classification for the obstacle of sequelae was used to quide compensation harmn ess. The practice of this model was introduced by forensic medici examples.
, 百拇医药
Key words:blurred operator; blurred syntheticl appraise ev aluation; injury extent
在后遗障碍(残废)评定中，尽管国内外有不少种类的一览表，但每一种表都不能包罗万象。由于损伤的种类很多，再加上多重损伤的排列组 合，使得后遗障碍的类型很多，一览表上无法一一对号入座。在实际工作中往往都是以某地 、某些行政单位制定一览表作为判定的理论基础，由于人们的认识水平和实践经验不同，以 及实际处理结果上的差异，导致所制定的一览表也不尽相同。怎样评定后遗障碍并进行分度 ，我们已作了一些理论分析，对如何区别某一后遗障碍与另一后遗障碍两者的严重程度，特 别是在两种后遗障碍比较接近的情况下，怎样进行分级分度，这是我们一直研究的问题。由 于损伤造成的人身损害是多方面的，它包括生物属性的损害、社会属性的损害、精神心理的 损害、人际关系的损害。而这些方面又由很多因素所构成，所以对一个损伤应采取综合评价 。
, http://www.100md.com
所谓的综合评价就是对某一损伤程度进行全面而恰当的评价。要全面而恰当地评价损伤必须 从如下几个方面考虑：机体的完善性破坏、机体功能障碍、职业劳动能力的丧失、仪表完美 性损害、精神心理损害的程度、社会适应能力减少。又由于每个因素在评价中的“权数”不 尽相同，且评价指标间的关系错综复杂，表现的趋势不完全一致，所以收集到的信息也往往 具有不同程度的模糊性。因此，我们试图用模糊综合评价来进行后遗障碍的分级。
1 基本概念及原理
1.1 广义模糊算子
设：二元模糊关系矩阵
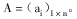权数那么，模糊综合评判是在下的合成运算，其中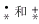为广义模糊算子，常用的模型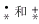有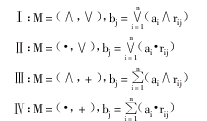：, 百拇医药
其中模型Ⅰ为Zade算子；
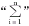为n个数在+运算中求和；“.” 为实数积；“+”为a+b=min(1,a+b)下的有界算子。例如：设
如果取模型Ⅲ，有
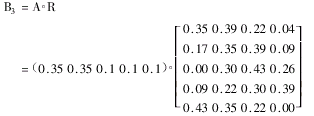
将(ai)1×n各元素与(rij)n×m第j列各元素取小(ai∧rij)后再取
即首先使, 百拇医药
再在“+”运算下求和
则
同理b3=0.87,b4=0.33。得
用四种广义模糊算子模型分别运算得到：
B1'=(0.30,0.30,0.30,0.10)
B2'=(0.27，0.32，0.32，0.09)
, http://www.100md.com
B3'=(0.24，0.34，0.30，0.11)
B4'=(0.23，0.35，0.31，0.11)
由于选择广义模糊算子
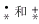的不同，它的结果B也有所不同，可以看到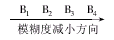：这里
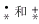是在综合评判中所反映的 鉴别能力。1.2 多级模糊综合评价模型
, 百拇医药
①一级模糊综合评价
将因素划分为若干个子集合，每个子集合再可以继续划分。那么，每个子集合即为二元模糊 关系矩阵。
H=(hij)n×m
设因素的权数矩阵
A=(ai)1×n
合成运算结果：
②二级模糊综合评价
把前级各子集合进行初始模糊综合评价的结果视为后一级的因素集，得到新的二元模糊关系 矩阵
, 百拇医药
R=(rij)n×m
设因素的权数矩阵
G=(gi)1×n
合成运算结果：
③k级模糊综合评价
2 赔偿医学上的应用
例如：以对某一损伤程度的评价为例，设损伤因素集合为U={机体的完整性破坏、机 体功能障碍、职业劳动能力的丧失、仪表完美性损害、精神心理损害、社会适应能力减少}= {u1、u2、u3、u4、u5、u6}；评价集合V={全部丧失、大部分丧失、部分丧失、小部分丧失、无丧失}={v1、v2、v3、v4、v5}。根据评价资料，用统计方法计算得到二元模糊关系：
, http://www.100md.com
即有50%的专家认为机体的完整性破坏全部丧失，20%的专家认为大部分丧失，10%认为部分 丧失，10%认为小部分丧失，10%认为无丧失；同理类推。求对整个损伤的综合评价程度。
(1)令模糊关系矩阵为：
(2)根据一般经验和医学专家的评定意见，确定各类损伤因素对损伤程度的权数集。
A=(40%、20%、12%、11%、10%、7%)
=(0.40、0.20、0.12、0.11、0.10、0.07)
(3)对该评价对象的模糊综合评价结果为B：
如果取模型Ⅰ，有
, 百拇医药
B=AR
于是
将a(i)1×n各元素与(rij)n×m第j列各元素取小(ai∧r ij)后再在
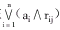中取大，即首先使然后将
(ai∧ri2)=(0.40∧0.2,0.20∧0.3,0.12∧0.3,0.11∧0.3,0.1 0∧0.2,0.07∧0.3)
, http://www.100md.com
=(0.20,0.20,0.12,0.11,0.10,0.07)
再
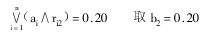
同理可得b3=0.20、b4=0.20、b5=0.10
所以，B=(0.40,0.20,0.20,0.20,0.10)
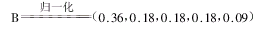
又因为Max(b1，b2，b3，b4，b5)
=Max(0.36,0.18,0.18,0.18,0.09)
, 百拇医药
=0.36
通过运算结果可以看到：该损伤程度的模糊综合评价结果为36%，也就是说，该损伤对某个 体的损害为36%。某个体的精神心理、机体和社会关系总能力减少了36%。因此，模糊综合评 价是主客观的统一，它是一种综合的、抽象的科学评判方法。对不同的损伤，我们都可以根 据这种模糊综合评价的方法来确定各损伤间的程度差别。
作者简介：熊平(1959—)，男，湖南 省湘潭市 人，副教授，法医学硕士生导师，主要从事法医病理学、赔偿医学教学与科研。
参考文献：
[1] 汪培代.模糊集合论及其它应用[M].上海：科技出版社，198 3.
[2] 贺仲雄.模糊数学及其应用[M].天津：科技出版社，1983.
(收稿日期：2000-10-20), http://www.100md.com