描述肺毛细血管中血液氧合过程的反应扩散方程组解的渐近性态
作者：张勤
单位：张勤(南京铁道医学院数学教研室 南京210009)
关键词：肺毛细血管；血液氧合；渐近性态
数理医药学杂志000307
摘 要 描述了肺毛细血管中血液氧合过程的反应扩散方程组解的渐近性态，并给出当Z→+∞时，解趋于稳态解的速度。
中图分类号：O 242.1 文献标识码：A
文章编号：1004-4337(2000)03-0203-03
1 引言
本文考虑如下方程组：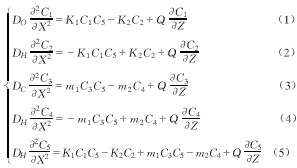
, 百拇医药
这是描述血液在肺毛细血管中氧合过程的方程组[1]，其中C1、C2、C3、C4、C5分别表示O2、HbO2、CO2、HbNHCOOH、Hb在肺毛细血管中的浓度，DO、DC、DH分别表示O2、CO2、Hb的扩散系数，Q表示血流速度，K1、K2、m1、m2是两个可逆化学反应的反应速度，a表示血管半径。
把血管看成对称的，因此
(6)
另外，由于O2、CO2容易透过呼吸膜，可以认为当x=a时，O2、CO2的浓度与肺泡中浓度相等，即
(7)
, 百拇医药
其中Cialv是已知常数。又因为大分子的Hb、HbO2、HbNHCOOH不能透过呼吸膜，因此
(8)
初始条件由静脉血中生理参数确定：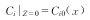
(9)
当Z→+∞时，定解问题(1)～(9)的平衡解为[1]：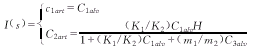
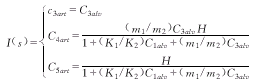
平均解Ciart(i=1,2,3,4,5)分别表示血液流出肺毛细血管进入动脉时，O2、HbO2、CO2、HbNHCOOH、Hb的浓度，其中H是常数，表示单位体积中化学结合的血红蛋白与自由血红蛋白的总量。
, 百拇医药
Wei Feng在文献[2]中讨论了(1)～(9)解的存在性，在文献[3]中讨论了(1)～(5)在边界条件都是Dirichlet条件或都是Robin条件时解的渐近性态，但实际问题不满足这样的边界条件，为了实际应用的需要，本文讨论(1)～(9)的渐近性态。
定理 如果对于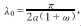
,其中a是血管半径，ω>0常数，存在正常数r1、r2、r3、r4、r5，使得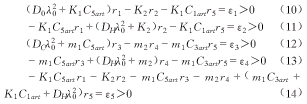
成立，其中Ciart为稳态解(Is)，则存在常数ε*>0，α*>0,只要0<ε<ε*,α>α*，且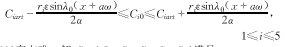
, 百拇医药
(1)～(9)存在唯一解C=(C1,C2,C3,C4,C5)满足
定理说明当初值在稳态解附近时，解也在稳态解附近，且当Z→+∞时，解一致趋于稳态解。
推论 对于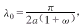
,其中a是血管半径，ω>0,存在正常数K*1、m*1、ε*、α*,只要01*1,01*1,0<ε<ε*,α>α*，初值满足
, http://www.100md.com
(1)～(9)存在唯一解C=(C1,C2,C3,C4,C5)满足
本文定理是对文献[3]的补充，推论是对文献[2]中定理3的部分推广。由本文的结论，可以从理论上证明文献[1]中线性模型是合理的，并且可以把线性模型推广到非线性模型，详细讨论见文献[4]，因此本文结论具有一定的应用价值。
2 定理的证明
定义 对某个常数Z>0，如果两个向量函数
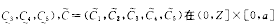上满足下列微分不等式：
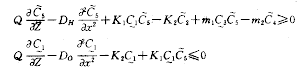
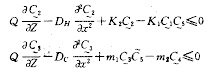
, 百拇医药
在边界上满足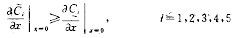
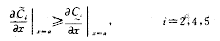
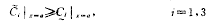
初值满足
则称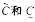
是(1)～(9)的一对上下解。
引理1 若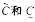是(1)～(9)的一对上下解，则(1)～(9)在(0，Z]×[0,a]上存在唯一解C满足：
, 百拇医药
引理1可以从一般的抛物型方程组的存在比较定理推出。
下面具体构造(1)～(9)的一对上下解。假定定理条件成立，记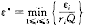
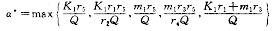作函数
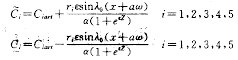
其中ε<ε*,α>α*
可以验证，
与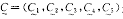
是定解问题(1)～(9)的一对上下解，由引理1，存在唯一解C=(C1,C2,C3,C4,C5)满足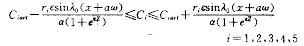
, 百拇医药
引理2 如果对于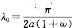
,其中a是血管半径，ω>0是常数，问题(1)～(9)中生理参数满足
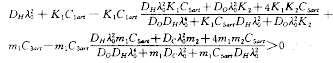(15)
那么存在正常数r1、r2、r3、r4、r5,使式(10)～(14)成立。
证明 只要说明对ε1>0,ε3>0,ε5>0，下列代数方程组有正解。
(DOλ20+K1C5art)r1-K2r2-K1C1artr5=ε1 (10)
, http://www.100md.com
-K1C5artr1+(DHλ20+K2)r2-K1C1artr5=ε1 (11)
(DCλ20+m1C5art)r3-m2r4-m1C3artr5=ε3 (12)
-m1C5artr3+(DHλ20+m2)r4-m1C3artr5=ε3 (13)
, http://www.100md.com
-K1C5artr1-K2r2-m1C5artr3-m2r4+(m1C3art+K1C1art+DHλ20)r5=ε3 (14)
由(10＇),(11＇)得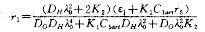
(16)
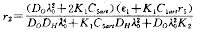(17)
由(12＇),(13＇)得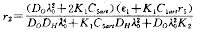 (18)
(19)
, 百拇医药
把式(16)～(19)代入(14＇)得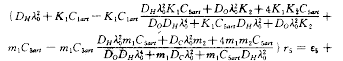
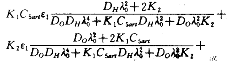
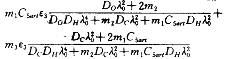
上式右边大于零，由式(15)知r5的系数大于零，故可解得r5>0，把r5代入式(16)～(19)，解得r1、r2、r3、r4都大于零。
引理3 对于
,其中a是血管半径，ω>0，存在K*1>0,m*1>0，使得当01*1,01*1时，存在正常数r1、r2、r3、r4、r5，使式(10)～(14)成立。
, 百拇医药
证明 因为式(15)的左边当K1→0,m1→0时极限为DHλ20>0，所以存在K*1>0,m*1>0，使得当01*1,01*1时(15)式成立，由引理1，存在正常数r1、r2、r3、r4、r5，使式(10)～(14)成立。
参考文献
1，M.P.Singh, K.Khetarpal, and Mathili Sharan, A Theoretical Model for studying the Rate of Oxygenation of Blood in Pulmonary Capillaries, J. Math. Biology 9,305～330.
, 百拇医药
2，Wei Feng, Global. Existence and Boundedness of the Solution for a Blood Oxygenation Model J. Math. Anal. Appl 181, 462～472,1994.
3，Wei Feng, Stability and Asymptotic Behaviour in a keaetion-diffusion System, Mathematical Methocls in the Applied Sciences, Vol 17,155～169, 1994.
4，张勤.肺毛细血管中血液氧合速率的数学模型.数理医药学杂志，1996，9(4)：297～298.
收稿日期：1998-09-29, 百拇医药
单位：张勤(南京铁道医学院数学教研室 南京210009)
关键词：肺毛细血管；血液氧合；渐近性态
数理医药学杂志000307
摘 要 描述了肺毛细血管中血液氧合过程的反应扩散方程组解的渐近性态，并给出当Z→+∞时，解趋于稳态解的速度。
中图分类号：O 242.1 文献标识码：A
文章编号：1004-4337(2000)03-0203-03
1 引言
本文考虑如下方程组：
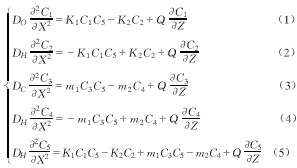
, 百拇医药
这是描述血液在肺毛细血管中氧合过程的方程组[1]，其中C1、C2、C3、C4、C5分别表示O2、HbO2、CO2、HbNHCOOH、Hb在肺毛细血管中的浓度，DO、DC、DH分别表示O2、CO2、Hb的扩散系数，Q表示血流速度，K1、K2、m1、m2是两个可逆化学反应的反应速度，a表示血管半径。
把血管看成对称的，因此
(6)另外，由于O2、CO2容易透过呼吸膜，可以认为当x=a时，O2、CO2的浓度与肺泡中浓度相等，即
(7), 百拇医药
其中Cialv是已知常数。又因为大分子的Hb、HbO2、HbNHCOOH不能透过呼吸膜，因此
(8)初始条件由静脉血中生理参数确定：
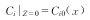(9)当Z→+∞时，定解问题(1)～(9)的平衡解为[1]：
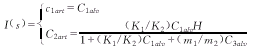
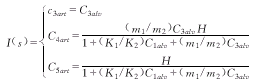
平均解Ciart(i=1,2,3,4,5)分别表示血液流出肺毛细血管进入动脉时，O2、HbO2、CO2、HbNHCOOH、Hb的浓度，其中H是常数，表示单位体积中化学结合的血红蛋白与自由血红蛋白的总量。
, 百拇医药
Wei Feng在文献[2]中讨论了(1)～(9)解的存在性，在文献[3]中讨论了(1)～(5)在边界条件都是Dirichlet条件或都是Robin条件时解的渐近性态，但实际问题不满足这样的边界条件，为了实际应用的需要，本文讨论(1)～(9)的渐近性态。
定理 如果对于
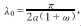,其中a是血管半径，ω>0常数，存在正常数r1、r2、r3、r4、r5，使得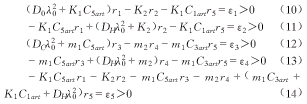成立，其中Ciart为稳态解(Is)，则存在常数ε*>0，α*>0,只要0<ε<ε*,α>α*，且
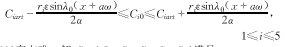
, 百拇医药
(1)～(9)存在唯一解C=(C1,C2,C3,C4,C5)满足
定理说明当初值在稳态解附近时，解也在稳态解附近，且当Z→+∞时，解一致趋于稳态解。
推论 对于
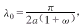,其中a是血管半径，ω>0,存在正常数K*1、m*1、ε*、α*,只要0, http://www.100md.com
(1)～(9)存在唯一解C=(C1,C2,C3,C4,C5)满足
本文定理是对文献[3]的补充，推论是对文献[2]中定理3的部分推广。由本文的结论，可以从理论上证明文献[1]中线性模型是合理的，并且可以把线性模型推广到非线性模型，详细讨论见文献[4]，因此本文结论具有一定的应用价值。
2 定理的证明
定义 对某个常数Z>0，如果两个向量函数
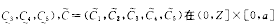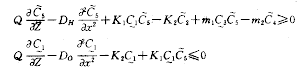
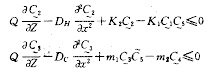
上满足下列微分不等式：, 百拇医药
在边界上满足
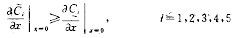
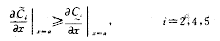
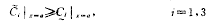
初值满足
则称
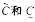是(1)～(9)的一对上下解。引理1 若
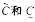是(1)～(9)的一对上下解，则(1)～(9)在(0，Z]×[0,a]上存在唯一解C满足：, 百拇医药
引理1可以从一般的抛物型方程组的存在比较定理推出。
下面具体构造(1)～(9)的一对上下解。假定定理条件成立，记
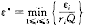
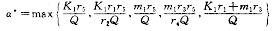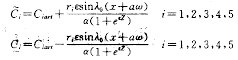
作函数其中ε<ε*,α>α*
可以验证，
与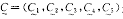是定解问题(1)～(9)的一对上下解，由引理1，存在唯一解C=(C1,C2,C3,C4,C5)满足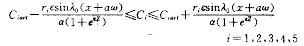, 百拇医药
引理2 如果对于
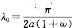,其中a是血管半径，ω>0是常数，问题(1)～(9)中生理参数满足 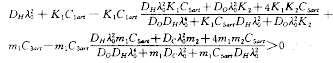(15)那么存在正常数r1、r2、r3、r4、r5,使式(10)～(14)成立。
证明 只要说明对ε1>0,ε3>0,ε5>0，下列代数方程组有正解。
(DOλ20+K1C5art)r1-K2r2-K1C1artr5=ε1 (10)
, http://www.100md.com
-K1C5artr1+(DHλ20+K2)r2-K1C1artr5=ε1 (11)
(DCλ20+m1C5art)r3-m2r4-m1C3artr5=ε3 (12)
-m1C5artr3+(DHλ20+m2)r4-m1C3artr5=ε3 (13)
, http://www.100md.com
-K1C5artr1-K2r2-m1C5artr3-m2r4+(m1C3art+K1C1art+DHλ20)r5=ε3 (14)
由(10＇),(11＇)得
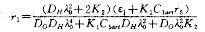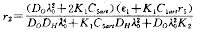(16) (17)由(12＇),(13＇)得
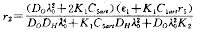(18) (19), 百拇医药
把式(16)～(19)代入(14＇)得
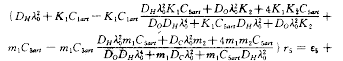
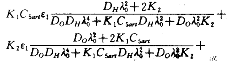
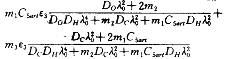
上式右边大于零，由式(15)知r5的系数大于零，故可解得r5>0，把r5代入式(16)～(19)，解得r1、r2、r3、r4都大于零。
引理3 对于
,其中a是血管半径，ω>0，存在K*1>0,m*1>0，使得当0, 百拇医药
证明 因为式(15)的左边当K1→0,m1→0时极限为DHλ20>0，所以存在K*1>0,m*1>0，使得当0
参考文献
1，M.P.Singh, K.Khetarpal, and Mathili Sharan, A Theoretical Model for studying the Rate of Oxygenation of Blood in Pulmonary Capillaries, J. Math. Biology 9,305～330.
, 百拇医药
2，Wei Feng, Global. Existence and Boundedness of the Solution for a Blood Oxygenation Model J. Math. Anal. Appl 181, 462～472,1994.
3，Wei Feng, Stability and Asymptotic Behaviour in a keaetion-diffusion System, Mathematical Methocls in the Applied Sciences, Vol 17,155～169, 1994.
4，张勤.肺毛细血管中血液氧合速率的数学模型.数理医药学杂志，1996，9(4)：297～298.
收稿日期：1998-09-29, 百拇医药