部分性脾动脉栓塞治疗特发性血小板减少性紫癜
作者:汪世存 孙 冰 孙一兵 李国琪 黄胜友 齐志刚
单位:安徽省立医院放射科, 安徽 合肥 230001
关键词:紫癜;血小板减少;脾动脉栓塞;治疗
疾病控制杂志990344 【文献标识码】 A
【中图分类号】 O211.67; R183
【文章编号】 1008-6013(1999)03-0235-01
The application of the model of GM(1,1) in predicting infectious diseases
QI Xian-ying
, http://www.100md.com
本文根据灰色系统理论,利用某高校9年来3种主要传染病的逐年发病率的统计资料,运用GM(1,1)灰色预测模型方法,对某高等学校传染病的发病率趋势进行动态预测。
1 建模的方法步骤
1.1 给定原始时间序列,并记作
x(0)=(x(0)(1),x(0)(2),…x(0)(N));
1.2 对于数列作一次累加生成AGO
x(1)=(x(1)(1),x(1)(2),…x(1)(N)),式中
, http://www.100md.com
1.3 构造累加矩阵B与常数项向量YN
YN=(x(0)(2),x(0)(3),…,x(0)(N))T,建立相应的微分方程模型为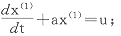
1.4 用最小二乘法求解灰参数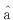
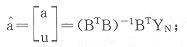
u=(BTB)-1BTYN;
, http://www.100md.com
1.5 该模型的时间响应函数为
1.6 对x(1)求导还原得到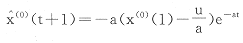
1.7 计算x(0)(t)与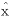 (0)(t)之差及相对误差
(0)(t)之差及相对误差
e(1)(t)=x(0)(t)-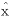 (0)(t),q(t)=e(0)(t)/x(0)(t);
(0)(t),q(t)=e(0)(t)/x(0)(t);
, http://www.100md.com
1.8 利用上述模型进行预测。
3 应用实例
本文应用实例采用的数据为某高校9年来3种主要传染病的逐年发病率的资料(表1)。
表1 某高校9年来3种主要传染病的逐年发病率(1/万) 年度
1989
1990
1991
1992
1993
1994
1995
, 百拇医药
1996
1997
传染病
100.53
85.62
64.53
86.63
105.89
83.55
116.47
135.93
56.56
痢 疾
, 百拇医药
19.46
44.19
30.98
45.86
55.47
60.34
71.90
94.93
38.38
肝 炎
9.73
8.29
25.81
, 百拇医药
38.22
25.21
18.57
33.43
36.68
14.14
疟 疾
71.34
33.14
7.74
2.55
25.21
4.64
, 百拇医药
11.14
4.32
4.04
根据建模方法,利用表1资料及GM(1,1)程序,经过微机计算,分别建立发病率趋势GM(1,1)灰色预测模型:
以上四种模型的关联度分别为0.875、0.875、1、1,模拟预测效果较好。根据以上四种GM(1,1)预测模型,预测结果见表2。表2 某高校1998~2002年传染病发病率的预测值(1/万) 年 度
1998
1999
2000
, 百拇医药
2001
2002
传染病
106.46
112.07
118.12
124.81
132.05
痢 疾
74.90
80.30
86.09
92.30
, 百拇医药
98.95
肝 炎
28.50
29.34
30.20
31.09
32.00
疟 疾
3.06
2.37
1.83
1.42
1.10
通过表2可以看出:高校传染病发病率总体上呈上升趋势。痢疾和肝炎均呈递增趋势。因此,痢疾和肝炎的防治应成为高校医疗卫生工作的重点。疟疾的发病率呈下降趋势,这与当前高校环境卫生、寝室卫生条件的改善有很大关系。
【作者简介】 齐显影(1968-),女,护师
(收稿日期 1999-01-28), http://www.100md.com
单位:安徽省立医院放射科, 安徽 合肥 230001
关键词:紫癜;血小板减少;脾动脉栓塞;治疗
疾病控制杂志990344 【文献标识码】 A
【中图分类号】 O211.67; R183
【文章编号】 1008-6013(1999)03-0235-01
The application of the model of GM(1,1) in predicting infectious diseases
QI Xian-ying
, http://www.100md.com
本文根据灰色系统理论,利用某高校9年来3种主要传染病的逐年发病率的统计资料,运用GM(1,1)灰色预测模型方法,对某高等学校传染病的发病率趋势进行动态预测。
1 建模的方法步骤
1.1 给定原始时间序列,并记作
x(0)=(x(0)(1),x(0)(2),…x(0)(N));
1.2 对于数列作一次累加生成AGO
x(1)=(x(1)(1),x(1)(2),…x(1)(N)),式中

, http://www.100md.com
1.3 构造累加矩阵B与常数项向量YN

YN=(x(0)(2),x(0)(3),…,x(0)(N))T,建立相应的微分方程模型为
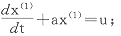
1.4 用最小二乘法求解灰参数
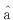
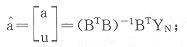
u=(BTB)-1BTYN;
, http://www.100md.com
1.5 该模型的时间响应函数为

1.6 对x(1)求导还原得到
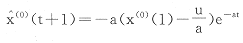
1.7 计算x(0)(t)与
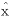 (0)(t)之差及相对误差
(0)(t)之差及相对误差e(1)(t)=x(0)(t)-
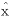 (0)(t),q(t)=e(0)(t)/x(0)(t);
(0)(t),q(t)=e(0)(t)/x(0)(t);, http://www.100md.com
1.8 利用上述模型进行预测。
3 应用实例
本文应用实例采用的数据为某高校9年来3种主要传染病的逐年发病率的资料(表1)。
表1 某高校9年来3种主要传染病的逐年发病率(1/万) 年度
1989
1990
1991
1992
1993
1994
1995
, 百拇医药
1996
1997
传染病
100.53
85.62
64.53
86.63
105.89
83.55
116.47
135.93
56.56
痢 疾
, 百拇医药
19.46
44.19
30.98
45.86
55.47
60.34
71.90
94.93
38.38
肝 炎
9.73
8.29
25.81
, 百拇医药
38.22
25.21
18.57
33.43
36.68
14.14
疟 疾
71.34
33.14
7.74
2.55
25.21
4.64
, 百拇医药
11.14
4.32
4.04
根据建模方法,利用表1资料及GM(1,1)程序,经过微机计算,分别建立发病率趋势GM(1,1)灰色预测模型:

以上四种模型的关联度分别为0.875、0.875、1、1,模拟预测效果较好。根据以上四种GM(1,1)预测模型,预测结果见表2。表2 某高校1998~2002年传染病发病率的预测值(1/万) 年 度
1998
1999
2000
, 百拇医药
2001
2002
传染病
106.46
112.07
118.12
124.81
132.05
痢 疾
74.90
80.30
86.09
92.30
, 百拇医药
98.95
肝 炎
28.50
29.34
30.20
31.09
32.00
疟 疾
3.06
2.37
1.83
1.42
1.10
通过表2可以看出:高校传染病发病率总体上呈上升趋势。痢疾和肝炎均呈递增趋势。因此,痢疾和肝炎的防治应成为高校医疗卫生工作的重点。疟疾的发病率呈下降趋势,这与当前高校环境卫生、寝室卫生条件的改善有很大关系。
【作者简介】 齐显影(1968-),女,护师
(收稿日期 1999-01-28), http://www.100md.com