应用Poisson分布与负二项分布探讨麻风病例空间聚集性
http://www.100md.com
37c医学网
作者：王成科
单位：王成科(四川省蓬溪县卫生防疫站 蓬溪629100)
关键词：
数理医药学杂志000521 中图分类号： R 755.01 文献标识码： B 文章编号：1004-4337(2000)05-0422-01
蓬溪县位于川中浅丘，总人口127万。有麻风病例68例，分布于全县38个乡、48个行政自然村，以村为单位的疫源性指数为1.42，这种高度分散病例的传染关系很难查清，其空间分布形式是否改变了传染性疾病聚集性分布的特点?本文就68例麻风病例以村为单位的空间分布试作负二项分布和Poisson分布拟合，并作拟合优度χ2检验，为防治工作提供了科学依据。
1 材料与方法
, 百拇医药
以该县历年确诊的麻风病例为依据，以行政自然村为单位，按发病例数分类统计，无病例的村为零频数分布，全县共862个自然村，其中有病例的48个，68例。
根据资料，分别进行Poisson分布和负二项分布拟合，并作拟合优度χ2检验。
1.1 Poisson分布模型[1]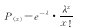
(1)
NP(x)=N*P(x) (2)
上述P(x)亦可用下式作递推计算：
P(0)=e-λ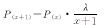
(3)
, 百拇医药
式中，P(x)为出现计数为x的概率；NP(x)为理论频数；N为样本总数；e为自然对数的底，e=2.71828；λ为平均数；x为以村为单位的病例数；x=0,1,2,……；x!为x的阶乘，0!=1。
1.2 负二项分布模型[1]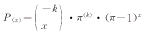
(4)
NP(x)=N*P(x) (5)
上述P(x)的递推公式为：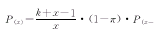
(6)
式中，k>0,0<π<1,x=0,1,2……；P(x)、N、x的含义同前；π为常数；k是表示聚集程度的参数，两者由矩法求之[1]。
, 百拇医药
2 结果与分析
Poisson分布概率模型与负二项分布概率模型拟合及优度χ2检验见表1。结果不符合Poisson分布(P<0.01)，而与负二项分布非常满意的配合(P>0.20)。
Poisson分布是一种离散型随机变量分布概型，当母体很大，而概率很小(P≤0.01)时的分布概型是负二项分布的一种极限形式，它的特征是每个发生个体的存在绝不影响其它个体的分布。负二项分布则是一种非随机性的聚集性分布概型，它的特征是真正的核心聚集，即每个单位内阳性个体的存在可能影响其它个体出现的阳性概率。k值是表示这种聚集程度的参数，k值越小，聚集性越大，其随机的可能性就越小。反之，k值越大，其聚集性越小，随机的可能性就越大，当k→∞时，则为Poisson分布。
表1 麻风病例空间分布实际频数与两种理论
频数分布χ2优度检验 村内病
, 百拇医药
例数
实际
频数
负二项分布
Poisson分布
理论频数
χ2
理论频数
χ2
0
814
813.5400
0.0003
, 百拇医药
796.6021
0.3800
1
36
35.5502
0.0057
62.8519
11.4719
2
3
4
6
4
, 百拇医药
2
8.7027
2.7138
1.4933
0.8393
0.7641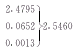
35.1053
χ2
1.6094
46.9571
df
, 百拇医药
4-3=1
3-2=1
P
>0.20
<0.001
注：
=0.0789,S2=0.1424,K=0.0980
通过对该县麻风病例实际空间分布频数与Poisson分布和负二项分布配合，表明该县麻风病例以村为单位的实际空间分布符合聚集性的负二项分布(P>0.20)，而且实际分布的信息也具有负二项分布的方差(S2=0.1424)>平均数(=0.0789)的特点[2]。本文中聚集性参数k=0.0980，显示了较强的聚集性。证实了麻风这种慢性传染病在病灶内仍具有传染性疾病聚集性分布的特征。表明病例的发生与分布仍然与麻风病的流行因素、传染源、当地居民的免疫水平等因素有关。这些因素直接和间接影响着病例在一定空间的聚集程度。因此，麻风病例的空间分布仍具有传染性疾病聚集性特征时，防治措施只能加强，而不能削弱，其工作重点应放在麻风病的普查，同时应加强监测工作。 参 考 文 献
1，郭祖超主编.医用数理统计方法.第三版.北京：人民卫生出版社，1988，149～168.
2，刘延龄等.几种离散分布的判定问题.中国卫生统计，1989，(6)5：14.
收稿日期：2000-04-11, 百拇医药
单位：王成科(四川省蓬溪县卫生防疫站 蓬溪629100)
关键词：
数理医药学杂志000521 中图分类号： R 755.01 文献标识码： B 文章编号：1004-4337(2000)05-0422-01
蓬溪县位于川中浅丘，总人口127万。有麻风病例68例，分布于全县38个乡、48个行政自然村，以村为单位的疫源性指数为1.42，这种高度分散病例的传染关系很难查清，其空间分布形式是否改变了传染性疾病聚集性分布的特点?本文就68例麻风病例以村为单位的空间分布试作负二项分布和Poisson分布拟合，并作拟合优度χ2检验，为防治工作提供了科学依据。
1 材料与方法
, 百拇医药
以该县历年确诊的麻风病例为依据，以行政自然村为单位，按发病例数分类统计，无病例的村为零频数分布，全县共862个自然村，其中有病例的48个，68例。
根据资料，分别进行Poisson分布和负二项分布拟合，并作拟合优度χ2检验。
1.1 Poisson分布模型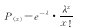[1]
(1)NP(x)=N*P(x) (2)
上述P(x)亦可用下式作递推计算：
P(0)=e-λ
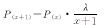(3), 百拇医药
式中，P(x)为出现计数为x的概率；NP(x)为理论频数；N为样本总数；e为自然对数的底，e=2.71828；λ为平均数；x为以村为单位的病例数；x=0,1,2,……；x!为x的阶乘，0!=1。
1.2 负二项分布模型[1]
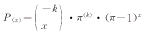(4)NP(x)=N*P(x) (5)
上述P(x)的递推公式为：
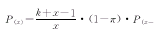(6)式中，k>0,0<π<1,x=0,1,2……；P(x)、N、x的含义同前；π为常数；k是表示聚集程度的参数，两者由矩法求之[1]。
, 百拇医药
2 结果与分析
Poisson分布概率模型与负二项分布概率模型拟合及优度χ2检验见表1。结果不符合Poisson分布(P<0.01)，而与负二项分布非常满意的配合(P>0.20)。
Poisson分布是一种离散型随机变量分布概型，当母体很大，而概率很小(P≤0.01)时的分布概型是负二项分布的一种极限形式，它的特征是每个发生个体的存在绝不影响其它个体的分布。负二项分布则是一种非随机性的聚集性分布概型，它的特征是真正的核心聚集，即每个单位内阳性个体的存在可能影响其它个体出现的阳性概率。k值是表示这种聚集程度的参数，k值越小，聚集性越大，其随机的可能性就越小。反之，k值越大，其聚集性越小，随机的可能性就越大，当k→∞时，则为Poisson分布。
表1 麻风病例空间分布实际频数与两种理论
频数分布χ2优度检验 村内病
, 百拇医药
例数
实际
频数
负二项分布
Poisson分布
理论频数
χ2
理论频数
χ2
0
814
813.5400
0.0003
, 百拇医药
796.6021
0.3800
1
36
35.5502
0.0057
62.8519
11.4719
2
3
4
6
4
, 百拇医药
2
8.7027
2.7138
1.4933
0.8393
0.7641
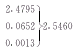
35.1053
χ2
1.6094
46.9571
df
, 百拇医药
4-3=1
3-2=1
P
>0.20
<0.001
注：
=0.0789,S2=0.1424,K=0.0980通过对该县麻风病例实际空间分布频数与Poisson分布和负二项分布配合，表明该县麻风病例以村为单位的实际空间分布符合聚集性的负二项分布(P>0.20)，而且实际分布的信息也具有负二项分布的方差(S2=0.1424)>平均数(
=0.0789)的特点[2]。本文中聚集性参数k=0.0980，显示了较强的聚集性。证实了麻风这种慢性传染病在病灶内仍具有传染性疾病聚集性分布的特征。表明病例的发生与分布仍然与麻风病的流行因素、传染源、当地居民的免疫水平等因素有关。这些因素直接和间接影响着病例在一定空间的聚集程度。因此，麻风病例的空间分布仍具有传染性疾病聚集性特征时，防治措施只能加强，而不能削弱，其工作重点应放在麻风病的普查，同时应加强监测工作。 参 考 文 献1，郭祖超主编.医用数理统计方法.第三版.北京：人民卫生出版社，1988，149～168.
2，刘延龄等.几种离散分布的判定问题.中国卫生统计，1989，(6)5：14.
收稿日期：2000-04-11, 百拇医药