概率论数理统计与随机过程.pdf
http://www.100md.com
2020年11月18日
 |
| 第1页 |
 |
| 第7页 |
 |
| 第17页 |
 |
| 第21页 |
 |
| 第35页 |
 |
| 第525页 |
参见附件(29489KB,675页)。
包含了概率论的基本概念、随机变量及其概率分布、多元随机变量及其分布、随机变量的数字特征、统计量与抽样分布、参数估计、假设检验、随机过程基本概念等的一本非常不错的学习书籍,作者张帼奋,由浙江大学出版社出版。

概率论数理统计与随机过程图片预览
目录大全
第一章概率论的基本概念
1.1样本空间、随机事件
1.2频率与概率
1.3等可能概型
1.4条件概率
1.5事件的独立性与独立试验
思考题一
习题一
第二章随机变量及其概率分布
2.1随机变量
2.2离散型随机变量
2.3随机变量的概率分布函数
2.4连续型随机变量
2.5随机变量函数的分布
思考题二
习题二
第三章多元随机变量及其分布
3.1二元离散型随机变量
3.2二元随机变量的分布函数
3.3二元连续型随机变量
3.4随机变量的独立性
3.5二元随机变量函数的分布
思考题三
习题三
第四章随机变量的数字特征
4.1数学期望
4.2方差、变异系数
4.3协方差与相关系数
4.4其他数字特征
4.5多元随机变量的数字特征
思考题四
习题四
第五章大数定律及中心极限定理
5.1大数定律
5.2中心极限定理
思考题五
习题五
第六章统计量与抽样分布
6.1随机样本与统计量
6.2X6分布t分布F分布
6.3正态总体下的抽样分布
6.4附录
思考题六
习题六
第七章参数估计
7.1点估计
7.2估计量的评价准则
7.3区间估计
7.4正态总体参数的区间估计
7.5非正态总体参数的区间估计
思考题七
习题七
第八章假设检验
8.1假设检验的基本思想
8.2单个正态总体参数的假设检验
8.3两个正态总体参数的假设检验
8.4假设检验与区间估计
8.5拟合优度检验
思考题八
习题八
第九章方差分析与回归分析
9.1单因素方差分析
9.2多因素方差分析
9.3相关系数
9.4一元线性回归
9.5多元回归分析
9.6回归诊断
9.7附录
思考题九
习题九
第十章随机过程基本概念
10.1定义和例子
10.2有限维分布
10.3均值函数和协方差函数
思考题十
习题十
第十一章马尔可夫链
11.1马尔可夫链的定义
11.2有限维分布
11.3常返和暂留
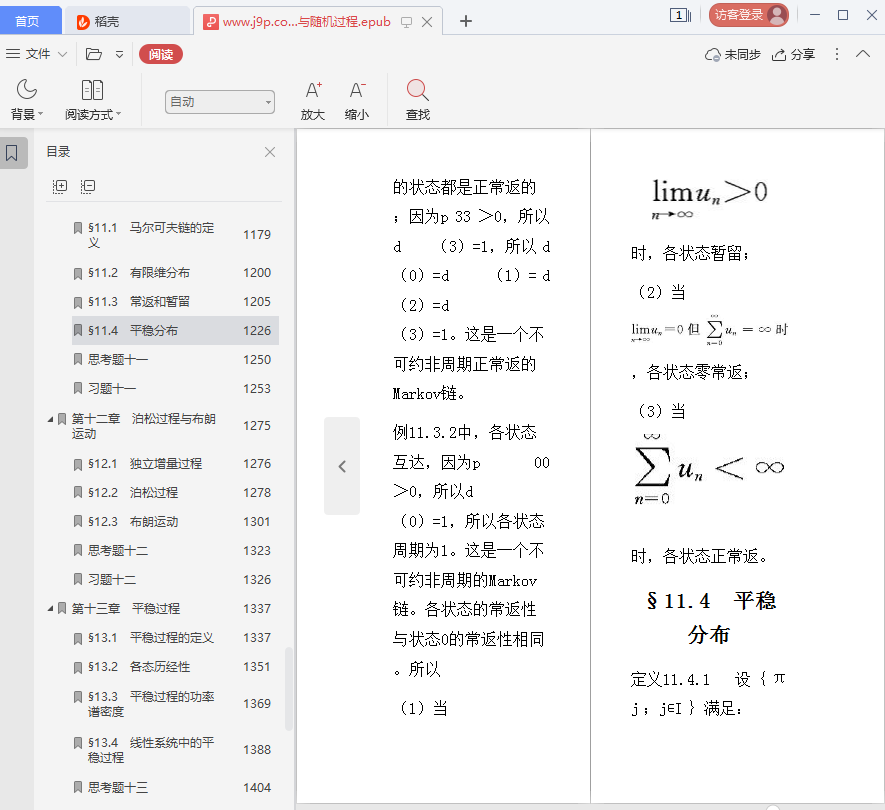
11.4平稳分布
思考题十一
习题十一
第十二章泊松过程与布朗运动
12.1独立增量过程
12.2泊松过程
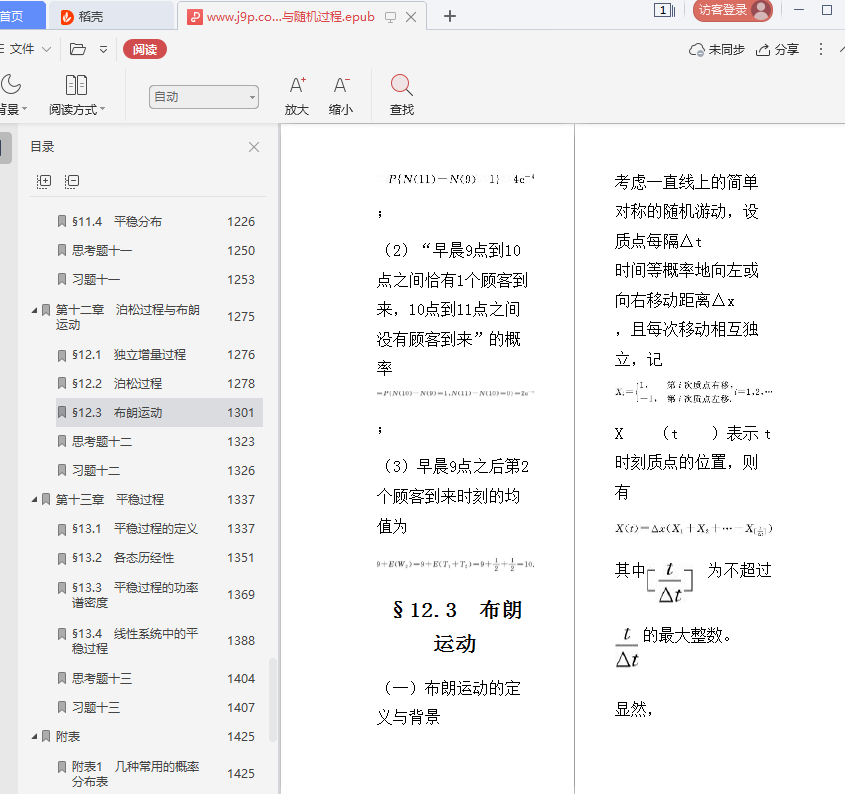
12.3布朗运动
思考题十二
习题十二
第十三章平稳过程
13.1平稳过程的定义
13.2各态历经性
13.3平稳过程的功率谱密度
13.4线性系统中的平稳过程
思考题十三
习题十三
附表
附表1几种常用的概率分布表
附表2标准正态分布表
附表3t分布表
附表4X6分布表
附表5F分布表
附表6柯尔莫哥洛夫检验临界值Dn,á
附表7柯尔莫哥洛夫检验统计量Dn的极限分布
附表8W检验统计量W的系统醝(n)的值
附表9W检验统计量W的岱治皇齏á
附表10D检验统计量Y的岱治皇齓á
思考题、习题参考答案
参考文献
内容简介
《概率论、数理统计与随机过程》介绍概率论的基本知识,阐述了统计量与抽样分布,参数估计,假设检验,方差分析与回归分析,以及随机过程的基本知识。《概率论、数理统计与随机过程》是为非统计专业本科生编写的教科书,也可以作为有微积分基础的科研工作者学习与使用概率论,数理统计与随机过程的基本概念与方法的参考材料。
前言阅读
本书是为非统计专业本科生编写的教科书,也可以作为有微积分基础的科研工作者学习与使用概率论,数理统计与随机过程的基本概念与方法的参考材料。
本书分为三部分:第一部分(第一章至第五章)是概率论部分,主要介绍概率论的基本知识,包括一元,二元离散型随机变量和连续型随机变量的分布,数字特征等;第二部分(第六章至第九章)是数理统计部分,介绍了统计量与抽样分布,参数估计,假设检验,方差分析与回归分析;第三部分(第十章至第十三章)介绍随机过程的基本知识,马尔可夫链,泊松过程,布朗运动和平稳过程。各部分的教学时数都约为24学时,概率论部分的教学时数可以稍多些。数理统计与随机过程的内容是独立的,可以根据需要开设概率论与数理统计或概率论与随机过程课程。
内容摘选
多元随机变量及其分布
在第二章中,我们研究了单个随机变量的概率分布问题,但许多随机现象用一个变量来描述是不够的,例如要预报明天的天气状况,就要观察与预测许多个随机变量(如:温度、湿度、风力,等等)的变化情况,又比如要制定一地区成年男子衬衣(大、中、小号的尺寸)标准,就需要研究这些人的衣长、袖长、领围、肩宽、胸围,等等随机变量以及这些量之间的关系。所以研究多元随机变量是必需的。本教材将较深入地研究二元随机变量,可能时可以将这些方法用于研究多元随机变量。
设一随机试验E ,其样本空间为S ={e ),定义随机变量X=X(e),Y=Y(e) ,称向量(X,Y )为二元随机向量 或称二元随机变量 。
概率论数理统计与随机过程版截图
概率论、数理统计与随机过程
主 编 张帼奋
副主编 黄柏琴 张彩伢《概率论、数理统计与随机过程》
编委会
主 编 张帼奋
副主编 黄柏琴 张彩伢
编 委 张 奕 赵敏智 黄 炜图书在版编目(CIP)数据
概率论、数理统计与随机过程张帼奋主编.—杭州:浙江大学出版
社,2011.7
ISBN 978-7-308-08852-7
Ⅰ.①概… Ⅱ.①张… Ⅲ.①概率论-高等学校-教材②数理统计
-高等学校-教材③随机过程-高等学校-教材 Ⅳ.①021
中国版本图书馆CIP数据核字(2011)第134518号
概率论、数理统计与随机过程
主 编 张帼奋
副主编 黄柏琴 张彩伢
责任编辑 余健波
封面设计 续设计
出版发行 浙江大学出版社
(杭州天目山路148号 邮政编码310007)
(网址:http:www.zjupress.com)
排 版 杭州中大图文设计有限公司
印 刷 德清县第二印刷厂
开 本 787mm×1092mm 116
印 张 18.25
字 数 558千版 印 次 2011年7月第1版 2011年7月第1次印刷
书 号 ISBN 978-7-308-08852-7
定 价 32.00元
版权所有 翻印必究 印装差错 负责调换
浙江大学出版社发行部邮购电话 (0571)88925591前言
本书是为非统计专业本科生编写的教科书,也可以作为有微积分基
础的科研工作者学习与使用概率论,数理统计与随机过程的基本概念与
方法的参考材料。
本书分为三部分:第一部分(第一章至第五章)是概率论部分,主
要介绍概率论的基本知识,包括一元,二元离散型随机变量和连续型随
机变量的分布,数字特征等;第二部分(第六章至第九章)是数理统计
部分,介绍了统计量与抽样分布,参数估计,假设检验,方差分析与回
归分析;第三部分(第十章至第十三章)介绍随机过程的基本知识,马
尔可夫链,泊松过程,布朗运动和平稳过程。各部分的教学时数都约为
24学时,概率论部分的教学时数可以稍多些。数理统计与随机过程的内
容是独立的,可以根据需要开设概率论与数理统计或概率论与随机过程
课程。
本书的主要特点有:(1)在每章的习题前列出了思考题,使读者
对每章的内容有更清晰的梳理;(2)在某些章节尤其是数理统计部分
的例子后介绍了Excel软件应用,使读者不仅掌握概率统计的原理,还
能对大量复杂的数据运用软件进行直接分析;(3)例题和习题的选取
上尽可能贴近生活,兼顾趣味性,有实际意义。
本书的第一章到第三章由黄柏琴编写;第四,第五章由黄炜编写;
第六,第九章由张奕编写;第七,第八章由张彩伢编写;第十,第十一
章由赵敏智编写;第十二,第十三章由张帼奋编写,最后的统稿由张帼
奋完成。编者中除了张彩伢是浙江大学城市学院教师,其余都是浙江大
学教师。书中的部分介绍,例题和习题参考了书后所列的书目,在此特
向有关的作者和出版社表示衷心的感谢。
参加本书编写的教师都长期从事教学科研工作,有丰富的教学实践
经验,书中的不少内容是我们教学科研工作的总结,愿与广大读者交流
分享。
张立新教授对本书的讲义进行了审阅,并提出了宝贵的意见,在此
也向他表示由衷的谢意。另外还要感谢其他对本教材的讲义提出意见和
给予帮助的老师和研究生等。在写作过程中我们努力做到内容由浅入深,所选例题典型新颖,解
题过程条理清晰.由于编者水平有限,书中可能还有不少的缺陷,恳请
各位同行,专家和广大的读者朋友批评指正。
本书编委会
2011年5月目录
前言
第一章 概率论的基本概念
§1.1 样本空间、随机事件
§1.2 频率与概率
§1.3 等可能概型
§1.4 条件概率
§1.5 事件的独立性与独立试验
思考题一
习题一
第二章 随机变量及其概率分布
§2.1 随机变量
§2.2 离散型随机变量
§2.3 随机变量的概率分布函数
§2.4 连续型随机变量
§2.5 随机变量函数的分布
思考题二
习题二
第三章 多元随机变量及其分布
§3.1 二元离散型随机变量
§3.2 二元随机变量的分布函数
§3.3 二元连续型随机变量
§3.4 随机变量的独立性
§3.5 二元随机变量函数的分布
思考题三
习题三
第四章 随机变量的数字特征
§4.1 数学期望
§4.2 方差、变异系数
§4.3 协方差与相关系数
§4.4 其他数字特征
§4.5 多元随机变量的数字特征
思考题四
习题四
第五章 大数定律及中心极限定理§5.1 大数定律
§5.2 中心极限定理
思考题五
习题五
第六章 统计量与抽样分布
§6.1 随机样本与统计量
§6.2 x2分布,t分布,F分布
§6.3 正态总体下的抽样分布
§6.4 附录
思考题六
习题六
第七章 参数估计
§7.1 点估计
§7.2 估计量的评价准则
§7.3 区间估计
§7.4 正态总体参数的区间估计
§7.5 非正态总体参数的区间估计
思考题七
习题七
第八章 假设检验
§8.1 假设检验的基本思想
§8.2 单个正态总体参数的假设检验
§8.3 两个正态总体参数的假设检验
§8.4 假设检验与区间估计
§8.5 拟合优度检验
思考题八
习题八
第九章 方差分析与回归分析
§9.1 单因素方差分析
§9.2 多因素方差分析
§9.3 相关系数
§9.4 一元线性回归
§9.5 多元回归分析
§9.6 回归诊断
§9.7 附录
思考题九
习题九第十章 随机过程基本概念
§10.1 定义和例子
§10.2 有限维分布
§10.3 均值函数和协方差函数
思考题十
习题十
第十一章 马尔可夫链
§11.1 马尔可夫链的定义
§11.2 有限维分布
§11.3 常返和暂留
§11.4 平稳分布
思考题十一
习题十一
第十二章 泊松过程与布朗运动
§12.1 独立增量过程
§12.2 泊松过程
§12.3 布朗运动
思考题十二
习题十二
第十三章 平稳过程
§13.1 平稳过程的定义
§13.2 各态历经性
§13.3 平稳过程的功率谱密度
§13.4 线性系统中的平稳过程
思考题十三
习题十三
附表
附表1 几种常用的概率分布表
附表2 标准正态分布表
附表3 t分布表
附表4 x2分布表
附表5 F分布表
附表6 柯尔莫哥洛夫检验临界值Dn,α
附表7 柯尔莫洛未检鸟金统计量Dn的极限分布
附表8 W检验统计量W的系统αi(n)的值
附表9 W检验统计量W的α分位数Wα
附表10 D检验统计量Y的α分位数Yα思考题、习题参考答案
参考文献第一章 概率论的基本概念
自然界的现象可以分为两大类:一类为必然现象,另一类为随机现
象。
所谓必然现象,是指在一定的条件下必然发生的现象。例如:在一
个标准大气压下,水加热到100℃一定会沸腾;向上抛一重物,一定会
落到地面上;月亮一定沿某一轨道绕地球运转,等等。研究这些必然现
象中的数量关系,常常采用微积分、代数、几何及其他一些数学方法。
所谓随机现象,也称为偶然现象,是指在一定条件下具有多种可能
发生的结果,而对于究竟发生哪一个结果事先不能肯定的现象。例
如:“明天天气”可能是晴,也可能是阴或雨;从一批产品中任意抽取一
件产品,该产品可能是合格品,也可能是不合格品;同一工人在同一台
车床上用同样的材料加工同类型的轴,其直径也不会完全相同;某一时
刻某柜台的顾客数可能为0,1,2,3,…,等等,这些仅仅是“瞬息万
变”的大千世界中的一点点事实。从表面上看,随机现象完全由偶然性
在起支配作用,没有什么必然性。其实,这些现象有一个共同的特点:
在一定的条件下,当我们重复观察随机现象的时候,就会发现随机现象
的出现有其规律性。例如:从一大批产品中,每抽一件产品,该产品是
合格或是不合格是随机的,这是现象具有偶然性的一面;然而,当重复
抽取产品时,不合格品率是稳定的,这就是现象具有的必然性的一面。
再如,当一辆汽车按正常操作通过某一地段时,事先无法确切知道会不
会发生交通事故,即带有偶然性;但经过大量的观察,发现某一地段发
生交通事故比较多,因此就在这一地段的路边立了一块“事故多发地
段”的牌子(这就是必然的一面,即有规律性的一面),提醒人们引起
注意。由此可见,随机现象的出现是偶然的,但在大量重复试验(观
察)中,随机现象隐藏着必然的规律性,这种固有的规律性称为统计规
律性。概率论、数理统计与随机过程就是研究随机现象数量规律性的学
科。§1.1 样本空间、随机事件
(一)样本空间、随机事件
为了精细地考察一个随机现象,必须分析这个随机现象的各种结
果,只有弄清了一个随机现象的各种结果,才能进一步研究这个随机现
象的各种结果出现的可能性。对随机现象作一次观察(或记录、或试
验)称为随机试验(random experiment),这些试验具有以下特点:
(1)可以在相同的条件下重复进行;
(2)每次试验可能出现的结果不止一个,但能事先明确试验的所
有可能结果;
(3)试验完成前不能确定哪个结果会出现。
本书中以后提到的试验都是指随机试验。
称随机试验的所有可能结果构成的集合为样本空间(sample
space),记为S.样本空间S中的每一个元素,即试验的每一个结果称
为样本点(sample point)。
观察随机现象时,人们常常关心某些特定的结果,这些结果可能出
现,也可能不出现。在随机试验中,称那些可能发生又可能不发生的结
果为随机事件(random event),简称事件。特别地,称试验的每一个
结果(即样本点)为基本事件。
我们常用集合的方法描述样本空间及随机事件,那么随机事件即为
样本空间的一个子集。
例1.1.1 投掷一枚硬币,试验的结果有2个:“正面朝上”,“反面朝
上”,故该试验所对应的样本空间由上述2个基本事件构成,简记为
例1.1.2 一射手向一目标射击3次,观察他的击中次数,可能为“击
中0次”,“击中1次”,“击中2次”,“击中3次”,即该试验有这4种可能结果,每一个结果都是一个基本事件,所以该试验所对应的样本空间可以
简记为
记A={至少有1次击中}={1,2,3} S;B={击中次数
不到2次}={0,1} S.A,B均为随机事件。
例1.1.3 记录一批标注重量为50(kg)的袋装大米的重量x与农药
残留量y,对应的样本空间为
其中y0
为农药最高残留量。
例1.1.4 从15个同类产品(其中12个正品,3个次品)中任取4个产
品,观察取得的次品数,则对应的样本空间为
{至少有2个正品}及{恰有2个正品}均为随机事件。
当某一事件所包含的一个样本点发生时,我们就称该事件发生。例
如,在例1.1.2中,A={1,2,3},若射手“恰好击中1次”时,即A所包
含的一个样本点出现,那么我们就称事件A发生;当射手“恰好击中2
次”时,我们亦称事件A发生;当射手“恰好击中3次”时,我们同样称事
件A发生。
特别地,若将样本空间S亦视为一事件,因为S包含了试验所有的可
能结果,因此在任何一次试验中,事件S一定会发生。我们称这种每次
试验必然发生的事件为必然事件,用S来表示。与之相对应地,称在任
何试验中都不可能发生的事件为不可能事件,记为?。考察例1.1.4中的2个事件:{4个都是次品}和{至少有1个正
品},前者是不可能事件,后者是必然事件。
(二)事件的相互关系及运算
在研究随机现象时,为了掌握复杂事件的统计规律,我们常常需要
研究事件之间的相互关系及运算。
前面我们已经用集合描述了样本空间与随机事件,下面我们再用集
合论的方法来定义与理解事件的相互关系及运算。
1.事件的包含与相等
设A,B为同一样本空间S中的两个事件。若当事件B发生时一定导
致A发生,则称事件A包含事件B,记为
,记
为A=B,即称事件A与B相等。
2.事件的运算
同样假设以下参与运算的事件都在同一样本空间中。
事件A∪B在集合论中理解为由集合A与B的元素合并到一起构成的
新的集合,现在A,B为随机事件,A∪B为一个新的事件。事件A∪B包
含了A和B的所有样本点,这些样本点发生时,A∪B发生。故当事件
A,B至少有一发生时,A∪B发生。因此有下面的定义:
为事件A与事件B的和事件。同样,称
为n个事件 的和
事件;称为可列个事件 的和事件。
而在集合论中,A∩B表示由A,B两个集合的公共元素组成的新的集
合,即A∩B发生当且仅当事件A,B同时发生。故称
为事件A与事件B的积事件,也可表示成A?B,或表示成AB。类似可以定
义:
为n个事件 的积
事件;称
为可列个事件 的积事件。
对于“A不发生”事件,称之为A的逆事件,记作 ,即
注意到 ,同时 。故A与 互逆,又称A与 为对立事件。
A与B的差事件,记为A—B,即
因此, 。
我们可以借助以下的图形(见图1.1.1),表示以上事件的关系和运
算:
图1.1.1
和、交与逆事件具有以下的运算规则:
交换律:;
结合律:;
分配律:;
德摩根定律(De Morgan's laws):即“n个事件至少有一发生”的逆事件为“这n个事件都不发生”;“n个事件
都发生”的逆事件为“这n个事件至少有一个不发生”。
定义1.1.1 设A,B为两随机事件,当AB=?时,称事件A与事件B
不相容(或互斥)。
也即当A与B不能同时发生时,称A,B不相容。我们注意到“样本空
间中的样本点两两不相容”。
例1.1.5 抛一颗骰子,设
,6.再设A={得到偶数点},B={得到奇数点},C={得到1点或
3点}。则
显然 ;又AC=?,故A与C不相容,又
,故A,B互逆。
概率论中常有以下定义:由n个元件组成系统,若有一个损坏,则
系统就损坏,此时称该系统为串联系统;若有一个不损坏,则系统不损
坏,此时称该系统为并联系统。例如,一个凳子是由4条腿、凳板、靠
背共6个部分组成,如果其中一个部分损坏,我们就认为这把凳子坏
了,那么这把凳子就是一个由6个部件组成的串联系统。
例1.1.6 由“个部件组成的系统,设。则有§1.2 频率与概率
(一)频率
前面已经提到,我们的目的是要研究随机现象的数量规律性,为此
我们首先提出频率的概念。
在一定的条件下,设事件A在n次重复试验中发生nA
次(称nA
为A在
这n次试验中发生的频数),称比值 为事件A在
这n次试验中发生的频率(frequency),记为 ,例1.2.1 从市场上抽查了某品牌的一种液态奶制品30件,其中有20
件被检出了某种物质含量超标,则事件“检出某物质含量超标”在这30
次试验中发生的频率为 。
事件A发生的频率越大,人们就会感到A发生的可能性越大,频率
越小,就有这一事件不易发生的感觉,所以频率是人们对事件发生的可
能性大或小的第一认识。
事件的频率具有以下性质:
(1)对任一事件 ;(2) ;
(3)当事件A与B不相容时,。
性质(3)可以推广,当
两两不相容时,例1.2.2 某厂每天从当天的产品中抽取50件,检查其是否合格,记
录于表1.2.1:
表1.2.1
表1.2.2
实验者 n n A fn
(A )
德摩根 2048 1061 0.5181
蒲丰 4040 2048 0.5069
K.皮尔逊 12000 6019 0.5016
K.皮尔逊 24000 12012 0.5005
例1.2.3 抛硬币试验,在相同的条件下将一枚硬币抛n次(你不妨
一试),设A={出现正面},当“较小时, 的变化范围
较大,但人们发现,当n渐渐增大时, 的值渐渐地稳定在0.5附近。以下是几个世界著名的大统计学家抛硬币的试验结果(列
于表1.2.2):
无数事实告诉我们,在大量试验中(即当n充分大时),任一随机
事件A的频率 具有稳定性, 会稳定于一个
常数p(0≤p≤1)附近,这个数是由事件A的属性所决定的。这给了我们
一个机会,一个用数量来描述事件A发生的可能性大小的机会。
(二)概率
有一种定义概率的方法(称之为概率的统计性定义)是:设某一随
机试验所对应的样本空间为S,对S中的任一事件A,A的频率
的稳定值p定义为A的概率,记为P(A)=p。
虽然上面的定义很直观,很易理解,且人们也常用这样的思路来解
释概率,但也存在问题。事实上,人们常常不易知道 的
稳定值p,因而我们采用以下公理化的定义。
定义1.2.1 设某一随机试验所对应的样本空间为S.对S中的任一事
件A,定义一个实数P(A),满足以下三条公理:
(1)P(A)≥0;
(2)P(S)=1;
(3)对S中的可列个两两不相容的事件
,有则称为P(A)为A的概率(probability),P(?)为概率测度。
值得注意的是,对于有限个两两不相容的事件的和事件有
以上定义的概率有以下性质:
(1) ;
因为 ,两边求概率(注意到),即得。
特别地, ,可得。
(注意:若有P(A)=0,不一定能得出A=?。)
(2)当 时,必有P(A)≥P(B);
因为当 时,。而 ,故P(A)≥P(B)。进而可得P(A)≤P(S)=1。
(3)概率的加法公式:性质3可以推广:
例1.2.4 设甲、乙两人向同一目标进行射击,已知甲击中目标的概
率为0.7,乙击中目标的概率为0.6,两人同时击中目标的概率为0.4,求
目标不被击中的概率。
解
而
,所以
例1.2.5 设甲、乙、丙三个人去参加某个集会的概率均为0.4,且
甲、乙、丙中至少有两个人去参加的概率为0.3,三人同时参加的概率
为0.05。求甲、乙、丙三人至少有一人参加的概率。
从以上两个例题可以看出,解这类题,第1步:要设随机事件;第2
步:要明确写出已知什么及要求什么;第3步:写出事件的运算式与概率运算式,求出概率。§1.3 等可能概型
在某些随机试验中,我们常假设样本空间中样本点出现的可能性相
等。例如,抛硬币试验,S={正面,反面},我们常假设出现正面与
反面的概率相等。
定义1.3.1 一个随机试验,如果满足下面两个条件;
(1)样本空间中样本点数有限(有限性);
(2)出现每一个样本点的概率相等(等可能性)。
则称这个试验问题为古典概型,又称等可能概型。
若设一等可能概型的样本空间为
,则由定义1.3.1知。任一随机事件。由样本点两两不相容的性质,知
这就是说,在等可能概型中,任一事件A的概率为
因此,在古典概型中,求随机事件概率的问题就可以转化为数样本
点数的问题,这常要用到组合数学。
例1.3.1 从一付牌(去掉两个王,共52张)中随机取两张,求“恰是一红一黑”的概率。
解 设A={恰是一红一黑}。
(1)>若是不放回抽样(即第一次抽出1张,不放回,再抽第二
张),则
(2)>若是放回抽样(即第一次抽出1张后,放回,再抽第二
张),此时的样本空间为
则
例1.3.2 (抽签问题)袋中有编号为1,2,…,n(n>1)的n个
球,其中有a个红球,b个白球(a+b=n)。从中每次摸一球,不放
回,共摸n次。设每次摸到各球概率相等。求第k(l≤k≤n)次摸到红球
的概率。
解 设Ak
={第k次摸到红球},k=1,2,…,n。
解法1 假设我们视n次摸出的球号的先后排列为一个样本点,则样
本空间中共有n!个样本点。由题意知,出现每一个样本点的概率相
等,而第k次为红球共有a(n-1)!个样本点。所以
解法2 若我们n个同学去摸球,我们只关心哪几个同学摸到红球为试验的结果,即假设视“哪几次摸到红球”为样本点,则样本空间总样本
点数为由题意知,出现每一个样本点的概率相等。如果Ak
发生,即第k
次一定为红球,只要在余下的(n—1)次中决定(a—1)次就行。故
解法3 若视第k次摸到的球号为样本点,则样本空间中共有n个样
本点,其中有a个样本点使得Ak
发生,故
以上三种方法计算得到:在抽签问题中,第k(l≤k≤n)次摸到红球
的概率与k无关。
例1.3.3 (配对问题)一个小班共有n个学生,分别编上1,2,…,n号,在中秋节前每人做一件礼物相应地编上1,2,…, n号。将
所有礼物集中放在一起,然后让每个同学随机地取一件(即,每次取到
每一件礼物是等可能的),求没有人取到自己礼物的概率。
解 先求“至少有一个人拿到自己的礼物”的概率。设
由概率的加法公式,得
如果将先后取到的礼物的编号(即排列)作为一个样本点,例如,(1,2,???,n)表示n人都取到了自己的礼物,那么共有n!个样本
点,由题意知出现每一个样本点的概率相等。当Ai
发生时,即i号配对其
余(n—1)个号可以任意的排列,故当n充分大时,上式的值近似于 。§1.4 条件概率
(一)条件概率
我们先来看一个例子,设一批产品的合格品率为80%,合格品中
90%是优质品,从中任取一件,设A={取到合格品},B={取到优
质品},则取到优质品的概率显然为72%。若把考虑问题的范围缩小,即,只考虑已知取到的一件是合格品,那么取到的这一件合格品是优质
品的概率应为90%,也就是说,如果把取到所有的合格品的概率记为
1,那么取到的一件是优质品的概率为90%,常记为P(B|A)=90%。
P(B)=72%与P(B|A)=90%是在两个不同的样本空间中对事
件B的概率进行度量,后者是将A作为新的样本空间。
定义1.4.1 如果P(A)>0,那A发生的条件下B的条件概率
(conditional probability)为
例1.4.1 将一枚均匀的硬币抛两次,已知“至少有1次正面”的条件
下,求“两次都是正面”的概率。
解 设Hi
={第i次为正面},i=1,2,B={至少有一次为正
面},C={两次均为正面}。
样本空间为。因为硬币是均勾的,故这是一个等可能概型。
解法1 显然
,故解法2 将B视为缩减了的样本空间S1
,则
这也是一等可能概型。在S1
的3个样本点中只有一个样本点使C发生,故
解法1是用条件概率定义求解,解法2是利用我们对条件概率的理
解,用缩减了的样本空间来求解,两种方法都行。
例1.4.2 一袋中有5个红球,4个白球,从中每次摸一球,不放回抽
样,抽4次。(1)已知前两次中至少有一次摸到红球,求前两次中恰有
一次摸到红球的概率;(2)已知第4次摸到的是红球,求第1次和第2次
摸到的都是红球的概率。
解 设Ai
={第i次摸到红球},i=1,2,3,4。再设B={前两次
中至少有一次摸到红球},C={前两次恰有一次摸到红球}。
(1)>题中要求的是P(C|B)。
(2)即求。由§1.3的例1.3.2,可知 。而
所以
其实,任何事件的概率都是在一定条件下给予的值,也即概率本身
就是有条件的。上面定义的条件概率无非是在新的样本空间下的概率度
量,因此条件概率同样具有一般的概率性质。
例如:当P(C)≠0时,有
(1) ;
(2)当 时,;
(3)。
推广之,(二)乘法公式
由条件概率的定义知,当P(A)≠0,P(B)≠0时,即两个事件积事件的概率等于一个事件的概率乘以在这个事件发生的条
件下另一个事件的条件概率,称此等式为概率的乘法公式。
推广之,当
时,有
为了证明(1.4.3)式,对等式的右边利用条件概率的定义,可得
对应于条件概率(假设以下的条件概率均有意义),则相应地有
例1.4.3 设一社区“3口之家”占了70%,且有40%的家庭“至少有1
人职业为教师”,在“3口之家”中有30%的家庭“至少有1人职业为教
师”。在这社区中随机找一户,(1)求这一户既不是“3口之家”又没有
教师的概率;(2)已知这一户没有教师,求这一户是“3口之家”的概
率。
解 设A={这一户是“3口之家”},B={这一户有教师},由题
意知,(1)P(A)=70%,P(B)=40%,P(B|A)=30%,得。
所要求的概率为
例1.4.4 某人参加某种技能考试,已知第1次考合格的概率为
50%,若第1次没有合格,通过努力,第2次能考合格的概率为60%;若
第1,2次均不合格,则第3次能考合格的概率为70%,求此人最多3次能
考合格的概率。
解 设Ai
={第i次考合格}i=1,2,3,B={最多3次能考合
格}。
解法1 注意到。所以
解法2 由于 ,故
(三)全概率公式、贝叶斯公式假设A,B为随机事件,那么总是有 ,又因为AB与 互不相容,可得
(1.4.6)式很重要,说明当直接计算A的概率比较困难时,可以先将A
分解成不相容的两部分Ab与 ,当然B常常与A有密切的关系。
它使得我们能够通过第二个事件b发生与否来求得A的概率。注意到
,故(1.4.6)式实际上是条件概率的加权平
均。式中重要的是如何寻找合适的B。
为了将(1.4.6)式推广至更一般的情形,下面先给出一个定义。
定义1.4.2 设S为某一随机试验的样本空间,为该试验的一组事件,且满足
则称 为S的一个划分,或称为S的一
个完备事件组。
上述定义中的两条,通俗而言,即 两同时发
生是不可能的,而至少有一发生又是必然的。其实,当样本空间S的样
本点有限时,这些样本点就是S的一个划分。
若A是S的一个事件, 是S的一
个划分,则参照导出(1.4.6)式的方法,我们也可以将A分解成两两不相容的事件的和,即
两边求概率,得 。于是
我们就可以得到下面的定理:
定理1.4.1 设S为某一试验的样本空间,A为该试验的事件。设
是S的一个划分,且。则
称(1.4.7)式为概率的全概率(total probability)公式。
同样(1.4.7)式的关键是找到一组合适的划分。
在上述定理的条件下,有
,故
当 ,n时,有
称(1.4.8)式为条件概率的全概率公式。
定理1.4.2 设S为某一试验的样本空间,A为该试验的事件,且P(A)≠0。设 是S的一个划分,且 。则对任意k
=1,2,…,n,称(1.4.9)式为概率的贝叶斯(Bayes)公式。
在利用贝叶斯公式时,其中的P(Bj)(j=l,2,…,n)的概率是
事先假设(或者根据以往的资料或是根据经验的累积)知道的,常称
P(Bj)为先验概率,而当事件A发生时,我们可以对Bj
发生的概率进行
重新认定(或修正),常称 为后验概率。
例1.4.5 某公司有甲、乙两人,已知甲近期出差的概率为0.7,又
已知如果甲出差则乙出差的概率为0.1,如果甲不出差则乙出差的概率
为0.6。(1)求乙近期出差的概率;(2)已知乙已经出差在外,求甲
近期出差的概率。
解。
(1)乙近期出差的概率为
(2)已知乙已经出差在外,求甲近期出差的概率为例1.4.6 设有3个箱子,第1箱装有3个白球和5个红球,第2箱装有2
个白球和2个红球,第3箱装有5个白球和2个红球。现随机地取一箱,再
在这一箱中随机取2次,每次取一球,不放回抽样。(1)求第一次取到
的是白球的概率;(2)已知第二次取到的是白球,问取到的是第1,2,3箱的概率分别为多少?
解 设Ai
={取到第i箱},i=1,2,3。Bj
={第j次取到白球},j
=1,2。那么A1
,A2
,A3
构成了样本空间的一个划分。
先来求 ,即在取到第1箱的条件下,第2
次摸到白球的概率。由§1.3例1.3.2知,,同理可得。从而 。故
同理其实,求P(B2)也可以用以下方法:
其中的。
另外,读者应该注意到 ,这一点事先就应知道。
例1.4.7 某地发生了一起当地人驾车偷盗事件,调查员有80%的把
握认为是男子A所为,现更有证据表明当事车为B型车,B型车在当地占
了30%。在已知男子A当天开的也是B型车的条件下,调查员认为男子A
偷盗的把握有多少?
解 设A={男子A为偷盗者},B={男子A当天开的是B型
车}。则
例1.4.8 有3个箱子,第1箱中装有5件为正品,2件为次品,第2箱
中有4件正品,2件次品,第3箱中有3件正品,2件次品。现从第1箱中随
机取1件放人第2箱,再从第2箱中随机取1件放人第3箱,再从第3箱中取
1件,求最后取出的是次品的概率。解 设A,B,C分别为从第1,2,3箱中取到次品事,易得。则
由条件概率的全概率公式知
同理可得
因此。§1.5 事件的独立性与独立试验
从§1.4中的一些例题可知,若A,B均为随机事件,一般情形下,不等于P(A)。也就是说事件B发生的条件会改变事件A发生
的概率。但也有不改变的,例如,某种彩票每次公布的最后两个数都是
从0到9这10个数字中随机取1个数,如果记Ai
={倒数第i位数小于
5},i=1,2,则有
,也就是说A1
发生并不影响A2
发生的可能性。由概率的乘法公式知,此
时
,易见此式中A1
,A2
是对称的。这时我们称A1
,A2
是相互独立的。
定义1.5.1 设A,B为两随机事件,当
成立时,称事件A,B相互独立(independence)。
定理1.5.1 当P(A)?P(B)≠0时,“事件A与事件B相互独立”等价
于“条件概率等于无条件概率”,即
定理1.5.2 当事件A与事件B相互独立时,均相互独立。
证明 因为 ,两边求概率并移项得当事件A与事件B相互独立时,故A与 互相互独立。由此可进一步得 均相
互独立。
定义1.5.2 设A,B,C为三个随机事件,当
都成立时,称事件A,B,C两两独立。
如果同时还满足P(ABC)=P(A)?P(B)?P(C),则称事件
A,B,C相互独立。
应注意到相互独立一定是两两独立的,而两两独立时不一定是相互
独立的。
例如,设一随机试验的样本空间为
,且是等可能概型,记。那么有。同理有
两两独立。不互相独立。
定义1.5.3 设n个事件
,若对任意的
,都有
成立,则称事件
相互独立。
如果对于可列个事件,若其中任意的有限个事件相互独立,则称这
可列个事件相互独立。
最后,我们来定义试验的独立性,假设所考虑的概率试验是由一系
列子试验组成。例如,某一种彩票一期一期地不断开奖,就可以把每一
次开奖看作一个子试验,而且这一期开奖的结果不影响其他期的开奖结
果。像这样的试验结果互不影响的一系列试验称为独立试验。如果各个
子试验是在相同条件下进行的,那我们就称这些试验为重复试验。
在实际问题中,我们常常不是用独立的定义去验证事件的独立性,而是根据实际情况来判断。例如,我们可以认为某一批袋装味精的重量
(克)与纯味精的含量(%)是独立的;又如,甲、乙两人同时向各自
的靶位射击,注意这儿的“同时”两字,这就意味着两个人的射击结果是
互不影响的,所以事件“甲命中”与“乙命中”是相互独立的。
图1.5.1
例1.5.1 有5个独立元件组成的系统(如图1.5.1所示),设每个元件运行正常的概率为户p,0
率。
解 设Ai
={第i个元件运行正常},i=1,2,3,4,5。由题意
知, 相互独立。并设A={系统
运行正常},则 ,那么
图1.5.2
用缩减了的样本空间理论求解 的值为p1
,p2
即为图1.5.2所示系统运行正常的概率,故
又若记 的值为p2
,p2
即为图1.5.3所示系统运行正常的
概率,同理可得图1.5.3
所以
例1.5.2 一袋中有编号为1,2,3,4共四个球,每回从袋中有放回
地取两次(一次一个球,假设取到每一个号码的概率相等),并记录号
码之和。这样独立重复地试验,求“和等于3”出现在“和等于5”之前的概
率。
解 设A={“和等于3”出现在“和等于5”之前},B={第一次号码
之和为3},C={第一次号码之和为5},D={第一次号码之和既不
是3,也不是5}。
显然每次“号码和为3”的概率为 ,“号码和为5”的概率为
,“号码和既不是3又不是5”的概率为 ,故
由全概率公式,得在已知第一次号码和既不是3,也不是5的条件下,求A的条件概率问
题,相当于重新开始考虑A的概率,因为试验是独立的,即第一次结果
不影响A发生的概率,所以P(A|D)=P(A),故
例1.5.3 某技术工人长期进行某项技术操作,他经验丰富,因嫌按
规定操作太过烦琐,就按照自己的方法进行,伹这样做有可能发生事
故。设他每次操作发生事故的概率为p,0
次操作。求:(1)n次都不发生事故的概率;(2)至少有一次发生事
故的概率。
解 设A={n次都不发生事故},B={n次中至少一次发生事
故},Ci={第i次不发生事故},i=1,2,…,n。由题意知,相互独立,且。故
注意到, ,也就是说,虽然每次发生事
故的概率p很小,但只要次数多(n充分大),至少有一次发生事故的概
率就会大,甚至接近于1总之,随着独立重复试验次数的增多,“小概率
事件”“至少有一次发生”的概率在渐渐增大。思考题一
1.设A,B为两随机事件,当P(AB)=0时,A与B不相容,对
吗?
2.随机事件A的频率 是个变化着的数,而概率P(A)
是一个定数,对吗?当n充分大时, ,对吗?
3.试举例说明P(AB)与P(B|A)的不同意义。
4.因为随机事件A发生时A∪B一定发生,故P(A|A∪B)=1,对
吗?
5.当 时,随机
事件A,B独立与不相容可能同时成立吗?A,B独立能用Venn图(见图
1.1.1)表示吗?
6.设随机事件A,B,C满足P(ABC)=P(A)?P(B)
·P(C),问A,B,C一定相互独立吗?习题一
1.为了解吸烟(草)对人体健康是否有影响,对一社区居民进行
抽样调查,分别用0,1,2表示不吸烟,少量吸烟及吸烟较多,再
用a,b,c表示身体健康,一般及有病。例如:(0,a)就表示抽到的
居民是不吸烟的健康者。
(1)问试验的样本空间共有多少个样本点?
(2)设A={抽到的居民身体健康},试写出A所包含的样本点;
(3)设B={抽到的居民不吸烟},试写出B所包含的样本点。
2.设A,B,C为3个随机事件,请用事件的运算关系式表示:
(1)A,B,C至少有2个发生;
(2)A,B,C最多有1个发生;
(3)A,B,C恰有1个不发生;
(4)A,B,C至少有1个不发生。
3.设A,B为2个随机事件,判断以下说法的对错,并说明理由。
(1)
,则一定有A,B不相容;
(2)P(A)=1,则一定有A=S;
(3)P(B)=0,则一定有B=?;
(4)P(A)=0.6,P(B)=0.7,则A,B一定相容。
4.设事件A与B不相容,P(A)=0.3,P(B)=0.6。求:(1)A与B至少有一发生的概率;
(2)A与B都不发生的概率;
(3)A不发生同时B发生的概率。
5.设A,B,C为3个随机事件,已知P(A)=P(B)=P(C)=
0.4,且A,B,C至少有2个发生的概率为
0.3,A,B,C同时发生的概率为0.05,求A,B,C都不发生的概
率。
6.一袋中有10个球,其中8个是红球。每次摸一球,共摸2次,在
放回与不放回抽样两种方式下,分别求:
(1)“两次均为红球”的概率;
(2)“恰有1个红球”的概率;
(3)“第2次是红球”的概率。
7.一30人的班级中有两个“王姓”的学生,将全班学生随机排成一
排,求:
(1)两个“王姓”学生紧挨在一起的概率;
(2)两个“王姓”的学生正好一头一尾的概率。
8.一盒子中有2个红球,3个黑球,2个白球(共7个球)。每次摸
一球(不放回),共摸3次。求:
(1)摸到球恰是1红1黑1白的概率;
(2)摸到的全是黑球的概率;
(3)第1次为红且第2次为黑球第3次为白球的概率。
9.编号为1,2,…,9的9辆车,随机地停入编号为1,2,…,9的
9个车位中,若车号与车位号一样称该车配对。求:(1)1号车配对的概率;
(2)1号车配对而9号车不配对的概率;
(3)1号车,9号车都配对,但其他均不配对的概率。
10.设A,B为两随机事件,且已知
,求:
(1) ;
(2) ;
(3) 。
11.设一社区订A,B,C报的家庭分别占50%,30%,40%。且已
知一家庭订了A报的条件下再订B报的概率为20%,订了C报的条件下又
订A报或B报的概率为60%。随机找一家庭,求该家庭至少订A,B,C报
中的一种的概率。
12.某企业中有45%为女职工,10%的职工在管理(技术,质量,行政)岗位。5%的职工为管理岗位的女职工。在该企业中随机找一位
职工。
(1)>已知该职工为女职工的条件下,求该职工在管理岗位的概
率;
(2)>已知该职工在管理岗位,求该职工为男职工的概率。
13.从1,2,3,4,5中取一数X,再从1,2,…,X中取一数Y,求{Y=2}的概率。
14.一架子上有4把枪,其中3把是调试好的,1把未调试。设某君用调试好的枪射击命中率为60%,用未调试的枪命中率为5%。此人从4
把枪中随机地取一把进行射击。
(1)求命中的概率;
(2)已知此人命中了,求取到的是未调试的枪的概率。
15.对某证券营业点进行统计。得知入市时间在1年以内的股民
赢、平、亏的概率分别为10%,20%,70%;人市时间在1年以上但不
到4年的股民赢、平、亏的概率分别为20%,30%,50%,入市时间于4
年的股民赢、平、亏的概率分别为50%,30%,20%。不同入市时间的
股民数分别占40%,40%,20%。今在该营业点随机找一股民。
(1)求其有赢利的概率;
(2)若已知其亏损了,问他为新股民的概率有多大?
16.有两组同类产品,第一组有30件,其中有10件为优质品;第二
组有20件,其中有15件为优质品今从两组中任选一组,然后从该组中任
取2次(每次取1件,不放回抽样)。
(1)求第1次取到的是优质品的概率;
(2)在已知第2次取到的是优质品的条件下,求第1次取到的不是
优质品的概率。
17.设一股票(股价以收盘价计)当今天(记为第1天)是涨的情
形下第2天是涨(1个单位),跌(1个单位),平(基本持平)的概率
为 ;当今天是跌(或是平)的情形下上述三种情况发
生的概率分别为 。
即明天的情况只与今天有关。其中。已知该股票今天是涨的。
(1)求第3天与今天持平的概率p1;(2)第4天股价比今天涨了2个单位的概率p2。
18.试证:当O
19.设A,B,C为随机事件,P(A)>0,P(B)>O,P(C)>
0。请说明以下说法对,错或可能对。
(1)A,B相互独立,则A,B相容;
(2)P(A)=0.6,P(B)=0.7,则A,B独立。
(3)P(ABC) =P(A)?P(B)?P(C),则A,B,C相互独
立。
(4)A,B不相容,则A,B不独立
20.由4个独立部件组成的一个系统,第i个部件工作正常的概率为。且已知至少有3个部件工作正常时系统工作正
常。
(1)求系统工作正常的概率α;
(2)在系统工作正常的条件下求4个部件均工作正常的概率β;
(3)对系统独立观察3次,求系统恰有2次工作正常的概率γ。
21.连续抛一枚硬币,p表示每次出现正面的概率,记。求:
(1);
(2) ;
(3) 。
22.已知一批照明用灯管使用寿命大于1000小时的概率为95%,大
于2000小时的概率为30%,大于4000小时的概率为5%。
(1)已知一灯管使用了1000小时没有坏,求其使用寿命大于4000
小时的概率;
(2)取10个灯管独立地装在一大厅内,过了2000小时,求至少有3
个损坏的概率。
23.一系统的外加电压有99%的时间是正常的,当外加电压正常时
系统稳定的概率为90%,当外加电压不正常时系统稳定的概率为20时。
且已知当系统稳定时元件正常工作的概率为80%,当系统不稳定时元件
不能正常工作的概率为90%。
(1)求元件能正常工作的概率;
(2)若该系统有5个独立工作的元件,求至少有一个元件不能正常
工作的概率。第二章 随机变量及其概率分布
§2.1 随机变量
随机试验的结果常有两类:示数的和示性的。例如,观察某一车间
的用电量;观察某一区域一天内发生的交通事故次数;记录一天内一手
机收到的短信数;气象上的温度及相对湿度,等等,其结果均可用一数
来表示。我们称这些试验的结果为“示数的”,但也有大量的随机试验的
结果却不然,例如,抛一枚硬币,其结果可能是正面或反面;记录新生
儿的性别,其结果是男或女;检验一件产品,它可能是一等品、二等
品、等外品,等等,我们称这类试验的结果为“示性的”。为了用更多的
数学方法来描述与研究随机现象,必要时人们常常将示性的结果数量
化,即定义一个实数与示性的结果相对应。
同时,相对于随机试验的实际结果而言,有时我们更感兴趣这些结
果的某些函数,例如,观察某一地区新生儿的性别,我们感兴趣于男
婴、女婴的数量,同时也感兴趣于两者的数量之差。又如,我们观察一
运动体的速度的随机变化,我们还感兴趣于随之产生的运动体的动能的
变化情况。由上面这些例子可以看到,我们感兴趣的量是随机试验的结
果的实值函数,我们称它为随机变量。通俗说,随机变量就是随随机试
验结果而变的量。一般地,有下面的定义。
定义2.1.1 设随机试验的样本空间为S={e},若X=X(e)为定义
在样本空间S上的实值单值函数,则称X=X(e)为随机变量(random
variable)。
如果随机试验的结果是示数的,则样本点e即为一实数,这时常定
义X=X(e)=e。
本书中常用大写英文字母
来表示随机变量,而以小写字母表示实数。
引入了随机变量,一方面使我们能够用随机变量来描述随机现象,另一方面也可以同时用研究随机变量取值的概率来代替随机现象发生的
概率。
例2.1.1 一枚硬币抛4次,设每次出现正面的概率为p(0
1),记X为4次中出现正面的次数,而4次中首次出现正面在第Y次(如
果4次都没有出现正面,则取i=0)。试分别写出X与Y的所有可能取值
与取每一值的概率。
解 首先,易得X与Y的所有可能取值均为:0,1,2,3,4.设。由题意知,。得
Y取每一值的概率分别为:而且,我们可以验算得到。
例2.1.2 某销售员独立地向编号为1,2的两顾客推销售价分别为
17.3万与18.7万的A,B两款小轿车,与这两位顾客成交的概率分别为0.4
与0.7。设每位顾客选择A,B两款车型的概率相等,试给出该销售员的
成交额X的可能取值与取每一值的概率〔假定每位顾客最多买一辆)。
解 由题意知,X的可能取值为:0,17.3,18.7,34.6,36,37.4.
设
由于对编号为1,2的两顾客是独立推销的,因此两位顾客的购买行为是
独立的,也就是说, 都是独立的,同理, 也都是独立的。而且。因此§2.2 离散型随机变量
若随机变量的取值为有限个或可列个,则称此随机变量为离散型
(discrete)随机变量,简称离散量。
例如,§2.1中的例2.1.1与例2.1.2中的随机变量取值均为有限个,故
它们均为离散型随机变量。又如,抛一枚硬币,直到正面首次出现所需
的抛掷次数,一个广场上的人数等等,这些量可能没有上限,但均可
列,所以这些量也是离散型随机变量。若以X记某一地区成年男子的身
高,以Y记某产品的寿命,显然X与Y的取值充满着某一区间,它们的可
能取值不能一一列出,所以X与Y不是离散量。
离散量的统计规律通常用概率分布律来描述。
设X为离散量,若其可能取值为
,则称
为X的概率分布律(distribution sequence)。
概率分布律也可用下面的列表方式来表示:
概率分布律有以下两条性质:。
性质(1)是显然的。性质(2)是因为是不同的样本点,即对
是两两不相容的,这样就得到了性质(2)。
例2.2.1 随机变量X的概率分布律为
求常数c的值。
解 这里先回忆一下高等数学中的一个函数展开式。由概率分布律的性质知,那么 。
以下介绍几个重要的离散量。
(一)0-1(p)分布
若随机变量X的概率分布律为其中,0
用记号X~0-1(p)表示(也可表示为B(1,p))。
例如:若某一地区每一个新生儿是男(或女)的概率为。0.51(或
0.49),记{X=1}为男孩,{X=0}为女孩,则X~0-1(0.51)。
(二)二项分布
若随机变量X的概率分布律为
其中, ,则称X服从参数为(n,p)
的二项(binomial)分布,且记为 。
显然,(2.2.2)式中
,且
在讨论二项分布时必须提到下面的重要试验。
定义2.2.1 在n次独立重复的试验中,每次试验都只有两个结果:,且每次试验中A发生的概率不变,记
,称这一系列试验为n
重贝努里(Bernoulli)试验。
例如,若考虑一个试验的结果只有成功与失败,且每次成功的概率
都为p,O
验.又如,独立重复地抛n次硬币,每次结果只有正面或反面;在一放
有红球与其他颜色的球的袋中有放回地摸球n次,每次只记录摸到红球
与其他球(非红球)两种结果,且设每次摸到红球的概率是p,O
1,等等,都可以看成是n重贝努里试验。
在n重贝努里试验中,若记事件A发生的概率为P(A)=p,O
1。设X为在n次试验中A发生的次数,则X~B(n,p),即
因为事件{X=k}即为“在n次试验中恰有k次A发生且有。n-k次A不发
生”,这k次可以是n次中的任意k次,故有 种方式,而每一“特定
的k次A发生且特定的(n-k)次A不发生”的概率为
,这样就得到了(2.2.2)式。读者可以再
详细地看一下§2.1例2.1.1中随机变量X的概率分布律的求解过程。特别
地,当n=1时,B(1,p)即为。0-1(p)分布。
例2.2.2 由6位品酒师独立投票评定某种酒是否为优质酒,若6位中
有4位投票同意,则定该酒为优质酒,且设每位品酒师作出正确判断的
概率为p,0
(1)若该酒为优质酒时,能作出正确判断的概率α。(2)若该酒
不为优质酒时,能作出正确判断的概率β。
解(1)当该酒为优质酒时,至少要有4位品酒师作出正确判断才能
判定此酒为优质酒,所以(2)当该酒不是优质酒时,则至少要有3位品酒师作出正确判断,所以
例2.2.3 设有一大批优质品率为p的产品,O
进行验收:第一次先从中随机取5件,若至少有4件是优质品则接收该批
产品,若优质品不到3件就拒收;否则再第二次从中抽2件,若2件均为
优质品就接收,否则就拒收。求:(1)第一次抽样就接收该批的概率
α。(2)该批产品被接收的概率β。
解 由题意知,各次抽样结果相互独立(由于是一大批,总的数自
很多)。设X为第一次抽到的优质品数,Y为第二次抽到的优质品数,显
然 。
一般情形下,当n不是很大的时候,对于二项分布的计算还是比较
容易的,但当n比较大的时候,二项分布的概率值可以采用Excel计算。
例2.2.4 假设 ,现分别计算P(X≤10)和P(X=10)。
解 先计算P(X≤10),由二项分布可知:显然这个计算不是很简单,但可以通过Excel表单简单得出。具体如
下:在Excel表单的任一单元格输入 在主菜单中点
击“插入” “函数(F)” 在选择类别的下拉式菜单中选
择“统计” 选择“BINOMDIST”点击”确定” 在函数参数
表单中输入“Number_s=10,Trial=100,Probability_s=0.05,Cumulative=TRUE”,然后点“确定” 即在单元格中出
现“0.98852759”。
如果要计算P(X=10),则只需要在上面的过程中所有的步骤中
把“Cumulative=TRUE”改“Cumulative=FALSE”。即在单元格中出
现“0.016715884”。
(三)泊松分布
若随机变量X的概率分布律为
其中λ>0,则称X服从参数为λ的泊松(Poisson)分布,且记为。
观察(2.2.3),显然有对任意的
,且由§2.2的例2.2.1知,。
参数λ的含义将在第四章中说明,而有关泊松分布的数学模型将在随机过程第十二章中研究。
泊松分布有着非常广泛的应用.这是因为当n足够大,p充分小(一
般要求p<0.1),且np保持适当大小时,参数为(n,p)的二项分布可
用泊松分布近似描述。
设X~B(n,p),并记λ=np。则
当n充分大和适当的λ时,也就是说,当n充分大,p足够小时,根据统计工作者的经验,以下的随机变量常可近似用泊松分布描
述:
1.某产品的不合格点数;
2.一本书一页上的印刷错误数;
3.一手机某一时间段内收到的信息次数;
4.某放射物在一定时间内放射出的α粒子数;
5.一定的时间区间内进入某书亭的人数。例2.2.5 设某公共汽车站单位时间内候车人数X服从参数为4.8的泊
松分布。求;(1)随机观察1单位时间,至少有3个人候车的概率;
(2)随机地独立观察5个单位时间,恰有4个单位时间至少有3人候车的
概率。
解 (1)由题意知,X~π(λ),其中λ=4.8则
(2)设被观察的5个单位时间内有Y个单位时间是“至少有3个人候
车”,则Y~B(5,p),其中p=P{X,≥3}=0.8575。那么
例2.2.6 某地区一个月内每200个成年人中有1个会患上某种疾病,设各人是否患病相互独立。若该地区一社区有1000个成年人,求某月内
该社区至少有3人患病的概率。
解 记p=1200,且设该社区1000人中有X人患病。由题意知,X~
B(1000,p),记λ=1000p=5。利用(2.2.4)式,所要求的概率为
例2.2.7 例2.2.6的计算可以通过Excel表单简单得出。先计算出
P{X≤2}具体如下:在Excel表单的任一单元格输人“=” 在主
菜单中点击“插入” “函数(F)” 在选择类别的下拉式
菜单中选择“统计” 选择“POISSON”点击“确定” 在函
数参数表单中输人“X=2,Mean=5,Cumulative=TRUE”,然后点“确定” 即在单元格中出现“0.124652019”。P{X≥3}=1
-P{X≤2}=0.875347981。
(四)其他离散型随机变量
例2.2.8 一袋中共有N个球,其中有a个白球与b个红球(a+b
=N)。从中不放回地取n(n≤N)个球,设每次取到各球的概率相等。
若其中有X只白球,试写出X的概率分布律。
解 这是一个等可能概型,其中。
如果随机变量X具有形如(2.2.5)的概率分布律,则称X服从超几
何(hypergeometric)分布。
例2.2.9 设独立重复试验中,每次试验有两个结果: 。
每次试验中A出现的概率不变,记P(A)=p,0
发生时所需的试验次数为X,求X的概率分布律。
解 参照§2.1的例2.1.1中求Y的概率分布律的方法,可知
如果随机变量X具有形如(2.2.6)的概率分布律,则称X服从参数
为p的几何(geometric)分布。§2.3 随机变量的概率分布函数
前面我们介绍了离散型随机变量及其概率分布律。但实际上也有许
多随机变量的取值是不可列的,因此就不能用概率分布律来描述其概率
分布规律。例如,打靶时弹着点离开靶心的距离;一地区成年男子的身
高;一批产品的寿命;在职职工个人月收入,等等,这些量均不可列,不是离散量。事实上,我们也不关心这类量取某一定值的概率,而是关
心其落在某些区域的可能性大小。例如,我们可能会关心事件“打了8环
以上”,“身高大于170cm”,“寿命大于1000小时且小于2000小时”,“职
工月收入低于3000元”的概率。下面我们引入概率分布函数的概念。
定义2.3.1 设X为一随机变量,x为任意实数,函数
称为随机变量X的概率分布函数,简称分布函数(distribution
function)。
对任意的实数 ,有
这说明X落在区间 的概率为两端点分布函数值之差。
也就是说,如果X的分布函数F(x)已知,则可以求出事件
的概率。从这个意义上说明,F(x)能完整地描述X的概率分布。
图2.3.1
几何地来看分布函数,将X设想成一随机点,那么X落在区间(-
∞,x]上的概率即为F(x)(如图2.3.1所示)。当X为离散量时,设X的概率分布律为。
则X的分布函数为
即F(x)为满足 的一切xi
的相应的概率之和。
例2.3.1 随机变量X~0-1(p)分布,0
分布函数及其图形;(2)P{X≥1}的值。
解 (1)由题意知,X具有概率分布律
那么X的分布函数为
(2)。
概率分布函数的性质:
(1)F(x)单调不减;这一点由(2.3.2)式即可知,当
,因此 。
(2)0≤F(x)≤1,且有
,简记为F(-∞)=F(+∞)=1。
因为F(x)为事件{X≤x}的概率,所以有0≤F(x)≤l。
又可设想有实数数列
越
小,事件 越来越接近不可能事件,故有F(-
∞)=0。用同样的方式可以理解F(+∞)=1。
(3)F(x+0)=F(x),即F(x)是右连续函数(证略)。
图2.3.2例如本节例2.3.1中的F(x)(见图2.3.2)在x=0,1点上为右连
续,在其他点上均为连续函数。
图2.3.3
例2.3.2 设一醉汉在A,B两点间移动,A,B两点间的距离为3个单
位。A,B两点有障碍物,他停留在A,B两点的概率均为14。设他离
开A的距离为X,且落在A,B两点间任一区间的概率与区间长度成正
比,求X的概率分布函数。
解 由题意知,P{X=0}=P{X=3}=14。
设比例常数为k,则
得k=16。显然有,当:x<0时,F(x)=0;
当x=0时,F(x)=14;当x≥3时,F(x)=l。而当0
接下来我们关注一类重要的非离散型随机变量——连续型随机变
量。
定义2.4.1 对于随机变量X,若存在一个非负的实函数f(x),使X
落在任一区域D上的概率
则称X为连续型随机变量,简称连续量。称f(x)为X的概率密度函数
(probability density function),简称密度。
由定义知,密度函数具有以下性质:
(1)f(x)≥0;
(2) ;
(3)X的概率分布函数;
(4)在f(x)的连续点x处, 。
由(2.4.1)式可知X属于区域D的概率等于概率密度函数在区域D上
的积分。令D=[a,b],则有上式中,若令a=b,则有
即,连续型随机变量取任一定值的概率为零。因此连续量落在开区间与
相应的闭区间上的概率相等。
例2.4.1 设X为连续型随机变量,其密度函数为
求(1)常数c的值;(2)P{X<0.5}的值。
解 (1)由概率密度的性质(2)可知,得c=32。
例2.4.2 一电子产品的无故障工作时间X(以小时计)为连续型随
机变量,其密度函数为求(1)常数λ的值;(2)从大批该种产品中抽取3只,恰有一只无故障
工作时间小于1050小时的概率。
解 (1)由于
,于是可得λ=11000。
(2)注意到
设3只产品中有Y只寿命小于1050小时,由题意知,Y~B(3,0.6321),那么所要求的概率即为
例2.4.3 一银行服务需等待,设等待时间X(以分钟计)的概率密
度为
某人进了银行,且计划等下还要去办另一件事,故打算先等待,如果15
分钟后还是没有等到服务就离开银行,设此人在银行实际等待时间
为Y。(1)求Y的概率分布函数;(2)问Y是离散量吗?Y是连续量
吗?
解 (1)由分布函数的定义知,Y的概率分布函数为显然,当y≤0时,F(y)=0;当y≥15时,F(y)=l;当0
(2)因为Y的取值范围为[0,15],Y的取值不可数,所以Y不是
离散量。又
,即Y取定值15时概率不为零,所以Y亦不是连续量。因此Y是既非离散
又非连续的随机变量。
本教材主要研究离散量与连续量。
下面我们研究几种重要的连续量。
(一)均匀分布
定义2.4.2 设随机变量X具有概率密度
则称X服从区间(a,b)上均匀(uniform)分布,常记为X~U(a,b)。
显然上面的密度函数满足。
根据密度函数的定义,可知X的概率分布函数为
均匀分布密度函数 均匀分布分布函数
图2.4.1
设有实数c,l,满足 ,则有
上式的值与c无关,即X落在区间[a,b]内任一长度为l的子区间的概
率为子区间的长度与(b-a)的比(即几何测度之比),其概率与l成
正比,而且仅依赖于子区间的长度,与子区间的位置没有关系。
例2.4.4 杭州某长途汽车站每天从早上6:00(第一班车)开始,每隔30分钟有一班车发往上海。设王先生在早上6:20过X分钟到站,且
设X服从(0,50)上均匀分布。(1)求王先生候车时间不到15分钟的概率;(2)如果王先生一个月中有两次按此方式独立地去候车,求他
有一次候车不到15分钟,另一次候车大于10分钟的概率。
解 X~U(0,50),由题意知,只有当王先生在图2.4.2中画阴影
的时间区间内到达时,候车时间会小于15分钟,图2.4.2
阴影区间的长度为25,所以
(2)同样可知,如果王先生在6:30以后至6:50之间或7:00至
7:10之间到达车站,则他的候车时间要大于10分钟,所以
设
那么所要求的概率为
(二)正态分布
正态随机变量是概率论与数理统计中最重要的随机变量。
定义2.4.3 设随机变量X具有概率密度其中参数 ,则称X服从参数为(μ,σ)的正态(normal)分布,或简称X为正态量,记为。
其相应的分布函数为
显然,f(x)≥0。下面来证明。
记
,作积分变量变换,令 ,则
于是通过将积分变量变换成极坐标形式,得
这样就得到I=1。
正态密度f(x)具有以下性质:
(1)f(x)关于x=μ对称;
(2) ;
(3) 。
图2.4.3 正态分布概率密度
由图2.4.3所示的密度曲线图可知,X的取值是中间(μ附近)大,两
头(离μ远的地方)小,而且是对称的(关于x=μ)。
人们常称正态变量的参数μ为位置参数,因为μ给出了密度对称轴的
位置及X的取值集中的位置;称σ为尺度参数,因为密度曲线的尺度(图
形的形状)完全由σ决定(却与μ无关)。
σ越大,曲线峰越低,越扁平,X在μ附近取值的概率(即相应的曲
边梯形的面积)越小,即X取值越分散,故σ是反映X取值分散程度的一
个指标量。
特别地,当μ=0,σ=1时,若记这时的正态量为Z,Z~N(0,1),称Z服从标准正态分布(standard normal distribution),其概率
密度为:
标准正态概率密度 标准正态分布函数
图2.4.4
其相应的分布函数为显然标准正态密度关于y轴对称,由此可得,对于任一实数:x>0
同时,当 时,对于任意的实数a,b,a
作积分变量变换,令 ,得
此时的被积函数为标准正态密度,故有
这样将正态变量的概率计算归结为标准正态分布函数值的计算问题。而
这些数值可查本书附表2。
若 ,由(2.4.5),(2.4.6)式可得
当k=1,2,3时,查附表2可得
图2.4.5
可以发现,以上概率值与μ,σ的取值无关(总结在图2.4.5中)。
例2.4.5 用天平称一实际重量为a的物体,天平的读数为随机变量。当σ=0.01时,(1)求读
数与a的误差小于0.005的概率;(2)求读数至少比a多0.0085的概率;
(3)若重复称3次,求3次中恰有1次“读数与a的误差小于0.005”的概
率。
解 (1)由(2.4.6)式,并查附表2,得
(2);
(3)设3次中有Y次“读数与a的误差小于0.005”,则Y~B(3,0.3830),因此
例2.4.6 上例的计算中正态分布的值可以通过Excel表单简单得
出。例如计算P(X-a<0.0085),具体如下:在Excel表单的任一单元
格输人“=” 在主菜单中点击“插入” “函数(F)”
在选择类别的下拉式菜单中选择“统计” 选
择“NORMDIST”点击“确定” 在函数参数表单中输人“X=
0.0085,Mean=0,Standard_dev=0.01,Cumulative=TRUE”,然后
点“确定” 即在单元格中出现“0.802337508”。
例2.4.7 设一天中经过一高速公路某一入口的重型车辆数X近似服
从 ,已知有25%的天数超过400辆,有33%的天数不
到350辆,求μ,σ。
解 已知P{X>400}=0.25,P{X<350}=0.33,查表得
在自然界与社会现象中许多量可用(或近似用)正态量来描述,那
些我们经常可以看到的(自然形成的)沙堆、谷堆、煤堆以及远处的某
些山的轮廓线,常常会让人们联想到正态密度曲线。我们身边的许多
量,如同一年龄段的人的身高,体重(但视力测量值不是正态量);一
个地区某一时段的降雨量;某公司普通职工的收入;医院里许多化验的
指标量等等,一般均可将其视为正态量,在第五章中我们还可以看到正
态量的更多应用。(三)指数分布
定义2.4.4 设随机变量X具有概率密度
其中λ>0,则称X服从参数为λ的指数(exponential)分布,记为X~
E(λ)。
显然有。
其相应的分布函数为
当X~E(λ)时,对任意的 ,我们有
或写成。
若将X看成某电子产品的寿命(以小时计),则(2.4.10)式可解释
为:“在已知产品用了 小时没有坏的条件下,再用t小时不坏”的条件
概率等于这产品“最初使用t小时不坏”的概率。形象地说这产品“忘却”了“已使用 小时”。所以常将(2.4.10)式形象地称作指数分布
的“无记忆性”。
指数分布概率密度
图2.4.6
例2.4.8 设一地段相邻两次交通事故间隔时间(以小时计)X服从
参数λ=16.5的指数分布。(1)求8个小时内没有发生交通事故的概
率;(2)已知已过去的8个小时中没有发生交通事故,求在未来的2小
时内不发生交通事故的概率。
解 (1)X~E(λ),λ=16.5,则
(2)由(2.4.10)式知
有人说指数分布的无记忆性不好理解,但看了例2.4.8(2)中的等
式
后就有点感觉了吧!
例2.4.9 有编号为1,2,3的3个同类设备。已知它们正常运行时间均服从参数为λ的指数分布。现1号,2号设备已在一系统中独立运行,当其中1台损坏时由3号接替运行。求3个设备运行到最后的不是3号设备
的概率。
解 不妨设1号先损坏,由于指数分布具有无记忆性,由3号接替后
开始考虑2号再正常运行t单位时间的概率应与3号正常运行t单位时间的
概率相等,所以得到“运行到最后的不是3号设备”的概率应为12。
(四)其他连续型随机变量
定义2.4.5 设随机变量X具有概率密度
其中参数α>0,β>0,则称X服从参数为(α,β)的Г(Gamma)分
布,记为X~Г(α,β)。
(2.4.11)式中的。特别地,当n为正整数时,有。
定义2.4.6 设随机变量X具有概率密度
其中参数α>0,γ>0,则称X服从参数为(>α,γ)的二参数威布尔
(Weibull)分布。
定义2.4.7 记随机变量X具有概率密度其中参数a>0,b>0,则称X服从参数为(a,b)的β(Beta)分布,记为X~β(a,b)。§2.5 随机变量函数的分布
在实际问题中,我们常会碰到已知一随机变量的分布,要求这一变
量的函数的分布问题。例如,已知到达车站的时间服从某一区间上的均
勾分布,要求候车时间的分布;已知半径测量值为正态分布,要求对应
的圆面积的分布,等等。本节要研究一个随机变量函数的分布问题。即
已知X的分布,Y=g(X),要求Y的分布。下面先来看几个例题。
例2.5.1 抛一枚骰子,当点数不大于3时定义Y=-1,当点数为4或
5时定义Y=0,当点数为6时定义Y=l。且记Z=Y2。(1)求Y的概率分
布律;(2)求Z的概率分布律。
解 (1)设抛一枚骰子得到的点数为X。由题意知当且仅当
{X≤3}发生时{Y=-1}发生,我们称事件{X≤3}与事件{Y=-
1}等价。同理事件{X=4}∪{X=5}与{Y=0}等价,事件{X=
6}与{Y=l)等价。故有
即
(2)由题意知 的可能取值为0,1。与(1)的解
法相同,得例2.5.2 设一商店某一批电子产品使用寿命(以小时计)X~
E(λ),λ=l250。商店对该批产品实行先使用后付款的办法销售。若
使用寿命小于100小时,顾客不用付费;若使用寿命大于100且小于250
小时,顾客得付10元;若使用寿命大于250小时,则要付30元。求顾客
付费的概率分布律。
解 设顾客付费的金额为Y元,Y的可能取值为:0,10,30。由题
意知X~E(λ),λ=1250。由于电子产品使用寿命小于100小时,顾客
不用付费,那么
同理可得
由例2.5.1,例2.5.2可知,若X的分布已知,Y=g(X),且Y为离散
量时,可先列出Y的可能取值…然后找出事件
的等价事件 ,从而求出Y的
分布律 即
可。另外,当Y=g(X)为连续量时,我们总是先找出{Y≤y},即
{g(X)≤y}的等价事件 ,从而求出Y的分布函数。总之,求随机变量函数的分布问题实质上就是找等价事件问题。
例2.5.3 设随机变量X的概率密度为Y=X2
,求Y的概率分布函数 及密度函数。
解 由题意知,当i≤0时,。
当0
例2.5.4 设X的概率密度为。求Y与Z的
概率密度 。
解 设Y与Z的分布函数分别为。当y≤0时,显然有 。当y>0时,有
当t≤0时,显然有 。当t>0时,有
定理2.5.1 设X为一连续型随机变量,其概率密度为
,随机变量Y=g(X),若函数y=g(x)为一严格单调
增函数(或减函数),且可微。记y=g(x)的反函数为x=h(y)。
则Y的概率密度为
其中D为函数y=g(x)的值域。
证明 先设y=g(x)为一严格单调增函数,即g′(x)≥0,注意此
时的h′(y)≥0。而Y的分布函数为从而。
若y=g(x)为一严格单调减函数,即g′(x)≤0,此时并有h′(y)
≤0。故Y的分布函数为
从而。这样就证明了(2.5.1)式。
例2.5.5 随机变量
求Y
的概率密度。
解 记y=g(x)=ax+b,则其反函数为。满足定理2.5.1的条件,故有
即 。特别地当。也就是说一个正态量的线性函数仍为正态量;特别地,当
是标准正态量。
例2.5.6 设连续型随机变量X的分布函数为F(x),且当0<
F(x)<1时F(x)为严格单调函数,记Y=F(X),证明:Y服从区间
(0,1)上的均匀分布。
证明 由分布函数的性质知,0≤F(x)≤l,故Y的取值也属于区间
[0,1]。显然有,当y≤0时,。
当0
即
由 的表示式就知Y~
U(0,1),命题得证。思考题二
1.随机变量与实变量有什么区别?
2.取值充满一区间的量一定是连续量吗?
3.若随机变量X分布律为 ,则X的分布函数是
,对吗?
4.设随机变量X,Y的概率密度分别为
,则以下可作为概率密度的是( )
(A)
(B)
(C)
(D)
5.以下函数中能作为概率分布函数的是6.设 ,对任意的
的值仅与μ有关吗?仅与
σ有关吗?还是与μ,σ都有关?
7.若一元件寿命服从指数分布,由指数分布的无记忆性,是否可
认为这元件永远不会损坏?习题二
1.从1,2,3,4,5,6,7这7个数中随机抽取3个数(不放回抽
样),并将其从小到大排队,设排在中间的数为X,求X的概率分布
律。
2.某电脑小游戏要依次独立地过3关,如果过不了关就结束。并规
定过了第1,2关各得1分,过了第3关记为4分,第1关未过得0分。若设
一玩者每关通过的概率为20%。
(1)写出此人得分数X的概率分布律;
(2)求此人得分数大于2的概率;
(3)已知此人得分不低于2,求此人得4分的概率。
3.某人买一种数字型体育彩票,每一注号码中大奖的概率为10-7。
(1)若每期买1注,共买了n期,求没有中大奖的概率;
(2)若每期买10注(号码全不同),共买了n期,求没有中大奖的
概率。
4.某医院男婴的出生率为0.51,如果在该院随机找3名新生儿,求
(1)至少有1名男婴的概率;
(2)恰有1名男婴的概率;
(3)第1,第2名是男婴,第3名是女婴的概率;
(4)第1,第2名是男婴的概率。
5.一车辆从A地到B地要经过3个特殊地段,经过这3个地段时车辆
发生故障的概率分别为 。设其余地段车辆
不发生事故,且记X为从A地到B地发生的故障数,Y为首次发生故障时已通过的特殊地段数(如没有发生故障,则记Y=3)。试分别写出X,Y的概率分布律。
6.从一批不合格品率为p(0
果查到不合格品就停止检查,且最多查5件产品。设停止时已检查了X件
产品。
(1)求X的概率分布律;
(2)求P{X≤2.5}的值。
7.要诊断可疑病人是否患有某种罕见疾病,常邀请国内5名著名专
家会诊,当至少有3名专家认为其有病时就诊断其有病。设每位专家“有
病诊断为无病”的概率为10%,“无病诊断为有病”的概率为20%,且专
家诊断行为独立。可疑病人有病的概率为70%。
(1)求此人有病的条件下,诊断为有病的概率α及此人无病的条件
下诊断为无病的概率β;
(2)求诊断正确的概率;
(3)此人被诊断为有病的概率。
8.(接第7题)若已知恰有3名专家意见一致,求诊断正确的概
率。
9.某公交车站单位时间内候车人数服从参数为λ的泊松分布。
(1)若已知单位时间内至少有1人候车的概率为
,求单位时间内至少有2人候车的概率;
(2)若λ=3.2,已知我们班有一位同学在那里候车,求这车站就他
1人候车的概率。
10.设某手机在早上9:00至晚上9:00的任一长度为t(分)的时间区间内收到的短信数X服从参数为λt的泊松分布, ,且
与时间起点无关。
(1)求10:00至12:00期间恰好收到6条短信的概率;
(2)已知在10:00至12:00期间至少有5条短信的条件下,求在该
时段恰好收到6条短信的概率。
11.某大学定每年的5月份为教职工进行体检,根据以往的情况
知,通过体检发现 的被检者患有重大疾病。已知有3000人参
加今年的体检,求至少有2人被检出重大疾病的概率(可用泊松分布近
似计算)。
12.设随机变量X具有以下性质:
(1)试写出X的概率分布函数;
(2)求P{X≤2.5}的值。
13.设随机变量X的概率密度为
(1)求常数c的值;
(2)求X的分布函数F(x);
(3)求P{-1
率。
14.已知在早上7:00~8:00有两班车(7:30,7:50)从A校区
到B校区,一学生在7:20~7:45随机到达车站乘这两辆车。
(1)求该学生等车时间小于10分钟的概率;
(2)该学生等车时间大于5分钟又小于15分钟的概率;
(3)已知其候车时间大于5分钟的条件下,求其乘上7:30的班车
的概率。
15.从区间(-1,3)中随机取一数X,试写出X的概率密度函
数;若在该区间随机取n个数,设其中有Y个数大于0,求P{Y=k},k
=0,1,2,…,n的值。
16.设随机变量X服从 ,其中μ=5,σ=1。求:
17.设A君的年收入扣除日常必需的花费后的余额(以万元计)X
服从N(2.3,0.25),且往年没有积蓄,也不打算借贷,今年他计划至
少花3万元买些中高档家电,你说他能实现自己计划的概率有多大?
18.设一地区的青年男子身高(以cm计)X服从N(170,5.02)。
今在这地区随机找一青年男子测身高。求:
(1)身高大于170cm的概率;
(2)身高大于165cm且小于175cm的概率;
(3)身高小于172cm的概率。
19.设系统电压小于200伏,在区间[200,240]伏和超过240伏3
种情况下,系统中某种电子元件不能正常工作的概率分别为0.1,0.001,0.2。设系统电压X服从N(220,252)。(1)求该电子元件不能正常工作的概率α;
(2)该电子元件不能正常工作时,求系统电压超过240伏的概率
β;
(3)若一系统有3个这种元件,且若至少有2只正常时系统运行正
常,求该系统运行正常的概率θ。
20.设随机变量Z服从标准正态分布,对于实数:x0
,若
,则称x0
为标准正态分布的上侧α分
位点,常记 。试用上侧分位点表示满足以下条
件的常数a,b,c,。
21.设随机变量X服从N(15,4),X落在区间
中的概率之比为50:34:16,求 的值。
22.设随机变量X的概率密度为。试求:
(1)常数a的值;(2) 的值。
23.设银行的某一柜台一位顾客的服务时间(以分计)服从参数λ
=18的指数分布,在A到达时恰好有1人先于其到达,设A的等待时间
为X。
(1)写出X的概率密度;
(2)求A等待时间超过10分钟的概率;
(3)求等待时间大于8分钟且小于16分钟的概率。
24.设甲,乙两厂生产的同类型产品寿命(以年计)分别服从参数
为13和16的指数分布,将两厂的产品混在一起,其中甲厂的产品数占
40%。现从这批混合产品中随机取一件产品。
(1)求该产品寿命大于6年的概率;
(2)若已知该产品使用了6年仍未坏,求该产品再使用2年不坏的
概率。
25.以X表示某商店早晨开门后直到第一个顾客到达的等待时间
(以分计),X的概率分布函数为
(1)求X的概率密度函数f(x);
(2)求P{5
(3)求某一周(7天)至少有6天等待时间不超过5分钟的概率。
26.设一批电子元件寿命X(以小时计)的概率密度函数为某人买了3只元件试用。若至少有2只寿命大于150小时,则下次再
买此类元件。求
(1)这3只元件中恰好有2只寿命大于150小时的概率;
(2)这个人会再买的概率。
27.某次游戏向每个玩者发5个球,向目标投掷,投中2次就结束投
球。若每次投中的概率均为p=0.7,且每次投掷是相互独立的。设X为
结束时的投球次数,规定当X=2时得10分,X=3时得8分,X≥4时得2
分,记Y为得分数。试写出Y的概率分布律。
28.已知随机变量X的概率密度函数为
(1)求常数c的值;
(2)设Y=3X,求Y的概率密度;
(3)设Z=|X|,求Z的概率分布函数及概率密度。
29.设在(0,t]时间区间内进入某商店的顾客数N(t)服从参数
为λt的泊松分布,且设先后两个顾客进入的间隔时间为T,(l)求T的概
率分布函数。(2)求
的值,其中 。
30.从区间(0,1)上随机取一数X,记
为自然数),求Y的概率密度。31.设随机变量X服从在 上的均匀分布,Y=
cosX,求Y的概率分布函数。
32.设随机变量
的概率密度。
33.设随机变量X的概率密度为
已知P{X
(1)求常数a,b; (2)设 ,求Y的概率密度
函数 。
34.设随机变量。(1)求Y的概率密度;(2)求Z的概率密度。第三章 多元随机变量及其分布
在第二章中,我们研究了单个随机变量的概率分布问题,但许多随
机现象用一个变量来描述是不够的,例如要预报明天的天气状况,就要
观察与预测许多个随机变量(如:温度、湿度、风力,等等)的变化情
况,又比如要制定一地区成年男子衬衣(大、中、小号的尺寸)标准,就需要研究这些人的衣长、袖长、领围、肩宽、胸围,等等随机变量以
及这些量之间的关系。所以研究多元随机变量是必需的。本教材将较深
入地研究二元随机变量,可能时可以将这些方法用于研究多元随机变
量。
设一随机试验E,其样本空间为S={e),定义随机变量X=
X(e),Y=Y(e),称向量(X,Y)为二元随机向量或称二元随机变
量。§3.1 二元离散型随机变量
定义3.1.1 若二元随机变量(X,Y)的取值有限或可列,则称
(X,Y)为二元离散型随机变量或称二元离散量。
(一)二元离散量的联合分布
设二元离散量(X,Y)的可能取值为
,与一元离散量相
似,称
为(X,Y)的联合概率分布律或简称联合分布律。上式亦可用列表的
方式表示。
联合分布律满足。
由概率的性质知(1)成立,又
是样本点,所以两两不相容,且其全体构成一样本空间,故(2)亦成
立。
例3.1.1 一袋中有5个白球,1个红球和2个黑球。每次摸1球,不放
回抽样3次。设3次中有X次摸到白球,Y次摸到红球,求(X,Y)的联
合概率分布律。
解 由题意知,X的可能取值为0,1,2,3,Y的可能取值为0,1。记 ,则
(下式中 即为组合数 )
(二)二元离散量的边际分布
设二元离散量(X,Y)的联合分布律为
,故有
同样可得
注:符号“ ”表示“记为”。
显然有,,即(3.1.2)及(3.1.3)满足分布律的性质,它们分别是随机变量X与Y
的概率分布律,分别称为关于X及关于Y的边际分布律或边缘分布律。
用列表的方法来表示联合及边际分布更能理解其字面的意义。
上表内第i行(或第j列)累计后记作 ,上表列
在联合分布律表的边上的这一列(或一行)恰是X(或Y)的分布律,故
称其为边际分布律。
例3.1.2 设一群体80%人不吸烟,有15%的人少量吸烟,5%的人
吸烟较多,且已知近期他们患呼吸道疾病(以下简称患病)的概率分别
为5%,25%,70%。记求:(1)(X,Y)的联合分布与边际分布;(2)求患病人中吸烟的概
率。
解 (1)记。由题意知,X的边际分布律为
(2)要求的概率为
即患病的人中有近65%的人吸烟。
(三)二元离散量的条件分布
从上面的例3.1.2(2)可以看到,研究二元离散量的条件概率是有趣和必要的。下面我们就来研究一下二元离散量的条件分布问题。
设二元离散量(X,Y)的联合分布律为
,则当 时,同理可得,当 时,称(3.1.4)(或(3.1.5))式为给定
的条件下X(或Y)的
条件分布律。
(3.1.4)式中显然有。同样,(3.1.5)式中有。亦即(3.1.4)及(3.1.5)式满足分布律的
性质。例3.1.3 设二元离散量(X,Y)的联合概率分布律为
且已知 求:
(1)a,b的值;(2){X=2}的条件下Y的条件分布律;(3){X
+Y=2}的条件下X的条件分布律。
解 (1)。由联合分布律的性质知,a+b+0.6=1,得b=0.4。
(2)P{X=2}=0.1+0.1+b=0.6。那么{X=2}的条件下Y的条
件分布律为
也可以写为(3)P{X+Y=2}=P{X=2,Y=0}+P{X=1,Y=1}=
0.3,那么
例3.1.4 设一单位送客车上车人数X服从参数为λ的泊松分布,每个
人行动独立,每个上车人在中途下车(没有坐到终点站)的概率为p,0
合分布律,X与Y的边际分布律以及条件分布律。
解 已知。且由题意知,当m=0,1,2,…时,即 。例3.1.5 一种叫“排列3”的彩票:每次从0~9这10个数中随机取一
个数,共取3次,得3个数的一个排列作为一期彩票的大奖号码。王先生
每一期去买10个不同排列的号码。设X为他首次中大奖时已买的彩票期
数,Y表示第2次中大奖已买彩票的期数。(1)求(X,Y)的联合分布
律;(2)已知他买了100期时第2次中大奖,求X的条件分布律。
解 (1)由题意知,每一个号码中大奖的概率为1103。买10个不
同号码,中大奖的概率为1100。记p=1100。
设Ai
={王先生买了第i期彩票中大奖},i=1,2,…则
即当已知王先生在买了100期彩票时第2次中大奖,则第1次中大奖在前
99期中是等可能的。§3.2 二元随机变量的分布函数
在§3.1中我们研究了二元离散型随机变量的联合分布律,边际分布
律与条件分布律。对二元随机变量的分布函数,我们同样要研究这三方
面的内容。
(一)二元随机变量的联合分布函数
定义3.2.1 设二元随机变量(X,Y),对于任意的实数x,y,称函
数
图3.2.1
为(X,Y)的联合分布函数。
若将(x,y)看作随机点的坐标,则分布函数F(x,y)即为(x,y)落在图3.2.1阴影部分区域的概率。
与一元随机变量的分布函数一样,相应地,F(x,y)具有以下性
质:
(1)当给定 关于y单调不减;当给定 关于x单调
不减。
(2)。
(3)
关于x右连续,关于y右连续。(证略)
(4)当实数 时,性质(1),(2)可参照一元变量的分布函数相应性质的证明方法
进行证明。
为了证明性质(4),设。易知。从而(二)二元随机变量的边际(边缘)分布函数
在§3.1中我们称单个变量的概率分布律为边际分布律,在此我们同
样称单个随机变量的分布函数为边际分布函数。
记二元变量(X,Y)的联合分布函数为F(x,y),X,Y的边际分
布函数为 ,则
同理, 。即,二元随
机变量的边际分布函数是联合分布函数当另一个变量趋向于+∞时的极
限函数。
以后我们不一一说明地常用 表
示X,Y的边际分布函数,用F(x,y)表示(X,Y)的联合分布函数。
(三)条件分布函数
设(x,y)为二元离散量,当
时,称函数
为 条件下Y的条件分布函数。
设(X,Y)为二元连续量(下一节介绍),当任意固定
时,称函数为{X=x}条件下Y的条件分布函数。
条件分布函数具有分布函数的所有性质。
例3.2.1 一袋中有a个白球,b个红球,记a+b=n。每次从袋中任
取一球,不放回抽样,设
(1)试写出 的联合分布函数
的边际分布函数
写出
当 的条件分布函数 。
解 记。由第一
章的例1.3.2,可知。
当,因此
于是可得 的联合分布律如下:(记N
=n(n-1))
那么 的联合分布函数F(x,y)为
(2) 有两种求法。方法一,由 的边际分布律求 ;方法二,可由。现采用方法二。
(3)由 的联合分布律可知,在
的条件下, 的条件分布律为
所以所要求的条件分布函数为§3.1 二元连续型随机变量
(一)二元连续量的联合分布
定义3.3.1 设(X,Y)为二元随机变量,若存在二元函数f(x,y)≥0,对任意的二维空间的集合D,有
则称(X,Y)为二元连续型随机变量,简称二元连续量。称f(x,y)
为(X,Y)的联合概率密度,简称联合密度。
f(x,y)具有以下性质:(其中F(x,y)为(X,Y)的联合分布
函数)
(4)在f(x,y)的连续点上有
由连续量的定义可知,二元连续量(X,Y)落在一面积测度为零的
区域上的概率为零,特别地落在一条曲线上的概率为零。
由f(x,y)的性质(4)知,在f(x,y)的连续点处有这表明(X,Y)的联合密度为(X,Y)落入矩形区域
的概率
与该区域面积之比,当 时的极限值,这与
物理量质量面密度是相通的。且当 充分小时,可得
即(X,Y)落在矩形区域D上的概率近似等于
,同时也表明f(x,y)是描述二元
变量(X,Y)落在点(x,y)附近的概率大小的一个量。
例3.3.1 设二元随机变量(X,Y)的联合概率密度为
其中。(1)求常数c;(2)求(X,Y)的联合分布函数;(3)求。
解 (1)由联合概率密度性质(3)可知
得c=15。
图3.3.1
(2)
,那么显然当x≤0或y≤0时,F(x,y)=0;当x≥1且y≥1时,F(x,y)
=1。
图3.3.2
当 (如图3.3.2)时,
图3.3.3
当 (如图3.3.3)时,同理可得,当0x时,即
(3)记
,则
亦可,(二)二元连续量的边际分布设(X,Y)为二元连续量,F(x,y),f(x,y)分别为(X,Y)
的联合分布函数及联合密度函数,称单个随机变量X(或Y)的密度函数
为X(或Y的边际密度函数,且常分别用
表示。由于
那么由连续型随机变量的定义知,X为连续量,且X的概率密度函数为
即边际密度为联合密度关于另一个变量在(-∞,+∞)上的积分。
例3.3.2 设二元随机变量(X,Y)的联合概率密度为
(1)求P{X+Y≥1}的值;(2)求X的边际密度 ;
(3)求P{X>l4}的值。
解 (1)由题意得,(2)当 时,当 。
(3)由题意得,(三)二元连续量的条件分布
图3.3.4
设(X,Y)为二元连续量,由条件分布函数的定义知,在一定的条件下,,且
因此我们有下面的定义:
定义3.3.2 设(X,Y)为二元连续量,f(x,y)为(X,Y)的联
合密度函数, 为X,Y的边际密度函
数。给定{X=x}的条件下,Y的条件密度函数为同样有
条件密度具有以下性质:(以 为例)
(4)给定x,当 在y处连续时,以后,我们不一一说明地常用f(x,y)表示(X,Y)的联合密
度,用 分别表示X,Y的边际密度。
例3.3.3 设有一件事需甲,乙两人先后接力完成,完成时间要求不
能超过30分钟。先由甲工作,再由乙接着干。设甲干了X(分钟),甲,乙两人共干了Y分钟,且设X服从(0,30)的均匀分布,Y服从
(X,30)的均匀分布。(1)求(X,Y)的联合密度;(2)求条件密
度 ;(3)当已知花了25分钟完成此事,求甲干
的时间不超过10分钟的概率。
解 由题意知,X~U(0,30),即由题意知,当甲干了x分钟结束时,Y服从(x,30)的均匀分布,故有,当0
30时,由(3.3.4)知,(2)由于
,所以当0
因此,当0
下面介绍两个重要的连续量。
定义3.3.3 设二元随机变量(X,Y)在二维有界区域D上取值,且
具有联合概率密度
则称(X,Y)服从D上均匀分布。
若D1
是D的一个子集,则可得到
定义3.3.4 设二元随机变量(X,Y)具有联合概率密度(式中其中
,则称(X,Y)服从参数为 的二元
正态分布,记为。
例3.3.4 设二元随机变量(X,Y)在
上均匀分布。(1)求关于X,Y的边际密度;(2)求给定X=x(0
条件下Y的条件密度;(3)求P{Y≤X}的值。
解 (1)因为(X,Y)在D上均勾分布,故(X,Y)具有联合密
度为
又 ,那么显
然,当x≤0或x≥1时,时,即
(2)当0
图3.3.5
(3)由图3.3.5知,,其中。D1
的面积 ,D的面积 ,故。
例3.3.5 设二元随机变量(X,Y)服从
分布。(1)求关于X,Y的边际
密度 ;(2)求条件密度。
解 (1)记 ,则
作积分变量变换,令
,则即 。同理可得。
(2)根据条件密度的定义,知
同理可得
即当 时,X,Y的
边际分布也是正态分布,。当给定X
=x的条件下,Y的条件分布亦为正态分布,此时Y服从。当给定Y
=y时,X的条件分布为。§3.4 随机变量的独立性
先回忆一下,在第一章中,两随机事件A,B独立的定义:当
时,称A,B相互独立。对于两个随机变量X,Y,有下面定义:
定义3.4.1对于任意两个实数集合 ,有
则称随机变量X,Y相互独立,简称X,Y独立。
利用概率的三条公理可知,当且仅当对任意实数x,y,有
即为 时
X,Y相互独立。 (3.4.2)
也就是说“对于任意的实数(x,y),(X,Y)的联合分布函数
F(x,y)都等于X与Y的边际分布函数
的乘积”可以作为变量x与Y独立的
等价定义。
特别地,当(X,Y)为二元离散量时,设X,Y的可能取值为
,X与Y相互独立的定
义等价于:对于任意的实数 ,都有当(X,Y)为二元连续量时,由(3.4.2)式得,对于任意的实数
x,y,有
由微积分知识知,两边积分处处相等,被积函数不一定要处处相等,即
可以在面积为零的区域不相等。也就是说,被积函数除了面积为零的区
域外处处相等,这种相等,我们称为几乎处处相等,即
几乎处处成立为连续量X,Y相互独立的等价定义。
当(X,Y)为二元离散量时,由(3.4.3)知,若存在
使得
,则X与Y不独立;当
(X,Y)为二元连续量时,若存在一个面积不为零的区域D0
,使得
,则X与Y亦不独立。
由(3.4.1)式可知,对任意集合
时,X,Y独立的定义亦可写成
由独立的定义知,§3.1的例3.1.2中X与Y不独立。因为
也就是吸烟的多少与患呼吸道疾病是有关的,不独立的。再如§3.3的例3.3.4中的X,Y亦不独立,因为当0
特别地,若(X,Y)为二元正态量,由本章§3.3例3.3.5知,X与Y相
互独立的充分必要条件为ρ=0。因为当且仅当ρ=0时,(3.4.4)式成
立。
在实际问题中,当一个变量的取值不影响另一个变量取任何值的概
率时,常认为这两个变量独立。
图3.4.1
例3.4.1 设在a地与B地间的距离(以公里计)为l(l>1)的公路上
有一辆急修车,急修车所在的位置是随机的。行使中的车辆抛锚地点也
是随机的。求急修车与抛锚车的距离小于0.5公里的概率。
解 设急修车离A地的距离为X,抛锚车离A地的距离为Y。由题意
知,x与y独立,且均在(0,l)上均勾分布。所要求的概率为
定理3.4.1 二元连续量X,Y相互独立的充要条件是X,Y的联合密
度f(x,y)几乎处处可写成x的函数m(x)与y的函数n(y)的乘积,即证明 先证必要性。当X,Y独立时,由(3.4.4)式知,下式几乎
处处成立
记。
再证充分性。当
时,由密度函
数的性质知
记
,那么ab=1。再结合边际密度与联合密度函数的关系,可得
同理得, 。所以
那么由(3.4.4)式知X,Y相互独立。
例3.4.2 问在下面两种情况下,X与Y独立吗?
(1)设(X,Y)的联合密度为(2)设(X,Y)的联合密度为
解 (1)记
故X,Y独立。
(2)由于f(x,y)不能分解成x的函数与y的函数的乘积,故X,Y
不独立。从另一角度来看,我们可以求得X,Y的边际密度分别为
故当。那么由(3.4.4)知,也可知X,Y不独立。
以上关于二元随机变量的一些概念,容易推广到n元随机变量的情
形。
例如:联合分布函数的概念,n元随机变量的联合分布函数为
其中 为任意的实数。
关于边际分布函数,以下举例说明,其他情形可举一反三。例如:
当n>2时,有 的联合边际分布函数
类似地,也可以定义n元离散量与n元连续量。当
的取值至多可列时,称
为n元离散量;若对任意n维
空间的集合D,存在非负函数
,使得
成立,则称 为n元的
连续型随机变量,简称n元连续量,其中的
称之为
的联合概率密度。关于边际概率密度,类似地有,例如:
等等。
若对于任意的实数集 ,有
则称 相互独立。
也即对任意的实数
,有
则称 相互独立。
当 为n元离散量时,亦有如
(3.4.3)类似的独立的等价定义,当
为n元连续量时,亦有如(3.4.4)式相类似的独立的等
价定义。定义3.4.2 设
分别为m元,n元的随机变量,分别用
记它们的联合分布函数。再记
的联合分布函数。
对任意的实数
,若有
则称两向量组
相互独立。
例3.4.3 在n次独立重复的试验中,设每次试验有4个结果:。且每次试验 发生的概率不
变。设。再设在n次试验中 发生的值;(2)在给定 的条件下求
的条件分布律;(3)在给定
的条件下求 的条件
分布律。
解 (1)与n重贝努里试验及二项分布的讨论一样,可知事件
共有n!(n1!n2!n3!n4!)种方式数。而每个Ai
在确定的ni
次发生的概
率为 ,故有
(2)由题知
上面运算用到等式
所以 。故当n1
=0,1,…,n时,(3)先求(X1
,X2)的边际分布
那么当 时,即当给定 的条件下,X3
的
条件分布为。
例3.4.4 一咨询台有A,B两个窗口,设每个顾客服务时间服从参
数为λ的指数分布。有一天一开门,A窗口有一个人要求服务。B窗口有
两人排队要求服务,设每人服务时间相互独立,求B窗口两人先于A窗口1人结束服务的概率。
解 设A窗口一人的服务时间为X1
,B窗口的两个人的服务时间分别
为X2
,X3
,由题意知,X1
,X2
,X3
相互独立。所要求的概率即为
其中, 的联合密度,由题意知,§3.5 二元随机变量函数的分布
在第二章的§2.5中我们研究了一元随机变量的函数的分布问题,并
提到了求一元随机变量函数的分布问题实质是找等价事件。其实求二元
随机变量函数的分布问题实质上也是寻找等价事件。当然求二元随机变
量函数的分布问题较为复杂,下面我们将对一些特殊的形式进行详细的
讨论。
(一)Z=X+Y的分布
在这一部分中,我们将研究已知二元随机变量(X,Y)的概率分
布,求Z=X+Y的概率分布问题。
若(X,Y)为二元离散量,设
,设Z的可能取值为z1
,z2
,…,zk
,…,则显然有
特别地,当X与Y相互独立时,(3.5.1)与(3.5.2)式就可写成
若(X,Y)为二元连续量,设(X,Y)的联合密度为f(x,y),则Z的概率分布函数为作积分变量变换
图3.4.2
这样的变换下可知dxdy=dudv,所以
从而,若作的积分变换为 ,通过同样的计算可得
特别地,当X,Y相互独立时,(3.5.5)式与(3.5.6)式就可写成
例3.5.1 设X~π(λ1),Y~π(λ2),X,Y相互独立。若Z=X+Y,求Z的概率分布律。
解 由题意知,即Z~π(λ1
+λ2)。也就是说,两个独立的泊松分布的随机变量的和仍
服从泊松分布,其参数为两个随机变量的参数之和。
用数学归纳法可以证明:n个独立的服从泊松分布的随机变量的和
仍服从泊松分布,其参数为n个变量的参数之和。
例3.5.2 设
,X,Y独立,Z=X+Y,求Z的概率密度。
对上式积分作积分变量变换,令u=x-t(l+σ2),可知du=dx,从而
可知,此积分值为与t无关的常数,暂且记作a,得
有上式可知 。若当
,X,Y独立时,由例2.5.5知
,由例3.5.2知
再由例2.5.5可得。
用数学归纳法可证,n个独立的正态量之和仍为正态量。
即若,X1
,X2
,…,Xn
独立,且。
进一步可以证明:n个独立的正态量的线性组合仍为正态量。
例3.5.3 设某服务台顾客等待时间(以分计)X服从参数为λ的指数分布,接受服务的时间Y服从(0,20)上的均匀分布,且设X,Y独
立。记顾客在服务台的总时间为Z,即Z=X+Y。(1)求Z的概率密度
函数fZ
(t);(2)设λ=l20,求总时间不超过45分钟的概率。
解 由题意知,因为X,Y独立,所以X,Y的联合概率密度为
方法一:利用(3.5.5)式,
图3.5.1由图3.5.1知,当t≤0时,FZ
(t)=0;
当0
当t≥20时,。
图3.5.2
方法二:可先求Z的分布函数,再求FZ
(t)。由于FZ
(t)=P{X
+Y≤t},由图3.5.2知,当t≤0时FZ
(t)=0。
当0
(2)方法一:利用(1)中的方法二求出FZ
(t)可知,当λ=l20
时,方法二:可由Z的密度函数来计算得到:
例3.5.4 设二元随机变量(X,Y)的联合概率密度为
图3.5.3解 由(3.5.5)式可知
,而且
由(X,Y)的联合概率密度及定理3.4.1知,X,Y不独立,且
显然,当t≤0或t≥2时,fZ
(t)=0;
例3.5.5 某人一天做两份工作,一份工作得到的酬金X具有概率分
布律 ,另一份工作的酬金Y服从N(15,4)。设X,Y独立,记一天酬金总数为Z,Z=X+Y。(1)求Z的概率密
度;(2)求一天酬金多于30的概率。
解 (1)先求Z的概率分布函数,利用全概率公式
因为X与Y独立,故有(2)我们有
(二)M=max(X,Y),N=min(X,Y)的分布
记X,Y的联合分布函数为F(x,y),且记FX
(t),FY
(t)分别
为X,Y的分布函数。
先来讨论M的分布函数,由M的定义可知
特别地,当X与Y独立时,再讨论N的分布函数
特别地,当X与Y独立时,以上结果容易推广到n个变量的情形。特别地,设X1
,X2
,…,Xn
为n个
相互独立的随机变量,相应的分布函数分别为F1
(x1),F2(x2),…,Fn
(xn),记M=max(X1
,X2
,…,Xn),N=min(X1
,X2
,…,Xn),则有例3.5.6 一批元件的寿命服从参数为λ的指数分布,从中随机地取4
件,其寿命记为X1
,X2
,X3
,X4
,由于是随机抽取,故这4个元件的寿命
相互独立。记。(1)求N,M的概率分布函数及概率密度函
数;(2)将4个元件如图连接成一系统,求系统寿命大于t0
(t0
>0)的
概率。
图3.5.4
解 (1)由于X1
,X2
,X3
,X4
相互独立且均服从参数为λ的指数分
布,故当t>0时,(2)设系统寿命为T,则T=min[max(X1
,X2),X3
,X4
],那么
对t0
>而言,有思考题三
1.若已知二元随机变量(X,Y)的联合概率分布就决定了X及Y的
边际概率分布;反之,若已知X及Y的边际概率分布就可决定(X,Y)
的联合概率分布,对吗?若不对,请给出正确的说法。
2.设随机变量X与Y同分布,则以下说法正确吗?
(1)P{X=Y}=l;
(2)P{X+Y=2X}=1;
(3)X与Y有相同的概率分布函数;
(4)X与Y可以有不同的概率分布函数。
3.设二元连续量(X,Y)的联合概率密度为
则(X,Y)的联合分布函数为
对吗?
4.设(X,Y)为二元连续量,则以下等式正确吗?(1) ;
(2) ;
(3);
(4)。
5.当(X,Y)为二元离散量时,若存在点(x0
,y0)使
,则X与Y不独立,对吗?当(X,Y)为二元连续量时,若存在一点
(x0
,y0)使
,则X与Y不独立,对吗?习题三
1.有两个口袋均放着3个红球,2个白球,今从两口袋中同时摸出1
球互换(设每个口袋摸到每个球的概率相等)。记X,Y分别为两袋中互
换球后的红球数,求(X,Y)的联合分布律及关于X的边际分布律。
2.设二元随机变量(X,Y)的联合概率分布律为
且已知事件{X=0}与事件{X+Y=1}相互独立,求常数a,b的值。
3.设二元随机变量(X,Y)的联合概率分布律为
已知P{Y≤0|X<2}=0.5,及P{Y=l}=0.5,求a,b,c的值及X,Y
的边际分布律。4.设随机变量X,Y的概率分布律分别为且已知P{X=0,Y=0}=P{X=1,Y=1}=0.1。
(1)试写出(X,Y)的联合概率分布律;
(2)写出在{X=0}的条件下Y的条件分布律。
5.将一枚均匀的硬币抛3次,记X为3次中正面的次数,Y为3次中正
面次数与反面次数之差的绝对值。
(1)求(X,Y)的联合分布律及边际分布律;
(2)写出{Y=l}的条件下X的条件分布律。
6.某公司出钱为职工订报,每位职工可以从A,B,C3份报中任订
一份,已知有23的女职工决定订A报,有35的男职工决定订B报,余下
的人在3份报中随机选一份。公司男、女职工各占一半。从该公司中随
机找一职工,记
(1)试写出(X,Y)的联合概率分布律;
(2)求Y的边际分布律;
(3)求{Y=l}的条件下,X的条件分布律。
7.设某路段单位时间内发生的交通事故数X服从参数为λ的泊松分
布,其中因超速引起的占总事故数的10%。设因超速引发的事故数
为Y。
(1)求(X,Y)的联合分布律;
(2)求Y的边际分布律。
8.设一大型设备单位时间内发生的故障数X具有概率分布律每次故障以概率p带来损失a(万元)。设Y为该设备在单位时间内的损
失(以万元计)。
(1)求(X,Y)的联合分布律;
(2)已知发生了1次故障,求Y的条件分布律。
9.已知二元随机变量(X,Y)的联合分布函数为
(1)求(X,Y)的边际分布函数FX
(x),FY
(y);
(2)求关于X,Y的边际分布律;
(3)求(X,Y)的联合分布律。
10.设A,B为两随机事件,已知。引入随机变量X,Y,分别为
(1)求(X,Y)的联合分布律;(2)求(X,Y)的联合分布函数;
11.在第10题中,若已知{X=l}的条件下求Y的条件分布函数。
12.设(X,Y)为二元随机变量,已知P{X=0,Y=0}=P{X=
l,Y=l}=0.1,且知(X,Y)落在D={(x,y):0
1}的任一小区域内的概率与该小区域面积成正比,求(X,Y)的联合
分布函数。
13.设二元随机变量(X,Y)的联合概率密度为
(1)求常数c;
(2)求P{X+Y≤1}的值;
(3)求P{X<0.5}的值。
14.二元随机变量(X,Y)的联合概率密度为
(1)求常数c的值;
(2)求X,Y的边际概率密度fX
(x),FY
(y)。
15.二元随机变量(X,Y)的联合概率密度为
(1)求的边际概率密度fX
(x),FY
(y);
(2)求条件概率密度函数fY|X
(y|x);(3)当已知{X=x}时,问Y的条件分布是均匀分布吗?为什么?
16.设(X,Y)为二元随机变量,X的概率密度为
其中λ>0。当:x>0时,Y的条件密度为
(1)求(X,Y)的联合概率密度;
(2)求当x>0时,在给定{X=x}的条件下Y的条件分布函数;
(3)求P{Y>1|X=1}的值。
17.设二元随机变量(X,Y)的联合概率密度为
(1)求Y的边际概率密度fY
(y);
(2)求条件概率密度函数fX|Y
(x|y);
(3)计算 的值。
18.在区间(0,1)上随机取一数X,再在区间(X,l)上随机取
一数Y。(1)求(X,Y)的联合概率密度;
(2)求已知{Y=y}(0
19.在A地至B地(长为m公里)的公路上,事故发生地在离A地X公
里处,事故处理车在离A地Y公里处,X与Y均服从(0,m)上均匀分
布,且设X与Y独立。求事故车与处理车的距离Z的概率密度函教。
20.在半圆
内随机投点A,设A点的坐标为(X,Y)。
(1)求Y的边际密度fY
(y);
(2)求P{Y
(3)X与Y独立吗?为什么?
21.设二元随机变量(X,Y)服从。
(1)试写X,Y的边际概率密度;
(2)写出在{X=0}的条件下Y的条件概率密度;
(3)求P{Y≤1|X=0}的值。
22.设二元随机变量(X,Y)的联合概率密度为
其中f1
(x,y)与f2
(x,y)分别为二元正态变量(X1
,Y1)与(X2
,Y2)的概率密度,且已知(Xi
,Yi)(i=1,2)的边际分布均为标准正态分
布。
(1)求X,Y的边际概率密度fX
(x),fY
(y);
(2)问当(Xi
,Yi)的分布中的参数ρi
=0(i=1,2)时,X与Y独
立吗?
23.一设备由3个独立工作的子系统组成,若其中至少有2个子系统
正常工作时设备就能正常工作。各系统正常工作时间记为X1
,X2
,X3
,且均服从参数为λ的指数分布。求该设备正常工作时间的概率分布函数
及概率密度函数。
24.(1)设随机变量X1
,X2
,…,Xn
独立且均服从参数为p(0
<1)的0-1分布,记 ,求Z的概率分布律。
(2)设X~B(m,p),Y~B(n,p),X与Y相互独立。记W=X
+Y,求W的概率分布律。
25.设随机变量X在区间(-a,a)均匀分布,其中
,X与Y独立,Z=X+Y,求Z的
概率密度。
26.设二元随机变量(X,Y)的联合概率密度为
若Z=X+Y,求Z的概率密度。
27.设有一煤矿一天的产煤量X(以万吨计)服从N(l.5,0.12)分
布。设每天产量相互独立,一个月按30天计,求一月总产量超46万吨的
概率。28.某人连续参加2场比赛,第1,2场比赛可得的奖金数分别为X,Y,且已知 ,Y具有概率密度f(y),X与Y
相互独立。求此人奖金总数Z的概率密度。
29.设一本书一页的错误个数X服从参数为λ的泊松分布,且各页错
误数相互独立。现随机选10页,其错误数分别记为X1
,X2
,…,X10。
(1)求 的值;
(2)求 的值;
(3)求
的值;
30.设随机变量X,Y相互独立,且具有以下分布律
记Z=X+Y,M=max(X,Y),N=min(X,Y),分别求Z,M,N的概率分布律。
31.设一系统由2个独立的子系统组成,分别以X,Y记两个子系统的正常工作时间,且设X,Y分别服从参数为λ1
与λ2
的指数分布。当这2个
子系统分别(1)串联,(2)并联,(3)有备份(当一个损坏时另一
个接着工作)时,分别求系统正常工作时间T的概率密度函数。
32.设二元随机变量(X,Y)的联合概率密度为
记Z=2X-Y,求Z的概率密度。
33.设随机变量X与Y独立同分布,分布律均为。定义
(1)对X独立观察n次,求n次观察值之和W的概率分布律;
(2)求(X,Z)的联合概率分布律。
34.在区间(0,1)上随机取两数X,Y,记Z=XY,求Z的概率分
布函数及概率密度函数。第四章 随机变量的数字特征
在本章的开头,我们先来看一些来自我国官方的数据。
2010年7月16日,国家统计局发布的信息中有以下内容:2009年
(我国)城镇非私营单位在岗职工年平均工资为32736元(2008年为
29229元),城镇私营单位就业人员年均工资为18199元(2008年为
17071元);由上海市统计局发布的信息知,2009年上海城镇居民人均
住房建筑面积为34m2;由杭州市疾控中心发布的信息知,2009年杭州市
居民(大杭州范围,包括区县市)平均期望寿命为80.26岁(即按2009
年的死亡水平,预测2009年出生的孩子。平均可活80.26岁),其中男
性平均期望寿命为77.98岁,女性为82.76岁;国家统计局每个月公布的
居民消费价格指数——CPI(Consumer Price Index),工业品出厂价格
指数——PPI(Producer Price Index)等等。从报纸、电视、网络上我们
能够不断地得到各种各样的信息数据,这些数据是人们根据需要而定义
的。这些数据会影响政府的决策、投资的策略、股票期货市场的波动等
等,甚至引起全世界的关注。因为这些数据浓縮了许多信息,高度集中
地反映了当今社会的某一方面的特性。
从概率统计理论的角度看,职工工资、居民的住房面积、人的寿
命、居民的消费量、工业品出厂价格等都是随机变量,看来有时人们常
常会忽略其概率分布而重视一些能反映其特性的数据(指标量)。简单
地说,称那些能反映随机变量特性的量为随机变量的数字特征或特征
数。实际问题中常用样本数据来分析研究特征数(这要到后面的数理统
计部分讨论)。本章将介绍一元随机变量的数学期望、方差、变异系
数、分位数,以及多元随机变量的协方差、相关系数等常用数字特征。§4.1 数学期望
(一)数学期望的定义
随机变量的数学期望又称为平均数,在介绍其定义之前,我们先看
一个例子:
设抛一颗骰子所得的点数为X,独立重复地抛50次,若观察到为1,2,…,6点的次数分别为8,9,6,8,9,10次,则平均点数为
也就是说,平均值 是X的取值与相应事件的频率的乘积之和。
由§1.2节概率的统计定义知,频率的稳定值定义为概率。因此对于
离散型的随机变量我们有以下定义。
定义4.1.1 设离散型随机变量X的分布律为
若级数 绝对收敛(即),则称级数 为X的数学期望,记为E(X),即其中E是英文expectation的第一个字母。若
,则称随机变量X(等价地,相应的分布)的数学期望不存在。
数学期望的存在需要级数 绝对收敛,这是因为若该
级数不是绝对收敛,而仅仅是条件收敛,此时级数的和会随着级数各项
的排列次序不同而发生改变,从而无法得到唯一的和值。而从直观意义
上来看,离散型随机变量的平均值也应当与分布律中的各项排列次序无
关。
例4.1.1 一种常见的赌博游戏,抛一颗骰子,抛之前让赌客猜结果
为几点,凡猜中者以1:5得奖金,而且规定不管猜中与否押金均归庄家
所有,问此规则对谁有利。
解 不妨假设赌客每次押10元钱,设所得的奖金数为X,据规则他
得50元奖金的概率为16,血本无归的概率为56,因此他赌一次期望能
得到的奖金数为
因此这显然对庄家有利。(试想:否则赌场的开销与高额的利润从何而
来。)
从例4.1.1我们也可体会到“数学期望”这词的含义。
类似地,根据连续型随机变量的定义及积分与级数的关系,对于连
续型随机变量的数学期望可以给出如下定义:
定义4.1.2 设连续型随机变量X的密度函数为f(x)。若,则称积分
为X的数学期望,记为E(X),即
若 ,则称随机变
量X(等价地,相应的分布)的数学期望不存在。
例4.1.2 (泊松分布的数学期望)设随机变量X服从泊松分布
π(λ)(λ>0),则
这表明泊松分布中的参数λ恰好就是此分布的数学期望。那么若已
知泊松分布的期望,则该泊松分布就完全确定了。
例4.1.3 (指数分布的数学期望)设随机变量X服从指数分布
E(λ)(λ>0),则
即指数分布的数学期望为其参数λ的倒数,这也说明指数分布可由其数
学期望完全确定。例4.1.4 (标准正态分布的数学期望)设随机变量X服从标准正态
分布N(0,1),注意到标准正态分布的密度函数
是一偶函数,那么xφ(x)是一奇函数,故
一些重要的随机变量的特征数在书后附表1中能查到。
例4.1.5 某厂生产的电子产品,其寿命(单位:年)服从指数分
布,概率密度函数为
若每件产品的生产成本为350元,出售价格为500元。厂方向顾客承诺,如果售出1年之内发生故障,则免费调换一件,之后厂方不再承担后续
责任;如果在1年以上3年之内发生故障,则予以一次免费维修,维修成
本为50元,超过三年,则不负责维修。在这样的体系下,请问该厂每售
出一件产品,其平均净收入为多少?
解 记某件产品寿命为X,售出该产品的净收入为Y,则显然Y是X
的函数,由于X服从指数分布,那么因此售出一件产品的平均净收入为
例4.1.6 从区间[0,1]中随机地抽取n个数,记为Xi
,i=1,2,…,n,n≥1,记
,求E(M)与E(N)。
解 由题意知,Xi
,i=1,2,…,n是相互独立的随机变量,且均
服从U(0,1),其分布函数为
从而M的分布函数为那么M的概率密度函数为
而N的分布函数为
所以N的概率密度函数为
其中
为Beta函数,a>0,b>0。
关于随机变量期望的计算问题,还有以下定理。
定理4.1.1 若随机变量X的分布函数为F(x),则特别地,当X为非负随机变量(即P(X≥0)=1)时,有
当X为取非负整数值的随机变量时,有
证明略,因为证明需要用到带有斯蒂尔切斯积分的一般随机变量数
学期望的定义。
例4.1.7 设X服从(-1,2)上的均勾分布。令Y=max{X,0},求E(Y)。
解 由Y的定义知其分布函数为
可见,Y既不是离散量,也不是连续量。由于P{Y≥0}=1,利用
(4.1.4)式,可得
例4.1.8 设随机变量X的分布律为
是发散的,故该分布的数学期望不存在。下文中,如无特殊说明,总是假设所提到的随机变量的数学期望是
存在的。
(二)随机变量函数的数学期望
有时会碰到这样的情形:已知随机变量Y=g(X),其中随机变量
X的分布已知,需要得到Y的数学期望。一种自然的思路是先利用两者之
间的关系式及X的分布来求出Y的分布,然后再根据数学期望的定义来得
到Y的期望。这样当然是可行的,但是期望仅仅是随机变量的一个数字
特征,也就是一局部信息。为了得到部分信息,而要先得到其全部信
息,似乎有点“小题大作”之嫌。事实上,当两者之间的函数关系满足一
定条件时,确实不用这么麻烦。可以根据两个变量的关系表达式及已知
随机变量的分布,直接来求另一个随机变量的期望。下面就给出这一简
便公式。
定理4.1.2 当X为离散型随机变量时,若
,则g(X)的数学期
望E(g(X))存在,且
其中P(X=xi)=pi
,i=1,2,…为X的分布律。
当X为连续型随机变量时,若
,则g(X)的数学期望E(g(X))存在,且
其中f(x)为X的概率密度函数。证明 我们仅就X为离散型随机变量时给出证明。类似可证明连续
型随机变量情形。
记Y=g(X),由离散量取值的至多可列的性质可知,Y仍然是离
散量,其可能取值记为y1
,y2
,…,则
由假设知
所以E(Y)=E(g(X))存在,且
即为(4.1.6)式。
上述定理还可以推广到两个或两个以上随机变量函数的情形。
定理4.1.3 当(X,Y)为二元离散型随机变量时,若实函数h(x,y)满足
则h(X,Y)的数学期望E(h(X,Y))存在,且其中
的联合分布律。
当(X,Y)为二元连续型随机变量时,若实函数h(x,y)满足
则h(X,Y)的数学期望E(X,Y))存在,且
其中f(x,y)为(X,Y)的联合密度函数。
例4.1.9 某校区的门口设有电瓶校园游览车,每天早上7:00开始发
车,每隔15分钟一班。假设某人在早上9:00~10:00之间随机来到校门口
乘坐游览车,求此人等候游览车的平均时间。
解 由题意,设该游客在9点的第X分钟到达校门口乘坐游览车,则X服从[0,60]上的均匀分布。用Y表示该游客的等候时间,则根据游
览车的发车安排,有
所以例4.1.10 对于例4.1.7中的Y=max{X,0}的期望,也可以用随机
变量函数的期望来求。
解 由于X的密度函数为
取g(x)=max{x,0},则Y=g(X),利用(4.1.7)式,可得
例4.1.11 随机变量X,Y相互独立,均服从参数为 的0-1分
布,求:
解 由题意知,X与Y的联合分布律为
利用(4.1.8),可得同理可得
例4.1.12 设二元随机变量(X,Y)的联合概率密度为
求E(XY)。
解 利用定理4.1.3,可知
在数学期望的实际应用中,还常常涉及到极值的求解。
例4.1.13 设按季节出售的某种应时产品的销售量X(单位:吨)是
一个服从[5,10]上均匀分布的随机变量。若销售出一吨产品可盈利2
万元;但若在销售季节未能售完,造成积压,则每吨产品将会净亏损
0.5万元。若该厂家需要提前生产该种产品,为使厂家能获得最大的期
望利润,问:应在该季生产多少吨产品最为合适?
解 设该季应生产a吨产品(5≤a≤10),利润为Y万元,则Y依赖于销售量X及产量a,由于X服从[5,10]上的均匀分布,所以其概率密度函数为
所以该季平均利润为
为求使得该季平均利润达到最大的a,令
,所以当a=9时,E(Y)达到最大
值,即从能获得最大的期望利润角度出发,厂家应在该季生产9吨产品
最为合适。
(三)数学期望的性质
定理4.1.4 若n个随机变量,X1
,X2
,…,Xn
的期望都存在,则对任
意n+1个实数 ,的期望也存在,且
当n=l和n=2时可用定理4.1.2和4.1.3来证明,然后利用归纳法易得
上述结论。这里就不详细证明了。
特别地,当ci
=0,i=l,2,…,n时,得E(c0)=c0
,即对于任意
常数c,有
例4.1.14 (正态分布的数学期望)随机变量X服从正态分布
,所以任意正态分布的随机变量都可以写成标准正态分布随机变量的线
性组合,即X=σ·Z+μ,据例4.1.4知E(Z)=0,那么
这表明正态分布中的参数μ恰是此分布的数学期望。
例4.1.15 计算机程序随机地产生0~9中的数字。记Xi
为第i次产生的
数字,i=1,2,…,n。将这n个数依次排列(第一个产生的数字放在
个位,第二个产生的数字放在十位,…,依此类推),得到一数,记
为Y,求E(Y)。
解 由题意知,Xi
独立同分布i=l,2,…,n,其分布律均为故对任意的
,从而
例4.1.16 一民航机场大巴载有20位乘客从机场开出,沿途有10个
车站可以下车,如到达一个车站没有乘客下车就不停车,以X表示沿途
停车的次数,求该大巴平均停车次数(假设每位乘客下车与否是相互独
立的,并且在每个车站下车是等可能的)。
解 令
则显然 的分布律为
此题中将一个复杂的随机变量分解为若干个分布简单的易求数学期
望的随机变量之和,再利用期望的线性组合的性质使得问题迎刃而解。
这种处理方法具有一定的代表性。
例4.1.17 (二项分布的数学期望)设随机变量X服从二项分
布B(n,p)(0
独立且具有相同参数的0-1分布随机变量的和,即令Yi
表示服从参数同
为p的0-1分布的相互独立的随机变量,i=l,2,…,n,则
于是。
当然此结果也可以采用数学期望的定义得到(读者不妨自己计算一
下)。
注意:例4.1.16中的Xi
虽然服从参数相同的0-1分布,但是它们之
间不是相互独立的,因此 不服从二项分布。这一点请读者细
细体会,在以后的实际应用中要特别留意,加以区别。但是由定理
4.1.4,可知随机变量之和的期望是不依赖于和项中随机变量之间的关系
的。
例4.1.18 设有m个0与n个1随机地排成一个序列,m≥1,n≥1,假设
每种排列都是等可能的。在排列中,以0为界限的一串1或以1为界限的
一串0,称之为一个游程,即,连在一起的一串0构成“0”的一个游程,连在一起的一串1构成“1”的一个游程。例如,m=5,n=4,形成这样一
个排列:0,0,0,1,1,0,1,1,0,则这个序列中有3个“0”的游程
和2个“1”的游程。记R(i)为排列中“i”的游程的个数(i=0,1),求
各类游程的平均个数。
解 易知这样的?m+n个数的排列一共有(m+n)!(m!n!)种。令
那么 ,由于
当2≤i≤m+n时,所以
类似可得, 。这样序
列的总游程的均值为
定理4.1.5 n个相互独立随机变量的乘积的期望等于它们期望的乘
积。即若随机变量X1
,X2
,…,Xn
相互独立,期望都存在,则的期望也存在,且
证明 下面仅就n=2且(X1
,X2)是连续型的情形给出证明,其他
情形可以类似得到。设(X1
,X2)的联合密度函数是f(x,y),其边际
密度函数为fi
(x),i=1,2。由独立性,知f(x,y)=f1
(x)
·f2
(y)。此时利用定理4.1.3,有
故X1
X2
的期望存在,且再次利用定理4.1.3,有
例4.1.19 一长方形土地,其边长的测量值(单位:米)X,Y分别
服从N(150,32)和N(165,22),且X与Y相互独立,求土地面积W的
数学期望。
解 由题意知,W=XY,且X与Y相互独立,故
(四)条件数学期望
在§3.1、§3.2与§3.3中曾涉及到离散型和连续型随机变量的条件分
布,我们知道条件分布也是一种概率分布,因此也可以关于它求数学期
望,称为条件数学期望(conditional expenctation),简称为条件期
望,其具体定义如下:定义4.1.3 若(X,Y)为二维离散型随机变量,且在给定X=x
下,Y的条件分布律为;或者(X,Y)为二维连续型随机变量,在给定{X=x}下,Y的条件
概率密度函数为 ,则在给定了随机变量X取值
为x的条件下,Y的条件期望为
有时也简记为E(Y|x)。
期望所具有的性质,条件期望也同样满足。不过值得注意的是,条
件期望与期望还是有一些区别的。期望E(Y)是一个数值,而条件期
望E(Y|X=x)是x的函数。因此E(Y|X)是个随机变量,当观测到X
=x,时,其值为E(Y|X=x)。对于随机变量E(Y|X),还有以下
一个有趣的性质:
定理4.1.6 (X,Y)为二维随机变量,若存在,则
上式称为全(数学)期望公式(total expectation formula)。
特别地,当(X,Y)为二维离散型随机变量时,(4.1.13)就变成
了
其中xi
,i=l,2,…,为X的所有可能取值。
证明 我们就连续型随机变量与离散型随机变量分别进行证明。先
设(X,Y)为二维连续型随机变量,若其联合概率密度函数为f(x,y),记X与Y的边际概率密度函数分别为fX
(x)与fY
(y)。由条件期望定义知
其中 是在{X=x}条件
下Y的条件密度函数。由此可知E(Y|X)是X的函数,那么利用随机变
量函数的数学期望计算公式(4.1.7),得
若(X,Y)为二维离散型随机变量,若其联合分布律为pij
=P{X
=xi
,Y=yj
}(i,j=1,2,…)。同样利用条件期望的定义,(4.1.6)式以及条件概率定义,得
例4.1.20 设进入某超市的顾客购买一件该超市的自创品的概率
为p(00)的
泊松分布,求一天中该超市卖出其自创品的平均件数。
解 设一天中该超市卖出其自创品的数目为N件。由题意知,当顾
客流量X=i时,N的条件分布为B(i,p),因此对任意的i=0,l,…,有E(N|X=i)=ip。利用全期望公式,可得此题也可以参照例3.1.4,先求出N的分布律,可以得到N服从参数
为pλ的泊松分布,从而得E(N)=pλ。
例4.1.21 在某游戏迷宫的入口处,有编号为1,2,3,4的四个
门,每位游客可先从装有编号为1,2,3,4的4个号码中(等可能地)
随机取一号码,作为进入的门号,4个门中其中有一个是自由门(没有
固定的编号),选择此门,则5分钟后可以走出迷宫;剩下的三门分别
在走了10分,20分,30分钟后又重回人口处。重复前面的步骤,求他走
出迷宫所需的平均时间。
解 设游客走出迷宫所需时间为T分钟,并设他对门的选择情况
为X,用1,2,3,4分别表示自由之门及走了10分,20分,30分钟后重
回入口处的门号,那么
且
其中T1
为选择非自由之门返回入口处后到走出迷宫所需的时间。由题意
知,此时间的概率分布应该和T的分布是一样的,因此
利用全数学期望公式(4.1.13),得由此可解得,E(T)=65(分钟)。§4.2 方差、变异系数
(一)方差的定义
定义4.2.1 设随机变量X的数学期望存在,若E(X-E(X))2
存
在,则称E(X-E(X))2
为X(等价地,相应的分布)的方差,记
为D(X)Var(X)。其中D是英文deviation的第一个字母,Var是
variance的前三个字母(有时也可为V(X))。
从方差的定义可知,它反映了随机变量X的取值与其中心位置——
数学期望的平均偏离程度。这一特征当然也可以用变量对其平均值的绝
对偏离的平均值E|X-E(X)|来衡量,但由于在数学上绝对值的运
算不甚方便,因此改用具有同样效果而又便于运算的方差来代替。
方差的平方根 称为随机变量X的标准差或均方
差,记为SD(X),其中SD是英文standard deviation的縮写。它与方差
一样反映了随机变量与其中心位置的偏离程度。其优点是:它与随机变
量和数学期望具有相同的量纲。
按方差的定义可知,方差的计算可以看成随机变量的函数g(X)=
(X-E(X))2
的数学期望。值得注意的是函数表达式中的E(X)是
一实数。那么根据定理4.1.2可知:
(1)若离散型随机变量X的分布律为P(X=xi)=pi
,i=1,2,…,则X的方差为
(2)若连续型随机变量X的密度函数为f(x),则X的方差为
直接按定义计算方差往往比较麻烦,人们常常用下面的公式来计算
方差。定理4.2.1 若随机变量X的方差存在,则
证明 利用方差的定义及定理4.1.4,得
由上面的定理,显然可得
由于上式中的各项都是非负项,所以若E(X2)<+∞,可得D(X)<+
∞。其实反之也成立,即若D(X)<+∞,也可得出E(X2)<+∞。另
外,由于|X|?X2
+1,所以某一随机变量的方差若存在,则一定保证
了其数学期望的存在性。
例4.2.1 (泊松分布的方差)设随机变量X服从泊松分布π(λ)
(λ>0),则
又E(X)=λ,故D(X)=λ2
+λ-λ2
=λ。这表明泊松分布的数学期望与
方差都等于参数λ。
例4.2.2 (指数分布的方差)设随机变量X服从指数分布E(λ)
(λ>0),则
而即,指数分布的方差为其数学期望的平方。
例4.2.3 (标准正态分布的方差)设随机变量X服从标准正态分
布N(0,1),而
故D(X)=1-02
=1。
例4.2.4 对于例4.1.6中的M与N,分别求出其方差。
解 由M与N的密度函数,可得
(二)方差的性质
定理4.2.2 设随机变量X的方差存在,c为某一常数,则
(1)D(cX)=c2
D(X);
(2)D(X+c)=D(X);
(3)D(X)?E((X-c)2),其中当且仅当E(X)=c时等号成
立。
证明 按方差定义及上一节中提及的数学期望的线性性质,知(1)得证。同样利用方差定义,且上式当且仅当E(X)=c时等号成立,故得结论(3)。
一个常数c可以看成一个特殊的随机变量,其数学期望E(c)也
是c,因此这一特殊随机变量与其中心位置的偏差为0,即其方差为0;
反之,某随机变量X的方差为0,可见其取值非常集中,均集中在某一
点,此点即为其中心——数学期望。于是有下面的这一性质:
定理4.2.3 设随机变量X的方差存在,则D(X)=0当且仅当P(X
=c)=l,其中c=E(X)。
证明 若P(X=c)=1,其中c=E(X),那么根据方差的定义可
得D(X)=0,即定理的充分性得证。而定理的必要性证明需要用到切
比雪夫不等式,此不等式我们将在第五章中介绍,所以这一部分的证明
可以参见例5.1.2。
定理4.2.4 对任意的正整数n?2,设X1
,X2
,…,Xn
为两两独立的随
机变量,方差都存在。则X1
+X2
+…+Xn
的方差也存在,且
证明 注意到由于对任意的1?i
与Xj
两两独立,故由定理4.1.5知,故对任意i≠j,有
另外,结合定理4.2.2中的(1)可得:
推论4.2.1 对任意的正整数n?2,设X1
,X2
,…,Xn
为两两独立的随
机变量,方差都存在。则对任意的有限实数
的方差也存
在,且
例4.2.5 (二项分布的方差)设随机变量X服从二项分布B(n,p)(0
个相互独立且具有相同参数p的0-1分布随机变量的和,即令Yi
表示服从
参数同为p的0-1分布的相互独立的随机变量i=1,2,…,n,则
,于是
例4.2.6 (正态分布的方差)设随机变量X服从正态分布,据例4.2.3,知D(Z)=1,那么利用定理4.2.2,有
这表明正态分布中的参数σ2
表示的是此分布的方差,结合例4.1.14的
结果,我们知正态分布由其数学期望与方差完全确定。故常称为“期望
为μ,方差为σ2
(或标准差为σ)的正态分布”。而方差越小,正态分布的
取值就越集中在均值μ的附近。
(三)标准化变量与变异系数
定义4.2.2 若随机变量X的方差存在,那么称
为X的标准化随机变量。显然E(X)=0,D(X)=1,而且此类变
量是无量纲的。
事实上,引入标准化随机变量主要是为了消除由于计量单位的不同
而给随机变量带来的一些影响。例如:进行精密测量时,对于某物长度
的考察当然可以用厘米作为单位,得到随机变量X,也可以用毫米作为
单位,得到随机变量Y。那么Y=10X,从而X与Y的分布有所不同。这显
然不太合理。但通过标准化变换,就可以消除这种不合理性。之前常用
的标准正态变量也是一般正态变量经标准化变换得到的。
类似地,度量分布离散性的数字特征——方差也会由于这种量纲上
的不同而不同,如上例中,若X的方差为σ2
,那么Y的方差为100σ2
,若以
此认为Y较之X更为分散,显然是不合理的。为了消除量纲及取值大小
(包含单位不同)的影响,常用无量纲的来作为衡量指标,称之为变异系数(或称为标准离差率或单位风险,在
工程上,有时也称为变差系数),其中Cv是coefficient of variation的简
写。它反映了随机变量X在以它的中心位置为标准时,取值的离散程
度。那么,前一段落中提到的X与Y的变异系数显然是相同的,这也与实
际情况相符。
例4.2.7 已知甲乙两地居民的月收入分别服从N(1500,1502)
与N(2800,2202)(单位:元),试比较这两个地区贫富差异的程
度。
解 由题意知甲、乙两地居民月收入的方差分别为1502
,2202
,即
从方差的角度看甲地居民的贫富差异比乙地小。但也有人注意到了甲地
平均收入为1500,乙地的平均收入为2800相差较大,应该用变异系数来
反映两地区的贫富差异性较合适。两地的变异系数分别为
因此从变异系数角度看甲地居民的月收入的离散程度高于乙地,即甲地
居民的贫富差异比乙地大。
相比较方差(或标准差)而言,变异系数在比较两组量纲不同或均
值不同的变量时更能体现其优点。因此变异系数在概率论的许多分支中
都有应用,如:更新理论、排队理论、可靠性理论,等等。但是它也有
其缺陷,从它定义可知,如果一个随机变量的均值为0,那么此变量的
变异系数就没有意义。事实上,当变量的均值接近于0的时候,均值的
一点小小的变动也会对变异系数产生巨大影响,因此容易造成精确度上
的不足。§4.3 协方差与相关系数
对于多元随机变量,除了考虑每一个分量的中心位置和离散程度,借此来了解各个分量各自的部分特性外,还对于它们之间的关系感兴
趣。本节中我们将介绍反映两个变量间线性关系的两个数字特征——协
方差与相关系数。
(一)协方差
回想期望的性质之一——定理4.1.5,对于相互独立的随机变量X和
Y,当其期望都存在时,有E(XY)=E(X)E(Y),而此式等价于
那么当E{(X-E(X))(Y-E(Y))}≠0时,则X和Y一定不独
立,也就是存在某种相依关系,因此我们认为E{(X-E(X))(Y
-E(Y))}可以在一定程度上反映出X和Y的某种关系,对此给出下
面定义。
定义4.3.1 对于期望都存在的随机变量X和Y,当(X-E(X))
(Y-E(Y))的期望存在时,称
为X与Y的协方差,其中Cov是英文covariance的前三个字母。
按协方差的定义可知,协方差的计算可以看成二元随机变量的函数
的数学期望,那么根据定理4.1.3可知:
(1)若二元离散型随机变量(X,Y)的联合分布律为P(X=xi
,Y
=yj)=pij
,i=l,2,…,j=1,2,…,则X与Y的协方差为(2)若二元连续型随机变量(X,Y)的联合密度函数为f(x,y),则X与Y的协方差为
直接按定义计算协方差往往比较麻烦,在实际应用中常常用下面给
......
主 编 张帼奋
副主编 黄柏琴 张彩伢《概率论、数理统计与随机过程》
编委会
主 编 张帼奋
副主编 黄柏琴 张彩伢
编 委 张 奕 赵敏智 黄 炜图书在版编目(CIP)数据
概率论、数理统计与随机过程张帼奋主编.—杭州:浙江大学出版
社,2011.7
ISBN 978-7-308-08852-7
Ⅰ.①概… Ⅱ.①张… Ⅲ.①概率论-高等学校-教材②数理统计
-高等学校-教材③随机过程-高等学校-教材 Ⅳ.①021
中国版本图书馆CIP数据核字(2011)第134518号
概率论、数理统计与随机过程
主 编 张帼奋
副主编 黄柏琴 张彩伢
责任编辑 余健波
封面设计 续设计
出版发行 浙江大学出版社
(杭州天目山路148号 邮政编码310007)
(网址:http:www.zjupress.com)
排 版 杭州中大图文设计有限公司
印 刷 德清县第二印刷厂
开 本 787mm×1092mm 116
印 张 18.25
字 数 558千版 印 次 2011年7月第1版 2011年7月第1次印刷
书 号 ISBN 978-7-308-08852-7
定 价 32.00元
版权所有 翻印必究 印装差错 负责调换
浙江大学出版社发行部邮购电话 (0571)88925591前言
本书是为非统计专业本科生编写的教科书,也可以作为有微积分基
础的科研工作者学习与使用概率论,数理统计与随机过程的基本概念与
方法的参考材料。
本书分为三部分:第一部分(第一章至第五章)是概率论部分,主
要介绍概率论的基本知识,包括一元,二元离散型随机变量和连续型随
机变量的分布,数字特征等;第二部分(第六章至第九章)是数理统计
部分,介绍了统计量与抽样分布,参数估计,假设检验,方差分析与回
归分析;第三部分(第十章至第十三章)介绍随机过程的基本知识,马
尔可夫链,泊松过程,布朗运动和平稳过程。各部分的教学时数都约为
24学时,概率论部分的教学时数可以稍多些。数理统计与随机过程的内
容是独立的,可以根据需要开设概率论与数理统计或概率论与随机过程
课程。
本书的主要特点有:(1)在每章的习题前列出了思考题,使读者
对每章的内容有更清晰的梳理;(2)在某些章节尤其是数理统计部分
的例子后介绍了Excel软件应用,使读者不仅掌握概率统计的原理,还
能对大量复杂的数据运用软件进行直接分析;(3)例题和习题的选取
上尽可能贴近生活,兼顾趣味性,有实际意义。
本书的第一章到第三章由黄柏琴编写;第四,第五章由黄炜编写;
第六,第九章由张奕编写;第七,第八章由张彩伢编写;第十,第十一
章由赵敏智编写;第十二,第十三章由张帼奋编写,最后的统稿由张帼
奋完成。编者中除了张彩伢是浙江大学城市学院教师,其余都是浙江大
学教师。书中的部分介绍,例题和习题参考了书后所列的书目,在此特
向有关的作者和出版社表示衷心的感谢。
参加本书编写的教师都长期从事教学科研工作,有丰富的教学实践
经验,书中的不少内容是我们教学科研工作的总结,愿与广大读者交流
分享。
张立新教授对本书的讲义进行了审阅,并提出了宝贵的意见,在此
也向他表示由衷的谢意。另外还要感谢其他对本教材的讲义提出意见和
给予帮助的老师和研究生等。在写作过程中我们努力做到内容由浅入深,所选例题典型新颖,解
题过程条理清晰.由于编者水平有限,书中可能还有不少的缺陷,恳请
各位同行,专家和广大的读者朋友批评指正。
本书编委会
2011年5月目录
前言
第一章 概率论的基本概念
§1.1 样本空间、随机事件
§1.2 频率与概率
§1.3 等可能概型
§1.4 条件概率
§1.5 事件的独立性与独立试验
思考题一
习题一
第二章 随机变量及其概率分布
§2.1 随机变量
§2.2 离散型随机变量
§2.3 随机变量的概率分布函数
§2.4 连续型随机变量
§2.5 随机变量函数的分布
思考题二
习题二
第三章 多元随机变量及其分布
§3.1 二元离散型随机变量
§3.2 二元随机变量的分布函数
§3.3 二元连续型随机变量
§3.4 随机变量的独立性
§3.5 二元随机变量函数的分布
思考题三
习题三
第四章 随机变量的数字特征
§4.1 数学期望
§4.2 方差、变异系数
§4.3 协方差与相关系数
§4.4 其他数字特征
§4.5 多元随机变量的数字特征
思考题四
习题四
第五章 大数定律及中心极限定理§5.1 大数定律
§5.2 中心极限定理
思考题五
习题五
第六章 统计量与抽样分布
§6.1 随机样本与统计量
§6.2 x2分布,t分布,F分布
§6.3 正态总体下的抽样分布
§6.4 附录
思考题六
习题六
第七章 参数估计
§7.1 点估计
§7.2 估计量的评价准则
§7.3 区间估计
§7.4 正态总体参数的区间估计
§7.5 非正态总体参数的区间估计
思考题七
习题七
第八章 假设检验
§8.1 假设检验的基本思想
§8.2 单个正态总体参数的假设检验
§8.3 两个正态总体参数的假设检验
§8.4 假设检验与区间估计
§8.5 拟合优度检验
思考题八
习题八
第九章 方差分析与回归分析
§9.1 单因素方差分析
§9.2 多因素方差分析
§9.3 相关系数
§9.4 一元线性回归
§9.5 多元回归分析
§9.6 回归诊断
§9.7 附录
思考题九
习题九第十章 随机过程基本概念
§10.1 定义和例子
§10.2 有限维分布
§10.3 均值函数和协方差函数
思考题十
习题十
第十一章 马尔可夫链
§11.1 马尔可夫链的定义
§11.2 有限维分布
§11.3 常返和暂留
§11.4 平稳分布
思考题十一
习题十一
第十二章 泊松过程与布朗运动
§12.1 独立增量过程
§12.2 泊松过程
§12.3 布朗运动
思考题十二
习题十二
第十三章 平稳过程
§13.1 平稳过程的定义
§13.2 各态历经性
§13.3 平稳过程的功率谱密度
§13.4 线性系统中的平稳过程
思考题十三
习题十三
附表
附表1 几种常用的概率分布表
附表2 标准正态分布表
附表3 t分布表
附表4 x2分布表
附表5 F分布表
附表6 柯尔莫哥洛夫检验临界值Dn,α
附表7 柯尔莫洛未检鸟金统计量Dn的极限分布
附表8 W检验统计量W的系统αi(n)的值
附表9 W检验统计量W的α分位数Wα
附表10 D检验统计量Y的α分位数Yα思考题、习题参考答案
参考文献第一章 概率论的基本概念
自然界的现象可以分为两大类:一类为必然现象,另一类为随机现
象。
所谓必然现象,是指在一定的条件下必然发生的现象。例如:在一
个标准大气压下,水加热到100℃一定会沸腾;向上抛一重物,一定会
落到地面上;月亮一定沿某一轨道绕地球运转,等等。研究这些必然现
象中的数量关系,常常采用微积分、代数、几何及其他一些数学方法。
所谓随机现象,也称为偶然现象,是指在一定条件下具有多种可能
发生的结果,而对于究竟发生哪一个结果事先不能肯定的现象。例
如:“明天天气”可能是晴,也可能是阴或雨;从一批产品中任意抽取一
件产品,该产品可能是合格品,也可能是不合格品;同一工人在同一台
车床上用同样的材料加工同类型的轴,其直径也不会完全相同;某一时
刻某柜台的顾客数可能为0,1,2,3,…,等等,这些仅仅是“瞬息万
变”的大千世界中的一点点事实。从表面上看,随机现象完全由偶然性
在起支配作用,没有什么必然性。其实,这些现象有一个共同的特点:
在一定的条件下,当我们重复观察随机现象的时候,就会发现随机现象
的出现有其规律性。例如:从一大批产品中,每抽一件产品,该产品是
合格或是不合格是随机的,这是现象具有偶然性的一面;然而,当重复
抽取产品时,不合格品率是稳定的,这就是现象具有的必然性的一面。
再如,当一辆汽车按正常操作通过某一地段时,事先无法确切知道会不
会发生交通事故,即带有偶然性;但经过大量的观察,发现某一地段发
生交通事故比较多,因此就在这一地段的路边立了一块“事故多发地
段”的牌子(这就是必然的一面,即有规律性的一面),提醒人们引起
注意。由此可见,随机现象的出现是偶然的,但在大量重复试验(观
察)中,随机现象隐藏着必然的规律性,这种固有的规律性称为统计规
律性。概率论、数理统计与随机过程就是研究随机现象数量规律性的学
科。§1.1 样本空间、随机事件
(一)样本空间、随机事件
为了精细地考察一个随机现象,必须分析这个随机现象的各种结
果,只有弄清了一个随机现象的各种结果,才能进一步研究这个随机现
象的各种结果出现的可能性。对随机现象作一次观察(或记录、或试
验)称为随机试验(random experiment),这些试验具有以下特点:
(1)可以在相同的条件下重复进行;
(2)每次试验可能出现的结果不止一个,但能事先明确试验的所
有可能结果;
(3)试验完成前不能确定哪个结果会出现。
本书中以后提到的试验都是指随机试验。
称随机试验的所有可能结果构成的集合为样本空间(sample
space),记为S.样本空间S中的每一个元素,即试验的每一个结果称
为样本点(sample point)。
观察随机现象时,人们常常关心某些特定的结果,这些结果可能出
现,也可能不出现。在随机试验中,称那些可能发生又可能不发生的结
果为随机事件(random event),简称事件。特别地,称试验的每一个
结果(即样本点)为基本事件。
我们常用集合的方法描述样本空间及随机事件,那么随机事件即为
样本空间的一个子集。
例1.1.1 投掷一枚硬币,试验的结果有2个:“正面朝上”,“反面朝
上”,故该试验所对应的样本空间由上述2个基本事件构成,简记为
例1.1.2 一射手向一目标射击3次,观察他的击中次数,可能为“击
中0次”,“击中1次”,“击中2次”,“击中3次”,即该试验有这4种可能结果,每一个结果都是一个基本事件,所以该试验所对应的样本空间可以
简记为
记A={至少有1次击中}={1,2,3} S;B={击中次数
不到2次}={0,1} S.A,B均为随机事件。
例1.1.3 记录一批标注重量为50(kg)的袋装大米的重量x与农药
残留量y,对应的样本空间为
其中y0
为农药最高残留量。
例1.1.4 从15个同类产品(其中12个正品,3个次品)中任取4个产
品,观察取得的次品数,则对应的样本空间为
{至少有2个正品}及{恰有2个正品}均为随机事件。
当某一事件所包含的一个样本点发生时,我们就称该事件发生。例
如,在例1.1.2中,A={1,2,3},若射手“恰好击中1次”时,即A所包
含的一个样本点出现,那么我们就称事件A发生;当射手“恰好击中2
次”时,我们亦称事件A发生;当射手“恰好击中3次”时,我们同样称事
件A发生。
特别地,若将样本空间S亦视为一事件,因为S包含了试验所有的可
能结果,因此在任何一次试验中,事件S一定会发生。我们称这种每次
试验必然发生的事件为必然事件,用S来表示。与之相对应地,称在任
何试验中都不可能发生的事件为不可能事件,记为?。考察例1.1.4中的2个事件:{4个都是次品}和{至少有1个正
品},前者是不可能事件,后者是必然事件。
(二)事件的相互关系及运算
在研究随机现象时,为了掌握复杂事件的统计规律,我们常常需要
研究事件之间的相互关系及运算。
前面我们已经用集合描述了样本空间与随机事件,下面我们再用集
合论的方法来定义与理解事件的相互关系及运算。
1.事件的包含与相等
设A,B为同一样本空间S中的两个事件。若当事件B发生时一定导
致A发生,则称事件A包含事件B,记为
,记
为A=B,即称事件A与B相等。
2.事件的运算
同样假设以下参与运算的事件都在同一样本空间中。
事件A∪B在集合论中理解为由集合A与B的元素合并到一起构成的
新的集合,现在A,B为随机事件,A∪B为一个新的事件。事件A∪B包
含了A和B的所有样本点,这些样本点发生时,A∪B发生。故当事件
A,B至少有一发生时,A∪B发生。因此有下面的定义:
为事件A与事件B的和事件。同样,称
为n个事件 的和
事件;称为可列个事件 的和事件。
而在集合论中,A∩B表示由A,B两个集合的公共元素组成的新的集
合,即A∩B发生当且仅当事件A,B同时发生。故称
为事件A与事件B的积事件,也可表示成A?B,或表示成AB。类似可以定
义:
为n个事件 的积
事件;称
为可列个事件 的积事件。
对于“A不发生”事件,称之为A的逆事件,记作 ,即
注意到 ,同时 。故A与 互逆,又称A与 为对立事件。
A与B的差事件,记为A—B,即
因此, 。
我们可以借助以下的图形(见图1.1.1),表示以上事件的关系和运
算:
图1.1.1
和、交与逆事件具有以下的运算规则:
交换律:;
结合律:;
分配律:;
德摩根定律(De Morgan's laws):即“n个事件至少有一发生”的逆事件为“这n个事件都不发生”;“n个事件
都发生”的逆事件为“这n个事件至少有一个不发生”。
定义1.1.1 设A,B为两随机事件,当AB=?时,称事件A与事件B
不相容(或互斥)。
也即当A与B不能同时发生时,称A,B不相容。我们注意到“样本空
间中的样本点两两不相容”。
例1.1.5 抛一颗骰子,设
,6.再设A={得到偶数点},B={得到奇数点},C={得到1点或
3点}。则
显然 ;又AC=?,故A与C不相容,又
,故A,B互逆。
概率论中常有以下定义:由n个元件组成系统,若有一个损坏,则
系统就损坏,此时称该系统为串联系统;若有一个不损坏,则系统不损
坏,此时称该系统为并联系统。例如,一个凳子是由4条腿、凳板、靠
背共6个部分组成,如果其中一个部分损坏,我们就认为这把凳子坏
了,那么这把凳子就是一个由6个部件组成的串联系统。
例1.1.6 由“个部件组成的系统,设。则有§1.2 频率与概率
(一)频率
前面已经提到,我们的目的是要研究随机现象的数量规律性,为此
我们首先提出频率的概念。
在一定的条件下,设事件A在n次重复试验中发生nA
次(称nA
为A在
这n次试验中发生的频数),称比值 为事件A在
这n次试验中发生的频率(frequency),记为 ,例1.2.1 从市场上抽查了某品牌的一种液态奶制品30件,其中有20
件被检出了某种物质含量超标,则事件“检出某物质含量超标”在这30
次试验中发生的频率为 。
事件A发生的频率越大,人们就会感到A发生的可能性越大,频率
越小,就有这一事件不易发生的感觉,所以频率是人们对事件发生的可
能性大或小的第一认识。
事件的频率具有以下性质:
(1)对任一事件 ;(2) ;
(3)当事件A与B不相容时,。
性质(3)可以推广,当
两两不相容时,例1.2.2 某厂每天从当天的产品中抽取50件,检查其是否合格,记
录于表1.2.1:
表1.2.1
表1.2.2
实验者 n n A fn
(A )
德摩根 2048 1061 0.5181
蒲丰 4040 2048 0.5069
K.皮尔逊 12000 6019 0.5016
K.皮尔逊 24000 12012 0.5005
例1.2.3 抛硬币试验,在相同的条件下将一枚硬币抛n次(你不妨
一试),设A={出现正面},当“较小时, 的变化范围
较大,但人们发现,当n渐渐增大时, 的值渐渐地稳定在0.5附近。以下是几个世界著名的大统计学家抛硬币的试验结果(列
于表1.2.2):
无数事实告诉我们,在大量试验中(即当n充分大时),任一随机
事件A的频率 具有稳定性, 会稳定于一个
常数p(0≤p≤1)附近,这个数是由事件A的属性所决定的。这给了我们
一个机会,一个用数量来描述事件A发生的可能性大小的机会。
(二)概率
有一种定义概率的方法(称之为概率的统计性定义)是:设某一随
机试验所对应的样本空间为S,对S中的任一事件A,A的频率
的稳定值p定义为A的概率,记为P(A)=p。
虽然上面的定义很直观,很易理解,且人们也常用这样的思路来解
释概率,但也存在问题。事实上,人们常常不易知道 的
稳定值p,因而我们采用以下公理化的定义。
定义1.2.1 设某一随机试验所对应的样本空间为S.对S中的任一事
件A,定义一个实数P(A),满足以下三条公理:
(1)P(A)≥0;
(2)P(S)=1;
(3)对S中的可列个两两不相容的事件
,有则称为P(A)为A的概率(probability),P(?)为概率测度。
值得注意的是,对于有限个两两不相容的事件的和事件有
以上定义的概率有以下性质:
(1) ;
因为 ,两边求概率(注意到),即得。
特别地, ,可得。
(注意:若有P(A)=0,不一定能得出A=?。)
(2)当 时,必有P(A)≥P(B);
因为当 时,。而 ,故P(A)≥P(B)。进而可得P(A)≤P(S)=1。
(3)概率的加法公式:性质3可以推广:
例1.2.4 设甲、乙两人向同一目标进行射击,已知甲击中目标的概
率为0.7,乙击中目标的概率为0.6,两人同时击中目标的概率为0.4,求
目标不被击中的概率。
解
而
,所以
例1.2.5 设甲、乙、丙三个人去参加某个集会的概率均为0.4,且
甲、乙、丙中至少有两个人去参加的概率为0.3,三人同时参加的概率
为0.05。求甲、乙、丙三人至少有一人参加的概率。
从以上两个例题可以看出,解这类题,第1步:要设随机事件;第2
步:要明确写出已知什么及要求什么;第3步:写出事件的运算式与概率运算式,求出概率。§1.3 等可能概型
在某些随机试验中,我们常假设样本空间中样本点出现的可能性相
等。例如,抛硬币试验,S={正面,反面},我们常假设出现正面与
反面的概率相等。
定义1.3.1 一个随机试验,如果满足下面两个条件;
(1)样本空间中样本点数有限(有限性);
(2)出现每一个样本点的概率相等(等可能性)。
则称这个试验问题为古典概型,又称等可能概型。
若设一等可能概型的样本空间为
,则由定义1.3.1知。任一随机事件。由样本点两两不相容的性质,知
这就是说,在等可能概型中,任一事件A的概率为
因此,在古典概型中,求随机事件概率的问题就可以转化为数样本
点数的问题,这常要用到组合数学。
例1.3.1 从一付牌(去掉两个王,共52张)中随机取两张,求“恰是一红一黑”的概率。
解 设A={恰是一红一黑}。
(1)>若是不放回抽样(即第一次抽出1张,不放回,再抽第二
张),则
(2)>若是放回抽样(即第一次抽出1张后,放回,再抽第二
张),此时的样本空间为
则
例1.3.2 (抽签问题)袋中有编号为1,2,…,n(n>1)的n个
球,其中有a个红球,b个白球(a+b=n)。从中每次摸一球,不放
回,共摸n次。设每次摸到各球概率相等。求第k(l≤k≤n)次摸到红球
的概率。
解 设Ak
={第k次摸到红球},k=1,2,…,n。
解法1 假设我们视n次摸出的球号的先后排列为一个样本点,则样
本空间中共有n!个样本点。由题意知,出现每一个样本点的概率相
等,而第k次为红球共有a(n-1)!个样本点。所以
解法2 若我们n个同学去摸球,我们只关心哪几个同学摸到红球为试验的结果,即假设视“哪几次摸到红球”为样本点,则样本空间总样本
点数为由题意知,出现每一个样本点的概率相等。如果Ak
发生,即第k
次一定为红球,只要在余下的(n—1)次中决定(a—1)次就行。故
解法3 若视第k次摸到的球号为样本点,则样本空间中共有n个样
本点,其中有a个样本点使得Ak
发生,故
以上三种方法计算得到:在抽签问题中,第k(l≤k≤n)次摸到红球
的概率与k无关。
例1.3.3 (配对问题)一个小班共有n个学生,分别编上1,2,…,n号,在中秋节前每人做一件礼物相应地编上1,2,…, n号。将
所有礼物集中放在一起,然后让每个同学随机地取一件(即,每次取到
每一件礼物是等可能的),求没有人取到自己礼物的概率。
解 先求“至少有一个人拿到自己的礼物”的概率。设
由概率的加法公式,得
如果将先后取到的礼物的编号(即排列)作为一个样本点,例如,(1,2,???,n)表示n人都取到了自己的礼物,那么共有n!个样本
点,由题意知出现每一个样本点的概率相等。当Ai
发生时,即i号配对其
余(n—1)个号可以任意的排列,故当n充分大时,上式的值近似于 。§1.4 条件概率
(一)条件概率
我们先来看一个例子,设一批产品的合格品率为80%,合格品中
90%是优质品,从中任取一件,设A={取到合格品},B={取到优
质品},则取到优质品的概率显然为72%。若把考虑问题的范围缩小,即,只考虑已知取到的一件是合格品,那么取到的这一件合格品是优质
品的概率应为90%,也就是说,如果把取到所有的合格品的概率记为
1,那么取到的一件是优质品的概率为90%,常记为P(B|A)=90%。
P(B)=72%与P(B|A)=90%是在两个不同的样本空间中对事
件B的概率进行度量,后者是将A作为新的样本空间。
定义1.4.1 如果P(A)>0,那A发生的条件下B的条件概率
(conditional probability)为
例1.4.1 将一枚均匀的硬币抛两次,已知“至少有1次正面”的条件
下,求“两次都是正面”的概率。
解 设Hi
={第i次为正面},i=1,2,B={至少有一次为正
面},C={两次均为正面}。
样本空间为。因为硬币是均勾的,故这是一个等可能概型。
解法1 显然
,故解法2 将B视为缩减了的样本空间S1
,则
这也是一等可能概型。在S1
的3个样本点中只有一个样本点使C发生,故
解法1是用条件概率定义求解,解法2是利用我们对条件概率的理
解,用缩减了的样本空间来求解,两种方法都行。
例1.4.2 一袋中有5个红球,4个白球,从中每次摸一球,不放回抽
样,抽4次。(1)已知前两次中至少有一次摸到红球,求前两次中恰有
一次摸到红球的概率;(2)已知第4次摸到的是红球,求第1次和第2次
摸到的都是红球的概率。
解 设Ai
={第i次摸到红球},i=1,2,3,4。再设B={前两次
中至少有一次摸到红球},C={前两次恰有一次摸到红球}。
(1)>题中要求的是P(C|B)。
(2)即求。由§1.3的例1.3.2,可知 。而
所以
其实,任何事件的概率都是在一定条件下给予的值,也即概率本身
就是有条件的。上面定义的条件概率无非是在新的样本空间下的概率度
量,因此条件概率同样具有一般的概率性质。
例如:当P(C)≠0时,有
(1) ;
(2)当 时,;
(3)。
推广之,(二)乘法公式
由条件概率的定义知,当P(A)≠0,P(B)≠0时,即两个事件积事件的概率等于一个事件的概率乘以在这个事件发生的条
件下另一个事件的条件概率,称此等式为概率的乘法公式。
推广之,当
时,有
为了证明(1.4.3)式,对等式的右边利用条件概率的定义,可得
对应于条件概率(假设以下的条件概率均有意义),则相应地有
例1.4.3 设一社区“3口之家”占了70%,且有40%的家庭“至少有1
人职业为教师”,在“3口之家”中有30%的家庭“至少有1人职业为教
师”。在这社区中随机找一户,(1)求这一户既不是“3口之家”又没有
教师的概率;(2)已知这一户没有教师,求这一户是“3口之家”的概
率。
解 设A={这一户是“3口之家”},B={这一户有教师},由题
意知,(1)P(A)=70%,P(B)=40%,P(B|A)=30%,得。
所要求的概率为
例1.4.4 某人参加某种技能考试,已知第1次考合格的概率为
50%,若第1次没有合格,通过努力,第2次能考合格的概率为60%;若
第1,2次均不合格,则第3次能考合格的概率为70%,求此人最多3次能
考合格的概率。
解 设Ai
={第i次考合格}i=1,2,3,B={最多3次能考合
格}。
解法1 注意到。所以
解法2 由于 ,故
(三)全概率公式、贝叶斯公式假设A,B为随机事件,那么总是有 ,又因为AB与 互不相容,可得
(1.4.6)式很重要,说明当直接计算A的概率比较困难时,可以先将A
分解成不相容的两部分Ab与 ,当然B常常与A有密切的关系。
它使得我们能够通过第二个事件b发生与否来求得A的概率。注意到
,故(1.4.6)式实际上是条件概率的加权平
均。式中重要的是如何寻找合适的B。
为了将(1.4.6)式推广至更一般的情形,下面先给出一个定义。
定义1.4.2 设S为某一随机试验的样本空间,为该试验的一组事件,且满足
则称 为S的一个划分,或称为S的一
个完备事件组。
上述定义中的两条,通俗而言,即 两同时发
生是不可能的,而至少有一发生又是必然的。其实,当样本空间S的样
本点有限时,这些样本点就是S的一个划分。
若A是S的一个事件, 是S的一
个划分,则参照导出(1.4.6)式的方法,我们也可以将A分解成两两不相容的事件的和,即
两边求概率,得 。于是
我们就可以得到下面的定理:
定理1.4.1 设S为某一试验的样本空间,A为该试验的事件。设
是S的一个划分,且。则
称(1.4.7)式为概率的全概率(total probability)公式。
同样(1.4.7)式的关键是找到一组合适的划分。
在上述定理的条件下,有
,故
当 ,n时,有
称(1.4.8)式为条件概率的全概率公式。
定理1.4.2 设S为某一试验的样本空间,A为该试验的事件,且P(A)≠0。设 是S的一个划分,且 。则对任意k
=1,2,…,n,称(1.4.9)式为概率的贝叶斯(Bayes)公式。
在利用贝叶斯公式时,其中的P(Bj)(j=l,2,…,n)的概率是
事先假设(或者根据以往的资料或是根据经验的累积)知道的,常称
P(Bj)为先验概率,而当事件A发生时,我们可以对Bj
发生的概率进行
重新认定(或修正),常称 为后验概率。
例1.4.5 某公司有甲、乙两人,已知甲近期出差的概率为0.7,又
已知如果甲出差则乙出差的概率为0.1,如果甲不出差则乙出差的概率
为0.6。(1)求乙近期出差的概率;(2)已知乙已经出差在外,求甲
近期出差的概率。
解。
(1)乙近期出差的概率为
(2)已知乙已经出差在外,求甲近期出差的概率为例1.4.6 设有3个箱子,第1箱装有3个白球和5个红球,第2箱装有2
个白球和2个红球,第3箱装有5个白球和2个红球。现随机地取一箱,再
在这一箱中随机取2次,每次取一球,不放回抽样。(1)求第一次取到
的是白球的概率;(2)已知第二次取到的是白球,问取到的是第1,2,3箱的概率分别为多少?
解 设Ai
={取到第i箱},i=1,2,3。Bj
={第j次取到白球},j
=1,2。那么A1
,A2
,A3
构成了样本空间的一个划分。
先来求 ,即在取到第1箱的条件下,第2
次摸到白球的概率。由§1.3例1.3.2知,,同理可得。从而 。故
同理其实,求P(B2)也可以用以下方法:
其中的。
另外,读者应该注意到 ,这一点事先就应知道。
例1.4.7 某地发生了一起当地人驾车偷盗事件,调查员有80%的把
握认为是男子A所为,现更有证据表明当事车为B型车,B型车在当地占
了30%。在已知男子A当天开的也是B型车的条件下,调查员认为男子A
偷盗的把握有多少?
解 设A={男子A为偷盗者},B={男子A当天开的是B型
车}。则
例1.4.8 有3个箱子,第1箱中装有5件为正品,2件为次品,第2箱
中有4件正品,2件次品,第3箱中有3件正品,2件次品。现从第1箱中随
机取1件放人第2箱,再从第2箱中随机取1件放人第3箱,再从第3箱中取
1件,求最后取出的是次品的概率。解 设A,B,C分别为从第1,2,3箱中取到次品事,易得。则
由条件概率的全概率公式知
同理可得
因此。§1.5 事件的独立性与独立试验
从§1.4中的一些例题可知,若A,B均为随机事件,一般情形下,不等于P(A)。也就是说事件B发生的条件会改变事件A发生
的概率。但也有不改变的,例如,某种彩票每次公布的最后两个数都是
从0到9这10个数字中随机取1个数,如果记Ai
={倒数第i位数小于
5},i=1,2,则有
,也就是说A1
发生并不影响A2
发生的可能性。由概率的乘法公式知,此
时
,易见此式中A1
,A2
是对称的。这时我们称A1
,A2
是相互独立的。
定义1.5.1 设A,B为两随机事件,当
成立时,称事件A,B相互独立(independence)。
定理1.5.1 当P(A)?P(B)≠0时,“事件A与事件B相互独立”等价
于“条件概率等于无条件概率”,即
定理1.5.2 当事件A与事件B相互独立时,均相互独立。
证明 因为 ,两边求概率并移项得当事件A与事件B相互独立时,故A与 互相互独立。由此可进一步得 均相
互独立。
定义1.5.2 设A,B,C为三个随机事件,当
都成立时,称事件A,B,C两两独立。
如果同时还满足P(ABC)=P(A)?P(B)?P(C),则称事件
A,B,C相互独立。
应注意到相互独立一定是两两独立的,而两两独立时不一定是相互
独立的。
例如,设一随机试验的样本空间为
,且是等可能概型,记。那么有。同理有
两两独立。不互相独立。
定义1.5.3 设n个事件
,若对任意的
,都有
成立,则称事件
相互独立。
如果对于可列个事件,若其中任意的有限个事件相互独立,则称这
可列个事件相互独立。
最后,我们来定义试验的独立性,假设所考虑的概率试验是由一系
列子试验组成。例如,某一种彩票一期一期地不断开奖,就可以把每一
次开奖看作一个子试验,而且这一期开奖的结果不影响其他期的开奖结
果。像这样的试验结果互不影响的一系列试验称为独立试验。如果各个
子试验是在相同条件下进行的,那我们就称这些试验为重复试验。
在实际问题中,我们常常不是用独立的定义去验证事件的独立性,而是根据实际情况来判断。例如,我们可以认为某一批袋装味精的重量
(克)与纯味精的含量(%)是独立的;又如,甲、乙两人同时向各自
的靶位射击,注意这儿的“同时”两字,这就意味着两个人的射击结果是
互不影响的,所以事件“甲命中”与“乙命中”是相互独立的。
图1.5.1
例1.5.1 有5个独立元件组成的系统(如图1.5.1所示),设每个元件运行正常的概率为户p,0
率。
解 设Ai
={第i个元件运行正常},i=1,2,3,4,5。由题意
知, 相互独立。并设A={系统
运行正常},则 ,那么
图1.5.2
用缩减了的样本空间理论求解 的值为p1
,p2
即为图1.5.2所示系统运行正常的概率,故
又若记 的值为p2
,p2
即为图1.5.3所示系统运行正常的
概率,同理可得图1.5.3
所以
例1.5.2 一袋中有编号为1,2,3,4共四个球,每回从袋中有放回
地取两次(一次一个球,假设取到每一个号码的概率相等),并记录号
码之和。这样独立重复地试验,求“和等于3”出现在“和等于5”之前的概
率。
解 设A={“和等于3”出现在“和等于5”之前},B={第一次号码
之和为3},C={第一次号码之和为5},D={第一次号码之和既不
是3,也不是5}。
显然每次“号码和为3”的概率为 ,“号码和为5”的概率为
,“号码和既不是3又不是5”的概率为 ,故
由全概率公式,得在已知第一次号码和既不是3,也不是5的条件下,求A的条件概率问
题,相当于重新开始考虑A的概率,因为试验是独立的,即第一次结果
不影响A发生的概率,所以P(A|D)=P(A),故
例1.5.3 某技术工人长期进行某项技术操作,他经验丰富,因嫌按
规定操作太过烦琐,就按照自己的方法进行,伹这样做有可能发生事
故。设他每次操作发生事故的概率为p,0
次操作。求:(1)n次都不发生事故的概率;(2)至少有一次发生事
故的概率。
解 设A={n次都不发生事故},B={n次中至少一次发生事
故},Ci={第i次不发生事故},i=1,2,…,n。由题意知,相互独立,且。故
注意到, ,也就是说,虽然每次发生事
故的概率p很小,但只要次数多(n充分大),至少有一次发生事故的概
率就会大,甚至接近于1总之,随着独立重复试验次数的增多,“小概率
事件”“至少有一次发生”的概率在渐渐增大。思考题一
1.设A,B为两随机事件,当P(AB)=0时,A与B不相容,对
吗?
2.随机事件A的频率 是个变化着的数,而概率P(A)
是一个定数,对吗?当n充分大时, ,对吗?
3.试举例说明P(AB)与P(B|A)的不同意义。
4.因为随机事件A发生时A∪B一定发生,故P(A|A∪B)=1,对
吗?
5.当 时,随机
事件A,B独立与不相容可能同时成立吗?A,B独立能用Venn图(见图
1.1.1)表示吗?
6.设随机事件A,B,C满足P(ABC)=P(A)?P(B)
·P(C),问A,B,C一定相互独立吗?习题一
1.为了解吸烟(草)对人体健康是否有影响,对一社区居民进行
抽样调查,分别用0,1,2表示不吸烟,少量吸烟及吸烟较多,再
用a,b,c表示身体健康,一般及有病。例如:(0,a)就表示抽到的
居民是不吸烟的健康者。
(1)问试验的样本空间共有多少个样本点?
(2)设A={抽到的居民身体健康},试写出A所包含的样本点;
(3)设B={抽到的居民不吸烟},试写出B所包含的样本点。
2.设A,B,C为3个随机事件,请用事件的运算关系式表示:
(1)A,B,C至少有2个发生;
(2)A,B,C最多有1个发生;
(3)A,B,C恰有1个不发生;
(4)A,B,C至少有1个不发生。
3.设A,B为2个随机事件,判断以下说法的对错,并说明理由。
(1)
,则一定有A,B不相容;
(2)P(A)=1,则一定有A=S;
(3)P(B)=0,则一定有B=?;
(4)P(A)=0.6,P(B)=0.7,则A,B一定相容。
4.设事件A与B不相容,P(A)=0.3,P(B)=0.6。求:(1)A与B至少有一发生的概率;
(2)A与B都不发生的概率;
(3)A不发生同时B发生的概率。
5.设A,B,C为3个随机事件,已知P(A)=P(B)=P(C)=
0.4,且A,B,C至少有2个发生的概率为
0.3,A,B,C同时发生的概率为0.05,求A,B,C都不发生的概
率。
6.一袋中有10个球,其中8个是红球。每次摸一球,共摸2次,在
放回与不放回抽样两种方式下,分别求:
(1)“两次均为红球”的概率;
(2)“恰有1个红球”的概率;
(3)“第2次是红球”的概率。
7.一30人的班级中有两个“王姓”的学生,将全班学生随机排成一
排,求:
(1)两个“王姓”学生紧挨在一起的概率;
(2)两个“王姓”的学生正好一头一尾的概率。
8.一盒子中有2个红球,3个黑球,2个白球(共7个球)。每次摸
一球(不放回),共摸3次。求:
(1)摸到球恰是1红1黑1白的概率;
(2)摸到的全是黑球的概率;
(3)第1次为红且第2次为黑球第3次为白球的概率。
9.编号为1,2,…,9的9辆车,随机地停入编号为1,2,…,9的
9个车位中,若车号与车位号一样称该车配对。求:(1)1号车配对的概率;
(2)1号车配对而9号车不配对的概率;
(3)1号车,9号车都配对,但其他均不配对的概率。
10.设A,B为两随机事件,且已知
,求:
(1) ;
(2) ;
(3) 。
11.设一社区订A,B,C报的家庭分别占50%,30%,40%。且已
知一家庭订了A报的条件下再订B报的概率为20%,订了C报的条件下又
订A报或B报的概率为60%。随机找一家庭,求该家庭至少订A,B,C报
中的一种的概率。
12.某企业中有45%为女职工,10%的职工在管理(技术,质量,行政)岗位。5%的职工为管理岗位的女职工。在该企业中随机找一位
职工。
(1)>已知该职工为女职工的条件下,求该职工在管理岗位的概
率;
(2)>已知该职工在管理岗位,求该职工为男职工的概率。
13.从1,2,3,4,5中取一数X,再从1,2,…,X中取一数Y,求{Y=2}的概率。
14.一架子上有4把枪,其中3把是调试好的,1把未调试。设某君用调试好的枪射击命中率为60%,用未调试的枪命中率为5%。此人从4
把枪中随机地取一把进行射击。
(1)求命中的概率;
(2)已知此人命中了,求取到的是未调试的枪的概率。
15.对某证券营业点进行统计。得知入市时间在1年以内的股民
赢、平、亏的概率分别为10%,20%,70%;人市时间在1年以上但不
到4年的股民赢、平、亏的概率分别为20%,30%,50%,入市时间于4
年的股民赢、平、亏的概率分别为50%,30%,20%。不同入市时间的
股民数分别占40%,40%,20%。今在该营业点随机找一股民。
(1)求其有赢利的概率;
(2)若已知其亏损了,问他为新股民的概率有多大?
16.有两组同类产品,第一组有30件,其中有10件为优质品;第二
组有20件,其中有15件为优质品今从两组中任选一组,然后从该组中任
取2次(每次取1件,不放回抽样)。
(1)求第1次取到的是优质品的概率;
(2)在已知第2次取到的是优质品的条件下,求第1次取到的不是
优质品的概率。
17.设一股票(股价以收盘价计)当今天(记为第1天)是涨的情
形下第2天是涨(1个单位),跌(1个单位),平(基本持平)的概率
为 ;当今天是跌(或是平)的情形下上述三种情况发
生的概率分别为 。
即明天的情况只与今天有关。其中。已知该股票今天是涨的。
(1)求第3天与今天持平的概率p1;(2)第4天股价比今天涨了2个单位的概率p2。
18.试证:当O
19.设A,B,C为随机事件,P(A)>0,P(B)>O,P(C)>
0。请说明以下说法对,错或可能对。
(1)A,B相互独立,则A,B相容;
(2)P(A)=0.6,P(B)=0.7,则A,B独立。
(3)P(ABC) =P(A)?P(B)?P(C),则A,B,C相互独
立。
(4)A,B不相容,则A,B不独立
20.由4个独立部件组成的一个系统,第i个部件工作正常的概率为。且已知至少有3个部件工作正常时系统工作正
常。
(1)求系统工作正常的概率α;
(2)在系统工作正常的条件下求4个部件均工作正常的概率β;
(3)对系统独立观察3次,求系统恰有2次工作正常的概率γ。
21.连续抛一枚硬币,p表示每次出现正面的概率,记。求:
(1);
(2) ;
(3) 。
22.已知一批照明用灯管使用寿命大于1000小时的概率为95%,大
于2000小时的概率为30%,大于4000小时的概率为5%。
(1)已知一灯管使用了1000小时没有坏,求其使用寿命大于4000
小时的概率;
(2)取10个灯管独立地装在一大厅内,过了2000小时,求至少有3
个损坏的概率。
23.一系统的外加电压有99%的时间是正常的,当外加电压正常时
系统稳定的概率为90%,当外加电压不正常时系统稳定的概率为20时。
且已知当系统稳定时元件正常工作的概率为80%,当系统不稳定时元件
不能正常工作的概率为90%。
(1)求元件能正常工作的概率;
(2)若该系统有5个独立工作的元件,求至少有一个元件不能正常
工作的概率。第二章 随机变量及其概率分布
§2.1 随机变量
随机试验的结果常有两类:示数的和示性的。例如,观察某一车间
的用电量;观察某一区域一天内发生的交通事故次数;记录一天内一手
机收到的短信数;气象上的温度及相对湿度,等等,其结果均可用一数
来表示。我们称这些试验的结果为“示数的”,但也有大量的随机试验的
结果却不然,例如,抛一枚硬币,其结果可能是正面或反面;记录新生
儿的性别,其结果是男或女;检验一件产品,它可能是一等品、二等
品、等外品,等等,我们称这类试验的结果为“示性的”。为了用更多的
数学方法来描述与研究随机现象,必要时人们常常将示性的结果数量
化,即定义一个实数与示性的结果相对应。
同时,相对于随机试验的实际结果而言,有时我们更感兴趣这些结
果的某些函数,例如,观察某一地区新生儿的性别,我们感兴趣于男
婴、女婴的数量,同时也感兴趣于两者的数量之差。又如,我们观察一
运动体的速度的随机变化,我们还感兴趣于随之产生的运动体的动能的
变化情况。由上面这些例子可以看到,我们感兴趣的量是随机试验的结
果的实值函数,我们称它为随机变量。通俗说,随机变量就是随随机试
验结果而变的量。一般地,有下面的定义。
定义2.1.1 设随机试验的样本空间为S={e},若X=X(e)为定义
在样本空间S上的实值单值函数,则称X=X(e)为随机变量(random
variable)。
如果随机试验的结果是示数的,则样本点e即为一实数,这时常定
义X=X(e)=e。
本书中常用大写英文字母
来表示随机变量,而以小写字母表示实数。
引入了随机变量,一方面使我们能够用随机变量来描述随机现象,另一方面也可以同时用研究随机变量取值的概率来代替随机现象发生的
概率。
例2.1.1 一枚硬币抛4次,设每次出现正面的概率为p(0
1),记X为4次中出现正面的次数,而4次中首次出现正面在第Y次(如
果4次都没有出现正面,则取i=0)。试分别写出X与Y的所有可能取值
与取每一值的概率。
解 首先,易得X与Y的所有可能取值均为:0,1,2,3,4.设。由题意知,。得
Y取每一值的概率分别为:而且,我们可以验算得到。
例2.1.2 某销售员独立地向编号为1,2的两顾客推销售价分别为
17.3万与18.7万的A,B两款小轿车,与这两位顾客成交的概率分别为0.4
与0.7。设每位顾客选择A,B两款车型的概率相等,试给出该销售员的
成交额X的可能取值与取每一值的概率〔假定每位顾客最多买一辆)。
解 由题意知,X的可能取值为:0,17.3,18.7,34.6,36,37.4.
设
由于对编号为1,2的两顾客是独立推销的,因此两位顾客的购买行为是
独立的,也就是说, 都是独立的,同理, 也都是独立的。而且。因此§2.2 离散型随机变量
若随机变量的取值为有限个或可列个,则称此随机变量为离散型
(discrete)随机变量,简称离散量。
例如,§2.1中的例2.1.1与例2.1.2中的随机变量取值均为有限个,故
它们均为离散型随机变量。又如,抛一枚硬币,直到正面首次出现所需
的抛掷次数,一个广场上的人数等等,这些量可能没有上限,但均可
列,所以这些量也是离散型随机变量。若以X记某一地区成年男子的身
高,以Y记某产品的寿命,显然X与Y的取值充满着某一区间,它们的可
能取值不能一一列出,所以X与Y不是离散量。
离散量的统计规律通常用概率分布律来描述。
设X为离散量,若其可能取值为
,则称
为X的概率分布律(distribution sequence)。
概率分布律也可用下面的列表方式来表示:
概率分布律有以下两条性质:。
性质(1)是显然的。性质(2)是因为是不同的样本点,即对
是两两不相容的,这样就得到了性质(2)。
例2.2.1 随机变量X的概率分布律为
求常数c的值。
解 这里先回忆一下高等数学中的一个函数展开式。由概率分布律的性质知,那么 。
以下介绍几个重要的离散量。
(一)0-1(p)分布
若随机变量X的概率分布律为其中,0
用记号X~0-1(p)表示(也可表示为B(1,p))。
例如:若某一地区每一个新生儿是男(或女)的概率为。0.51(或
0.49),记{X=1}为男孩,{X=0}为女孩,则X~0-1(0.51)。
(二)二项分布
若随机变量X的概率分布律为
其中, ,则称X服从参数为(n,p)
的二项(binomial)分布,且记为 。
显然,(2.2.2)式中
,且
在讨论二项分布时必须提到下面的重要试验。
定义2.2.1 在n次独立重复的试验中,每次试验都只有两个结果:,且每次试验中A发生的概率不变,记
,称这一系列试验为n
重贝努里(Bernoulli)试验。
例如,若考虑一个试验的结果只有成功与失败,且每次成功的概率
都为p,O
验.又如,独立重复地抛n次硬币,每次结果只有正面或反面;在一放
有红球与其他颜色的球的袋中有放回地摸球n次,每次只记录摸到红球
与其他球(非红球)两种结果,且设每次摸到红球的概率是p,O
1,等等,都可以看成是n重贝努里试验。
在n重贝努里试验中,若记事件A发生的概率为P(A)=p,O
1。设X为在n次试验中A发生的次数,则X~B(n,p),即
因为事件{X=k}即为“在n次试验中恰有k次A发生且有。n-k次A不发
生”,这k次可以是n次中的任意k次,故有 种方式,而每一“特定
的k次A发生且特定的(n-k)次A不发生”的概率为
,这样就得到了(2.2.2)式。读者可以再
详细地看一下§2.1例2.1.1中随机变量X的概率分布律的求解过程。特别
地,当n=1时,B(1,p)即为。0-1(p)分布。
例2.2.2 由6位品酒师独立投票评定某种酒是否为优质酒,若6位中
有4位投票同意,则定该酒为优质酒,且设每位品酒师作出正确判断的
概率为p,0
(1)若该酒为优质酒时,能作出正确判断的概率α。(2)若该酒
不为优质酒时,能作出正确判断的概率β。
解(1)当该酒为优质酒时,至少要有4位品酒师作出正确判断才能
判定此酒为优质酒,所以(2)当该酒不是优质酒时,则至少要有3位品酒师作出正确判断,所以
例2.2.3 设有一大批优质品率为p的产品,O
进行验收:第一次先从中随机取5件,若至少有4件是优质品则接收该批
产品,若优质品不到3件就拒收;否则再第二次从中抽2件,若2件均为
优质品就接收,否则就拒收。求:(1)第一次抽样就接收该批的概率
α。(2)该批产品被接收的概率β。
解 由题意知,各次抽样结果相互独立(由于是一大批,总的数自
很多)。设X为第一次抽到的优质品数,Y为第二次抽到的优质品数,显
然 。
一般情形下,当n不是很大的时候,对于二项分布的计算还是比较
容易的,但当n比较大的时候,二项分布的概率值可以采用Excel计算。
例2.2.4 假设 ,现分别计算P(X≤10)和P(X=10)。
解 先计算P(X≤10),由二项分布可知:显然这个计算不是很简单,但可以通过Excel表单简单得出。具体如
下:在Excel表单的任一单元格输入 在主菜单中点
击“插入” “函数(F)” 在选择类别的下拉式菜单中选
择“统计” 选择“BINOMDIST”点击”确定” 在函数参数
表单中输入“Number_s=10,Trial=100,Probability_s=0.05,Cumulative=TRUE”,然后点“确定” 即在单元格中出
现“0.98852759”。
如果要计算P(X=10),则只需要在上面的过程中所有的步骤中
把“Cumulative=TRUE”改“Cumulative=FALSE”。即在单元格中出
现“0.016715884”。
(三)泊松分布
若随机变量X的概率分布律为
其中λ>0,则称X服从参数为λ的泊松(Poisson)分布,且记为。
观察(2.2.3),显然有对任意的
,且由§2.2的例2.2.1知,。
参数λ的含义将在第四章中说明,而有关泊松分布的数学模型将在随机过程第十二章中研究。
泊松分布有着非常广泛的应用.这是因为当n足够大,p充分小(一
般要求p<0.1),且np保持适当大小时,参数为(n,p)的二项分布可
用泊松分布近似描述。
设X~B(n,p),并记λ=np。则
当n充分大和适当的λ时,也就是说,当n充分大,p足够小时,根据统计工作者的经验,以下的随机变量常可近似用泊松分布描
述:
1.某产品的不合格点数;
2.一本书一页上的印刷错误数;
3.一手机某一时间段内收到的信息次数;
4.某放射物在一定时间内放射出的α粒子数;
5.一定的时间区间内进入某书亭的人数。例2.2.5 设某公共汽车站单位时间内候车人数X服从参数为4.8的泊
松分布。求;(1)随机观察1单位时间,至少有3个人候车的概率;
(2)随机地独立观察5个单位时间,恰有4个单位时间至少有3人候车的
概率。
解 (1)由题意知,X~π(λ),其中λ=4.8则
(2)设被观察的5个单位时间内有Y个单位时间是“至少有3个人候
车”,则Y~B(5,p),其中p=P{X,≥3}=0.8575。那么
例2.2.6 某地区一个月内每200个成年人中有1个会患上某种疾病,设各人是否患病相互独立。若该地区一社区有1000个成年人,求某月内
该社区至少有3人患病的概率。
解 记p=1200,且设该社区1000人中有X人患病。由题意知,X~
B(1000,p),记λ=1000p=5。利用(2.2.4)式,所要求的概率为
例2.2.7 例2.2.6的计算可以通过Excel表单简单得出。先计算出
P{X≤2}具体如下:在Excel表单的任一单元格输人“=” 在主
菜单中点击“插入” “函数(F)” 在选择类别的下拉式
菜单中选择“统计” 选择“POISSON”点击“确定” 在函
数参数表单中输人“X=2,Mean=5,Cumulative=TRUE”,然后点“确定” 即在单元格中出现“0.124652019”。P{X≥3}=1
-P{X≤2}=0.875347981。
(四)其他离散型随机变量
例2.2.8 一袋中共有N个球,其中有a个白球与b个红球(a+b
=N)。从中不放回地取n(n≤N)个球,设每次取到各球的概率相等。
若其中有X只白球,试写出X的概率分布律。
解 这是一个等可能概型,其中。
如果随机变量X具有形如(2.2.5)的概率分布律,则称X服从超几
何(hypergeometric)分布。
例2.2.9 设独立重复试验中,每次试验有两个结果: 。
每次试验中A出现的概率不变,记P(A)=p,0
发生时所需的试验次数为X,求X的概率分布律。
解 参照§2.1的例2.1.1中求Y的概率分布律的方法,可知
如果随机变量X具有形如(2.2.6)的概率分布律,则称X服从参数
为p的几何(geometric)分布。§2.3 随机变量的概率分布函数
前面我们介绍了离散型随机变量及其概率分布律。但实际上也有许
多随机变量的取值是不可列的,因此就不能用概率分布律来描述其概率
分布规律。例如,打靶时弹着点离开靶心的距离;一地区成年男子的身
高;一批产品的寿命;在职职工个人月收入,等等,这些量均不可列,不是离散量。事实上,我们也不关心这类量取某一定值的概率,而是关
心其落在某些区域的可能性大小。例如,我们可能会关心事件“打了8环
以上”,“身高大于170cm”,“寿命大于1000小时且小于2000小时”,“职
工月收入低于3000元”的概率。下面我们引入概率分布函数的概念。
定义2.3.1 设X为一随机变量,x为任意实数,函数
称为随机变量X的概率分布函数,简称分布函数(distribution
function)。
对任意的实数 ,有
这说明X落在区间 的概率为两端点分布函数值之差。
也就是说,如果X的分布函数F(x)已知,则可以求出事件
的概率。从这个意义上说明,F(x)能完整地描述X的概率分布。
图2.3.1
几何地来看分布函数,将X设想成一随机点,那么X落在区间(-
∞,x]上的概率即为F(x)(如图2.3.1所示)。当X为离散量时,设X的概率分布律为。
则X的分布函数为
即F(x)为满足 的一切xi
的相应的概率之和。
例2.3.1 随机变量X~0-1(p)分布,0
分布函数及其图形;(2)P{X≥1}的值。
解 (1)由题意知,X具有概率分布律
那么X的分布函数为
(2)。
概率分布函数的性质:
(1)F(x)单调不减;这一点由(2.3.2)式即可知,当
,因此 。
(2)0≤F(x)≤1,且有
,简记为F(-∞)=F(+∞)=1。
因为F(x)为事件{X≤x}的概率,所以有0≤F(x)≤l。
又可设想有实数数列
越
小,事件 越来越接近不可能事件,故有F(-
∞)=0。用同样的方式可以理解F(+∞)=1。
(3)F(x+0)=F(x),即F(x)是右连续函数(证略)。
图2.3.2例如本节例2.3.1中的F(x)(见图2.3.2)在x=0,1点上为右连
续,在其他点上均为连续函数。
图2.3.3
例2.3.2 设一醉汉在A,B两点间移动,A,B两点间的距离为3个单
位。A,B两点有障碍物,他停留在A,B两点的概率均为14。设他离
开A的距离为X,且落在A,B两点间任一区间的概率与区间长度成正
比,求X的概率分布函数。
解 由题意知,P{X=0}=P{X=3}=14。
设比例常数为k,则
得k=16。显然有,当:x<0时,F(x)=0;
当x=0时,F(x)=14;当x≥3时,F(x)=l。而当0
接下来我们关注一类重要的非离散型随机变量——连续型随机变
量。
定义2.4.1 对于随机变量X,若存在一个非负的实函数f(x),使X
落在任一区域D上的概率
则称X为连续型随机变量,简称连续量。称f(x)为X的概率密度函数
(probability density function),简称密度。
由定义知,密度函数具有以下性质:
(1)f(x)≥0;
(2) ;
(3)X的概率分布函数;
(4)在f(x)的连续点x处, 。
由(2.4.1)式可知X属于区域D的概率等于概率密度函数在区域D上
的积分。令D=[a,b],则有上式中,若令a=b,则有
即,连续型随机变量取任一定值的概率为零。因此连续量落在开区间与
相应的闭区间上的概率相等。
例2.4.1 设X为连续型随机变量,其密度函数为
求(1)常数c的值;(2)P{X<0.5}的值。
解 (1)由概率密度的性质(2)可知,得c=32。
例2.4.2 一电子产品的无故障工作时间X(以小时计)为连续型随
机变量,其密度函数为求(1)常数λ的值;(2)从大批该种产品中抽取3只,恰有一只无故障
工作时间小于1050小时的概率。
解 (1)由于
,于是可得λ=11000。
(2)注意到
设3只产品中有Y只寿命小于1050小时,由题意知,Y~B(3,0.6321),那么所要求的概率即为
例2.4.3 一银行服务需等待,设等待时间X(以分钟计)的概率密
度为
某人进了银行,且计划等下还要去办另一件事,故打算先等待,如果15
分钟后还是没有等到服务就离开银行,设此人在银行实际等待时间
为Y。(1)求Y的概率分布函数;(2)问Y是离散量吗?Y是连续量
吗?
解 (1)由分布函数的定义知,Y的概率分布函数为显然,当y≤0时,F(y)=0;当y≥15时,F(y)=l;当0
(2)因为Y的取值范围为[0,15],Y的取值不可数,所以Y不是
离散量。又
,即Y取定值15时概率不为零,所以Y亦不是连续量。因此Y是既非离散
又非连续的随机变量。
本教材主要研究离散量与连续量。
下面我们研究几种重要的连续量。
(一)均匀分布
定义2.4.2 设随机变量X具有概率密度
则称X服从区间(a,b)上均匀(uniform)分布,常记为X~U(a,b)。
显然上面的密度函数满足。
根据密度函数的定义,可知X的概率分布函数为
均匀分布密度函数 均匀分布分布函数
图2.4.1
设有实数c,l,满足 ,则有
上式的值与c无关,即X落在区间[a,b]内任一长度为l的子区间的概
率为子区间的长度与(b-a)的比(即几何测度之比),其概率与l成
正比,而且仅依赖于子区间的长度,与子区间的位置没有关系。
例2.4.4 杭州某长途汽车站每天从早上6:00(第一班车)开始,每隔30分钟有一班车发往上海。设王先生在早上6:20过X分钟到站,且
设X服从(0,50)上均匀分布。(1)求王先生候车时间不到15分钟的概率;(2)如果王先生一个月中有两次按此方式独立地去候车,求他
有一次候车不到15分钟,另一次候车大于10分钟的概率。
解 X~U(0,50),由题意知,只有当王先生在图2.4.2中画阴影
的时间区间内到达时,候车时间会小于15分钟,图2.4.2
阴影区间的长度为25,所以
(2)同样可知,如果王先生在6:30以后至6:50之间或7:00至
7:10之间到达车站,则他的候车时间要大于10分钟,所以
设
那么所要求的概率为
(二)正态分布
正态随机变量是概率论与数理统计中最重要的随机变量。
定义2.4.3 设随机变量X具有概率密度其中参数 ,则称X服从参数为(μ,σ)的正态(normal)分布,或简称X为正态量,记为。
其相应的分布函数为
显然,f(x)≥0。下面来证明。
记
,作积分变量变换,令 ,则
于是通过将积分变量变换成极坐标形式,得
这样就得到I=1。
正态密度f(x)具有以下性质:
(1)f(x)关于x=μ对称;
(2) ;
(3) 。
图2.4.3 正态分布概率密度
由图2.4.3所示的密度曲线图可知,X的取值是中间(μ附近)大,两
头(离μ远的地方)小,而且是对称的(关于x=μ)。
人们常称正态变量的参数μ为位置参数,因为μ给出了密度对称轴的
位置及X的取值集中的位置;称σ为尺度参数,因为密度曲线的尺度(图
形的形状)完全由σ决定(却与μ无关)。
σ越大,曲线峰越低,越扁平,X在μ附近取值的概率(即相应的曲
边梯形的面积)越小,即X取值越分散,故σ是反映X取值分散程度的一
个指标量。
特别地,当μ=0,σ=1时,若记这时的正态量为Z,Z~N(0,1),称Z服从标准正态分布(standard normal distribution),其概率
密度为:
标准正态概率密度 标准正态分布函数
图2.4.4
其相应的分布函数为显然标准正态密度关于y轴对称,由此可得,对于任一实数:x>0
同时,当 时,对于任意的实数a,b,a
作积分变量变换,令 ,得
此时的被积函数为标准正态密度,故有
这样将正态变量的概率计算归结为标准正态分布函数值的计算问题。而
这些数值可查本书附表2。
若 ,由(2.4.5),(2.4.6)式可得
当k=1,2,3时,查附表2可得
图2.4.5
可以发现,以上概率值与μ,σ的取值无关(总结在图2.4.5中)。
例2.4.5 用天平称一实际重量为a的物体,天平的读数为随机变量。当σ=0.01时,(1)求读
数与a的误差小于0.005的概率;(2)求读数至少比a多0.0085的概率;
(3)若重复称3次,求3次中恰有1次“读数与a的误差小于0.005”的概
率。
解 (1)由(2.4.6)式,并查附表2,得
(2);
(3)设3次中有Y次“读数与a的误差小于0.005”,则Y~B(3,0.3830),因此
例2.4.6 上例的计算中正态分布的值可以通过Excel表单简单得
出。例如计算P(X-a<0.0085),具体如下:在Excel表单的任一单元
格输人“=” 在主菜单中点击“插入” “函数(F)”
在选择类别的下拉式菜单中选择“统计” 选
择“NORMDIST”点击“确定” 在函数参数表单中输人“X=
0.0085,Mean=0,Standard_dev=0.01,Cumulative=TRUE”,然后
点“确定” 即在单元格中出现“0.802337508”。
例2.4.7 设一天中经过一高速公路某一入口的重型车辆数X近似服
从 ,已知有25%的天数超过400辆,有33%的天数不
到350辆,求μ,σ。
解 已知P{X>400}=0.25,P{X<350}=0.33,查表得
在自然界与社会现象中许多量可用(或近似用)正态量来描述,那
些我们经常可以看到的(自然形成的)沙堆、谷堆、煤堆以及远处的某
些山的轮廓线,常常会让人们联想到正态密度曲线。我们身边的许多
量,如同一年龄段的人的身高,体重(但视力测量值不是正态量);一
个地区某一时段的降雨量;某公司普通职工的收入;医院里许多化验的
指标量等等,一般均可将其视为正态量,在第五章中我们还可以看到正
态量的更多应用。(三)指数分布
定义2.4.4 设随机变量X具有概率密度
其中λ>0,则称X服从参数为λ的指数(exponential)分布,记为X~
E(λ)。
显然有。
其相应的分布函数为
当X~E(λ)时,对任意的 ,我们有
或写成。
若将X看成某电子产品的寿命(以小时计),则(2.4.10)式可解释
为:“在已知产品用了 小时没有坏的条件下,再用t小时不坏”的条件
概率等于这产品“最初使用t小时不坏”的概率。形象地说这产品“忘却”了“已使用 小时”。所以常将(2.4.10)式形象地称作指数分布
的“无记忆性”。
指数分布概率密度
图2.4.6
例2.4.8 设一地段相邻两次交通事故间隔时间(以小时计)X服从
参数λ=16.5的指数分布。(1)求8个小时内没有发生交通事故的概
率;(2)已知已过去的8个小时中没有发生交通事故,求在未来的2小
时内不发生交通事故的概率。
解 (1)X~E(λ),λ=16.5,则
(2)由(2.4.10)式知
有人说指数分布的无记忆性不好理解,但看了例2.4.8(2)中的等
式
后就有点感觉了吧!
例2.4.9 有编号为1,2,3的3个同类设备。已知它们正常运行时间均服从参数为λ的指数分布。现1号,2号设备已在一系统中独立运行,当其中1台损坏时由3号接替运行。求3个设备运行到最后的不是3号设备
的概率。
解 不妨设1号先损坏,由于指数分布具有无记忆性,由3号接替后
开始考虑2号再正常运行t单位时间的概率应与3号正常运行t单位时间的
概率相等,所以得到“运行到最后的不是3号设备”的概率应为12。
(四)其他连续型随机变量
定义2.4.5 设随机变量X具有概率密度
其中参数α>0,β>0,则称X服从参数为(α,β)的Г(Gamma)分
布,记为X~Г(α,β)。
(2.4.11)式中的。特别地,当n为正整数时,有。
定义2.4.6 设随机变量X具有概率密度
其中参数α>0,γ>0,则称X服从参数为(>α,γ)的二参数威布尔
(Weibull)分布。
定义2.4.7 记随机变量X具有概率密度其中参数a>0,b>0,则称X服从参数为(a,b)的β(Beta)分布,记为X~β(a,b)。§2.5 随机变量函数的分布
在实际问题中,我们常会碰到已知一随机变量的分布,要求这一变
量的函数的分布问题。例如,已知到达车站的时间服从某一区间上的均
勾分布,要求候车时间的分布;已知半径测量值为正态分布,要求对应
的圆面积的分布,等等。本节要研究一个随机变量函数的分布问题。即
已知X的分布,Y=g(X),要求Y的分布。下面先来看几个例题。
例2.5.1 抛一枚骰子,当点数不大于3时定义Y=-1,当点数为4或
5时定义Y=0,当点数为6时定义Y=l。且记Z=Y2。(1)求Y的概率分
布律;(2)求Z的概率分布律。
解 (1)设抛一枚骰子得到的点数为X。由题意知当且仅当
{X≤3}发生时{Y=-1}发生,我们称事件{X≤3}与事件{Y=-
1}等价。同理事件{X=4}∪{X=5}与{Y=0}等价,事件{X=
6}与{Y=l)等价。故有
即
(2)由题意知 的可能取值为0,1。与(1)的解
法相同,得例2.5.2 设一商店某一批电子产品使用寿命(以小时计)X~
E(λ),λ=l250。商店对该批产品实行先使用后付款的办法销售。若
使用寿命小于100小时,顾客不用付费;若使用寿命大于100且小于250
小时,顾客得付10元;若使用寿命大于250小时,则要付30元。求顾客
付费的概率分布律。
解 设顾客付费的金额为Y元,Y的可能取值为:0,10,30。由题
意知X~E(λ),λ=1250。由于电子产品使用寿命小于100小时,顾客
不用付费,那么
同理可得
由例2.5.1,例2.5.2可知,若X的分布已知,Y=g(X),且Y为离散
量时,可先列出Y的可能取值…然后找出事件
的等价事件 ,从而求出Y的
分布律 即
可。另外,当Y=g(X)为连续量时,我们总是先找出{Y≤y},即
{g(X)≤y}的等价事件 ,从而求出Y的分布函数。总之,求随机变量函数的分布问题实质上就是找等价事件问题。
例2.5.3 设随机变量X的概率密度为Y=X2
,求Y的概率分布函数 及密度函数。
解 由题意知,当i≤0时,。
当0
例2.5.4 设X的概率密度为。求Y与Z的
概率密度 。
解 设Y与Z的分布函数分别为。当y≤0时,显然有 。当y>0时,有
当t≤0时,显然有 。当t>0时,有
定理2.5.1 设X为一连续型随机变量,其概率密度为
,随机变量Y=g(X),若函数y=g(x)为一严格单调
增函数(或减函数),且可微。记y=g(x)的反函数为x=h(y)。
则Y的概率密度为
其中D为函数y=g(x)的值域。
证明 先设y=g(x)为一严格单调增函数,即g′(x)≥0,注意此
时的h′(y)≥0。而Y的分布函数为从而。
若y=g(x)为一严格单调减函数,即g′(x)≤0,此时并有h′(y)
≤0。故Y的分布函数为
从而。这样就证明了(2.5.1)式。
例2.5.5 随机变量
求Y
的概率密度。
解 记y=g(x)=ax+b,则其反函数为。满足定理2.5.1的条件,故有
即 。特别地当。也就是说一个正态量的线性函数仍为正态量;特别地,当
是标准正态量。
例2.5.6 设连续型随机变量X的分布函数为F(x),且当0<
F(x)<1时F(x)为严格单调函数,记Y=F(X),证明:Y服从区间
(0,1)上的均匀分布。
证明 由分布函数的性质知,0≤F(x)≤l,故Y的取值也属于区间
[0,1]。显然有,当y≤0时,。
当0
即
由 的表示式就知Y~
U(0,1),命题得证。思考题二
1.随机变量与实变量有什么区别?
2.取值充满一区间的量一定是连续量吗?
3.若随机变量X分布律为 ,则X的分布函数是
,对吗?
4.设随机变量X,Y的概率密度分别为
,则以下可作为概率密度的是( )
(A)
(B)
(C)
(D)
5.以下函数中能作为概率分布函数的是6.设 ,对任意的
的值仅与μ有关吗?仅与
σ有关吗?还是与μ,σ都有关?
7.若一元件寿命服从指数分布,由指数分布的无记忆性,是否可
认为这元件永远不会损坏?习题二
1.从1,2,3,4,5,6,7这7个数中随机抽取3个数(不放回抽
样),并将其从小到大排队,设排在中间的数为X,求X的概率分布
律。
2.某电脑小游戏要依次独立地过3关,如果过不了关就结束。并规
定过了第1,2关各得1分,过了第3关记为4分,第1关未过得0分。若设
一玩者每关通过的概率为20%。
(1)写出此人得分数X的概率分布律;
(2)求此人得分数大于2的概率;
(3)已知此人得分不低于2,求此人得4分的概率。
3.某人买一种数字型体育彩票,每一注号码中大奖的概率为10-7。
(1)若每期买1注,共买了n期,求没有中大奖的概率;
(2)若每期买10注(号码全不同),共买了n期,求没有中大奖的
概率。
4.某医院男婴的出生率为0.51,如果在该院随机找3名新生儿,求
(1)至少有1名男婴的概率;
(2)恰有1名男婴的概率;
(3)第1,第2名是男婴,第3名是女婴的概率;
(4)第1,第2名是男婴的概率。
5.一车辆从A地到B地要经过3个特殊地段,经过这3个地段时车辆
发生故障的概率分别为 。设其余地段车辆
不发生事故,且记X为从A地到B地发生的故障数,Y为首次发生故障时已通过的特殊地段数(如没有发生故障,则记Y=3)。试分别写出X,Y的概率分布律。
6.从一批不合格品率为p(0
果查到不合格品就停止检查,且最多查5件产品。设停止时已检查了X件
产品。
(1)求X的概率分布律;
(2)求P{X≤2.5}的值。
7.要诊断可疑病人是否患有某种罕见疾病,常邀请国内5名著名专
家会诊,当至少有3名专家认为其有病时就诊断其有病。设每位专家“有
病诊断为无病”的概率为10%,“无病诊断为有病”的概率为20%,且专
家诊断行为独立。可疑病人有病的概率为70%。
(1)求此人有病的条件下,诊断为有病的概率α及此人无病的条件
下诊断为无病的概率β;
(2)求诊断正确的概率;
(3)此人被诊断为有病的概率。
8.(接第7题)若已知恰有3名专家意见一致,求诊断正确的概
率。
9.某公交车站单位时间内候车人数服从参数为λ的泊松分布。
(1)若已知单位时间内至少有1人候车的概率为
,求单位时间内至少有2人候车的概率;
(2)若λ=3.2,已知我们班有一位同学在那里候车,求这车站就他
1人候车的概率。
10.设某手机在早上9:00至晚上9:00的任一长度为t(分)的时间区间内收到的短信数X服从参数为λt的泊松分布, ,且
与时间起点无关。
(1)求10:00至12:00期间恰好收到6条短信的概率;
(2)已知在10:00至12:00期间至少有5条短信的条件下,求在该
时段恰好收到6条短信的概率。
11.某大学定每年的5月份为教职工进行体检,根据以往的情况
知,通过体检发现 的被检者患有重大疾病。已知有3000人参
加今年的体检,求至少有2人被检出重大疾病的概率(可用泊松分布近
似计算)。
12.设随机变量X具有以下性质:
(1)试写出X的概率分布函数;
(2)求P{X≤2.5}的值。
13.设随机变量X的概率密度为
(1)求常数c的值;
(2)求X的分布函数F(x);
(3)求P{-1
率。
14.已知在早上7:00~8:00有两班车(7:30,7:50)从A校区
到B校区,一学生在7:20~7:45随机到达车站乘这两辆车。
(1)求该学生等车时间小于10分钟的概率;
(2)该学生等车时间大于5分钟又小于15分钟的概率;
(3)已知其候车时间大于5分钟的条件下,求其乘上7:30的班车
的概率。
15.从区间(-1,3)中随机取一数X,试写出X的概率密度函
数;若在该区间随机取n个数,设其中有Y个数大于0,求P{Y=k},k
=0,1,2,…,n的值。
16.设随机变量X服从 ,其中μ=5,σ=1。求:
17.设A君的年收入扣除日常必需的花费后的余额(以万元计)X
服从N(2.3,0.25),且往年没有积蓄,也不打算借贷,今年他计划至
少花3万元买些中高档家电,你说他能实现自己计划的概率有多大?
18.设一地区的青年男子身高(以cm计)X服从N(170,5.02)。
今在这地区随机找一青年男子测身高。求:
(1)身高大于170cm的概率;
(2)身高大于165cm且小于175cm的概率;
(3)身高小于172cm的概率。
19.设系统电压小于200伏,在区间[200,240]伏和超过240伏3
种情况下,系统中某种电子元件不能正常工作的概率分别为0.1,0.001,0.2。设系统电压X服从N(220,252)。(1)求该电子元件不能正常工作的概率α;
(2)该电子元件不能正常工作时,求系统电压超过240伏的概率
β;
(3)若一系统有3个这种元件,且若至少有2只正常时系统运行正
常,求该系统运行正常的概率θ。
20.设随机变量Z服从标准正态分布,对于实数:x0
,若
,则称x0
为标准正态分布的上侧α分
位点,常记 。试用上侧分位点表示满足以下条
件的常数a,b,c,。
21.设随机变量X服从N(15,4),X落在区间
中的概率之比为50:34:16,求 的值。
22.设随机变量X的概率密度为。试求:
(1)常数a的值;(2) 的值。
23.设银行的某一柜台一位顾客的服务时间(以分计)服从参数λ
=18的指数分布,在A到达时恰好有1人先于其到达,设A的等待时间
为X。
(1)写出X的概率密度;
(2)求A等待时间超过10分钟的概率;
(3)求等待时间大于8分钟且小于16分钟的概率。
24.设甲,乙两厂生产的同类型产品寿命(以年计)分别服从参数
为13和16的指数分布,将两厂的产品混在一起,其中甲厂的产品数占
40%。现从这批混合产品中随机取一件产品。
(1)求该产品寿命大于6年的概率;
(2)若已知该产品使用了6年仍未坏,求该产品再使用2年不坏的
概率。
25.以X表示某商店早晨开门后直到第一个顾客到达的等待时间
(以分计),X的概率分布函数为
(1)求X的概率密度函数f(x);
(2)求P{5
(3)求某一周(7天)至少有6天等待时间不超过5分钟的概率。
26.设一批电子元件寿命X(以小时计)的概率密度函数为某人买了3只元件试用。若至少有2只寿命大于150小时,则下次再
买此类元件。求
(1)这3只元件中恰好有2只寿命大于150小时的概率;
(2)这个人会再买的概率。
27.某次游戏向每个玩者发5个球,向目标投掷,投中2次就结束投
球。若每次投中的概率均为p=0.7,且每次投掷是相互独立的。设X为
结束时的投球次数,规定当X=2时得10分,X=3时得8分,X≥4时得2
分,记Y为得分数。试写出Y的概率分布律。
28.已知随机变量X的概率密度函数为
(1)求常数c的值;
(2)设Y=3X,求Y的概率密度;
(3)设Z=|X|,求Z的概率分布函数及概率密度。
29.设在(0,t]时间区间内进入某商店的顾客数N(t)服从参数
为λt的泊松分布,且设先后两个顾客进入的间隔时间为T,(l)求T的概
率分布函数。(2)求
的值,其中 。
30.从区间(0,1)上随机取一数X,记
为自然数),求Y的概率密度。31.设随机变量X服从在 上的均匀分布,Y=
cosX,求Y的概率分布函数。
32.设随机变量
的概率密度。
33.设随机变量X的概率密度为
已知P{X
(1)求常数a,b; (2)设 ,求Y的概率密度
函数 。
34.设随机变量。(1)求Y的概率密度;(2)求Z的概率密度。第三章 多元随机变量及其分布
在第二章中,我们研究了单个随机变量的概率分布问题,但许多随
机现象用一个变量来描述是不够的,例如要预报明天的天气状况,就要
观察与预测许多个随机变量(如:温度、湿度、风力,等等)的变化情
况,又比如要制定一地区成年男子衬衣(大、中、小号的尺寸)标准,就需要研究这些人的衣长、袖长、领围、肩宽、胸围,等等随机变量以
及这些量之间的关系。所以研究多元随机变量是必需的。本教材将较深
入地研究二元随机变量,可能时可以将这些方法用于研究多元随机变
量。
设一随机试验E,其样本空间为S={e),定义随机变量X=
X(e),Y=Y(e),称向量(X,Y)为二元随机向量或称二元随机变
量。§3.1 二元离散型随机变量
定义3.1.1 若二元随机变量(X,Y)的取值有限或可列,则称
(X,Y)为二元离散型随机变量或称二元离散量。
(一)二元离散量的联合分布
设二元离散量(X,Y)的可能取值为
,与一元离散量相
似,称
为(X,Y)的联合概率分布律或简称联合分布律。上式亦可用列表的
方式表示。
联合分布律满足。
由概率的性质知(1)成立,又
是样本点,所以两两不相容,且其全体构成一样本空间,故(2)亦成
立。
例3.1.1 一袋中有5个白球,1个红球和2个黑球。每次摸1球,不放
回抽样3次。设3次中有X次摸到白球,Y次摸到红球,求(X,Y)的联
合概率分布律。
解 由题意知,X的可能取值为0,1,2,3,Y的可能取值为0,1。记 ,则
(下式中 即为组合数 )
(二)二元离散量的边际分布
设二元离散量(X,Y)的联合分布律为
,故有
同样可得
注:符号“ ”表示“记为”。
显然有,,即(3.1.2)及(3.1.3)满足分布律的性质,它们分别是随机变量X与Y
的概率分布律,分别称为关于X及关于Y的边际分布律或边缘分布律。
用列表的方法来表示联合及边际分布更能理解其字面的意义。
上表内第i行(或第j列)累计后记作 ,上表列
在联合分布律表的边上的这一列(或一行)恰是X(或Y)的分布律,故
称其为边际分布律。
例3.1.2 设一群体80%人不吸烟,有15%的人少量吸烟,5%的人
吸烟较多,且已知近期他们患呼吸道疾病(以下简称患病)的概率分别
为5%,25%,70%。记求:(1)(X,Y)的联合分布与边际分布;(2)求患病人中吸烟的概
率。
解 (1)记。由题意知,X的边际分布律为
(2)要求的概率为
即患病的人中有近65%的人吸烟。
(三)二元离散量的条件分布
从上面的例3.1.2(2)可以看到,研究二元离散量的条件概率是有趣和必要的。下面我们就来研究一下二元离散量的条件分布问题。
设二元离散量(X,Y)的联合分布律为
,则当 时,同理可得,当 时,称(3.1.4)(或(3.1.5))式为给定
的条件下X(或Y)的
条件分布律。
(3.1.4)式中显然有。同样,(3.1.5)式中有。亦即(3.1.4)及(3.1.5)式满足分布律的
性质。例3.1.3 设二元离散量(X,Y)的联合概率分布律为
且已知 求:
(1)a,b的值;(2){X=2}的条件下Y的条件分布律;(3){X
+Y=2}的条件下X的条件分布律。
解 (1)。由联合分布律的性质知,a+b+0.6=1,得b=0.4。
(2)P{X=2}=0.1+0.1+b=0.6。那么{X=2}的条件下Y的条
件分布律为
也可以写为(3)P{X+Y=2}=P{X=2,Y=0}+P{X=1,Y=1}=
0.3,那么
例3.1.4 设一单位送客车上车人数X服从参数为λ的泊松分布,每个
人行动独立,每个上车人在中途下车(没有坐到终点站)的概率为p,0
合分布律,X与Y的边际分布律以及条件分布律。
解 已知。且由题意知,当m=0,1,2,…时,即 。例3.1.5 一种叫“排列3”的彩票:每次从0~9这10个数中随机取一
个数,共取3次,得3个数的一个排列作为一期彩票的大奖号码。王先生
每一期去买10个不同排列的号码。设X为他首次中大奖时已买的彩票期
数,Y表示第2次中大奖已买彩票的期数。(1)求(X,Y)的联合分布
律;(2)已知他买了100期时第2次中大奖,求X的条件分布律。
解 (1)由题意知,每一个号码中大奖的概率为1103。买10个不
同号码,中大奖的概率为1100。记p=1100。
设Ai
={王先生买了第i期彩票中大奖},i=1,2,…则
即当已知王先生在买了100期彩票时第2次中大奖,则第1次中大奖在前
99期中是等可能的。§3.2 二元随机变量的分布函数
在§3.1中我们研究了二元离散型随机变量的联合分布律,边际分布
律与条件分布律。对二元随机变量的分布函数,我们同样要研究这三方
面的内容。
(一)二元随机变量的联合分布函数
定义3.2.1 设二元随机变量(X,Y),对于任意的实数x,y,称函
数
图3.2.1
为(X,Y)的联合分布函数。
若将(x,y)看作随机点的坐标,则分布函数F(x,y)即为(x,y)落在图3.2.1阴影部分区域的概率。
与一元随机变量的分布函数一样,相应地,F(x,y)具有以下性
质:
(1)当给定 关于y单调不减;当给定 关于x单调
不减。
(2)。
(3)
关于x右连续,关于y右连续。(证略)
(4)当实数 时,性质(1),(2)可参照一元变量的分布函数相应性质的证明方法
进行证明。
为了证明性质(4),设。易知。从而(二)二元随机变量的边际(边缘)分布函数
在§3.1中我们称单个变量的概率分布律为边际分布律,在此我们同
样称单个随机变量的分布函数为边际分布函数。
记二元变量(X,Y)的联合分布函数为F(x,y),X,Y的边际分
布函数为 ,则
同理, 。即,二元随
机变量的边际分布函数是联合分布函数当另一个变量趋向于+∞时的极
限函数。
以后我们不一一说明地常用 表
示X,Y的边际分布函数,用F(x,y)表示(X,Y)的联合分布函数。
(三)条件分布函数
设(x,y)为二元离散量,当
时,称函数
为 条件下Y的条件分布函数。
设(X,Y)为二元连续量(下一节介绍),当任意固定
时,称函数为{X=x}条件下Y的条件分布函数。
条件分布函数具有分布函数的所有性质。
例3.2.1 一袋中有a个白球,b个红球,记a+b=n。每次从袋中任
取一球,不放回抽样,设
(1)试写出 的联合分布函数
的边际分布函数
写出
当 的条件分布函数 。
解 记。由第一
章的例1.3.2,可知。
当,因此
于是可得 的联合分布律如下:(记N
=n(n-1))
那么 的联合分布函数F(x,y)为
(2) 有两种求法。方法一,由 的边际分布律求 ;方法二,可由。现采用方法二。
(3)由 的联合分布律可知,在
的条件下, 的条件分布律为
所以所要求的条件分布函数为§3.1 二元连续型随机变量
(一)二元连续量的联合分布
定义3.3.1 设(X,Y)为二元随机变量,若存在二元函数f(x,y)≥0,对任意的二维空间的集合D,有
则称(X,Y)为二元连续型随机变量,简称二元连续量。称f(x,y)
为(X,Y)的联合概率密度,简称联合密度。
f(x,y)具有以下性质:(其中F(x,y)为(X,Y)的联合分布
函数)
(4)在f(x,y)的连续点上有
由连续量的定义可知,二元连续量(X,Y)落在一面积测度为零的
区域上的概率为零,特别地落在一条曲线上的概率为零。
由f(x,y)的性质(4)知,在f(x,y)的连续点处有这表明(X,Y)的联合密度为(X,Y)落入矩形区域
的概率
与该区域面积之比,当 时的极限值,这与
物理量质量面密度是相通的。且当 充分小时,可得
即(X,Y)落在矩形区域D上的概率近似等于
,同时也表明f(x,y)是描述二元
变量(X,Y)落在点(x,y)附近的概率大小的一个量。
例3.3.1 设二元随机变量(X,Y)的联合概率密度为
其中。(1)求常数c;(2)求(X,Y)的联合分布函数;(3)求。
解 (1)由联合概率密度性质(3)可知
得c=15。
图3.3.1
(2)
,那么显然当x≤0或y≤0时,F(x,y)=0;当x≥1且y≥1时,F(x,y)
=1。
图3.3.2
当 (如图3.3.2)时,
图3.3.3
当 (如图3.3.3)时,同理可得,当0
(3)记
,则
亦可,(二)二元连续量的边际分布设(X,Y)为二元连续量,F(x,y),f(x,y)分别为(X,Y)
的联合分布函数及联合密度函数,称单个随机变量X(或Y)的密度函数
为X(或Y的边际密度函数,且常分别用
表示。由于
那么由连续型随机变量的定义知,X为连续量,且X的概率密度函数为
即边际密度为联合密度关于另一个变量在(-∞,+∞)上的积分。
例3.3.2 设二元随机变量(X,Y)的联合概率密度为
(1)求P{X+Y≥1}的值;(2)求X的边际密度 ;
(3)求P{X>l4}的值。
解 (1)由题意得,(2)当 时,当 。
(3)由题意得,(三)二元连续量的条件分布
图3.3.4
设(X,Y)为二元连续量,由条件分布函数的定义知,在一定的条件下,,且
因此我们有下面的定义:
定义3.3.2 设(X,Y)为二元连续量,f(x,y)为(X,Y)的联
合密度函数, 为X,Y的边际密度函
数。给定{X=x}的条件下,Y的条件密度函数为同样有
条件密度具有以下性质:(以 为例)
(4)给定x,当 在y处连续时,以后,我们不一一说明地常用f(x,y)表示(X,Y)的联合密
度,用 分别表示X,Y的边际密度。
例3.3.3 设有一件事需甲,乙两人先后接力完成,完成时间要求不
能超过30分钟。先由甲工作,再由乙接着干。设甲干了X(分钟),甲,乙两人共干了Y分钟,且设X服从(0,30)的均匀分布,Y服从
(X,30)的均匀分布。(1)求(X,Y)的联合密度;(2)求条件密
度 ;(3)当已知花了25分钟完成此事,求甲干
的时间不超过10分钟的概率。
解 由题意知,X~U(0,30),即由题意知,当甲干了x分钟结束时,Y服从(x,30)的均匀分布,故有,当0
30时,由(3.3.4)知,(2)由于
,所以当0
因此,当0
下面介绍两个重要的连续量。
定义3.3.3 设二元随机变量(X,Y)在二维有界区域D上取值,且
具有联合概率密度
则称(X,Y)服从D上均匀分布。
若D1
是D的一个子集,则可得到
定义3.3.4 设二元随机变量(X,Y)具有联合概率密度(式中其中
,则称(X,Y)服从参数为 的二元
正态分布,记为。
例3.3.4 设二元随机变量(X,Y)在
上均匀分布。(1)求关于X,Y的边际密度;(2)求给定X=x(0
条件下Y的条件密度;(3)求P{Y≤X}的值。
解 (1)因为(X,Y)在D上均勾分布,故(X,Y)具有联合密
度为
又 ,那么显
然,当x≤0或x≥1时,时,即
(2)当0
图3.3.5
(3)由图3.3.5知,,其中。D1
的面积 ,D的面积 ,故。
例3.3.5 设二元随机变量(X,Y)服从
分布。(1)求关于X,Y的边际
密度 ;(2)求条件密度。
解 (1)记 ,则
作积分变量变换,令
,则即 。同理可得。
(2)根据条件密度的定义,知
同理可得
即当 时,X,Y的
边际分布也是正态分布,。当给定X
=x的条件下,Y的条件分布亦为正态分布,此时Y服从。当给定Y
=y时,X的条件分布为。§3.4 随机变量的独立性
先回忆一下,在第一章中,两随机事件A,B独立的定义:当
时,称A,B相互独立。对于两个随机变量X,Y,有下面定义:
定义3.4.1对于任意两个实数集合 ,有
则称随机变量X,Y相互独立,简称X,Y独立。
利用概率的三条公理可知,当且仅当对任意实数x,y,有
即为 时
X,Y相互独立。 (3.4.2)
也就是说“对于任意的实数(x,y),(X,Y)的联合分布函数
F(x,y)都等于X与Y的边际分布函数
的乘积”可以作为变量x与Y独立的
等价定义。
特别地,当(X,Y)为二元离散量时,设X,Y的可能取值为
,X与Y相互独立的定
义等价于:对于任意的实数 ,都有当(X,Y)为二元连续量时,由(3.4.2)式得,对于任意的实数
x,y,有
由微积分知识知,两边积分处处相等,被积函数不一定要处处相等,即
可以在面积为零的区域不相等。也就是说,被积函数除了面积为零的区
域外处处相等,这种相等,我们称为几乎处处相等,即
几乎处处成立为连续量X,Y相互独立的等价定义。
当(X,Y)为二元离散量时,由(3.4.3)知,若存在
使得
,则X与Y不独立;当
(X,Y)为二元连续量时,若存在一个面积不为零的区域D0
,使得
,则X与Y亦不独立。
由(3.4.1)式可知,对任意集合
时,X,Y独立的定义亦可写成
由独立的定义知,§3.1的例3.1.2中X与Y不独立。因为
也就是吸烟的多少与患呼吸道疾病是有关的,不独立的。再如§3.3的例3.3.4中的X,Y亦不独立,因为当0
特别地,若(X,Y)为二元正态量,由本章§3.3例3.3.5知,X与Y相
互独立的充分必要条件为ρ=0。因为当且仅当ρ=0时,(3.4.4)式成
立。
在实际问题中,当一个变量的取值不影响另一个变量取任何值的概
率时,常认为这两个变量独立。
图3.4.1
例3.4.1 设在a地与B地间的距离(以公里计)为l(l>1)的公路上
有一辆急修车,急修车所在的位置是随机的。行使中的车辆抛锚地点也
是随机的。求急修车与抛锚车的距离小于0.5公里的概率。
解 设急修车离A地的距离为X,抛锚车离A地的距离为Y。由题意
知,x与y独立,且均在(0,l)上均勾分布。所要求的概率为
定理3.4.1 二元连续量X,Y相互独立的充要条件是X,Y的联合密
度f(x,y)几乎处处可写成x的函数m(x)与y的函数n(y)的乘积,即证明 先证必要性。当X,Y独立时,由(3.4.4)式知,下式几乎
处处成立
记。
再证充分性。当
时,由密度函
数的性质知
记
,那么ab=1。再结合边际密度与联合密度函数的关系,可得
同理得, 。所以
那么由(3.4.4)式知X,Y相互独立。
例3.4.2 问在下面两种情况下,X与Y独立吗?
(1)设(X,Y)的联合密度为(2)设(X,Y)的联合密度为
解 (1)记
故X,Y独立。
(2)由于f(x,y)不能分解成x的函数与y的函数的乘积,故X,Y
不独立。从另一角度来看,我们可以求得X,Y的边际密度分别为
故当。那么由(3.4.4)知,也可知X,Y不独立。
以上关于二元随机变量的一些概念,容易推广到n元随机变量的情
形。
例如:联合分布函数的概念,n元随机变量的联合分布函数为
其中 为任意的实数。
关于边际分布函数,以下举例说明,其他情形可举一反三。例如:
当n>2时,有 的联合边际分布函数
类似地,也可以定义n元离散量与n元连续量。当
的取值至多可列时,称
为n元离散量;若对任意n维
空间的集合D,存在非负函数
,使得
成立,则称 为n元的
连续型随机变量,简称n元连续量,其中的
称之为
的联合概率密度。关于边际概率密度,类似地有,例如:
等等。
若对于任意的实数集 ,有
则称 相互独立。
也即对任意的实数
,有
则称 相互独立。
当 为n元离散量时,亦有如
(3.4.3)类似的独立的等价定义,当
为n元连续量时,亦有如(3.4.4)式相类似的独立的等
价定义。定义3.4.2 设
分别为m元,n元的随机变量,分别用
记它们的联合分布函数。再记
的联合分布函数。
对任意的实数
,若有
则称两向量组
相互独立。
例3.4.3 在n次独立重复的试验中,设每次试验有4个结果:。且每次试验 发生的概率不
变。设。再设在n次试验中 发生的值;(2)在给定 的条件下求
的条件分布律;(3)在给定
的条件下求 的条件
分布律。
解 (1)与n重贝努里试验及二项分布的讨论一样,可知事件
共有n!(n1!n2!n3!n4!)种方式数。而每个Ai
在确定的ni
次发生的概
率为 ,故有
(2)由题知
上面运算用到等式
所以 。故当n1
=0,1,…,n时,(3)先求(X1
,X2)的边际分布
那么当 时,即当给定 的条件下,X3
的
条件分布为。
例3.4.4 一咨询台有A,B两个窗口,设每个顾客服务时间服从参
数为λ的指数分布。有一天一开门,A窗口有一个人要求服务。B窗口有
两人排队要求服务,设每人服务时间相互独立,求B窗口两人先于A窗口1人结束服务的概率。
解 设A窗口一人的服务时间为X1
,B窗口的两个人的服务时间分别
为X2
,X3
,由题意知,X1
,X2
,X3
相互独立。所要求的概率即为
其中, 的联合密度,由题意知,§3.5 二元随机变量函数的分布
在第二章的§2.5中我们研究了一元随机变量的函数的分布问题,并
提到了求一元随机变量函数的分布问题实质是找等价事件。其实求二元
随机变量函数的分布问题实质上也是寻找等价事件。当然求二元随机变
量函数的分布问题较为复杂,下面我们将对一些特殊的形式进行详细的
讨论。
(一)Z=X+Y的分布
在这一部分中,我们将研究已知二元随机变量(X,Y)的概率分
布,求Z=X+Y的概率分布问题。
若(X,Y)为二元离散量,设
,设Z的可能取值为z1
,z2
,…,zk
,…,则显然有
特别地,当X与Y相互独立时,(3.5.1)与(3.5.2)式就可写成
若(X,Y)为二元连续量,设(X,Y)的联合密度为f(x,y),则Z的概率分布函数为作积分变量变换
图3.4.2
这样的变换下可知dxdy=dudv,所以
从而,若作的积分变换为 ,通过同样的计算可得
特别地,当X,Y相互独立时,(3.5.5)式与(3.5.6)式就可写成
例3.5.1 设X~π(λ1),Y~π(λ2),X,Y相互独立。若Z=X+Y,求Z的概率分布律。
解 由题意知,即Z~π(λ1
+λ2)。也就是说,两个独立的泊松分布的随机变量的和仍
服从泊松分布,其参数为两个随机变量的参数之和。
用数学归纳法可以证明:n个独立的服从泊松分布的随机变量的和
仍服从泊松分布,其参数为n个变量的参数之和。
例3.5.2 设
,X,Y独立,Z=X+Y,求Z的概率密度。
对上式积分作积分变量变换,令u=x-t(l+σ2),可知du=dx,从而
可知,此积分值为与t无关的常数,暂且记作a,得
有上式可知 。若当
,X,Y独立时,由例2.5.5知
,由例3.5.2知
再由例2.5.5可得。
用数学归纳法可证,n个独立的正态量之和仍为正态量。
即若,X1
,X2
,…,Xn
独立,且。
进一步可以证明:n个独立的正态量的线性组合仍为正态量。
例3.5.3 设某服务台顾客等待时间(以分计)X服从参数为λ的指数分布,接受服务的时间Y服从(0,20)上的均匀分布,且设X,Y独
立。记顾客在服务台的总时间为Z,即Z=X+Y。(1)求Z的概率密度
函数fZ
(t);(2)设λ=l20,求总时间不超过45分钟的概率。
解 由题意知,因为X,Y独立,所以X,Y的联合概率密度为
方法一:利用(3.5.5)式,
图3.5.1由图3.5.1知,当t≤0时,FZ
(t)=0;
当0
当t≥20时,。
图3.5.2
方法二:可先求Z的分布函数,再求FZ
(t)。由于FZ
(t)=P{X
+Y≤t},由图3.5.2知,当t≤0时FZ
(t)=0。
当0
(2)方法一:利用(1)中的方法二求出FZ
(t)可知,当λ=l20
时,方法二:可由Z的密度函数来计算得到:
例3.5.4 设二元随机变量(X,Y)的联合概率密度为
图3.5.3解 由(3.5.5)式可知
,而且
由(X,Y)的联合概率密度及定理3.4.1知,X,Y不独立,且
显然,当t≤0或t≥2时,fZ
(t)=0;
例3.5.5 某人一天做两份工作,一份工作得到的酬金X具有概率分
布律 ,另一份工作的酬金Y服从N(15,4)。设X,Y独立,记一天酬金总数为Z,Z=X+Y。(1)求Z的概率密
度;(2)求一天酬金多于30的概率。
解 (1)先求Z的概率分布函数,利用全概率公式
因为X与Y独立,故有(2)我们有
(二)M=max(X,Y),N=min(X,Y)的分布
记X,Y的联合分布函数为F(x,y),且记FX
(t),FY
(t)分别
为X,Y的分布函数。
先来讨论M的分布函数,由M的定义可知
特别地,当X与Y独立时,再讨论N的分布函数
特别地,当X与Y独立时,以上结果容易推广到n个变量的情形。特别地,设X1
,X2
,…,Xn
为n个
相互独立的随机变量,相应的分布函数分别为F1
(x1),F2(x2),…,Fn
(xn),记M=max(X1
,X2
,…,Xn),N=min(X1
,X2
,…,Xn),则有例3.5.6 一批元件的寿命服从参数为λ的指数分布,从中随机地取4
件,其寿命记为X1
,X2
,X3
,X4
,由于是随机抽取,故这4个元件的寿命
相互独立。记。(1)求N,M的概率分布函数及概率密度函
数;(2)将4个元件如图连接成一系统,求系统寿命大于t0
(t0
>0)的
概率。
图3.5.4
解 (1)由于X1
,X2
,X3
,X4
相互独立且均服从参数为λ的指数分
布,故当t>0时,(2)设系统寿命为T,则T=min[max(X1
,X2),X3
,X4
],那么
对t0
>而言,有思考题三
1.若已知二元随机变量(X,Y)的联合概率分布就决定了X及Y的
边际概率分布;反之,若已知X及Y的边际概率分布就可决定(X,Y)
的联合概率分布,对吗?若不对,请给出正确的说法。
2.设随机变量X与Y同分布,则以下说法正确吗?
(1)P{X=Y}=l;
(2)P{X+Y=2X}=1;
(3)X与Y有相同的概率分布函数;
(4)X与Y可以有不同的概率分布函数。
3.设二元连续量(X,Y)的联合概率密度为
则(X,Y)的联合分布函数为
对吗?
4.设(X,Y)为二元连续量,则以下等式正确吗?(1) ;
(2) ;
(3);
(4)。
5.当(X,Y)为二元离散量时,若存在点(x0
,y0)使
,则X与Y不独立,对吗?当(X,Y)为二元连续量时,若存在一点
(x0
,y0)使
,则X与Y不独立,对吗?习题三
1.有两个口袋均放着3个红球,2个白球,今从两口袋中同时摸出1
球互换(设每个口袋摸到每个球的概率相等)。记X,Y分别为两袋中互
换球后的红球数,求(X,Y)的联合分布律及关于X的边际分布律。
2.设二元随机变量(X,Y)的联合概率分布律为
且已知事件{X=0}与事件{X+Y=1}相互独立,求常数a,b的值。
3.设二元随机变量(X,Y)的联合概率分布律为
已知P{Y≤0|X<2}=0.5,及P{Y=l}=0.5,求a,b,c的值及X,Y
的边际分布律。4.设随机变量X,Y的概率分布律分别为且已知P{X=0,Y=0}=P{X=1,Y=1}=0.1。
(1)试写出(X,Y)的联合概率分布律;
(2)写出在{X=0}的条件下Y的条件分布律。
5.将一枚均匀的硬币抛3次,记X为3次中正面的次数,Y为3次中正
面次数与反面次数之差的绝对值。
(1)求(X,Y)的联合分布律及边际分布律;
(2)写出{Y=l}的条件下X的条件分布律。
6.某公司出钱为职工订报,每位职工可以从A,B,C3份报中任订
一份,已知有23的女职工决定订A报,有35的男职工决定订B报,余下
的人在3份报中随机选一份。公司男、女职工各占一半。从该公司中随
机找一职工,记
(1)试写出(X,Y)的联合概率分布律;
(2)求Y的边际分布律;
(3)求{Y=l}的条件下,X的条件分布律。
7.设某路段单位时间内发生的交通事故数X服从参数为λ的泊松分
布,其中因超速引起的占总事故数的10%。设因超速引发的事故数
为Y。
(1)求(X,Y)的联合分布律;
(2)求Y的边际分布律。
8.设一大型设备单位时间内发生的故障数X具有概率分布律每次故障以概率p带来损失a(万元)。设Y为该设备在单位时间内的损
失(以万元计)。
(1)求(X,Y)的联合分布律;
(2)已知发生了1次故障,求Y的条件分布律。
9.已知二元随机变量(X,Y)的联合分布函数为
(1)求(X,Y)的边际分布函数FX
(x),FY
(y);
(2)求关于X,Y的边际分布律;
(3)求(X,Y)的联合分布律。
10.设A,B为两随机事件,已知。引入随机变量X,Y,分别为
(1)求(X,Y)的联合分布律;(2)求(X,Y)的联合分布函数;
11.在第10题中,若已知{X=l}的条件下求Y的条件分布函数。
12.设(X,Y)为二元随机变量,已知P{X=0,Y=0}=P{X=
l,Y=l}=0.1,且知(X,Y)落在D={(x,y):0
1}的任一小区域内的概率与该小区域面积成正比,求(X,Y)的联合
分布函数。
13.设二元随机变量(X,Y)的联合概率密度为
(1)求常数c;
(2)求P{X+Y≤1}的值;
(3)求P{X<0.5}的值。
14.二元随机变量(X,Y)的联合概率密度为
(1)求常数c的值;
(2)求X,Y的边际概率密度fX
(x),FY
(y)。
15.二元随机变量(X,Y)的联合概率密度为
(1)求的边际概率密度fX
(x),FY
(y);
(2)求条件概率密度函数fY|X
(y|x);(3)当已知{X=x}时,问Y的条件分布是均匀分布吗?为什么?
16.设(X,Y)为二元随机变量,X的概率密度为
其中λ>0。当:x>0时,Y的条件密度为
(1)求(X,Y)的联合概率密度;
(2)求当x>0时,在给定{X=x}的条件下Y的条件分布函数;
(3)求P{Y>1|X=1}的值。
17.设二元随机变量(X,Y)的联合概率密度为
(1)求Y的边际概率密度fY
(y);
(2)求条件概率密度函数fX|Y
(x|y);
(3)计算 的值。
18.在区间(0,1)上随机取一数X,再在区间(X,l)上随机取
一数Y。(1)求(X,Y)的联合概率密度;
(2)求已知{Y=y}(0
19.在A地至B地(长为m公里)的公路上,事故发生地在离A地X公
里处,事故处理车在离A地Y公里处,X与Y均服从(0,m)上均匀分
布,且设X与Y独立。求事故车与处理车的距离Z的概率密度函教。
20.在半圆
内随机投点A,设A点的坐标为(X,Y)。
(1)求Y的边际密度fY
(y);
(2)求P{Y
(3)X与Y独立吗?为什么?
21.设二元随机变量(X,Y)服从。
(1)试写X,Y的边际概率密度;
(2)写出在{X=0}的条件下Y的条件概率密度;
(3)求P{Y≤1|X=0}的值。
22.设二元随机变量(X,Y)的联合概率密度为
其中f1
(x,y)与f2
(x,y)分别为二元正态变量(X1
,Y1)与(X2
,Y2)的概率密度,且已知(Xi
,Yi)(i=1,2)的边际分布均为标准正态分
布。
(1)求X,Y的边际概率密度fX
(x),fY
(y);
(2)问当(Xi
,Yi)的分布中的参数ρi
=0(i=1,2)时,X与Y独
立吗?
23.一设备由3个独立工作的子系统组成,若其中至少有2个子系统
正常工作时设备就能正常工作。各系统正常工作时间记为X1
,X2
,X3
,且均服从参数为λ的指数分布。求该设备正常工作时间的概率分布函数
及概率密度函数。
24.(1)设随机变量X1
,X2
,…,Xn
独立且均服从参数为p(0
<1)的0-1分布,记 ,求Z的概率分布律。
(2)设X~B(m,p),Y~B(n,p),X与Y相互独立。记W=X
+Y,求W的概率分布律。
25.设随机变量X在区间(-a,a)均匀分布,其中
,X与Y独立,Z=X+Y,求Z的
概率密度。
26.设二元随机变量(X,Y)的联合概率密度为
若Z=X+Y,求Z的概率密度。
27.设有一煤矿一天的产煤量X(以万吨计)服从N(l.5,0.12)分
布。设每天产量相互独立,一个月按30天计,求一月总产量超46万吨的
概率。28.某人连续参加2场比赛,第1,2场比赛可得的奖金数分别为X,Y,且已知 ,Y具有概率密度f(y),X与Y
相互独立。求此人奖金总数Z的概率密度。
29.设一本书一页的错误个数X服从参数为λ的泊松分布,且各页错
误数相互独立。现随机选10页,其错误数分别记为X1
,X2
,…,X10。
(1)求 的值;
(2)求 的值;
(3)求
的值;
30.设随机变量X,Y相互独立,且具有以下分布律
记Z=X+Y,M=max(X,Y),N=min(X,Y),分别求Z,M,N的概率分布律。
31.设一系统由2个独立的子系统组成,分别以X,Y记两个子系统的正常工作时间,且设X,Y分别服从参数为λ1
与λ2
的指数分布。当这2个
子系统分别(1)串联,(2)并联,(3)有备份(当一个损坏时另一
个接着工作)时,分别求系统正常工作时间T的概率密度函数。
32.设二元随机变量(X,Y)的联合概率密度为
记Z=2X-Y,求Z的概率密度。
33.设随机变量X与Y独立同分布,分布律均为。定义
(1)对X独立观察n次,求n次观察值之和W的概率分布律;
(2)求(X,Z)的联合概率分布律。
34.在区间(0,1)上随机取两数X,Y,记Z=XY,求Z的概率分
布函数及概率密度函数。第四章 随机变量的数字特征
在本章的开头,我们先来看一些来自我国官方的数据。
2010年7月16日,国家统计局发布的信息中有以下内容:2009年
(我国)城镇非私营单位在岗职工年平均工资为32736元(2008年为
29229元),城镇私营单位就业人员年均工资为18199元(2008年为
17071元);由上海市统计局发布的信息知,2009年上海城镇居民人均
住房建筑面积为34m2;由杭州市疾控中心发布的信息知,2009年杭州市
居民(大杭州范围,包括区县市)平均期望寿命为80.26岁(即按2009
年的死亡水平,预测2009年出生的孩子。平均可活80.26岁),其中男
性平均期望寿命为77.98岁,女性为82.76岁;国家统计局每个月公布的
居民消费价格指数——CPI(Consumer Price Index),工业品出厂价格
指数——PPI(Producer Price Index)等等。从报纸、电视、网络上我们
能够不断地得到各种各样的信息数据,这些数据是人们根据需要而定义
的。这些数据会影响政府的决策、投资的策略、股票期货市场的波动等
等,甚至引起全世界的关注。因为这些数据浓縮了许多信息,高度集中
地反映了当今社会的某一方面的特性。
从概率统计理论的角度看,职工工资、居民的住房面积、人的寿
命、居民的消费量、工业品出厂价格等都是随机变量,看来有时人们常
常会忽略其概率分布而重视一些能反映其特性的数据(指标量)。简单
地说,称那些能反映随机变量特性的量为随机变量的数字特征或特征
数。实际问题中常用样本数据来分析研究特征数(这要到后面的数理统
计部分讨论)。本章将介绍一元随机变量的数学期望、方差、变异系
数、分位数,以及多元随机变量的协方差、相关系数等常用数字特征。§4.1 数学期望
(一)数学期望的定义
随机变量的数学期望又称为平均数,在介绍其定义之前,我们先看
一个例子:
设抛一颗骰子所得的点数为X,独立重复地抛50次,若观察到为1,2,…,6点的次数分别为8,9,6,8,9,10次,则平均点数为
也就是说,平均值 是X的取值与相应事件的频率的乘积之和。
由§1.2节概率的统计定义知,频率的稳定值定义为概率。因此对于
离散型的随机变量我们有以下定义。
定义4.1.1 设离散型随机变量X的分布律为
若级数 绝对收敛(即),则称级数 为X的数学期望,记为E(X),即其中E是英文expectation的第一个字母。若
,则称随机变量X(等价地,相应的分布)的数学期望不存在。
数学期望的存在需要级数 绝对收敛,这是因为若该
级数不是绝对收敛,而仅仅是条件收敛,此时级数的和会随着级数各项
的排列次序不同而发生改变,从而无法得到唯一的和值。而从直观意义
上来看,离散型随机变量的平均值也应当与分布律中的各项排列次序无
关。
例4.1.1 一种常见的赌博游戏,抛一颗骰子,抛之前让赌客猜结果
为几点,凡猜中者以1:5得奖金,而且规定不管猜中与否押金均归庄家
所有,问此规则对谁有利。
解 不妨假设赌客每次押10元钱,设所得的奖金数为X,据规则他
得50元奖金的概率为16,血本无归的概率为56,因此他赌一次期望能
得到的奖金数为
因此这显然对庄家有利。(试想:否则赌场的开销与高额的利润从何而
来。)
从例4.1.1我们也可体会到“数学期望”这词的含义。
类似地,根据连续型随机变量的定义及积分与级数的关系,对于连
续型随机变量的数学期望可以给出如下定义:
定义4.1.2 设连续型随机变量X的密度函数为f(x)。若,则称积分
为X的数学期望,记为E(X),即
若 ,则称随机变
量X(等价地,相应的分布)的数学期望不存在。
例4.1.2 (泊松分布的数学期望)设随机变量X服从泊松分布
π(λ)(λ>0),则
这表明泊松分布中的参数λ恰好就是此分布的数学期望。那么若已
知泊松分布的期望,则该泊松分布就完全确定了。
例4.1.3 (指数分布的数学期望)设随机变量X服从指数分布
E(λ)(λ>0),则
即指数分布的数学期望为其参数λ的倒数,这也说明指数分布可由其数
学期望完全确定。例4.1.4 (标准正态分布的数学期望)设随机变量X服从标准正态
分布N(0,1),注意到标准正态分布的密度函数
是一偶函数,那么xφ(x)是一奇函数,故
一些重要的随机变量的特征数在书后附表1中能查到。
例4.1.5 某厂生产的电子产品,其寿命(单位:年)服从指数分
布,概率密度函数为
若每件产品的生产成本为350元,出售价格为500元。厂方向顾客承诺,如果售出1年之内发生故障,则免费调换一件,之后厂方不再承担后续
责任;如果在1年以上3年之内发生故障,则予以一次免费维修,维修成
本为50元,超过三年,则不负责维修。在这样的体系下,请问该厂每售
出一件产品,其平均净收入为多少?
解 记某件产品寿命为X,售出该产品的净收入为Y,则显然Y是X
的函数,由于X服从指数分布,那么因此售出一件产品的平均净收入为
例4.1.6 从区间[0,1]中随机地抽取n个数,记为Xi
,i=1,2,…,n,n≥1,记
,求E(M)与E(N)。
解 由题意知,Xi
,i=1,2,…,n是相互独立的随机变量,且均
服从U(0,1),其分布函数为
从而M的分布函数为那么M的概率密度函数为
而N的分布函数为
所以N的概率密度函数为
其中
为Beta函数,a>0,b>0。
关于随机变量期望的计算问题,还有以下定理。
定理4.1.1 若随机变量X的分布函数为F(x),则特别地,当X为非负随机变量(即P(X≥0)=1)时,有
当X为取非负整数值的随机变量时,有
证明略,因为证明需要用到带有斯蒂尔切斯积分的一般随机变量数
学期望的定义。
例4.1.7 设X服从(-1,2)上的均勾分布。令Y=max{X,0},求E(Y)。
解 由Y的定义知其分布函数为
可见,Y既不是离散量,也不是连续量。由于P{Y≥0}=1,利用
(4.1.4)式,可得
例4.1.8 设随机变量X的分布律为
是发散的,故该分布的数学期望不存在。下文中,如无特殊说明,总是假设所提到的随机变量的数学期望是
存在的。
(二)随机变量函数的数学期望
有时会碰到这样的情形:已知随机变量Y=g(X),其中随机变量
X的分布已知,需要得到Y的数学期望。一种自然的思路是先利用两者之
间的关系式及X的分布来求出Y的分布,然后再根据数学期望的定义来得
到Y的期望。这样当然是可行的,但是期望仅仅是随机变量的一个数字
特征,也就是一局部信息。为了得到部分信息,而要先得到其全部信
息,似乎有点“小题大作”之嫌。事实上,当两者之间的函数关系满足一
定条件时,确实不用这么麻烦。可以根据两个变量的关系表达式及已知
随机变量的分布,直接来求另一个随机变量的期望。下面就给出这一简
便公式。
定理4.1.2 当X为离散型随机变量时,若
,则g(X)的数学期
望E(g(X))存在,且
其中P(X=xi)=pi
,i=1,2,…为X的分布律。
当X为连续型随机变量时,若
,则g(X)的数学期望E(g(X))存在,且
其中f(x)为X的概率密度函数。证明 我们仅就X为离散型随机变量时给出证明。类似可证明连续
型随机变量情形。
记Y=g(X),由离散量取值的至多可列的性质可知,Y仍然是离
散量,其可能取值记为y1
,y2
,…,则
由假设知
所以E(Y)=E(g(X))存在,且
即为(4.1.6)式。
上述定理还可以推广到两个或两个以上随机变量函数的情形。
定理4.1.3 当(X,Y)为二元离散型随机变量时,若实函数h(x,y)满足
则h(X,Y)的数学期望E(h(X,Y))存在,且其中
的联合分布律。
当(X,Y)为二元连续型随机变量时,若实函数h(x,y)满足
则h(X,Y)的数学期望E(X,Y))存在,且
其中f(x,y)为(X,Y)的联合密度函数。
例4.1.9 某校区的门口设有电瓶校园游览车,每天早上7:00开始发
车,每隔15分钟一班。假设某人在早上9:00~10:00之间随机来到校门口
乘坐游览车,求此人等候游览车的平均时间。
解 由题意,设该游客在9点的第X分钟到达校门口乘坐游览车,则X服从[0,60]上的均匀分布。用Y表示该游客的等候时间,则根据游
览车的发车安排,有
所以例4.1.10 对于例4.1.7中的Y=max{X,0}的期望,也可以用随机
变量函数的期望来求。
解 由于X的密度函数为
取g(x)=max{x,0},则Y=g(X),利用(4.1.7)式,可得
例4.1.11 随机变量X,Y相互独立,均服从参数为 的0-1分
布,求:
解 由题意知,X与Y的联合分布律为
利用(4.1.8),可得同理可得
例4.1.12 设二元随机变量(X,Y)的联合概率密度为
求E(XY)。
解 利用定理4.1.3,可知
在数学期望的实际应用中,还常常涉及到极值的求解。
例4.1.13 设按季节出售的某种应时产品的销售量X(单位:吨)是
一个服从[5,10]上均匀分布的随机变量。若销售出一吨产品可盈利2
万元;但若在销售季节未能售完,造成积压,则每吨产品将会净亏损
0.5万元。若该厂家需要提前生产该种产品,为使厂家能获得最大的期
望利润,问:应在该季生产多少吨产品最为合适?
解 设该季应生产a吨产品(5≤a≤10),利润为Y万元,则Y依赖于销售量X及产量a,由于X服从[5,10]上的均匀分布,所以其概率密度函数为
所以该季平均利润为
为求使得该季平均利润达到最大的a,令
,所以当a=9时,E(Y)达到最大
值,即从能获得最大的期望利润角度出发,厂家应在该季生产9吨产品
最为合适。
(三)数学期望的性质
定理4.1.4 若n个随机变量,X1
,X2
,…,Xn
的期望都存在,则对任
意n+1个实数 ,的期望也存在,且
当n=l和n=2时可用定理4.1.2和4.1.3来证明,然后利用归纳法易得
上述结论。这里就不详细证明了。
特别地,当ci
=0,i=l,2,…,n时,得E(c0)=c0
,即对于任意
常数c,有
例4.1.14 (正态分布的数学期望)随机变量X服从正态分布
,所以任意正态分布的随机变量都可以写成标准正态分布随机变量的线
性组合,即X=σ·Z+μ,据例4.1.4知E(Z)=0,那么
这表明正态分布中的参数μ恰是此分布的数学期望。
例4.1.15 计算机程序随机地产生0~9中的数字。记Xi
为第i次产生的
数字,i=1,2,…,n。将这n个数依次排列(第一个产生的数字放在
个位,第二个产生的数字放在十位,…,依此类推),得到一数,记
为Y,求E(Y)。
解 由题意知,Xi
独立同分布i=l,2,…,n,其分布律均为故对任意的
,从而
例4.1.16 一民航机场大巴载有20位乘客从机场开出,沿途有10个
车站可以下车,如到达一个车站没有乘客下车就不停车,以X表示沿途
停车的次数,求该大巴平均停车次数(假设每位乘客下车与否是相互独
立的,并且在每个车站下车是等可能的)。
解 令
则显然 的分布律为
此题中将一个复杂的随机变量分解为若干个分布简单的易求数学期
望的随机变量之和,再利用期望的线性组合的性质使得问题迎刃而解。
这种处理方法具有一定的代表性。
例4.1.17 (二项分布的数学期望)设随机变量X服从二项分
布B(n,p)(0
独立且具有相同参数的0-1分布随机变量的和,即令Yi
表示服从参数同
为p的0-1分布的相互独立的随机变量,i=l,2,…,n,则
于是。
当然此结果也可以采用数学期望的定义得到(读者不妨自己计算一
下)。
注意:例4.1.16中的Xi
虽然服从参数相同的0-1分布,但是它们之
间不是相互独立的,因此 不服从二项分布。这一点请读者细
细体会,在以后的实际应用中要特别留意,加以区别。但是由定理
4.1.4,可知随机变量之和的期望是不依赖于和项中随机变量之间的关系
的。
例4.1.18 设有m个0与n个1随机地排成一个序列,m≥1,n≥1,假设
每种排列都是等可能的。在排列中,以0为界限的一串1或以1为界限的
一串0,称之为一个游程,即,连在一起的一串0构成“0”的一个游程,连在一起的一串1构成“1”的一个游程。例如,m=5,n=4,形成这样一
个排列:0,0,0,1,1,0,1,1,0,则这个序列中有3个“0”的游程
和2个“1”的游程。记R(i)为排列中“i”的游程的个数(i=0,1),求
各类游程的平均个数。
解 易知这样的?m+n个数的排列一共有(m+n)!(m!n!)种。令
那么 ,由于
当2≤i≤m+n时,所以
类似可得, 。这样序
列的总游程的均值为
定理4.1.5 n个相互独立随机变量的乘积的期望等于它们期望的乘
积。即若随机变量X1
,X2
,…,Xn
相互独立,期望都存在,则的期望也存在,且
证明 下面仅就n=2且(X1
,X2)是连续型的情形给出证明,其他
情形可以类似得到。设(X1
,X2)的联合密度函数是f(x,y),其边际
密度函数为fi
(x),i=1,2。由独立性,知f(x,y)=f1
(x)
·f2
(y)。此时利用定理4.1.3,有
故X1
X2
的期望存在,且再次利用定理4.1.3,有
例4.1.19 一长方形土地,其边长的测量值(单位:米)X,Y分别
服从N(150,32)和N(165,22),且X与Y相互独立,求土地面积W的
数学期望。
解 由题意知,W=XY,且X与Y相互独立,故
(四)条件数学期望
在§3.1、§3.2与§3.3中曾涉及到离散型和连续型随机变量的条件分
布,我们知道条件分布也是一种概率分布,因此也可以关于它求数学期
望,称为条件数学期望(conditional expenctation),简称为条件期
望,其具体定义如下:定义4.1.3 若(X,Y)为二维离散型随机变量,且在给定X=x
下,Y的条件分布律为;或者(X,Y)为二维连续型随机变量,在给定{X=x}下,Y的条件
概率密度函数为 ,则在给定了随机变量X取值
为x的条件下,Y的条件期望为
有时也简记为E(Y|x)。
期望所具有的性质,条件期望也同样满足。不过值得注意的是,条
件期望与期望还是有一些区别的。期望E(Y)是一个数值,而条件期
望E(Y|X=x)是x的函数。因此E(Y|X)是个随机变量,当观测到X
=x,时,其值为E(Y|X=x)。对于随机变量E(Y|X),还有以下
一个有趣的性质:
定理4.1.6 (X,Y)为二维随机变量,若存在,则
上式称为全(数学)期望公式(total expectation formula)。
特别地,当(X,Y)为二维离散型随机变量时,(4.1.13)就变成
了
其中xi
,i=l,2,…,为X的所有可能取值。
证明 我们就连续型随机变量与离散型随机变量分别进行证明。先
设(X,Y)为二维连续型随机变量,若其联合概率密度函数为f(x,y),记X与Y的边际概率密度函数分别为fX
(x)与fY
(y)。由条件期望定义知
其中 是在{X=x}条件
下Y的条件密度函数。由此可知E(Y|X)是X的函数,那么利用随机变
量函数的数学期望计算公式(4.1.7),得
若(X,Y)为二维离散型随机变量,若其联合分布律为pij
=P{X
=xi
,Y=yj
}(i,j=1,2,…)。同样利用条件期望的定义,(4.1.6)式以及条件概率定义,得
例4.1.20 设进入某超市的顾客购买一件该超市的自创品的概率
为p(0
泊松分布,求一天中该超市卖出其自创品的平均件数。
解 设一天中该超市卖出其自创品的数目为N件。由题意知,当顾
客流量X=i时,N的条件分布为B(i,p),因此对任意的i=0,l,…,有E(N|X=i)=ip。利用全期望公式,可得此题也可以参照例3.1.4,先求出N的分布律,可以得到N服从参数
为pλ的泊松分布,从而得E(N)=pλ。
例4.1.21 在某游戏迷宫的入口处,有编号为1,2,3,4的四个
门,每位游客可先从装有编号为1,2,3,4的4个号码中(等可能地)
随机取一号码,作为进入的门号,4个门中其中有一个是自由门(没有
固定的编号),选择此门,则5分钟后可以走出迷宫;剩下的三门分别
在走了10分,20分,30分钟后又重回人口处。重复前面的步骤,求他走
出迷宫所需的平均时间。
解 设游客走出迷宫所需时间为T分钟,并设他对门的选择情况
为X,用1,2,3,4分别表示自由之门及走了10分,20分,30分钟后重
回入口处的门号,那么
且
其中T1
为选择非自由之门返回入口处后到走出迷宫所需的时间。由题意
知,此时间的概率分布应该和T的分布是一样的,因此
利用全数学期望公式(4.1.13),得由此可解得,E(T)=65(分钟)。§4.2 方差、变异系数
(一)方差的定义
定义4.2.1 设随机变量X的数学期望存在,若E(X-E(X))2
存
在,则称E(X-E(X))2
为X(等价地,相应的分布)的方差,记
为D(X)Var(X)。其中D是英文deviation的第一个字母,Var是
variance的前三个字母(有时也可为V(X))。
从方差的定义可知,它反映了随机变量X的取值与其中心位置——
数学期望的平均偏离程度。这一特征当然也可以用变量对其平均值的绝
对偏离的平均值E|X-E(X)|来衡量,但由于在数学上绝对值的运
算不甚方便,因此改用具有同样效果而又便于运算的方差来代替。
方差的平方根 称为随机变量X的标准差或均方
差,记为SD(X),其中SD是英文standard deviation的縮写。它与方差
一样反映了随机变量与其中心位置的偏离程度。其优点是:它与随机变
量和数学期望具有相同的量纲。
按方差的定义可知,方差的计算可以看成随机变量的函数g(X)=
(X-E(X))2
的数学期望。值得注意的是函数表达式中的E(X)是
一实数。那么根据定理4.1.2可知:
(1)若离散型随机变量X的分布律为P(X=xi)=pi
,i=1,2,…,则X的方差为
(2)若连续型随机变量X的密度函数为f(x),则X的方差为
直接按定义计算方差往往比较麻烦,人们常常用下面的公式来计算
方差。定理4.2.1 若随机变量X的方差存在,则
证明 利用方差的定义及定理4.1.4,得
由上面的定理,显然可得
由于上式中的各项都是非负项,所以若E(X2)<+∞,可得D(X)<+
∞。其实反之也成立,即若D(X)<+∞,也可得出E(X2)<+∞。另
外,由于|X|?X2
+1,所以某一随机变量的方差若存在,则一定保证
了其数学期望的存在性。
例4.2.1 (泊松分布的方差)设随机变量X服从泊松分布π(λ)
(λ>0),则
又E(X)=λ,故D(X)=λ2
+λ-λ2
=λ。这表明泊松分布的数学期望与
方差都等于参数λ。
例4.2.2 (指数分布的方差)设随机变量X服从指数分布E(λ)
(λ>0),则
而即,指数分布的方差为其数学期望的平方。
例4.2.3 (标准正态分布的方差)设随机变量X服从标准正态分
布N(0,1),而
故D(X)=1-02
=1。
例4.2.4 对于例4.1.6中的M与N,分别求出其方差。
解 由M与N的密度函数,可得
(二)方差的性质
定理4.2.2 设随机变量X的方差存在,c为某一常数,则
(1)D(cX)=c2
D(X);
(2)D(X+c)=D(X);
(3)D(X)?E((X-c)2),其中当且仅当E(X)=c时等号成
立。
证明 按方差定义及上一节中提及的数学期望的线性性质,知(1)得证。同样利用方差定义,且上式当且仅当E(X)=c时等号成立,故得结论(3)。
一个常数c可以看成一个特殊的随机变量,其数学期望E(c)也
是c,因此这一特殊随机变量与其中心位置的偏差为0,即其方差为0;
反之,某随机变量X的方差为0,可见其取值非常集中,均集中在某一
点,此点即为其中心——数学期望。于是有下面的这一性质:
定理4.2.3 设随机变量X的方差存在,则D(X)=0当且仅当P(X
=c)=l,其中c=E(X)。
证明 若P(X=c)=1,其中c=E(X),那么根据方差的定义可
得D(X)=0,即定理的充分性得证。而定理的必要性证明需要用到切
比雪夫不等式,此不等式我们将在第五章中介绍,所以这一部分的证明
可以参见例5.1.2。
定理4.2.4 对任意的正整数n?2,设X1
,X2
,…,Xn
为两两独立的随
机变量,方差都存在。则X1
+X2
+…+Xn
的方差也存在,且
证明 注意到由于对任意的1?i
与Xj
两两独立,故由定理4.1.5知,故对任意i≠j,有
另外,结合定理4.2.2中的(1)可得:
推论4.2.1 对任意的正整数n?2,设X1
,X2
,…,Xn
为两两独立的随
机变量,方差都存在。则对任意的有限实数
的方差也存
在,且
例4.2.5 (二项分布的方差)设随机变量X服从二项分布B(n,p)(0
个相互独立且具有相同参数p的0-1分布随机变量的和,即令Yi
表示服从
参数同为p的0-1分布的相互独立的随机变量i=1,2,…,n,则
,于是
例4.2.6 (正态分布的方差)设随机变量X服从正态分布,据例4.2.3,知D(Z)=1,那么利用定理4.2.2,有
这表明正态分布中的参数σ2
表示的是此分布的方差,结合例4.1.14的
结果,我们知正态分布由其数学期望与方差完全确定。故常称为“期望
为μ,方差为σ2
(或标准差为σ)的正态分布”。而方差越小,正态分布的
取值就越集中在均值μ的附近。
(三)标准化变量与变异系数
定义4.2.2 若随机变量X的方差存在,那么称
为X的标准化随机变量。显然E(X)=0,D(X)=1,而且此类变
量是无量纲的。
事实上,引入标准化随机变量主要是为了消除由于计量单位的不同
而给随机变量带来的一些影响。例如:进行精密测量时,对于某物长度
的考察当然可以用厘米作为单位,得到随机变量X,也可以用毫米作为
单位,得到随机变量Y。那么Y=10X,从而X与Y的分布有所不同。这显
然不太合理。但通过标准化变换,就可以消除这种不合理性。之前常用
的标准正态变量也是一般正态变量经标准化变换得到的。
类似地,度量分布离散性的数字特征——方差也会由于这种量纲上
的不同而不同,如上例中,若X的方差为σ2
,那么Y的方差为100σ2
,若以
此认为Y较之X更为分散,显然是不合理的。为了消除量纲及取值大小
(包含单位不同)的影响,常用无量纲的来作为衡量指标,称之为变异系数(或称为标准离差率或单位风险,在
工程上,有时也称为变差系数),其中Cv是coefficient of variation的简
写。它反映了随机变量X在以它的中心位置为标准时,取值的离散程
度。那么,前一段落中提到的X与Y的变异系数显然是相同的,这也与实
际情况相符。
例4.2.7 已知甲乙两地居民的月收入分别服从N(1500,1502)
与N(2800,2202)(单位:元),试比较这两个地区贫富差异的程
度。
解 由题意知甲、乙两地居民月收入的方差分别为1502
,2202
,即
从方差的角度看甲地居民的贫富差异比乙地小。但也有人注意到了甲地
平均收入为1500,乙地的平均收入为2800相差较大,应该用变异系数来
反映两地区的贫富差异性较合适。两地的变异系数分别为
因此从变异系数角度看甲地居民的月收入的离散程度高于乙地,即甲地
居民的贫富差异比乙地大。
相比较方差(或标准差)而言,变异系数在比较两组量纲不同或均
值不同的变量时更能体现其优点。因此变异系数在概率论的许多分支中
都有应用,如:更新理论、排队理论、可靠性理论,等等。但是它也有
其缺陷,从它定义可知,如果一个随机变量的均值为0,那么此变量的
变异系数就没有意义。事实上,当变量的均值接近于0的时候,均值的
一点小小的变动也会对变异系数产生巨大影响,因此容易造成精确度上
的不足。§4.3 协方差与相关系数
对于多元随机变量,除了考虑每一个分量的中心位置和离散程度,借此来了解各个分量各自的部分特性外,还对于它们之间的关系感兴
趣。本节中我们将介绍反映两个变量间线性关系的两个数字特征——协
方差与相关系数。
(一)协方差
回想期望的性质之一——定理4.1.5,对于相互独立的随机变量X和
Y,当其期望都存在时,有E(XY)=E(X)E(Y),而此式等价于
那么当E{(X-E(X))(Y-E(Y))}≠0时,则X和Y一定不独
立,也就是存在某种相依关系,因此我们认为E{(X-E(X))(Y
-E(Y))}可以在一定程度上反映出X和Y的某种关系,对此给出下
面定义。
定义4.3.1 对于期望都存在的随机变量X和Y,当(X-E(X))
(Y-E(Y))的期望存在时,称
为X与Y的协方差,其中Cov是英文covariance的前三个字母。
按协方差的定义可知,协方差的计算可以看成二元随机变量的函数
的数学期望,那么根据定理4.1.3可知:
(1)若二元离散型随机变量(X,Y)的联合分布律为P(X=xi
,Y
=yj)=pij
,i=l,2,…,j=1,2,…,则X与Y的协方差为(2)若二元连续型随机变量(X,Y)的联合密度函数为f(x,y),则X与Y的协方差为
直接按定义计算协方差往往比较麻烦,在实际应用中常常用下面给
......
您现在查看是摘要介绍页, 详见以上附件 。